基于S变换和时频谱空间滤波的超声缺陷回波检测方法

曾 祥， 吴学雷， 周晓军， 杨辰龙， 陈越超

(1. 浙江大学 流体动力与机电系统国家重点实验室，杭州 310027; 2. 北京航天发射技术研究所，北京 100076)

基于S变换和时频谱空间滤波的超声缺陷回波检测方法

曾 祥1， 吴学雷2， 周晓军1， 杨辰龙1， 陈越超1

(1. 浙江大学 流体动力与机电系统国家重点实验室，杭州 310027; 2. 北京航天发射技术研究所，北京 100076)

缺陷回波的检测是超声探伤的一项重要内容，为减弱噪声的影响准确检测缺陷回波，提出基于S变换时频分析和时频谱空间滤波的信号处理方法。讨论了高斯回波模型下的到达时间和中心频率与S变换时频谱的关系，说明了利用S变换时频谱幅值矩阵的极值提取回波到达时间和中心频率的合理性；为检测回波，首先对原始信号作S变换，然后对得到的时频谱幅值矩阵应用最大熵法自适应选择去噪阈值，对S变换时频谱作空间滤波完成降噪；从降噪后的区域中提取反映缺陷的到达时间和中心频率；对降噪后的时频谱作S逆变换，获得缺陷回波明显的时域信号。仿真研究表明，基于S变换和时频谱空间滤波的方法能够有效去除噪声，检测回波。棒材试块的实验结果同样表明了该方法在缺陷检测上的有效性。

超声；S变换；最大熵阈值；空间滤波

超声脉冲反射法是一种重要的无损检测方法。缺陷回波提供了材料内部的缺陷信息，到达时间(Time of Arrival, TOA)和中心频率(Center Freguency, CF)是反映回波的两个重要参数。由于噪声的存在，缺陷回波在时域上容易被掩盖，在时频域上噪声容易形成多个峰值。为此，国内外学者对含噪超声信号中的缺陷回波检测进行了研究[1]，采用了小波变换[2]、自适应滤波[3]、经验模态分解[4]、盲源分离[5]等方法。

本文提出一种基于广义S变换时频分析和最大熵阈值分割算法的超声缺陷回波检测方法。首先对回波信号作广义S变换，获得时频谱系数矩阵；然后对时频谱系数矩阵作空间滤波降噪，基于最大熵法确定双阈值并处理；最后从降噪后的时频谱系数矩阵中提取回波参数，作S逆变换得到降噪后的缺陷回波信号。

1 基于S变换的回波参数提取

1.1 广义S变换

S变换是短时傅里叶变换和小波变换的继承和发展，由Stockwell等[6]在研究地球物理数据时提出。相比短时傅里叶变换，S变换具有多分辨率特性，即在信号低频段具有高的频域分辨率，在信号高频段具有高的时间分辨率。相比连续小波变换，S变换保持了原始信号的相位信息。因此，S变换被广泛应用于心电信号(Electrocardiogram, ECG)[7]和心音信号处理[8]、滚动轴承故障信号分析[9]、地震波分析[10]等领域。

(1)

当p=1时，即为S变换。当plt;1时，相对S变换窗宽变宽，时间分辨率下降，频率分辨率上升；pgt;1时相反。调节因子p，可以实现时频分辨率的灵活调整、能量优化集中。为描述简便，不论p取值，统称为S变换。

1.2 回波参数提取原理

单个高斯回波为

s0(τ)=βe-α(τ-b)2cos[2πfc(τ-b)+φ]

(2)

用复数表示为

s0(τ)=βe-α(τ-b)2ej[2πfc(τ-b)+φ]

(3)

信号能量Es0为

(4)

式中：β为信号强度；α为带宽因子；b为到达时间；fc为中心频率；φ为初相位。回波为窄带信号，99%以上的能量集中在非指数项，满足f2c≥0.24α[12]。

对s0(τ)作S变换，得到幅值矩阵元素

(5)

其中,

(6)

(7)

(8)

一般认为，回波的到达时间b和中心频率fc可以通过求|S(t,f)|的极值位置提取。令∂|S(t,f)|/∂t=0，有

(9)

t=b与回波的其他参数和S变换的窗宽因子p无关。因此，S变换非常适合对超声回波信号的TOA提取。

(10)

容易验证t=b，f=fc时A+B=0且∂(A+B)/∂f= 0，有

(11)

可见当t=b，f=fc时，若p=0(Gabor变换)，∂W/∂f=0，极值点坐标满足f=fc，与现有结论一致[13]。若pgt;0，有∂W/∂fgt;0，可以推测极值点坐标fgt;fc。因此|S(t,f)|取极值时的频率高于信号的实际CF。尽管S变换对CF的提取有偏移，但它的多分辨率分析能力使得它在实际信号分析中应用广泛。

为定量分析频率的偏移量与其他参数的依赖关系，令∂W/∂f=0，并将t=b代入，可以得到

pqw2+πf(α+q)w+pα(α+q)/2=0

(12)

式中：w=π(fc-f)=πΔf；q=f2p/2。求解得到

(13)

Δf为α、f、p的函数且Δflt;0，如图1(a)。从上到下的4个曲面依次对应p=0.25、p=0.5、p=0.75和p=1。图1(b)为p=1时情形，从左到右10条实线依次对应f为1 MHz, 2 MHz, …, 10 MHz的Δf(虚线表示不满足f2c≥0.24α条件)。

(a) Δf随α、f、p的值

(b) p=1时的Δf随α、f的值图1 CF偏差分析Fig.1 Bias analysis of CF

偏差Δf的变化趋势为随p的增大和α的增大而增大，随f增大而减小。当p、f均确定时，Δf随α近似成正比例下降。

可见由极值条件得到的f是CF的近似值。取最大相对误差ef=Δf/(f-Δf)×100%，由图1(b)可知，p=1时ef约为15%。实际中高频回波由于α有限，ef将降低。如α∈[0,80]，f为10 MHz的最大偏差约为0.4 MHz，ef=-0.4/(10-0.4)×100%=-4.2%。因此以f近似地作为CF能够满足实际检测要求。如果需要CF的精确值，可以考虑Gabor变换，求解优化问题得到TOA、CF，精度较高，但需要额外计算；减小p可实现增大频率分辨率、降低Δf和ef，但时间分辨率将下降。

若对S变换的窗函数作能量归一化，此时需在式(5)的前面乘以能量归一化因子η

(14)

同样可以得到极值条件下TOA没有偏差，CF存在偏差

(15)

两种情形下Δf相差很小。读者可自行分析，与图1(b)对比。

考虑实际检测中，本文不作能量归一化，直接按极值条件确定TOA、CF，且p=1。值得注意的是，本文忽略了实际信号由于采样频率、信号长度有限造成的偏差和不同p值下时频分辨率不同造成的偏差。

2 时频谱空间滤波

2.1 问题转换

对x(t)作S变换，得到的时频谱系数矩阵S是复数矩阵，它的幅值矩阵反映了信号能量在不同时间段、频率段的分布情况，可以视作一帧像素灰度值可为任意非负值的灰度图像I，可以采用数字图像的空间滤波方法进行处理。这样，由于时频图的“可视化”效果，相比小波阈值去噪和模极大值去噪，过程逐步直观。

阈值法是常用的降噪方法，通过选择合理的阈值T，将S分成回波时频谱和噪声时频谱两部分。该过程相当于对灰度图像I用阈值T作分割，结果为I与J的乘积，其中J为乘积模板，满足

(16)

若J(i,j)=1，则称为前景；反之为背景。初始时J为零矩阵。采用单阈值时，在阈值附近的值处于“模糊”状态，为保留较多信息采用双阈值。设阈值TH、TL(THgt;TL)，分别得到JH、JL。JH中的前景属于回波，JL的背景全为噪声，而JH的背景和JL的前景的交集C可以利用灰度在像素空间的分布信息判定。将C中的所有判定得到的前景点加入到JH即为J。强噪声下J中可能出现小面积前景，属于伪回波区域，需要去除。

将时频谱系数矩阵S与J逐点相乘，即可得到降噪后的时频谱系数矩阵Sn。

2.2 双阈值选择

灰度图像的自适应全局阈值分割算法有大津法(OTSU)[14]、最大熵法等，其中最大熵法对不同信噪比的图像均能产生较好的分割效果。本文采用最大Kapur熵法[15]确定分割阈值。

设灰度图像I有L个灰度级，阈值T将其分割为背景A和前景B两部分。A区域像素的灰度值k1,k2, …,km均不高于T，B区域像素的灰度值km+1,km+2,…,kL均高于T。再记I的总像素数为N，第i个灰度级的像素数为Ni。那么A、B区域像素灰度的概率分布为

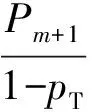
式中：pi=Ni/N为第i个灰度级的概率，而

A、B部分的熵计算为

(18)

总的熵H为

H=H(A)+H(B)

(19)

H取得最大值意味着获取的前景区域A和背景区域B的总信息量最大，对应的阈值即为最佳全局阈值。将此阈值作为高阈值TH。

认为I中小于TH的其他元素基本由噪声形成，计算它们的均值TM，将低阈值TL取作TH和TM的均值，即TL=(TH+TM)/2。

由此TH、TL均被自适应确定。应用TH、TL对I按式(16)进行二值化分别得到JH、JL。

2.3 交集处理和伪回波区域去除

对C中像素，若为回波，应该“环绕”着JH的前景且距离不能过远。对JH作距离变换，计算各点到最近前景点的最短欧氏距离，结果记为DJH。给定最大允许距离D≥ 0，任意像素C(i,j)，若满足DJH(i,j)lt;D，则认为对应回波取作前景，即令JH(i,j)=1；反之则认为对应噪声。显然，D=0时C中的点均被认为是噪声，相当于用高阈值TH进行单一阈值去噪；D足够大时，C中的点均被认为是回波，相当于用低阈值TL进行单一阈值去噪。

若JH存在伪回波小区域，可给定系数κ，对所有N个区域面积从大到小排序，记A(n)为区域n的面积，记面积比qn=A(n)/A(n-1)，若qm≤κ均成立(n=N,N-1,…,2;m=n,n+1,…,N)，则将区域n设为背景。或者经过有限次腐蚀后再做有限次膨胀。实际中小区域面积和回波区域往往相差明显，可以直接指定系数κ，本文采用这种方法。最终得到的二值矩阵即为乘积模板J。

3 基于S变换和时频谱空间滤波的回波检测

从受到噪声干扰的信号x(τ)中检测缺陷回波的步骤如下：

步骤1 S变换。对x(τ)作S变换得到时频谱系数矩阵S，由S计算谱系数幅值得到幅值矩阵I。记I中元素的最小值、最大值分别为u、v。

步骤2 低通滤波和双阈值选择。估计回波的上限频率fu，取I中频率低于fu的区域作为感兴趣区域(Region of Interest, ROI)。选择迭代步长Δ，计算阈值为T0=u+ (i-1)Δ时的熵Vi，其中正整数i为计算次数。递增i直到T0≥v结束迭代。得到阈值序列{T0}和对应的熵序列{H}。

步骤3 阈值化。计算双阈值TH、TL，根据TH、TL对I执行阈值化，得到JH、JL；处理交集C，选择D将C

中距离小于D的区域加入JH的前景；如有必要，指定系数κ，去除JH的小区域。最终得到乘积模板J。

步骤4 空间滤波。将时频谱系数矩阵S与J逐点相乘，得到降噪后的时频谱系数矩阵Sn。

步骤5 回波参数提取和信号重建。从Sn中提取TOA、CF。对Sn作S逆变换，得到降噪后的信号x1(τ)。

4 仿真研究

为验证提出的超声缺陷回波检测算法的有效性，构造仿真信号x(t)进行研究。设具有K重回波的超声信号x(t) =s1(t) +…+sK(t)+n(t)。n(t)为零均值，方差为σ2的高斯白噪声。记E0为回波信号的能量，信噪比SNR单位dB，SNR=10lg(E0/σ2)。

考虑到本文方法φ对回波检测没有影响，所以仿真中忽略φ。对单个缺陷回波si(t)，设λi=[βiαibifci]T，取K=4，λ1=[1 15 3 7.5]T，λ2=[0.95 15 4 6.5]T，λ3=[0.90 12 6 5.5]T，λ4=[0.90 10 8 4.5]T构造s(t)，并向s(t)中添加SNR=-2 dB的噪声信号n(t)，获得含噪信号x(t)。仿真信号采样频率fs=50 MHz，选择低通滤波频率为20 MHz。

图2 仿真信号处理结果Fig.2 Processing result of simulation signal

可见对低信噪比混合信号x(t)(见图2(b))，S变换后缺陷回波信号明显(见图2(c))。经双阈值THTL处理和交集处理和去除伪回波小区域后得到乘积模板J(见图2(d))。J与S逐点相乘得到降噪后的时频谱Sn(见图2(e))，经S逆变换后重建时域波形(见图2(f))。可见，重建的信号波形完备清晰。基于Stein无偏似然估计和极大极小方法选择的阈值将部分噪声信号误认为缺陷回波信号予以了保留；而固定阈值的降噪方法去除了较多有效信息，得到的缺陷回波近似呈现脉冲状(见图2(g))。另外，由于本文方法仅保留了信号能量较高的时间频率段成分，因此降噪后的信号幅值降低；但对于强噪声下的缺陷检测和定位并无影响。可以预见，弱噪声下，由于阈值的降低，降噪后的信号幅值降低较小。

为定量评价本文回波特征提取方法的有效性，对原始信号和处理后的信噪比(Signal-to-Noise Ratio, SNR)、均方根误差(Root-Mean-Square-Error, RMSE)列入表1。TOA、CF的提取结果列入表2。

表1 信噪比和均方差

表2 参数提取结果

由表1可知，相比给出的3种小波阈值去噪方法，本文方法的信噪比提升明显，均方差较小。其他3种方法，采用固定阈值和极大极小阈值的信噪比较高，均方差较小。由表2可知，经S变换可以方便地获取回波信号的TOA和CF，且偏差较小。偏差的来源主要有3方面，包括时频分辨率的限制、噪声与回波在时频域上的混叠，以及S变换极值处频率对CF的偏移。但总体而言，在混叠较小的情形下，TOA和CF的提取偏差较小。

为进一步比较本文方法和3种小波阈值方法在不同SNR下的降噪效果，改变仿真信号中加入噪声的强度，取SNR = 4 dB，2 dB，0 dB，-2 dB，-4 dB。为减弱处理的随机性，对每个SNR重复3次，计算3次处理后的SNR和MSE的平均值作为最终结果，如图3所示。

可见，相比使用的3种小波阈值去噪方法，本文方法去噪的效果更好。因此，数字图像处理技术应用于回波信号去噪是可行的。事实上，本文方法与小波阈值去噪法是相通的，都是在时频域上去除或减弱幅值低于阈值的局部成分。借助于数字图像处理技术，本文方法过程更加直观。

(a) 处理前后的SNR

(b) 处理前后的MSE图3 不同SNR下降噪效果比较Fig. 3 Comparison of denoising effects with different SNR

5 实际回波检测

现在将S变换和时频谱系数矩阵空间滤波方法应用于实际缺陷回波检测。如图4所示，采用20#钢棒材试块，公称直径为Φ120 mm，实测数据为Φ119.94 mm。3个平底孔直径依次为Φ0.8 mm、Φ1.2 mm、Φ2.0 mm作为人工缺陷。本文选取Φ1.2 mm孔作为代表进行检测，其公称尺寸为Φ1.2×埋深90 mm，实测数据为Φ1.22×埋深89.9 mm。材料声速事先已经过测定为c=5 934 m/s。超声探头中心频率为7.5 MHz，信号采样频率为100 MHz。始波和底波之间为背散射信号s(t)，由平底孔缺陷回波s1(t)、结构噪声和微小缺陷散射反射回波s2(t)、噪声n0(t)组成，三者幅度依次减小。现在需检测s1(t)。选择Turkey-Hanning窗函数对s(t)进行截取，截取的采样点区间为1 501～5 000。处理结果如图5所示。

图4 20#棒材试块Fig. 4 20# bar specimen

(a) Turkey-Hanning窗函数

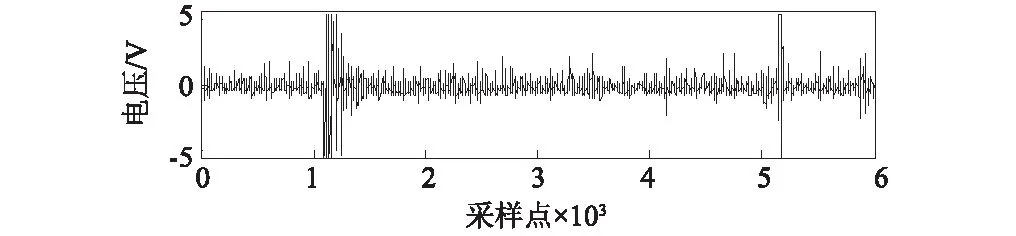
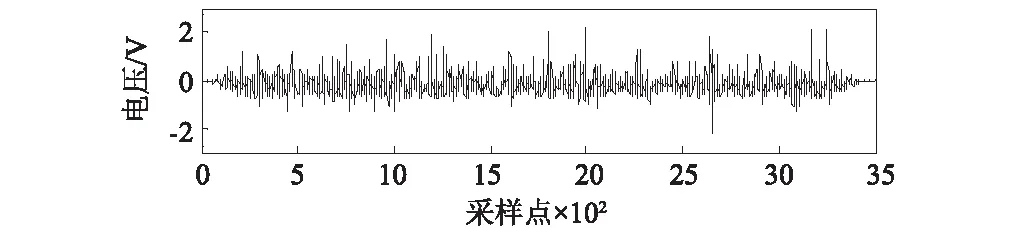
(b) 实测信号和截取后的背散射信号

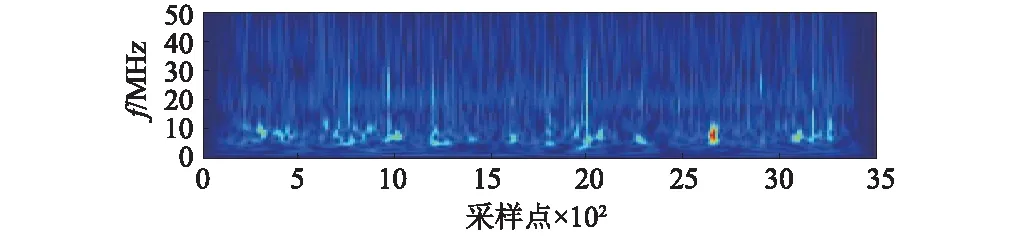
(c) S变换时频图

(d) 还原的信号图5 20#棒材试块人工缺陷回波检测Fig. 5 Echo detection of artificial flaw in 20# bar specimen

从S变换时频图中可以看到明显的缺陷区域(见图5(c))，对应平底孔缺陷，回波在图5(c)的坐标为(2 650, 8.086)。在图5(b)实测信号中时间点为4 201。始波幅值近似达到5V的首末时间点分别为1 107和1 167，取始波位于均值1 137处。计算得到平底孔的位置为：d=cΔt/2=cN/(2fs)=1 000×5 934×(4 201-1 137)/(2×100×106)=90.9 mm，与实测埋深89.9 mm偏差很小，表明TOA的提取是较准确的。还原的信号中缺陷回波更加明显，几乎无噪声，这是因为超声在金属材料中衰减较小，平底孔反射强，从而缺陷回波在时频图上能量集中度很高 (见图5(c))，CF相比探头中心频率上升了约0.5 MHz。

如果需要进一步降噪研究s2(t)，可以用s(t)的S变换时频谱减去s1(t)的S变换时频谱，差值近似作为s2(t)和n0(t)的叠加信号的S变换时频谱(因为s1(t)的检测存在误差)，再进行时频谱系数空间滤波。最终结果如图6所示。

图6 信号成分s2(t)检测Fig. 6 Detection of signal component s2(t)

6 结 论

(1) S变换是一种优秀的时频分析方法，得到的时频谱系数矩阵能够很好地揭示信号的时频特性，可用来提取TOA和CF，适合超声缺陷回波检测。

(2) 基于最大熵法的阈值选择具有自适应、分割优良的优点，能够较好地去除噪声，保留回波信号。

(3) 将数字图像处理技术应用于S变换的时频谱系数矩阵的阈值降噪是有效的，且过程直观可见。可以认为，如短时傅里叶变换、连续小波变换得到的时频图也可以视作灰度图像进行降噪处理。

[ 1 ] ZHANG G M，HARVEY D M．Contemporary ultrasonic signal processing approaches for nondestructive evaluation of multilayered structures[J]．Nondestructive Testing and Evaluation，2012，27(1)：1-27．

[ 2 ] MATZ V，SMID R，STARMAN S，et al．Signal-to-noise ratio enhancement based on wavelet filtering in ultrasonic testing[J]．Ultrasonics，2009，49(8)：752-759．

[ 3 ] 杨克己. 基于神经网络的自适应滤波技术及其在超声检测中的应用[J]．仪器仪表学报，2005，26(8)：813-817．

YANG Keji．An adaptive filter based on artificial neural net and its application in ultrasonic testing[J]．Chinese Journal of Scientific Instrument，2005，26(8)：813-817．

[ 4 ] LU Y F, ORUKLU E, SANIIE J．Chirplet signal and empirical mode decompositions of ultrasonic signals for echo detection and estimation [J]．Journal of Signal and Information Processing，2013，4(2)：149-157．

[ 5 ] LIU Q K，QUE P W，GUO H W，et al．Noise cancellation of ultrasonic NDE signals using blind source separation[J]．Russian Journal of Nondestructive Testing, 2006, 42(1)：

63-68．

[ 6 ] STOCKWELL R G，MANSINHA L，LOWE R P．Localization of the complex spectrum：the S transform[J]．IEEE Transaction on Signal Process，1996，44(4)：998-1001．

[ 7 ] ARI S，DAS M K, CHACKO A．ECG signal enhancement using S-Transform[J]．Computers in Biology and Medicine，2013，43(6)：649-660.

[ 8 ] 李战明，韩阳，韦哲，等. 基于S变换的心音信号特征提取[J]．振动与冲击，2012，31(21)：179-183．

LI Zhanming, HAN Yang, WEI Zhe, et al．Heart sound feature extraction based on S tranformation[J]．Journal of Vibration and Shock，2012，31(21)：179-183．[ 9 ] 郭远晶，魏燕定，周晓军，等. 基于S变换谱阈值去噪的冲击特征提取方法[J].振动与冲击，2014，33(21): 44-50.

GUO Yuanjing, WEI Yanding, ZHOU Xiaojun, et al.An impact feature extracting method based on S transformation spectrum threshold denoising[J].Journal of Vibration and Shock，2014，33(21): 44-50.

[10] 樊剑，吕超，张辉. 基于S变换的地震波时频分析及人工调整[J].振动工程学报，2008，21(4): 381-386.

FAN Jian, LÜ Chao, ZHANG Hui.Time-frequency analysis and artificial simulation of earthquake groud motions via S-transform[J].Journal of Vibration Engineering，2008，21(4): 381-386.

[11] DJUROVIC I, SEJDIC E, JIANG J.Frequency-based window width optimization for S-transform[J].AEU-International Journal of Electronics and Comunications，2008，62(4): 245-250.

[12] DEMIRLI R, SANIIE J.Model-based estimation of ultrasonic echoes Part I: analysis and algrithms[J].IEEE Transaction on Ultrasonics, Ferroelectrics, and Frequency Control, 2001，48(3): 787-802.

[13] LU Z K, YANG C, QIN D H.Estimating the parameters of ultrasonic echo signal in the Gabor transform domain and its resolution analysis[J]. Signal Processing, 2016, 120: 607-619.

[14] OTSU N.A threshold selection method from gray-level histograms[J].IEEE Trans on Systems，Man，and Cybernetics，1979，9(1): 62-66.

[15] KAPUR J N，SAHOO P K，WONG A K C.A new method for gray-level picture thresholding using the entropy of the histogram[J].Computer Vision，Graphics and Image Processing，1985，29(3): 273-285.

AflawechodetectionmethodbasedonS-transformationandtime-frequencyspectrumspatialfiltering

ZENG Xiang1, WU Xuelei2, ZHOU Xiaojun1, YANG Chenlong1, CHEN Yuechao1

(1. The State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China;2. Beijing Institute of Space Launch, Beijing 100076, China)

Detection of flaw echoes is an important task in ultrasonic testing. In order to eliminate the effects of noise and detect echoes correctly, a signal processing method based on the S-transformation (ST) and the time-frequency spectrum (TFS) spatial filtering was proposed．Based on the Gaussian echo model, the relationships between the time of arrival (TOA) together with the center frequency (CF) and ST TFS were discussed. The reasonableness of the method using the extremum of ST TFS amplitude matrix for TOA and CF extraction were illustrated. To detect the echoes, firstly the ST was performed on the original signal．Then the dual-threshold were determined by the Maximum Entropy Thresholding method adaptively, and the spatial filtering was performed on ST TFS for denoising. The TOA and CF could be extracted from the denoised region. Finally, the inverse ST was performed on the denoised TFS and the signal with clear flaw echoes were gained. Simulation results show that using ST and TFS spatial filtering can remove noise and detect echoes effectively. And the experimental results of bar specimen also show the effectiveness of the method in flaw detection.

ultrasonic; S-transformation; maximum entropy thresholding; spatial filtering

浙江省自然科学基金(LY14E050013)；浙江省公益技术研究工业项目(2015C31052)；重庆齿轮箱有限责任公司"海面平台洋流发电装备研制与开发"

2016-03-29 修改稿收到日期： 2016-07-14

曾祥 男，博士生，1989年生

周晓军 男，教授，博士生导师，1958年生

TB553

A

10.13465/j.cnki.jvs.2017.22.006