渗透压下岩石翼形裂纹应力 强度因子及断裂判据
2017-11-28贺泽俞缙张建智蔡燕燕涂兵雄李升才
贺泽, 俞缙, 张建智, 蔡燕燕, 涂兵雄, 李升才
(1. 华侨大学 福建省隧道与城市地下空间工程技术研究中心, 福建 厦门 361021;2. 重庆大学 土木工程学院, 重庆 400044 )

渗透压下岩石翼形裂纹应力强度因子及断裂判据
贺泽1, 俞缙1, 张建智2, 蔡燕燕1, 涂兵雄1, 李升才1
(1. 华侨大学 福建省隧道与城市地下空间工程技术研究中心, 福建 厦门 361021;2. 重庆大学 土木工程学院, 重庆 400044 )
为研究渗透压下岩石翼形裂纹面部分闭合情况下的破坏行为,建立多裂纹间相互作用下压剪翼形裂纹的力学模型,推导得到岩石翼形裂纹尖端应力强度因子表达式.分析不同起裂角条件下,应力强度因子随岩石翼裂纹长度的变化规律,并对参数进行敏感性分析.基于摩尔-库伦准则,推导考虑裂纹间相互作用的部分闭合型裂纹的断裂韧度表达式,得到岩石在压剪应力作用下Ⅰ,Ⅱ型裂纹的复合断裂判据.分析结果表明:裂纹间相互作用对应力强度因子的影响效果显著;应力强度因子在起裂角为65°左右时达到最大;应力强度因子对裂纹起裂角和翼形裂纹长度较敏感,对裂纹闭合度的敏感性较小.
渗透水压力; 岩石; 翼形裂纹; 应力强度因子; 断裂判据
深埋隧洞围岩大多处于压剪受力状态,翼形裂纹是压剪状态下岩石主要的断裂破坏形式,对围岩稳定性影响较大.因此,研究渗透压下翼形裂纹拓展问题意义重大.郭少华等[1]认为渗透压引起的裂纹尖端应力集中是导致张开型翼形裂纹萌生、拓展的重要因素.Li等[2]提出Kachanov计算模型,将其运用到闭合压剪裂纹求解中.张卫东等[3]在摩尔库伦模型的基础上,充分考虑渗透压力的作用,生成考虑初始渗透压力的裂隙岩体本构模型.文献[4-5]对岩石不等长闭合裂纹应力强度因子及起裂规律进行了详尽的研究.文献[6-8]基于不同假定提出了多种闭合翼形裂纹扩展及其尖端应力强度因子的简化计算模型.上述研究均假设翼形裂纹在压剪作用下会完全闭合.但实际上,岩石裂隙在闭合过程中由于受力不均匀,使两个表面不能完全闭合.赵延林[9]研究的翼形裂纹应力强度因子简化计算模型考虑了原生裂隙的不完全闭合及渗透压的作用,但忽略翼形裂纹闭合给应力强度因子带来的影响.为得到渗透压下完整的不完全闭合裂隙应力强度因子,本文提出一个新的压剪翼形裂纹力学模型.再基于摩尔-库伦强度准则,推导渗透压下岩石压剪断裂判据,并对参数进了敏感性分析.
1 翼形裂纹尖端应力强度因子
1.1翼形裂纹面部分闭合
在进行翼形裂纹尖端应力强度因子计算时,王元汉等[6]提出对原生裂纹和翼形裂纹进行叠加计算模型,得到了较好的计算精度,但由于其未考虑裂纹的闭合及渗透水压力等因素,不能反映裂纹部分闭合及多裂纹间相互作用下翼形裂纹尖端应力强度因子的变化情况.考虑到主裂纹及翼型裂纹的部分闭合,引入参数χ表示裂纹的闭合状态[9],其大小由未闭合的裂纹面积与总的裂纹面积的比值确定.由此,渗透水压力的大小变成χp,并以面力的形式作用在主裂纹与翼形裂纹上.翼形裂纹尖端应力强度因子的叠加计算示意图,如图1所示.图1中:σ1和σ3为远场应力;l为翼形裂纹长度;θ为起裂角;2a为主裂纹长度;β为主裂纹与水平向的夹角.翼形裂纹的拓展极其复杂,研究中通常需对其简化.根据断裂力学知识,假定翼形裂纹尖端应力强度因子KI,简化为图1(c)和图1(d)中应力强度因子的叠加,即
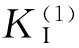

(a) 闭合后 (b) 应力强度因子KI (c) 应力强度因子等效应力强度因子图1 翼形裂纹尖端应力强度因子的叠加计算示意图Fig.1 Superposition diagram of wing cracks intensity factor at tips
主裂纹面上的法向应力σn、切向应力τn及有效剪应力τeff分别为
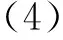
式(4)中:f为裂纹面摩擦系数.
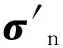
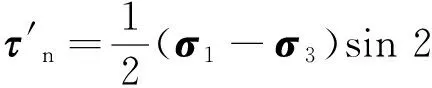
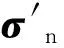
将作用在主裂纹面上的有效剪切应力τeff简化为图1(d)所示,由文献[10]得应力强度因子,即
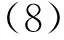
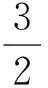
综上,翼形裂纹尖端应力强度因子KⅠ可表达为
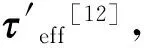

则Ⅱ型裂纹强度因子为
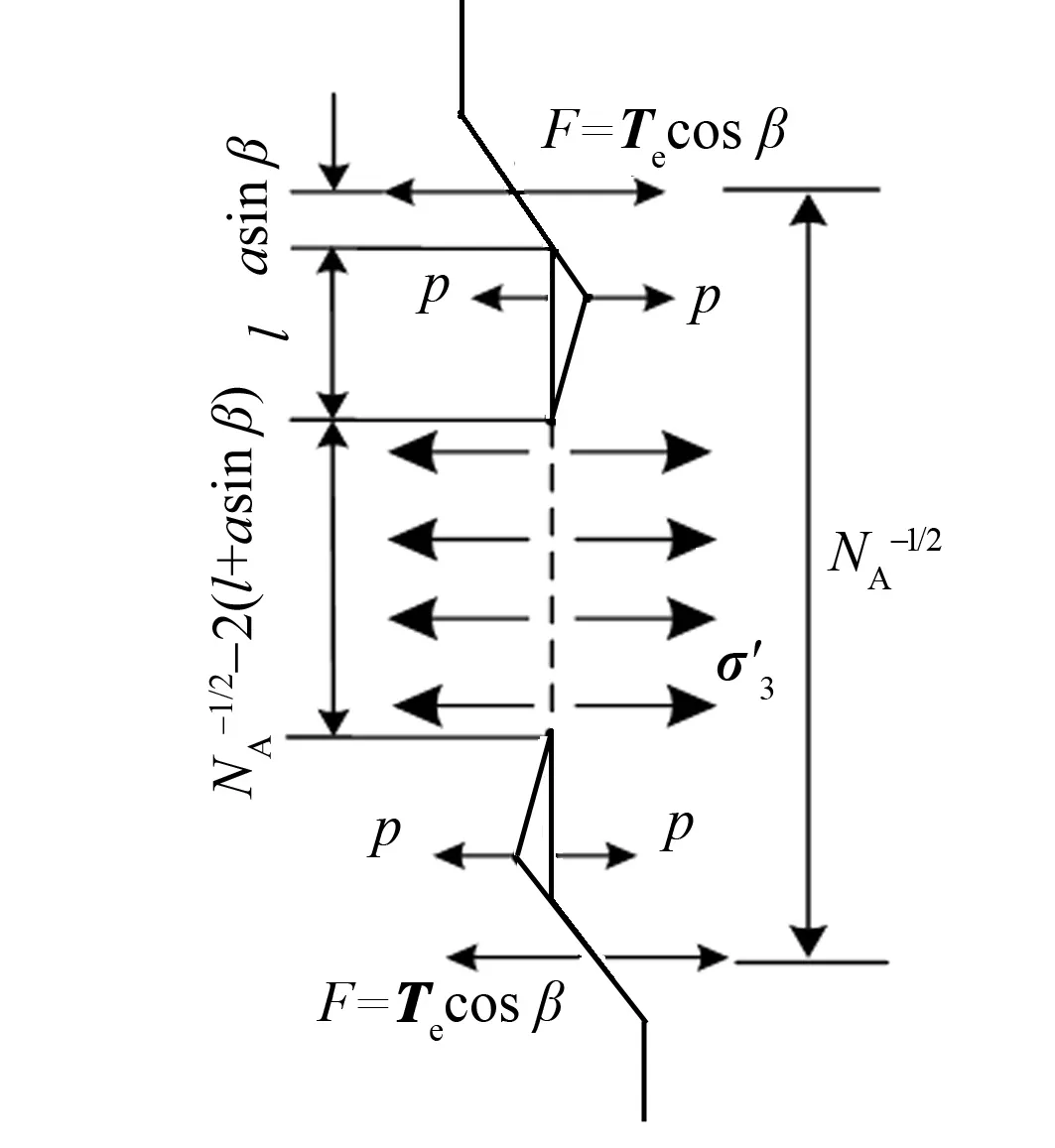
图2 翼形多裂纹相互作用示意图Fig.2 Diagram of interactionof multiple wing cracks
1.2多裂纹间相互作用
前人对裂纹岩石做了不少的研究,但多数都停留在裂纹稀疏分布的基础上,忽略高密度裂纹间的相互作用.以规则排列的双周期雁形裂纹为例,取相邻的两条翼形裂纹,翼裂纹相互作用的力学模型,如图2所示.岩桥间的拉应力[9]为
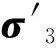
考虑到翼形裂纹的拓展使得岩桥内产生不可忽略的拉应力,进而引起岩桥损伤,翼形裂纹尖端的应力强度因子叠加之后,得
2 渗透压下翼形裂纹的压剪断裂判据
在KⅢ=0的二维模型里,裂纹尖端的应力分量在远场压剪荷载作用下的极坐标[14]为
假设:1) 裂纹在裂纹面出现最不利抗剪组合时,进行延伸扩展;2) 裂纹在剪应力达到起裂的临界值时,开始起裂扩展.为确定开裂角θ0,对式(16)第2个表达式θ进行微分,并令其等于0,可得
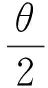
设θ=θ0满足式(17)的要求,由文献[15]得
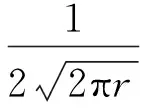
由上述假设可知,裂纹沿裂纹面最不利抗剪组合进行扩展,简化后利用摩尔-库仑强度理论,可得

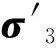
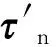
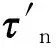
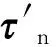
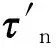
再将式(16),(17)带入式(21),得
1) 当KⅡ=0,θ0=0时,裂纹断裂形式为纯I型断裂,由式(22)计算的断裂韧度KⅠ,C为
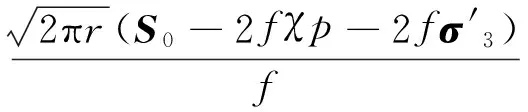
2) 当KⅠ=0时,裂纹断裂形式为纯Ⅱ型断裂,同样由式(22)计算的断裂韧度KⅡ,C为
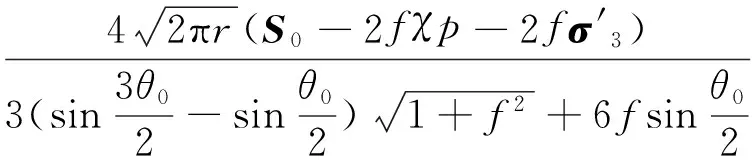
利用式(23)求解出S0的表达式,再代入式(22),可求解出岩石在压剪应力作用下Ⅰ,Ⅱ型裂纹的复合断裂判据,即
3 渗透压下岩石翼形裂纹应力强度因子
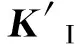
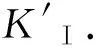
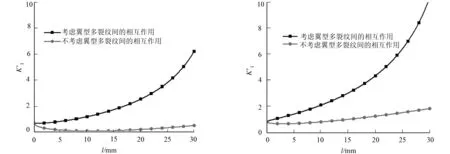
(a) p=0 MPa (b) p=5 MPa图3 考虑与不考虑裂纹间相互作用的值对比Fig.3 values with and without considering cracks interaction

3.2叠加后的应力强度因子KⅠ
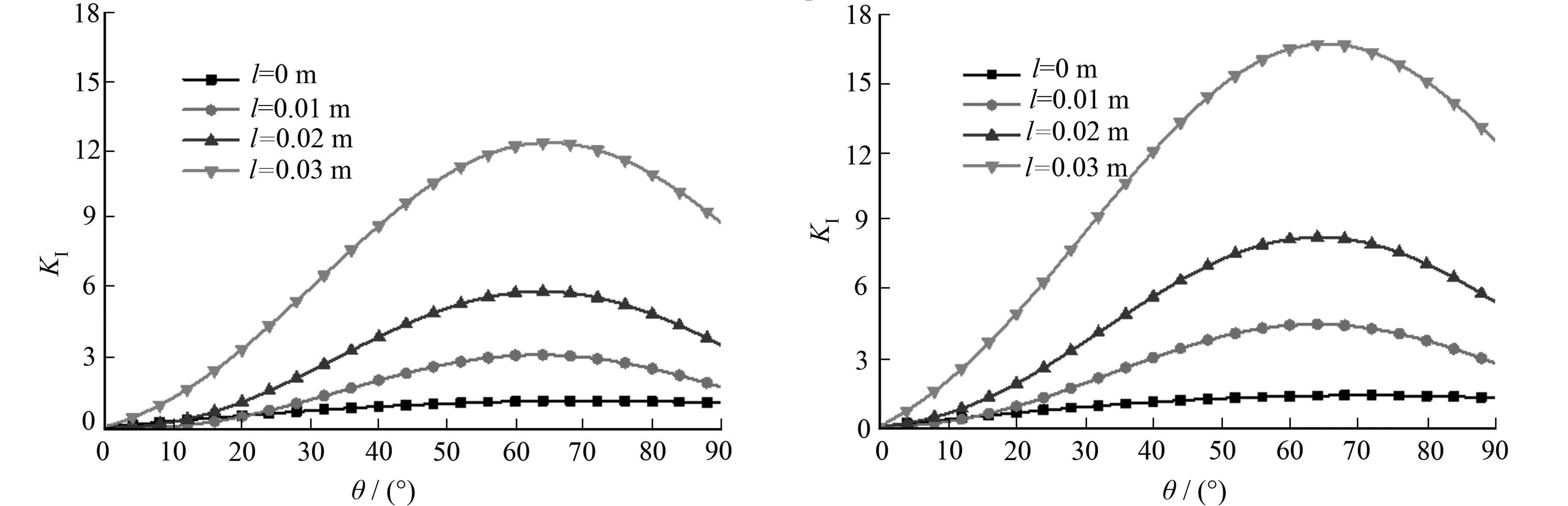
(a) p=0 MPa (b) p=5 MPa 图4 Ⅰ型裂纹应力强度因子随起裂角的变化曲线Fig.4 Curves of type Ⅰ crack stress intensity factor for different crack angles
由图4可知:1) 在相同条件下,应力强度因子随着渗透水压力的增加而增加;2) 当渗透水压力一定时,在不同翼形裂纹长度下,应力强度因子随起裂角的变化规律相同;3) 当起裂角为65°时,应力强度因子达到最大,与按照最大周向应力理论或能量释放率理论计算得到的应力强度因子取极大值(70.5°)时的起裂角不太相符,对比文献[12]的模型可知,由于考虑了裂纹间的相互作用,导致应力强度因子提前到65°,达到最大.
3.3参数敏感性
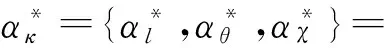
将翼形裂纹长度、裂纹起裂角和裂纹闭合度分别加减10%和20%,其他参数不变,计算应力强度因子结果,如图5所示.图5中:p为渗透水压力.
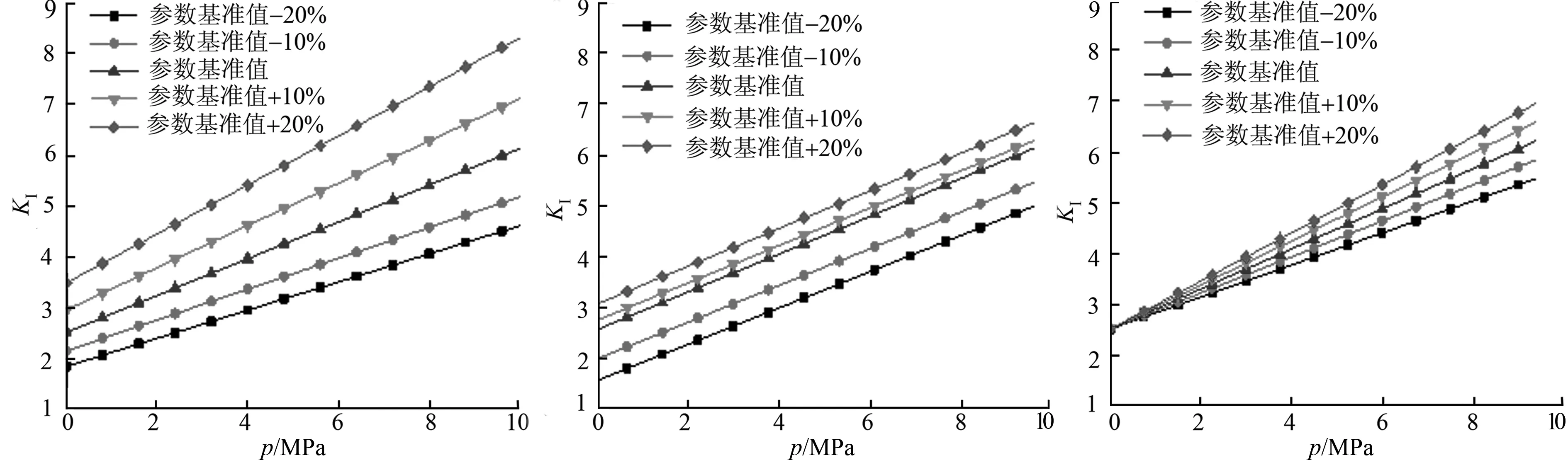
(a) 不同裂纹长度 (b) 不同裂纹起裂角 (c) 不同裂纹闭合度图5 不同参数下裂纹尖端的应力强度因子Fig.5 Stress intensity factor at tip under different parameters
由图5可知:在标准值上下波动的过程中,随着渗透水压力的增加,由翼形裂纹长度引起的裂纹尖端应力强度因子的变化幅度明显大于起裂角和裂纹闭合度引起的,且裂纹闭合度引起的最小.
在渗透水压力p=5 MPa的情况下,对上述其他3个参数进行敏感性分析.同时,为保证各参数之间能进行敏感性的比较,需要对此进行参数无量纲化处理.由文献[18]得敏感性因子计算公式为
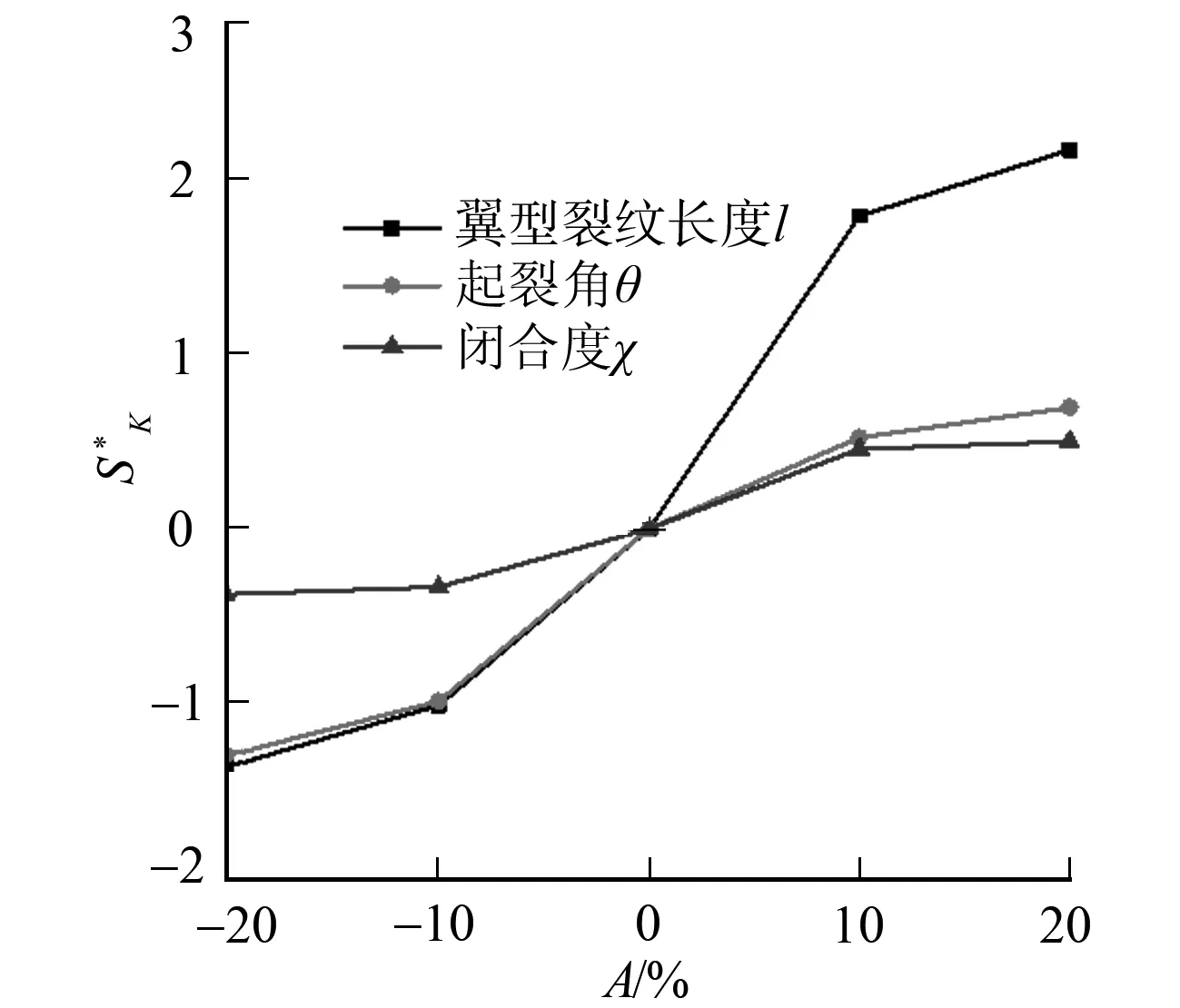
图6 敏感性因子曲线Fig.6 Sensitivity factor curve
敏感性因子曲线,如图6所示.图6中:A为翼型裂纹长度(l)、起裂角(θ)和闭合度(χ)等3个参数的变化幅度.在p=5 MPa的情况下,当参数进行负变化波动时,参数θ和l对应的敏感性因子相差不大,即SK(αl)≈SK(αθ)gt;SK(αχ);当参数进行正变化波动时,参数θ和χ对应的敏感性因子相差不大,SK(αl)gt;SK(αχ)≈SK(αθ).当渗透水达到相当大时,裂隙的闭合程度小范围变化并不会引起χp太大浮动.因此,裂纹尖端应力强度因子对裂纹间闭合程度敏感度小,而裂纹起裂角θ和翼形裂纹长度l直接控制着裂隙的拓展延伸方向,参数敏感性因子相对较大.
4 结论
1) 形裂纹尖端应力强度因子与渗透压、起裂角、翼裂纹长度等有关.渗透压一定时,应力强度因子随起裂角的变化呈近似抛物线关系,岩石翼形裂纹长度越长,应力强度因子越大,越容易达到断裂韧度.
2) 纹间相互作用对裂尖应力强度因子的影响显著,考虑裂纹间相互作用的计算结果显示,应力强度因子提前到65°时达到最大.在岩石含高密度裂纹情况下,考虑裂纹间相互作用很有必要.
3) 基于摩尔-库仑准则,推导考虑裂纹间相互作用的闭合型裂纹的断裂韧度,以及岩石在压剪条件下,Ⅰ,Ⅱ型复合断裂判据.裂纹的断裂韧度与渗透压和裂纹间的相互作用力成反比,两种力的增加都会加速裂纹的拓展.
4) 裂纹尖端应力强度因子对裂纹间闭合程度的敏感性很小,而对裂纹起裂角和岩石翼形裂纹长度的敏感性较大.
[1] 郭少华,孙宗颀,谢晓晴.压缩条件下岩石断裂模式与断裂判据的研究[J].岩土工程学报,2002,24(3):304-308.DOI:10.3321/j.issn:1000-4548.2002.03.008.
[2] LI Yingping,THAM L G,WANG Yuanhan,etal.A modified Kachanov method for analysis of solids with multiple cracks[J].Engineering Fracture Mechanics,2003,70(9):1115-1129.DOI:10.1016/S0013-7944(02)00096-6.
[3] 张卫东,陈士海.考虑初始渗透压力的裂隙岩体本构模型二次开发及其验证[J].华侨大学学报(自然科学版),2017,38(3):319-324.DOI:10.11830/ISSN.1000-5013.201703007.
[4] 席婧仪,陈忠辉,朱帝杰,等.岩石不等长裂纹应力强度因子及起裂规律研究[J].岩土工程学报,2015,37(4):727-733.DOI:10.11779/CJGE201504019.
[5] 席婧仪,陈忠辉,张伟.单轴拉伸作用下不等长裂纹相互影响的断裂力学分析[J].岩石力学与工程学报,2014,33(增刊2):3625-3630.DOI:10.13722/j.cnki.jrme.2014.s2.029.
[6] 王元汉,徐钺,谭国焕,等.改进的翼形裂纹分析计算模型[J].岩土工程学报,2000,22(5):612-615.DOI:10.3321/j.issn:1000-4548.2000.05.023.
[7] HORII H,NEMATNASSER S.Brittle failure in compression: Splitting, faulting and brittle-ductile transition[J].Philosophical Transactions of the Royal Society a Mathematical Physical and Engineering Sciences,1986,319(1549):337-374.DOI:10.1016/0148-9062(88)92337-6.
[8] 李夕兵,贺显群,陈红江.渗透水压作用下类岩石材料张开型裂纹启裂特性研究[J].岩石力学与工程学报,2012,31(7):1317-1324.DOI:10.3969/j.issn.1000-6915.2012.07.002.
[9] 赵延林.裂隙岩石渗流-损伤-断裂耦合理论及应用研究[D].长沙:中南大学,2009.
[10] 中国航空研究院.应力强度因子手册[M].北京:科学出版社,1993.
[11] LI Song,LAJTAI E Z.Modeling the stress-strain diagram for brittle rock loaded in compression[J].Mechanics of Materials,1998,30(3):243-251.DOI:10.1016/s0167-6636(98)00052-0.
[12] 赵延林,王卫军,赵伏军,等.渗透压-应力作用下岩体翼形裂纹模型与数值验证[J].采矿与安全工程学报,2010,27(3):370-376.DOI:10.3969/j.issn.1673-3363.2010.03.015.
[13] 刘涛影,曹平,章立峰,等.高渗压条件下压剪岩石裂纹断裂损伤演化机制研究[J].岩土力学,2012,33(6):1801-1808.DOI:10.3969/j.issn.1000-7598.2012.06.031.
[14] 李世愚.岩石断裂力学导论[M].北京:中国科学技术大学出版社,2010.
[15] 潘别桐,唐辉明.岩石压剪性断裂特性及Ⅰ-Ⅱ型复合断裂判据[J].地球科学,1988(4):59-67.
[16] 俞缙,赵晓豹,赵维炳,等.改进的岩石节理弹性非线性法向变形本构模型研究[J].岩土工程学报,2008,30(9):1316-1321.DOI:10.3321/j.issn:1000-4548.2008.09.009.
[17] 唐胜兰,俞缙,张建智,等.顾及沉积岩应变强化与扩容效应的围岩弹塑性力学状态理论分析[J].华侨大学学报(自然科学版),2016,37(6):691-697.DOI:10.11830/ISSN.1000-5013.201606007.
[18] 朱维申,何满潮.复杂条件下围岩稳定性与岩石动态施工力学[M].北京:科学出版社,1995.
(责任编辑: 黄晓楠英文审校: 方德平)
StressIntensityFactorsandFractureCriterionofRockWingCracksUnderPorePressure
HE Ze1, YU Jin1, ZHANG Jianzhi2, CAI Yanyan1, TU Bingxiong1, LI Shengcai1
(1. Fujian Research Center for Tunneling and Urban Underground Space Engineering, Huaqiao University, Xiamen 361021, China;2. School of Civil Engineering, Chongqing University, Chongqing 400044, China)
In order to discuss the damage of rock wing cracks under seepage pressure in partial closure conditions, a mechanical compression-shear wing cracks model is established with the mutual interaction of multiple cracks and the equation of stress intensity factor at the tip of the wing cracks is deduced. The variation of stress intensity factor with wing cracks length under different initial cracks angles is analyzed by comparing the sensitivity of parameters. Based on Mohr-Coulomb strength condition, the criterion of type Ⅰ and Ⅱ comprehensive cracks under compression and shear stress is obtained by the equation of closure cracks considering the interaction of different cracks. The results indicate that the influence of the cracks interaction and the stress intensity factor is significant and the stress intensity factor is maximum for 65° the initial cracks angle. The stress intensity factor is sensitive to the initial cracks angles and the cracks length, is not sensitive to the closure level of cracks.
pore pressure; rock; wing crack; stress intensity factor; fracture criterion
10.11830/ISSN.1000-5013.201704061
TU 456
A
1000-5013(2017)06-0799-07
2017-04-20
俞缙(1978-),男,教授,博士,主要从事岩土力学与地下工程方面的研究.E-mail:bugyu0717@163.com.
国家自然科学基金资助项目(51374112, 51679093, 51774147); 福建省高校新世纪优秀人才支持计划项目(2015年度); 福建省自然科学基金资助项目(2017J01094); 福建省高校杰出青年科研人才培育计划(2016年度); 福建省厦门市科技计划项目(3502Z20161082); 华侨大学研究生科研创新能力培育计划资助项目(1611404003)
节3.1中的数据,在给定渗透水压力条件下,翼形裂纹尖端应力强度因子随裂纹长度(l)及起裂角(θ)的变化规律,如图4所示.
