设置耗能壁板的新型箱形钢墩柱轴压性能数值分析
2017-11-28罗俊李海锋韩枫李升才
罗俊, 李海锋,2, 韩枫, 李升才
(1. 华侨大学 土木工程学院, 福建 厦门 361021;2. 华侨大学 福建省结构工程与防灾重点实验室, 福建 厦门 361021)

设置耗能壁板的新型箱形钢墩柱轴压性能数值分析
罗俊1, 李海锋1,2, 韩枫1, 李升才1
(1. 华侨大学 土木工程学院, 福建 厦门 361021;2. 华侨大学 福建省结构工程与防灾重点实验室, 福建 厦门 361021)
为探讨设置低屈服点加劲耗能壁板对箱形钢墩柱受力性能的影响机理,采用有限元法对3类设置加劲耗能壁板的新型箱形钢墩柱轴压性能进行数值分析,并探讨设置加劲耗能壁板对箱形钢墩柱的荷载-位移曲线、位移延性系数及承载能力的影响规律.结果表明:耗能壁板高度及宽度对箱形钢墩柱的承载能力和延性影响较大;构件承载能力随耗能壁板高度增大而增大,但随耗能壁板宽度增大而减小;构件延性随耗能壁板高度及宽度增大而增大;加劲肋的厚度、宽度及设置数量均对箱形钢墩柱的承载能力和延性有一定影响.
加劲耗能壁板; 新型箱形钢墩柱; 延性; 承载能力
钢结构中的箱形钢墩柱不仅具有较好的抗弯刚度和抗扭刚度,而且重量轻、刚度大、造价低,具有明显的经济效益.但箱形钢墩柱的壁板较薄,在地震中箱形钢墩柱根部壁板易发生局部屈曲变形,致使箱形钢墩柱的抗震性能急剧恶化.因此,国内外学者对钢墩柱的结构和材料进行了新的开发[1-6].目前,研究较多的是采用加劲肋加固箱形截面钢墩柱,使钢墩柱的延性大为改善[7-10].基于此,本文提出一种震后功能可恢复的新型箱形钢墩柱,并对其受力性能进行数值分析.
1 对比试验概况
采用华侨大学10 MN微机控制电液伺服压剪试验机,在弹性阶段用力加载进行控制,最后用位移加载控制进行轴压试验.轴压试件在四面壁板上开洞,将低屈服点钢板与壁板焊接,并在低屈服点钢板上设置不同形式的加劲肋,如图1所示.试件破坏形态,如图2所示.
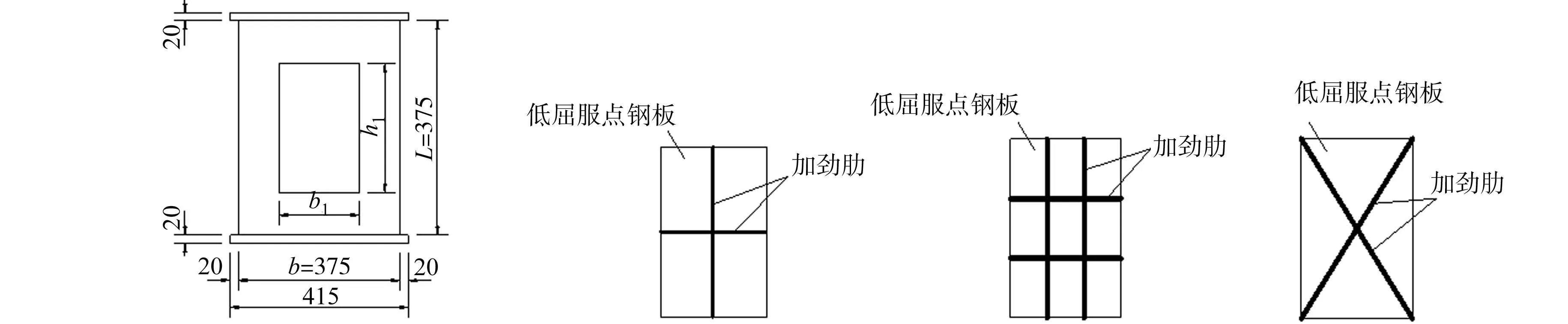
(a) 试件正立面图 (b) 十字形加劲肋 (c) 井字形加劲肋 (d) X形加劲肋图1 试件示意图 (单位:mm)Fig.1 Schematic diagram of specimen (unit: mm)

(a) 试件T-0 (b) 试件T-1 (c) 试件T-2 (d) 试件T-3图2 试件破坏形态Fig.2 Failure mode of specimens
柱的高度L为500 mm;柱截面的高度h和宽度b都为375 mm,不同加劲肋类型的组样T-0~T-3的箱形钢墩柱试件参数,如表1所示.表1中:b1为耗能壁板宽度;h1为耗能壁板高度;十字形及井字形
表1 试验试件设计参数
Tab.1 Parameters of test specimens mm
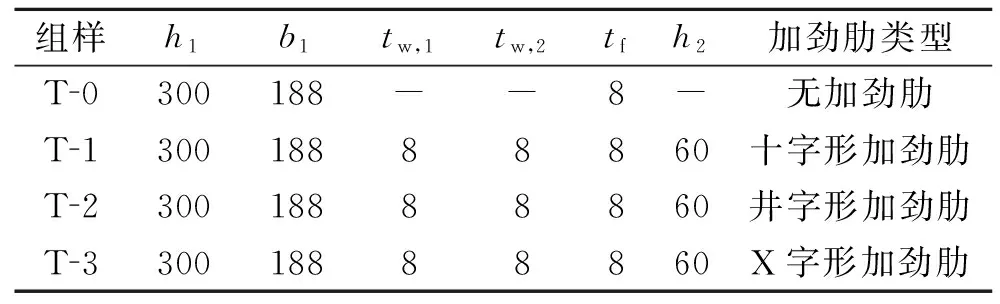
组样h1b1tw,1tw,2tfh2加劲肋类型T 0300188--8-无加劲肋T 130018888860十字形加劲肋T 230018888860井字形加劲肋T 330018888860X字形加劲肋
加劲肋中,tw,1为横向加劲肋厚度,tw,2为竖向加劲肋厚度;X形加劲肋中,tw,1,tw,2分别表示一块加劲肋厚度;tf为箱形钢墩柱四面薄壁及低屈服板的厚度;h2为加劲肋宽度.
2 有限元模型
2.1有限元模型

图3 有限元模型Fig.3 Model of finite element
根据对比试验试件几何尺寸,采用ANSYS有限元软件建立相应的计算模型.有限元模型采用四节点六自由度板壳单元Shell 181,约束四壁板底部的3个方向形成柱底刚性连接,约束柱顶端板X,Y两个方向,对Z方向进行位移控制,从而均匀施加等效面荷载.以单元大小15 mm为控制参数,划分箱形钢墩柱,有限元网格接近正方形,如图3所示.
有限元模型的基本钢材为Q345,低屈服点钢材为Q160,弹性模量E均为206 GPa,泊松比均为0.3,应力-应变关系均采用理想两折线模型.有限元模型中的加劲肋的建模同壁板,加劲肋与低屈服板满焊连接,可以通过重合相应的连接节点实现.
2.2有限元模型与试验结果比较
在柱顶竖向位移加载作用下,部分试件的试验和有限元分析荷载-位移曲线图,如图4所示.图4中:P为作用于试件柱顶的竖向荷载;Δ为对应的柱顶竖向位移.
由图4可知:有限元分析结果与试验结果吻合较好,能反映出竖向荷载作用下箱形钢墩柱的受力特征.为此,采用有限元分析方法进一步研究耗能壁板高度和宽度、加劲肋的厚度和宽度及设置数量等因素对箱形钢墩柱的受力性能的影响规律.
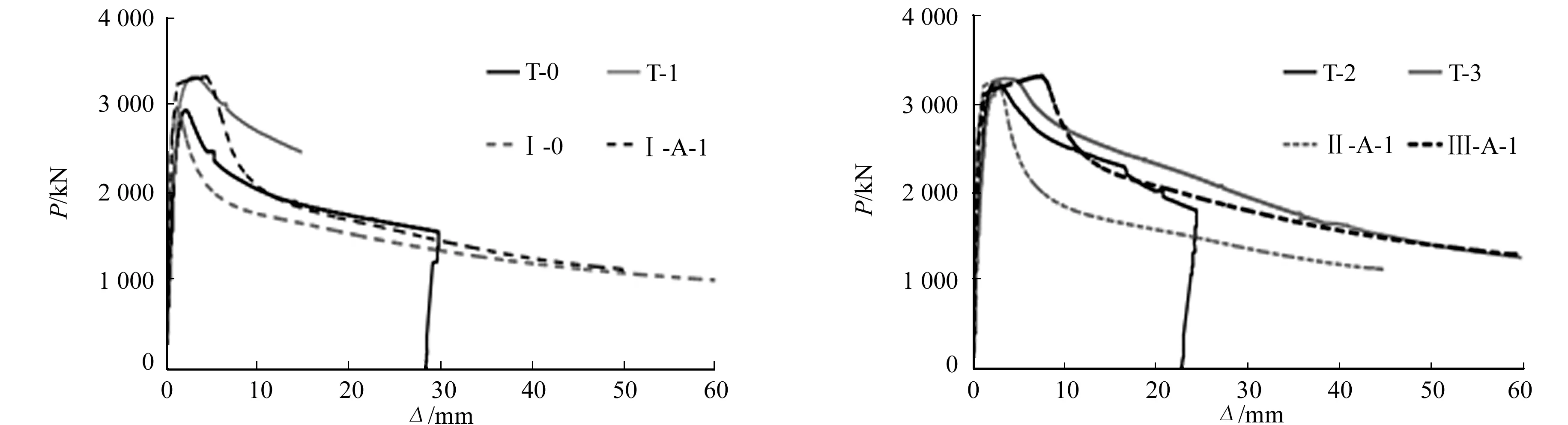
(a) 无加劲肋、十字形加劲肋试件 (b) 井字形加劲肋、X字形加劲肋试件图4 试验和有限元分析荷载-位移曲线Fig.4 Load-displacement curves of experiments and finite element analysis
3 不同类型的加劲肋对比分析
3.1数值分析试件设计
柱的高度L为500 mm;柱截面的高度h和宽度b都为375 mm.数值分析下设置加劲耗能壁板的箱形钢墩柱试件的参数,如表2所示.表2中:Ⅰ-0为无加劲肋;Ⅰ组其他试件为十字形加劲肋,Ⅰ-F组试件设置不同数量加劲肋;Ⅱ组试件为井字形加劲肋;Ⅲ组试件为X字形加劲肋.
表2 数值分析试件设计参数
Tab.2 Parameters of analysis specimens mm
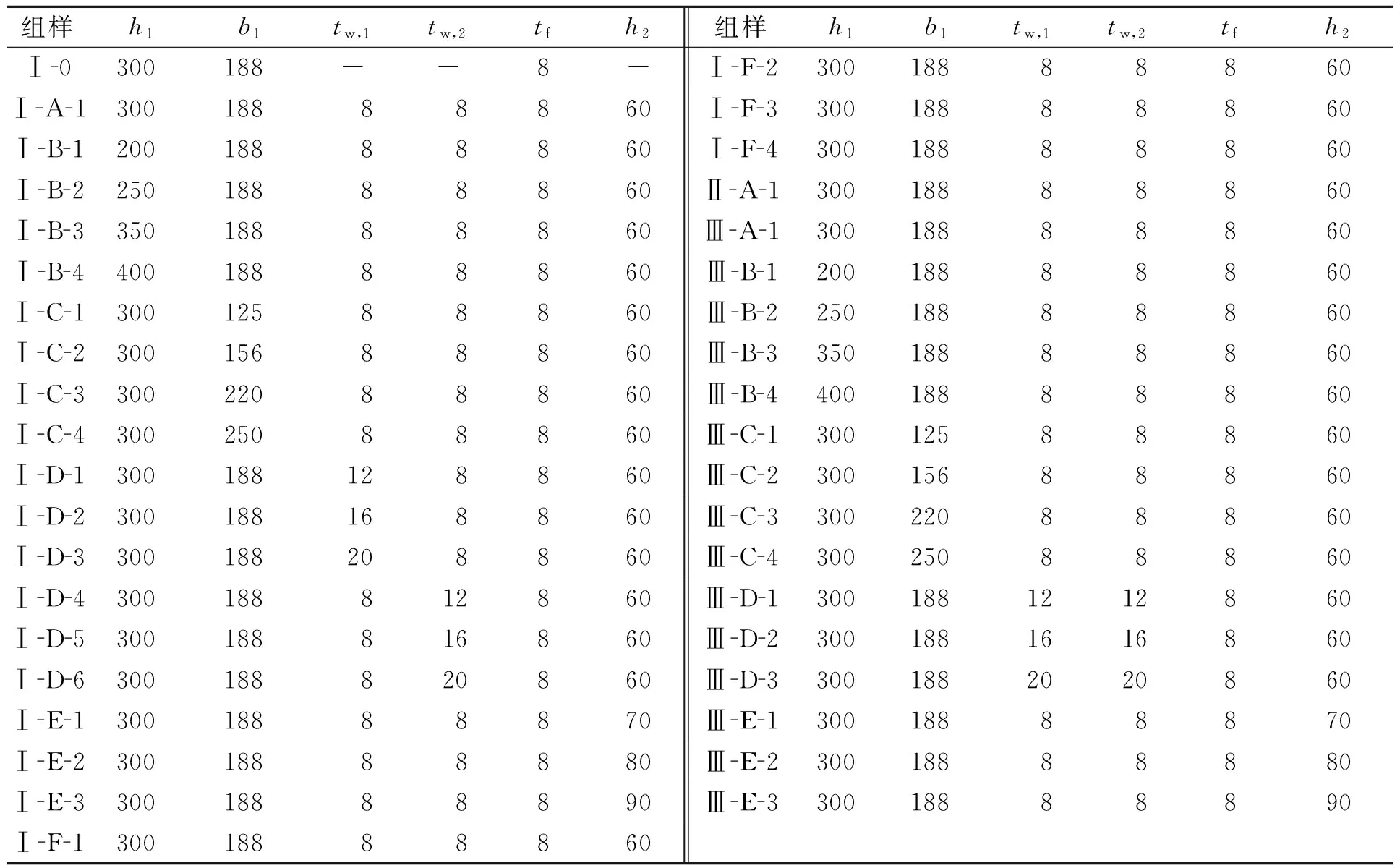
组样h1b1tw,1tw,2tfh2组样h1b1tw,1tw,2tfh2Ⅰ 0300188--8-Ⅰ F 230018888860Ⅰ A 130018888860Ⅰ F 330018888860Ⅰ B 120018888860Ⅰ F 430018888860Ⅰ B 225018888860Ⅱ A 130018888860Ⅰ B 335018888860Ⅲ A 130018888860Ⅰ B 440018888860Ⅲ B 120018888860Ⅰ C 130012588860Ⅲ B 225018888860Ⅰ C 230015688860Ⅲ B 335018888860Ⅰ C 330022088860Ⅲ B 440018888860Ⅰ C 430025088860Ⅲ C 130012588860Ⅰ D 1300188128860Ⅲ C 230015688860Ⅰ D 2300188168860Ⅲ C 330022088860Ⅰ D 3300188208860Ⅲ C 430025088860Ⅰ D 4300188812860Ⅲ D 13001881212860Ⅰ D 5300188816860Ⅲ D 23001881616860Ⅰ D 6300188820860Ⅲ D 33001882020860Ⅰ E 130018888870Ⅲ E 130018888870Ⅰ E 230018888880Ⅲ E 230018888880Ⅰ E 330018888890Ⅲ E 330018888890Ⅰ F 130018888860
为定量分析试件延性大小,引入延性系数[11],其计算公式为μ=Δ85%/Δ75%.式中:Δ85%为承载力下降到极限承载力的85%时,对应的位移值;Δ75%为承载力在峰值点前段中达到极限承载力的75%时,对应的位移值.
3.2十字形加劲肋
3.2.1 不同耗能壁板高度 设置十字形加劲肋试件不同耗能壁板高度h1下的荷载-位移曲线、延性系数及最大荷载对比图,如图5所示.由有限元模拟及延性系数计算公式计算结果可知:随着h1的增大,试件承载力逐渐增大,但h1值增大到一定值后,试件承载力增大不明显,试件延性系数也逐渐提高,但h1值增大到一定值后,试件延性系数反而有所减小.

(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图5 耗能壁板高度对试件受力性能的影响Fig.5 Influence of energy dissipation panel height on mechanical properties of specimens
3.2.2 不同耗能壁板宽度 设置十字形加劲肋试件不同耗能壁板宽度b1下的荷载-位移曲线、延性系数及最大荷载对比图,如图6所示.由有限元模拟及延性系数计算公式计算结果可知:随着b1的增大,试件承载力逐渐减小,试件延性系数逐渐提高.
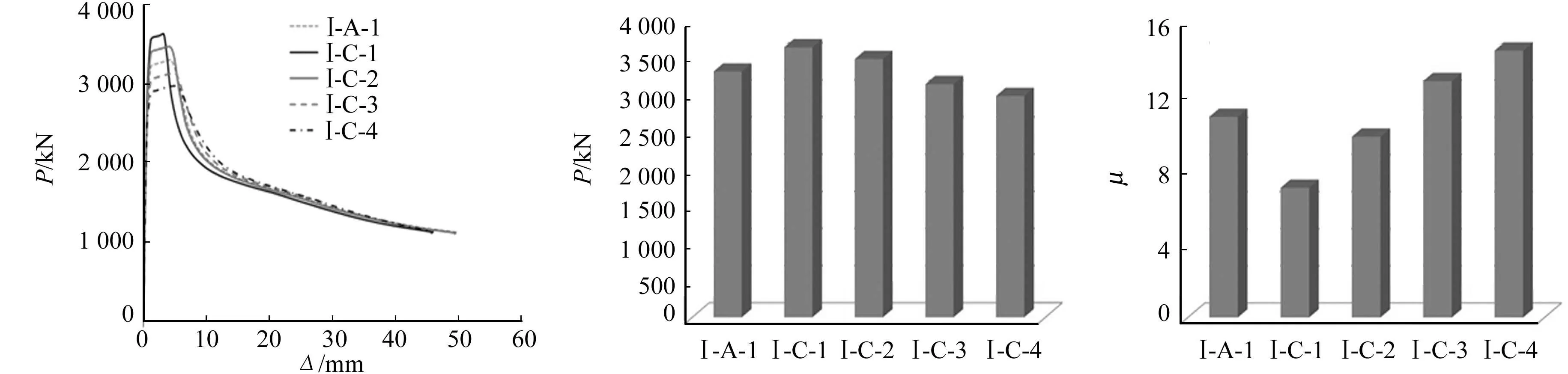
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图6 耗能壁板宽度对试件受力性能的影响Fig.6 Influence of energy dissipation panel width on mechanical properties of specimens
3.2.3 不同加劲肋厚度 设置十字形加劲肋试件不同加劲肋厚度下的荷载-位移曲线、延性系数及最大荷载对比图,如图7所示.由有限元模拟及延性系数计算公式计算结果可知:随着十字形加劲肋中横向加劲肋厚度tw,1的增大,试件承载力变化不大,但试件延性系数有所提高;随着十字形加劲肋中竖向加劲肋厚度tw,2的增大,试件承载力逐渐增大,但试件延性系数有所减小.
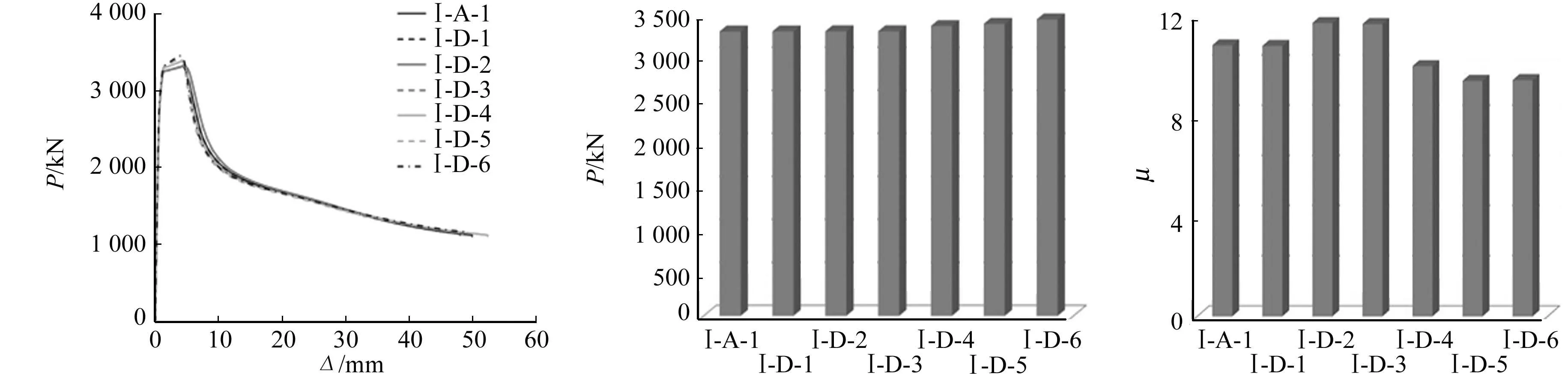
(a) 荷载-位移曲线图 (b) 最大荷载 (c) 延性系数图7 十字形加劲肋厚度对试件受力性能的影响Fig.7 Influence of thickness of cross rib on mechanical properties of specimens
3.2.4 不同加劲肋宽度 设置十字形加劲肋试件不同加劲肋宽度h2下的荷载-位移曲线、延性系数及最大荷载对比图,如图8所示.由有限元模拟及延性系数计算公式计算结果可知:随着h2的增大,试件承载力有所增加,但是增加幅度不大,随着h2的增大,试件延性系数的变化不大.
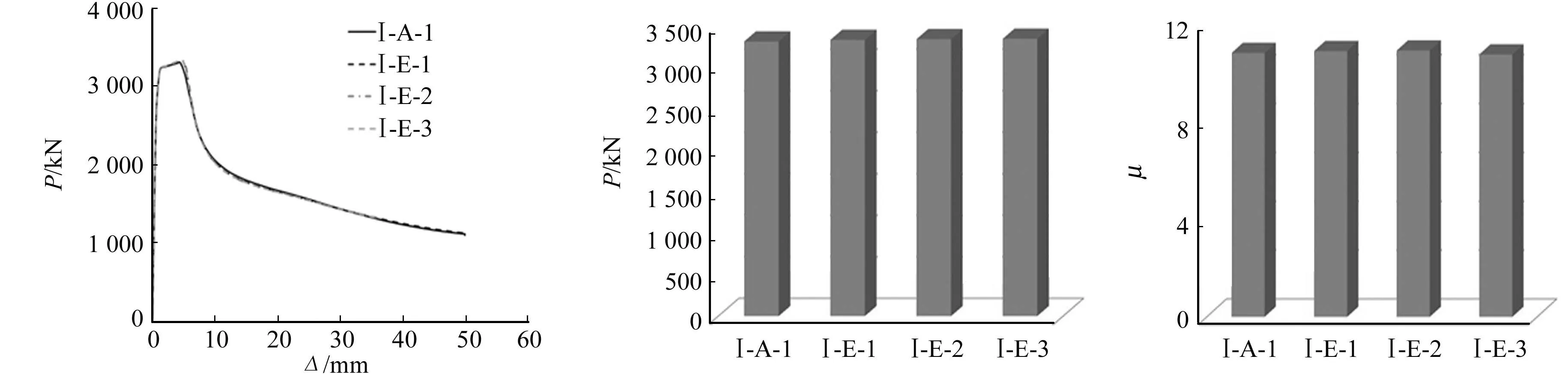
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图8 十字形加劲肋宽度对试件受力性能的影响Fig.8 Influence of width of cross rib on mechanical properties of specimens
3.2.5 不同加劲肋数量 设置十字形加劲肋试件不同加劲肋数量下的荷载-位移曲线、延性系数及最大荷载对比图,如图9所示.图9中:试件Ⅰ-F-1,Ⅰ-F-2分别为设置两、三块竖向加劲肋;试件Ⅰ-F-3,Ⅰ-F-4分别为设置两、三块横向加劲肋.
由有限元模拟及延性系数计算公式计算结果可知:随着设置横向加劲肋数量的增加,试件承载力的变化不大,但试件延性系数反而有所减小;随着设置竖向加劲肋数量的增加,试件承载力有大幅的提高,但试件延性系数有所降低.
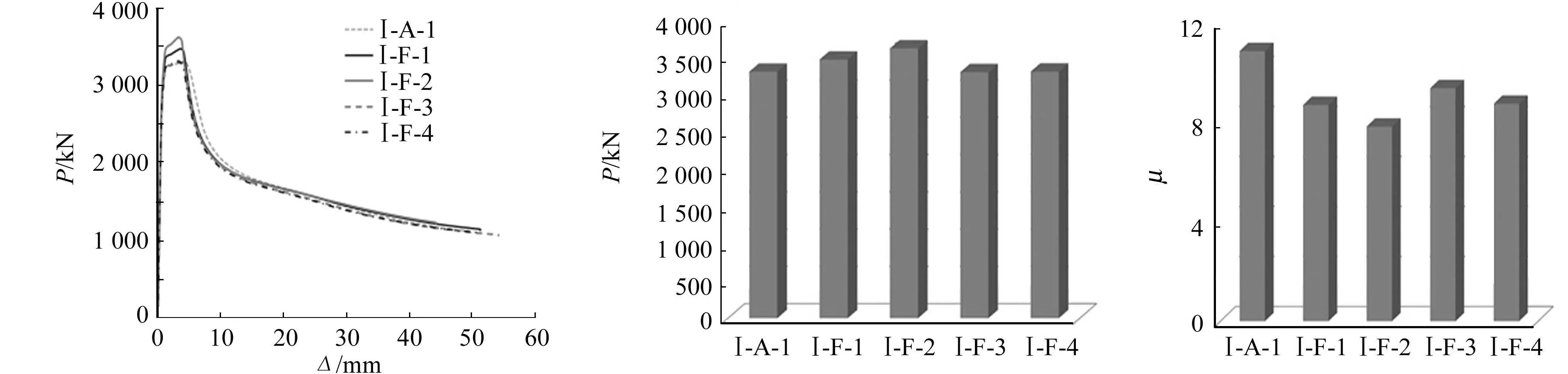
(a) 荷载-位移曲线图 (b) 最大荷载 (c) 延性系数图9 十字形加劲肋设置数量对试件受力性能的影响Fig.9 Influence of number of cross rib on mechanical properties of specimens
3.3X形加劲肋
3.3.1 不同耗能壁板高度 设置X形加劲肋试件不同耗能壁板高度h1下的荷载-位移曲线、延性系数及最大荷载对比图,如图10所示.由有限元模拟及延性系数计算公式计算结果可知:随着h1的增大,试件承载力逐渐增大,但h1值增大到一定值后,试件承载力增大不明显,随着h1的增大,试件延性系数逐渐提高.
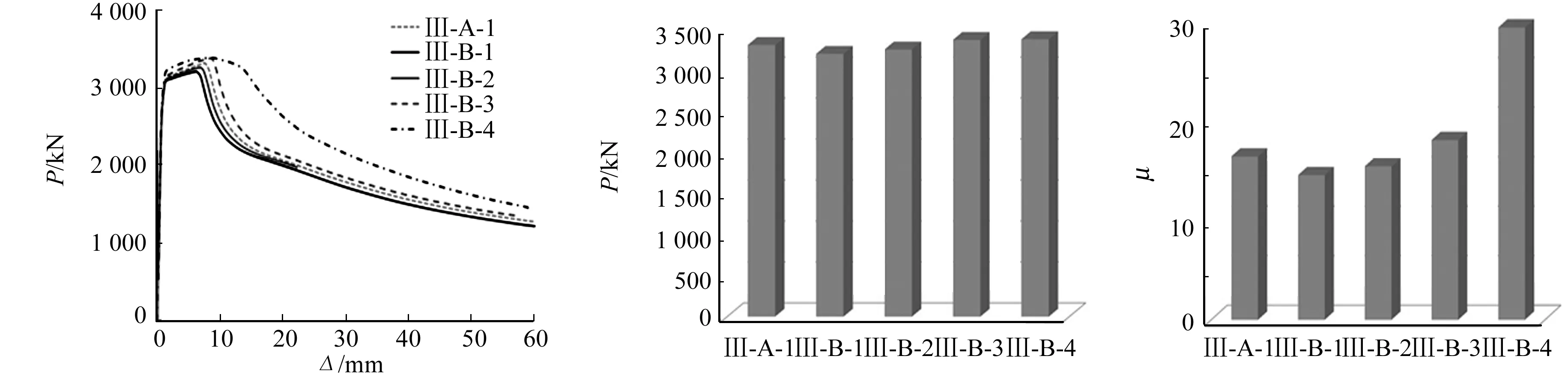
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图10 耗能壁板高度对试件受力性能的影响Fig.10 Influence of energy dissipation panel height on mechanical properties of specimens
3.3.2 不同耗能壁板宽度 设置X形加劲肋试件不同耗能壁板宽度b1下的荷载-位移曲线、延性系数及最大荷载对比图,如图11所示.由有限元模拟及延性系数计算公式计算结果可知:随着b1的增大,试件承载力逐渐减小,试件延性系数逐渐提高.
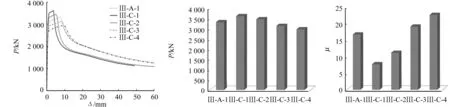
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图11 耗能壁板宽度对试件受力性能的影响Fig.11 Influence of energy dissipation panel width on mechanical properties of specimens
3.3.3 不同加劲肋厚度 设置X形加劲肋试件不同加劲肋厚度tw,1,tw,2下的荷载-位移曲线、延性系数及最大荷载对比图,如图12所示.由有限元模拟及延性系数计算公式计算结果可知:随着tw,1,tw,2的增大,试件承载力逐渐增大,但是增大幅度不明显;随着tw,1,tw,2的增大,试件延性系数有所减小.
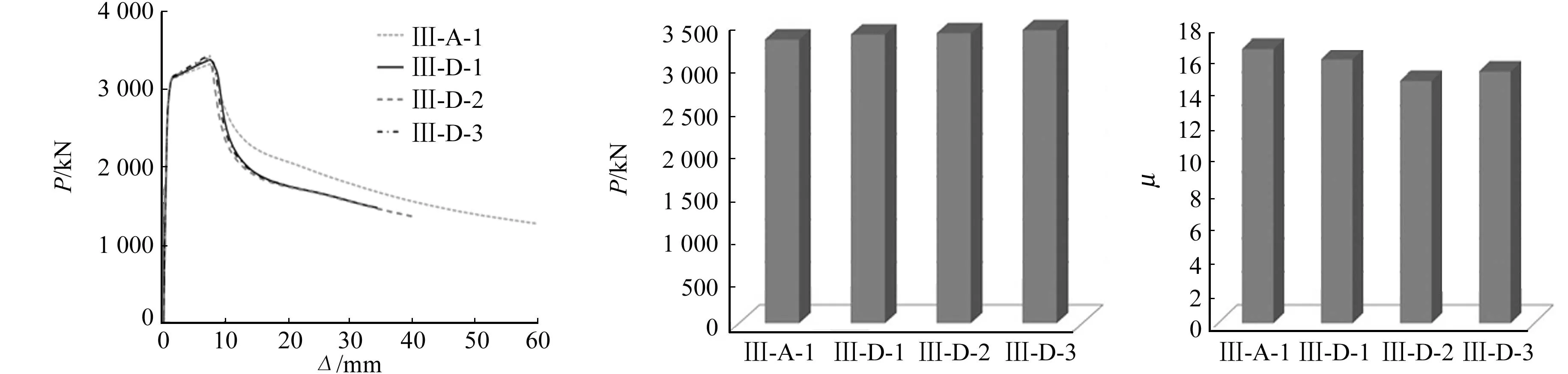
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图12 X形加劲肋厚度对试件受力性能的影响Fig.12 Influence of the thickness of X rib on mechanical properties of specimens
3.3.4 不同加劲肋宽度 设置X形加劲肋试件不同加劲肋宽度h2下的荷载-位移曲线、延性系数及最大荷载对比图,如图13所示.由有限元模拟及延性系数计算公式计算结果可知:随着h2的增大,试件承载力有所增加,但是增加幅度不大;随着h2的增大,试件延性系数变化不大.
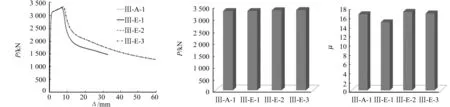
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图13 X形加劲肋宽度对试件受力性能的影响Fig.13 Influence of width of X rib on mechanical properties of specimens
3.4不同类型加劲肋
设置不同类型加劲肋试件的荷载-位移曲线图、延性系数及最大荷载对比图,如图14所示.由有限元模拟及延性系数计算公式计算结果可知:试件中设置加劲肋的3个试件承载力较为接近, X形加劲肋试件比十字形和井字形加劲肋试件的延性性能好;与未设置加劲肋试件相比,设置加劲肋后试件的承载能力和延性均有较大提高.
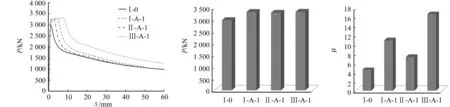
(a) 荷载-位移曲线 (b) 最大荷载 (c) 延性系数图14 不同类型的加劲肋试件对试件受力性能的影响Fig.14 Influence of different types of stiffener specimens on mechanical properties of specimens
4 结论
1) 加劲耗能壁板的设置能提高箱形钢墩柱的承载力和延性;设置3种不同类型加劲肋对构件承载力的影响较小,而对于构件延性性能设置X形加劲肋比设置十字形或井字形加劲肋提高的幅度更大.
2) 对于设置十字加劲肋耗能壁板的箱形钢墩柱,构件承载力随耗能壁板高度h1、竖向加劲肋板厚度tw,2、加劲肋板宽度h2及竖向加劲肋数量的增大而增大;但随耗能壁板宽度b1的增大而减小.构件延性随耗能壁板高度h1、宽度b1、横向加劲肋厚度tw,1的增大而增大;但随竖向加劲肋厚度tw,2及加劲肋数量的增大而减小.
3) 对于设置X形加劲肋耗能壁板的箱形钢墩柱,构件承载力随耗能壁板高度h1、加劲肋厚度tw,1,tw,2及加劲肋宽度h2的增大而增大;但随耗能壁板宽度b1的增大而减小.构件延性随耗能壁板高度h1和宽度b1的增大而增大,但随加劲肋厚度tw,1,tw,2的增大而减小.
[1] USAMI T,GE H B.Ductility of concrete-filled steel box column under cyclic loading[J].Journal of Structural Engineering,1994,120(7):2021-2040.DOI:10.1061/(ASCE)0733-9445(1994)120:7(2021).
[2] GE H B,USAMI T.Cyclic tests of concrete-filled steel box columns[J].Journal of Structural Engineering,1996,122(10):1169-1177.DOI:10.1061/(ASCE)0733-9445(1996)122:10(1169).
[3] USAMI T,GE H B,SAIZUKA K.Behavior of partially concrete-filled steel bridge piers under cyclic and dynamic loading[J].Journal of Constractional Steel Research,1998,41(2):121-136.DOI:10.1016/S0143-974X(97)00007-2.
[4] GE H B,SUSANTHA K A S,SATAKE Y,etal.Seismic demand predictions of concrete-filled steel box columns[J].Engineering Structures,2003,25(3):337-345.DOI:10.1016/S0141-0296(02)00162-1.
[5] 王跃东,高圣彬.内填部分混凝土箱形截面钢桥墩的滞回性能研究[J].四川建筑科学研究,2012,38(1):14-18.DOI:10.3969/j.issn.1008-1933.2012.01.004.
[6] SUSANTHA K A S,AOKI T,KUMANO T,etal.Applicability of low-yield-strength steel for ductility improvement of steel bridge piers[J].Engineering Structures,2005,27(7):1064-1073.
[7] ISMAIL R E S,FATHELBAD F A,ELDIN H,etal.Numerical investigations on dynamic performance of stiffened box steel bridge piers[J].International Journal of Steel Structures,2012,12(2):139-155.
[8] GE H B,USAMI T.Cyclic tests of concrete-filled steel box columns[J].Journal of Structural Engineering,1996,122(10):1169-1177.DOI:10.1061/(ASCE)0733-9445(1996)122:10(1169).
[9] 吉伯海,高圣彬.钢桥抗震与损伤控制设计指南(基础篇)[M].南京:河海大学出版社,2008.
[10] CHEN Shengjin,CHEN Jie.Steel bridge columns with pre-selected plastic zone for seismic resistance[J].Thin-Walled Structures,2009,47(1):31-38.DOI:10.1016/j.tws.2008.04.007.
[11] TAO Zhong,HAN Linhai.Behaviour of fire-exposed concrete-filled steel tubular beam column repaired with CFRP wraps[J].Thin-Walled Structures,2007,45(1):63-76.DOI:10.1016/j.tws.2006.11.004.
(责任编辑: 钱筠英文审校: 方德平)
NumericalAnalysisofNewSteelBoxPierWithEnergyDissipationPlatesUnderAxialCompression
LUO Jun1, LI Haifeng1,2, HAN Feng1, LI Shengcai1
(1. College of Civil Engineering, Huaqiao University, Xiamen 361021, China; 2. Key Laboratory for Structure Engineering and Disaster Prevention of Fujian Province,Huaqiao University, Xiamen 361021, China)
In order to investigate the effect of the low yield point stiffening energy dissipation plates on the mechanical behavior of steel box piers under axial compression, three types of the new steel box piers with different stiffening energy dissipation plates were analyzed using the finite element method. The influences of stiffening energy dissipation plates on load-displacement curves, displacement ductility coefficient and bearing capacity of the steel box piers were discussed. The results show that the height and width of the energy dissipation plates greatly influence the load capacity and the ductility of those steel box piers. The load capacity of the steel box piers is positive correlated to the height of energy dissipation plates, but is negative correlated to the width of the plates. The ductility of the steel box piers is positive correlated to both the height and width of the energy dissipation plates. The effects of the thickness, width and the setting numbers of the energy dissipation plates on the loading capacity and ductility of the steel box piers are obvious.
stiffening energy dissipation plates; new steel box piers; ductility; load capacity
10.11830/ISSN.1000-5013.201701052
TU 391
A
1000-5013(2017)06-0792-07
2017-01-25
李海锋(1983-),男,副教授,博士,主要从事钢结构抗震性能的研究.E-mail:lihaifeng@hqu.edu.cn.
国家自然科学基金资助项目(51408240); 福建省泉州市科技计划项目(2015Z142); 福建省泉州市校地协同创新专项资助项目(2015Z143); 华侨大学中青年教师科研提升资助计划(ZQN-PY312); 华侨大学研究生科研创新能力培育计划资助项目(1611304025)
