居民用户对分时电价的响应潜力评价方法

王媛, 周明

(新能源电力系统国家重点实验室(华北电力大学), 北京市 102206)

居民用户对分时电价的响应潜力评价方法

王媛, 周明

(新能源电力系统国家重点实验室(华北电力大学), 北京市 102206)

为了适应智能电网的发展，促进需求侧资源的合理利用，在分时电价下选取居民小区用户为研究对象，从时间尺度上提出一种刻画其需求响应潜力的指标和综合评价方法。评价指标从需求响应能力和速度2个角度定义了用户每个时段的需求响应潜力，运用经济学中的需求价格弹性矩阵，得到需求响应能力的计算方法。建立分时电价下居民小区综合需求响应潜力的评价模型。该方法实现对居民小区需求响应潜力的量化，为居民需求侧资源的管理提供了依据，从价格的制定与峰时段的划分2个角度指导分时电价的制定。算例分析证明所提指标的合理性、评价方法的普适性与有效性。

需求响应潜力; 分时电价; 电价弹性矩阵; 爬坡率; 评价

0 引 言

智能电网的发展加之智能家居的普及，以及电力市场改革带来的价格激励，使得居民用户在需求响应中发挥出越来越重要的作用。需求响应(demand response, DR)作为一种高效负荷管理工具不仅提高了电力系统在尖峰时刻的运行可靠性，且有助于电网更好地消纳间歇性能源发电。需求响应项目的开展改变了单纯依靠增加装机容量来缓解电网调峰压力的模式，用户可通过需求响应项目主动响应激励机制，调整用电模式参与“削峰填谷”，使负荷特性呈现“柔性特征”[1]。电价作为电力市场最有效的经济调节杠杆，是需求响应的重要激励措施。峰谷分时电价是目前我国广泛采用的激励政策，通过电价信号引导用户采取合理的用电行为，用户在电价激励下的用电行为特征又反过来影响峰谷分时电价的制定。因此，为了制定合理的分时电价以最大程度地激发用户的响应能力，研究用户在不同分时电价下的响应潜力非常必要。

不同类型用户的响应潜力在不同的空间、时间维度上具有显著的差异性。需求响应的空间维度特性是指不同用户在不同空间范围上的响应特性，例如单一用户、区域用户、聚合用户等；而时间维度特性则反映了用户在不同时间尺度上的响应特性，例如，小时、日、月、年等。已有的文献多针对不同用户响应的空间特性开展研究，少有针对需求响应的时间特性进行研究的。文献[2-4]将用户分成工业、商业和居民负荷，得到了每类用户的总体需求响应削减量。文献[5]在确定单个用户需求响应削峰容量的基础上，按照网络拓扑结构将需求侧响应对负荷的影响落实到具体的每个节点。文献[6]建立了传统需求侧管理、智能互动、电动汽车并网及其组合场景下潜力评估的数学模型，并对广东电网的需求响应潜力进行了评估。上述研究分别从不同的空间维度对用户响应潜力进行了评估，未涉及细致刻画用户日内不同用电时段的响应潜力。由于分时电价是针对不同用户不同用电时段采取不同的电价政策，因而仅仅考察用户的整体需求响应能力难以准确揭示用户响应的时段特性，需对不同用户在不同时段的响应潜力进行研究，才能有效指导分时电价的制定。

近年来，需求响应试点工作已在我国工业、商业用户中逐步展开。由于居民电价水平偏低，至今对居民用户响应特性的研究十分缺乏[7]。随着我国电力市场革新的不断推进，交叉补贴逐步取消，居民电价可能上涨。同时，居民生活水准的提高使家庭用电量不断增加，电费支出在家庭消费的占比会明显提高，居民用户参与需求响应的积极性也会得到极大的调动[8-9]。从北美及欧洲智能电网试点工程采集的相关数据分析可知，居民用户参与需求响应的削峰效果远远高于其他类型用户[6,10]。可见，随着我国智能电网与电力市场化改革的不断推进，居民用户的需求响应潜力是值得重视的。然而现在对居民用户需求响应潜力的评价与分析方法仍十分缺乏。文献[11]提出用户最大用电量、调用时间框架、DR项目等因素决定用户负荷削减的潜力；文献[12]通过调查问卷方式分析需求响应的潜力，得出用户可接受程度是影响DR潜力的关键；文献[13]模拟用户对需求响应项目的不同策略，提出需求响应潜力受到季节因素以及调用时间的影响。上述研究仅对影响需求响应潜力的因素进行了分析，却并未给出居民需求响应潜力的具体定义与量化方法。

基于上述分析，本文选取居民小区用户为研究对象，试图从时间尺度上提出刻画居民用户需求响应潜力的指标和评价方法。首先从需求响应能力和需求响应速度两个方面定义了用户每个时段负荷的需求响应潜力，将用户不同时段的需求响应能力定义为其对削峰填谷的贡献量，并用经济学中弹性系数的概念对其进行了量化；将需求响应速度定义为该时段负荷响应电价激励的快慢，并借鉴发电侧资源中爬坡率的概念对其进行了描述。然后给出了居民小区用户需求响应潜力的具体量化评估方法。最后，基于实测数据，从平均需求响应潜力与响应潜力分布的角度比较了不同用户的响应潜力；分析电价拉开比与峰时段划分对居民小区需求响应潜力特性的影响；讨论了该评价方法对电价弹性系数变化的稳健性。

1 分时电价下需求响应潜力定义

本文将分时电价下的需求响应潜力定义为用户根据自己的用电习惯和偏好，响应分时电价，主动改变用电模式，对区域整体负荷实现削峰填谷可能性的大小。因而从需求响应能力和需求响应速度2个角度刻画不同时段用户在分时电价下的响应潜力。

1.1 需求响应能力

本文将t时刻用户的需求响应能力定义为：受分时电价激励机制驱动，实现削峰填谷的过程中，负荷在t时刻的响应量。处于电价峰时段的负荷在削峰填谷过程中的响应量由负荷自身的削减量与转移到谷时段的转移量2部分组成；处于电价平时段的负荷在削峰填谷过程中的响应量为平时段到谷时段的负荷转移量；谷时段的削峰填谷能力体现在谷时段负荷在分时电价前后的增量。根据上述的定义，可将电价峰、平、谷时段的负荷需求响应能力分别表示为

(1)

式中：Ra(t)表示t时刻负荷的需求响应能力,kW·h；ΔLff(t)为分时电价前后电价峰时段负荷自身的削减量，kW·h；ΔLfg(t)为分时电价前后电价峰时段向谷时段的负荷转移量，kW·h； ΔLpg(t)为分时电价前后电价平时段向谷时段的负荷转移量，kW·h；ΔLgg(t)为分时电价前后电价谷时段负荷的增量，kW·h；Tf为电价峰时段；Tp为电价平时段；Tg为电价谷时段。

1.2 需求响应速度

需求响应能力从负荷响应幅值的角度反映了其需求响应潜力，本节从负荷响应速率的角度，定义了需求响应速度来衡量负荷响应电价激励的快慢。负荷对激励的响应速度由其自身的负荷曲线特性决定，若负荷变化的斜率越陡峭，意味着其响应激励的速度越快、需求响应潜力越大，具有较大的可能性参与到快速需求响应项目中。因此，本节将负荷在t时刻的需求响应速度定义为负荷变化的快慢，具体可表示为

(2)

式中：Rs(t)为t时刻负荷的需求响应速度， (kW·h)/h；L(t)为t时刻的负荷值，kW·h。

1.3 需求响应综合潜力

综合上述2个分时电价下t时刻用户的需求响应特性，并对其进行归一化处理后便得到评价用户需求响应潜力的综合指标。则评价t时刻负荷需求响应潜力的综合指标可表示为

Rp(t)=Ra(t)·Rs(t)

(3)

式中Rp(t)表示t时刻负荷的需求响应潜力。

2 分时电价下负荷需求响应潜力的评价模型

在定义了需求响应潜力的情况下，引入经济学中的弹性系数，对分时电价激励下负荷需求响应能力进行计算，并给出基于实测数据的需求响应速度计算方法。

2.1 负荷需求响应能力计算方法

2.1.1用电需求价格弹性系数

电力负荷的弹性系数表示在一定时期内电价变化所引起的用户用电需求量变化的百分比，其通用公式[14-15]可表示为

(4)

式中：E为电能的需求弹性系数；Δρ为电价的变化，元/(kW·h)；Δd表示基于价格所产生的用电需求量的变化，kW·h；ρ0和d0分别为分时电价前的电价和电力需求量。

2.1.2分时电价前后负荷的改变量

分时电价前后负荷的改变量由负荷的自身的削减量与转移量共同决定，其中，负荷自身的削减量与自弹性系数对应，转移量与交叉弹性系数对应。因此，当负荷曲线的数据维数为N时，分时电价前后t1时刻的负荷改变量为

(5)

式中：t2为负荷曲线中的采样时刻，当t2=t1时，EL(t1,t2) ≤0为自弹性系数，当t2≠t1时，EL(t1,t2) ≥0为交叉弹性系数；L0(t1)为t1时刻的负荷量；ρ0(t2)为分时电价前t2时刻的电价；ρ(t2)为分时电价后t2时刻的电价。

令λL(t1)表示实施分时电价后负荷L在t1时刻的用电量变化率，则有

(6)

令k(t2)表示t2时刻分时电价前后的电价浮动比，并将其定义为[16]

(7)

则式(6)可以改写成

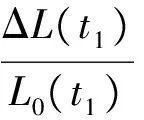
(8)

因此，当t1，t2分别属于电价峰、平、谷时段时，其用电量变化率为

(9)

式中：Tf、Tp、Tg分别表示电价的峰、平、谷时段；t1为其中的任一时段；λfp、λfg和λpg表示负荷转移的效果；λff和λgg描述在峰时段和谷时段削峰填谷效果；由于在电价高峰时，kfgt;0，在平段时，kp=0，在电价谷时，kglt;0，因此λfp、λfg和λpg均为正数，又由于E(t1)lt;0，因此λfflt;0，而λgggt; 0。

2.1.3分时电价前后负荷需求响应量

基于上述分时电价下负荷变化的分析与电价峰、平、谷时段的负荷需求响应能力定义，可知负荷需求响应量具体的计算公式为

(10)

又由式(8)可知，λ(t1)由EL(t1,t2)与k(t2)决定，而在具体的分时电价下k(t2)已知；负荷的弹性系数EL(t1,t2)可基于负荷类型的划分，通过用户的上报或社会调查来获得，具体方法可参考文献[17-18]。

2.2 负荷需求响应速度计算方法

根据第1节的定义可知，居民小区用户在时刻t1的需求响应速度由其负荷曲线在该点的导数决定。而由于实测数据的离散性，负荷曲线呈现出不连续的特点，具有不可导的负荷尖峰时刻，因而不能采用适用于连续函数的求导法对负荷变化的速率进行计算。因此本节根据实测数据的采样间隔Δt，将t时刻负荷的需求响应速度定义为负荷在与t时刻相邻的2个时间间隔间的变化率的平均值，其表达式如(11)所示：

(11)

式中：Rs(t)表示t时刻负荷的需求响应速度；L(t-Δt)为t-Δt时刻的负荷值；L(t+Δt)为t+Δt时刻的负荷值；Δt表示实测数据的采样时间间隔。

2.3 负荷需求响应潜力综合计算方法

将上述需求响应能力与需求响应速度的计算公式代入式(3)，即可得到t时刻负荷需求响应综合潜力指标Rp(t)。则居民用户日平均需求响应潜力可表示为

(12)

式中：Rp表示居民用户日负荷平均需求响应潜力；N是居民日负荷数据的采样点数。

3 仿真算例分析

3.1 数据描述

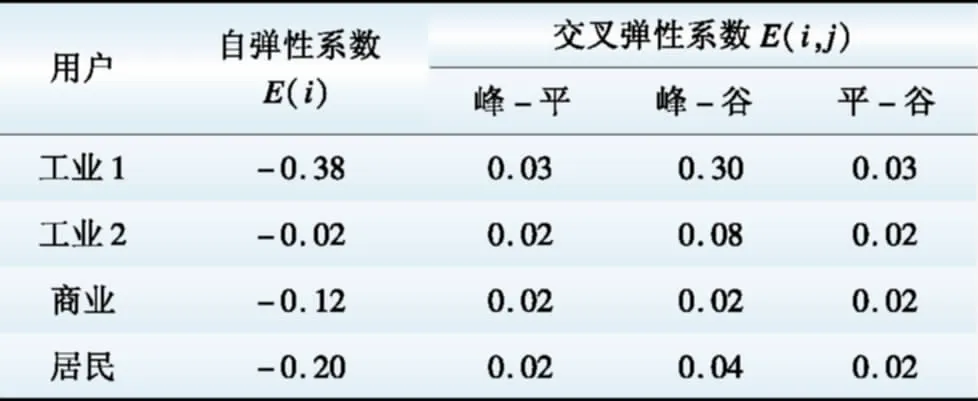
本文选取3个居民小区的整体日负荷曲线(用电量)，用MATLAB工具对不同分时电价政策下其需求响应潜力特性进行分析。每个居民小区由500家居民用户组成，用电量采样的时间间隔为30 min。该地区不同行业的电价弹性系数如表1所示。

表1某地电力负荷分类及用户负荷特性
Table1Loadclassificationandcharacteristicsinaspecificarea

3.2 仿真结果及分析

如图1—3所示为3个不同居民小区在相同的分时电价下日负荷(采样点为48个)的潜力分布情况。居民小区1 的日负荷曲线中，18：00点负荷尖峰时刻的需求响应潜力最大。而居民小区2 的日负荷中的需求响应最大值与最大负荷未能在同一时刻取得，这是因为最大负荷处于电价平时段，分时电价前后向谷时段转移的负荷量少，远远小于电价峰时段负荷的自身削减量与向谷时段转移量之和；同处于电价峰时段的17：30的负荷值虽然大于18：00的负荷值，但是由于18：00负荷的需求响应速率更大，综合考虑两方面的因素，该小区在18：00的负荷具有最大的需求响应潜力。居民小区3的需求响应潜力最大值在处于电价峰时段的17：30取得。

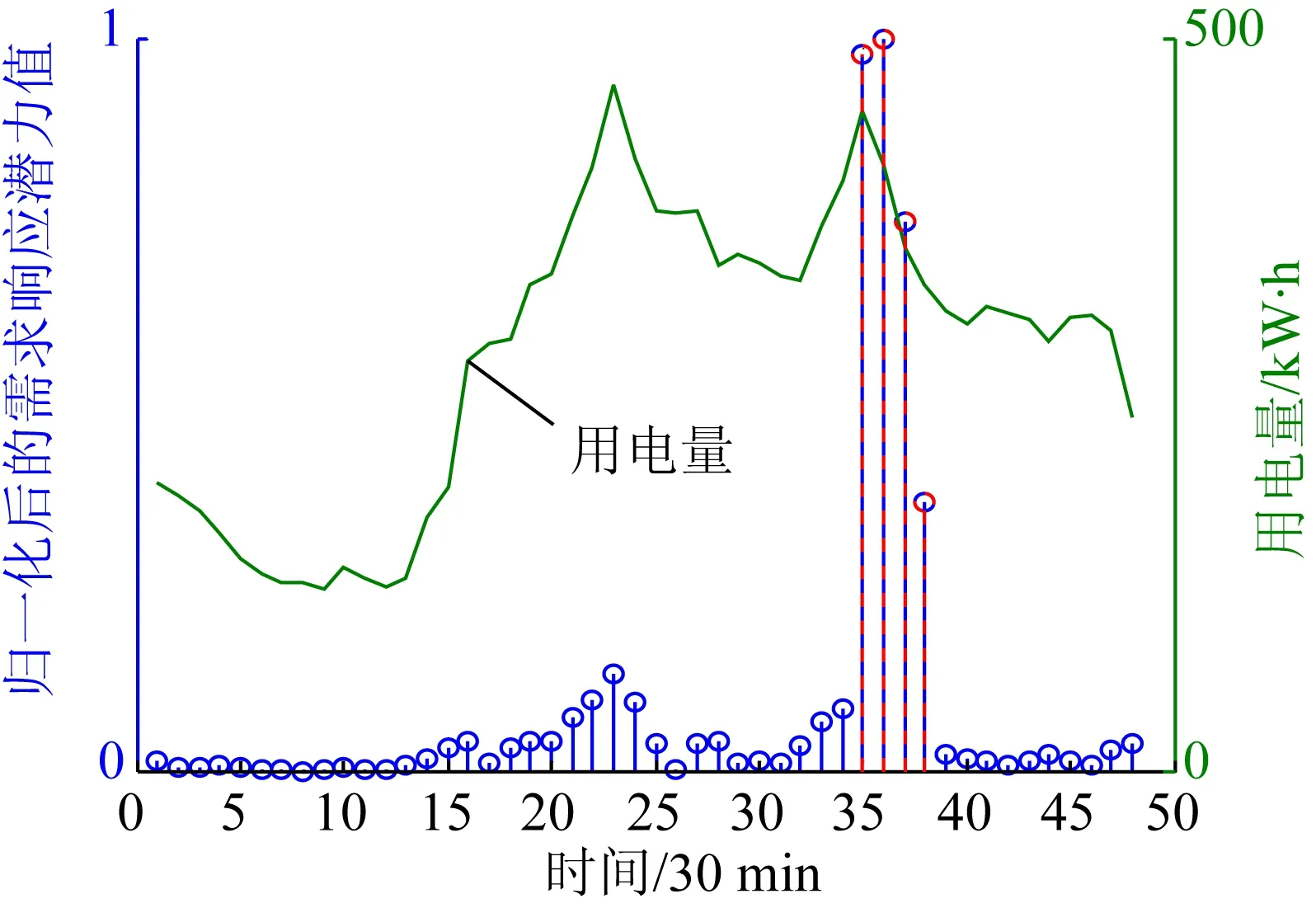
图1 居民小区1日负荷的需求响应潜力分布Fig.1 Demand response potential distribution ofdaily load in residential area 1

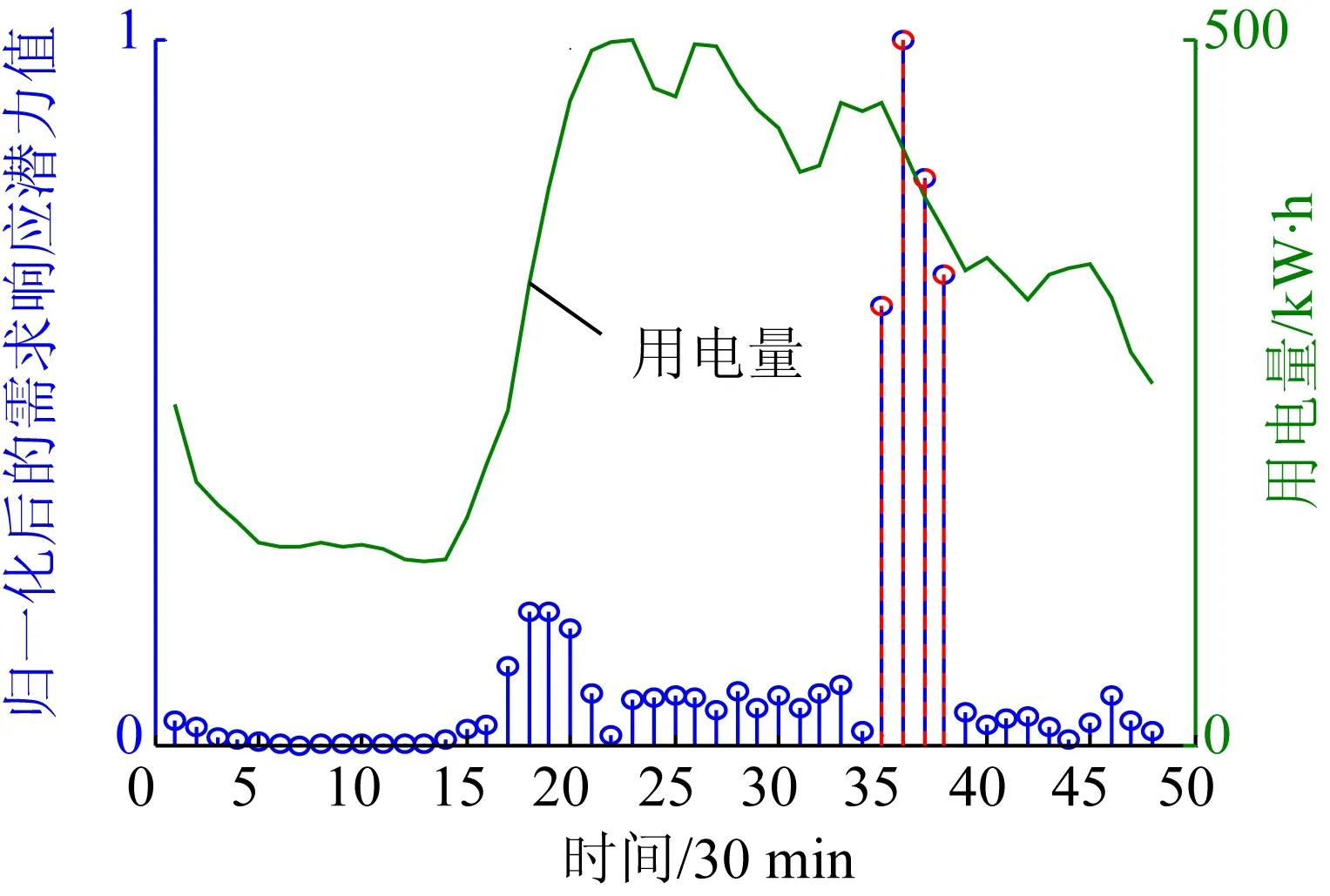
图2 居民小区2日负荷的需求响应潜力分布Fig.2 Demand response potential distribution ofdaily load in residential area 2

图3 居民小区3日负荷的需求响应潜力分布Fig.3 Demand response potential distribution ofdaily load in residential area 3

图4比较了3个不同居民小区的日负荷需求响应潜力分布，表2所示为归一化后不同居民小区同一日峰时段中不同时刻的需求响应潜力与日均需求响应潜力。其中居民小区2的日均需求响应潜力最大为0.065 1，在18:00点达到其需求响应潜力的最大值0.616 0；而居民小区1、3的需求响应潜力分别在18:00与17:30达到其最大值1.000 0和0.313 7。此外，由表中信息计算可得，居民小区1、2、3高峰时段的平均需求响应潜力分别为0.590 4、0.476 2、0.253 8。由此可知，从负荷整体的需求响应潜力来看，居民小区2的用户较其他2个小区的用户在该电价政策下具有更大的需求响应潜力；若需最大程度地调动用户在电价峰时段的需求响应潜力，则对居民小区1的用户实施该电价政策的响应效果最理想。

图4 居民小区1、2、3在同一电价政策下的需求响应潜力Fig.4 Demand response potential of residentialarea 1,2,3 under same tariff

图5所示为居民小区1在表3中所示的不同分时电价政策(不同电价拉开比)下的日负荷需求响应潜力分布。从图5中可以看出，对于该居民小区的用户而言，电价拉开比越大，其需求响应潜力越大，4种电价政策中，分时电价机制D能最大程度激发该小区用户的需求响应潜力。

图5 居民小区1在不同电价拉开比下的需求响应潜力Fig.5 Demand response potential of residentialarea 1 under different price ratios

图6比较了居民小区1的日负荷需求响应潜力在不同峰谷平时段划分下的分布。当峰时段为17：00—19：00时，该小区日负荷的平均需求响应潜力最大为0.060 8，当峰时段前移(16：00—18：00)或者后移(18：00—20：00)1 h，其平均需求响应潜力分别为0.058 8、0.037 1。而负荷高峰时段多分布在17：00至19：00之间，因此，可以得到如下结论：当电价高峰时段与负荷峰时段重合度越高，该电价政策越能激发用户的需求响应潜力。

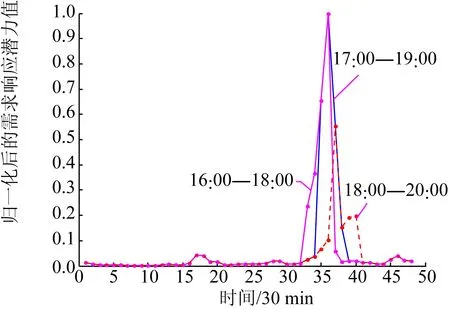
图6 居民小区1在不同峰时段划分下的需求响应潜力Fig.6 Demand response potential of residentialarea 1 under different peak periods

考虑到调研统计过程中存在的偶然因素和误差会影响居民电价弹性系数的精度，因此，图7比较了在不同电价弹性系数下居民用户需求响应潜力的分布。从图7可以看出电价弹性系数的变化未能改变居民用户响应潜力分布的整体趋势，弹性系数的变化仅仅改变了用户不同时段需求响应潜力的绝对大小，相对大小未发生较大变化。在不同电价弹性系数下，居民小区1中用户需求响应潜力的最大值都在19：00取得；且电价峰时段的需求响应潜力远远大于电价谷时与电价平时段。据此可以得出，本文中居民需求响应潜力的定义对于电价弹性系数在时间尺度上具有较好的稳健性，用户不同时段的潜力分布趋势受电价弹性系数影响较小。因此，所提方法可用于指导不同地区用户电价峰、平、谷、时段的划分。

图7 居民小区1在不同弹性系数下的需求响应潜力Fig.7 Demand response potential of residentialarea 1 under different elasticity matrices

4 结 论

本文从响应能力和响应速度2个方面定义了评价用户在分时电价下需求响应潜力的指标，并基于电价弹性矩阵建立了居民小区日负荷响应潜力评价模型。算例比较了不同分时电价激励对居民日响应潜力的影响，给出了分时电价下不同居民小区不同时段的需求响应潜力特性；研究了不同电价拉开比与不同峰时段对居民小区负荷响应潜力分布的影响；讨论了该评价方法对电价弹性系数变化的稳健性。结果表明：电价拉开比在一定范围内与居民用户的响应潜力呈正相关；电价高峰时段与负荷峰时段重合度越高，居民用户在该分时电价政策下的需求响应潜力越大。该评价方法对电价弹性系数具有较好的稳健性，对不同区域居民用户的响应潜力评价具有普适性。

研究工作对用户响应电价潜力进行了合理的量化与评价，能指导分时电价的制定；同时所提供的需求响应潜力评估和预测值可用于用户或其聚合商参与电力市场交易的决策指导。

致谢

本文中实验数据由Electric Ireland and SEAI提供，在此向他们表示衷心的感谢。

[1] 杨旭英, 周明, 李庚银. 智能电网下需求响应机理分析与建模综述[J]. 电网技术, 2016, 40(1): 220-226.

YANG Xuying, ZHOU Ming, LI Gengyin. Survey on demand response mechanism and modeling in smart grid[J]. Power System Technology, 2016, 40(1): 220-226.

[2] 李亚平, 王珂, 郭晓蕊, 等. 基于多场景评估的区域电网需求响应潜力[J]. 电网与清洁能源, 2015, 31(7): 1-7.

LI Yaping, WANG Ke, GUO Xiaorui, et al. Demand response potential based on multi-scenarios assessment in regional power system[J]. Power System and Clean Energy, 2015, 31(7): 1-7.

[3] 苏卫华, 储琳琳, 张亮, 等. 考虑需求侧管理的负荷预测方法研究[J]. 华东电力, 2010, 38(8): 1236-1239.

SU Weihua, Chu Linlin, ZHANG Liang, et al. Study on load forecast method considering demand side management[J]. East China Electric Power, 2010, 38(8): 1236-1239.

[4] 曾鸣, 李娜, 王涛, 等. 兼容需求侧资源的负荷预测新方法[J]. 电力自动化设备, 2013, 33(10): 59-62, 73.

ZENG Ming, LI Na, WANG Tao, et al. Load forecasting compatible with demand-side resources[J]. Electric Power Automation Equipment, 2013, 33(10): 59-62, 73.

[5] 任炳俐, 张振高, 王学军, 等. 基于用电采集数据的需求响应削峰潜力评估方法[J]. 电力建设, 2016, 37(11): 64-70.

REN Bingli, ZHANG Zhengao, WANG Xuejun, et al. Assessment method of demand response peak shaving potential based on metered load data[J]. Electric Power Construction, 2016, 37(11): 64-70.

[6] 潘璠, 贾文昭, 许柏婷, 等. 广东电网需求侧响应潜力分析[J]. 中国电力, 2011, 44(12): 21-25.

PAN Fan, JIA Wenzhao, XU Baiting, et al. Analysis on demandside response potential of Guangdong power grid[J]. Electric Power, 2011, 44(12): 21-25.

[7] 李童佳, 张晶, 祁兵. 居民用户需求响应业务模型研究[J]. 电网技术, 2015, 39(10): 2719-2724.

LI Tongjia, ZHANG Jing, QI Bing. Studies on business model of demand response for residential users[J]. Power System Technology, 2015, 39(10): 2719-2724.

[8] 鞠立伟, 于超, 谭忠富. 计及需求响应的风电储能两阶段调度优化模型及求解算法[J]. 电网技术, 2015, 39(5): 1287-1293.

JU Liwei, YU Chao, TAN Zhongfu. A two-stage scheduling optimization model and corresponding solving algorithm for power grid containing wind farm and energy storage system considering demand response[J]. Power System Technology, 2015, 39(5): 1287-1293.

[9] 姚建国, 杨胜春, 王珂, 等. 平衡风功率波动的需求响应调度框架与策略设计[J]. 电力系统自动化, 2014, 38(9): 85-92.

YAO Jianguo, YANG Shengchun, WANG Ke, et al. Scheduling framework and strategy design of demand response of balancing wind power fluctuation[J]．Automation of Electric Power Systems, 2014, 38(9): 85-92.

[10] United States Department of Energy Office of Electric Transmission and Distribution. “Grid 2030” a national vision for electricity’s second 100 years[Z]. 2003.

[11] VAN A J M, KLEINGELD M, MARAIS J H. Investigating demand response potential in a mining group[C]//2013 Proceedings of the 10th Industrial and Commercial Use of Energy Conference(ICUE). Cape Town: IEEE, 2013: 1-5.

[12] ASANO H, TAKAHASHI M, YMAGUCHI N. Market potential and development of automated demand response system[C]//2011 IEEE Power and Energy Society General Meeting. San Diego: IEEE, 2011: 1-4.

[13] GHAEMI S, SCHNEIDER S. Potential analysis of residential Demand Response using GridLAB-D[C]//IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society. Vienna: IEEE, 2013: 8039-8045.

[14] 李怡静, 方八零, 黎灿兵, 等. 负荷时间弹性及其衡量方法[J]. 电力需求侧管理, 2014, 16(2): 16-20.

LI Yijing, FANG Baling, LI Canbing, et al. The time elasticity of electric load and its identification methods[J]. Power Demand Side Managememt, 2014, 16(2): 16-20.

[15] 孔祥玉, 杨群, 穆云飞, 等. 分时电价环境下用户负荷需求响应分析方法[J]. 电力系统及其自动化学报, 2015, 27(10): 75-80.

KONG Xiangyu, YANG Qun, MU Yunfei, et al. Analysis method for customers demand response in time of using price[J]. Proceedings of the CSU-EPSA, 2015, 27(10): 75-80.

[16] KHAJAVI P, MONSEF H, ABNIKI H. Load profile reformation through demand response programs using Smart Grid[C]//2010 Modern Electric Power Systems. Wroclaw: IEEE, 2010: 1-6.

[17] 阮文骏, 王蓓蓓, 李扬, 等. 峰谷分时电价下的用户响应行为研究[J]. 电网技术, 2012, 36(7): 86-93.

RUAN Wenjun, WANG Beibei, LI Yang, et al. Customer response behavior in time-of-use price[J]. Power System Technology, 2012, 36(7): 86-93.

[18] 张璨, 王蓓蓓, 李扬. 典型行业用户需求响应行为研究[J]. 华东电力, 2012, 40(10): 1701-1705.

ZHANG Can, WANG Beibei, LI Yang. Demand response behavior of typical industrial users[J]. East China Electric Power, 2012, 40(10): 1701-1705.

2017-05-24

王媛(1992)，女，硕士研究生，主要研究方向为电力市场、需求响应、负荷预测等；

周明(1967)，女，教授，博士生导师，主要研究方向为新能源电力系统分析与优化运行、电力市场、需求响应等。

(编辑 刘文莹)

DemandResponsePotentialEvaluationMethodofTime-of-usePriceforResidentialCommunity

WANG Yuan, ZHOU Ming

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)

To adapt to the development of smart grid and promote the reasonable utilization of demand side resources, based on time-of-use price, this paper selects the residential area users as the research object and proposes indexes and a comprehensive evaluation method to describe its demand response potential from time scale. The evaluation indexes define the demand response potential of user in per time period from the aspects of demand response ability and speed. Demand response ability is calculated by applying the conception of demand elasticity matrix of electricity price which is commonly used in economics. Finally, an evaluation model of comprehensive demand response potential in residential area under time-of-use electricity price is established. This method quantifies the demand response potential of the residential area, and provides the basis for the management of the residents’ demand side resources. In the meantime, the results can instruct the formulation of the time-of-use price from the aspects of price setting and peak period division. The analysis of the cases has proved the rationality of the proposed indexes, as well as the validity and universality of the evaluation method.

demand response potential; time-of-use price; price elasticity matrix; climbing rate; evaluation

国家自然科学基金项目(51577061); 国家重点研发计划项目课题(2016YFB0901101)

Project supported by National Natural Science Foundation of China(51577061)；National Key Research and Development Program of China(2016YFB0901101)

TM73

A

1000-7229(2017)11-0048-07

10.3969/j.issn.1000-7229.2017.11.007