初中数学“错误”资源的挖掘与利用
2017-11-27吴忠妙
■吴忠妙
初中数学“错误”资源的挖掘与利用
■吴忠妙
在学生学习数学的过程中,经常会出现教师意想不到的错误,有一些错误易被忽略,不少错误也会在学生的作业和考试中反复出现。此情此景,教师会认为学生没有用心听,没认真反思、订正,甚至会急功近利地指责学生“不开窍”,但静下心来,透过这个现象,是否也要找找我们教师自身的原因呢?是否在教学设计、教学过程等环节出了问题?是否可将学生在学习数学的各个环节中出现的“通病”合理利用呢?笔者也一直在尝试、积累、反思,取得了较好的效果,现举几处学生犯的“错误”,谈谈笔者的心得。
一、利用错误,挖掘学生的探究因子。在每节数学课的相关环节,我都会精心设计与所学新知相关联的素材,这些素材中一部分是学生作业、考试中的常见错误,有一部分是笔者从教材或课外学习材料中提炼设计的“陷阱”,利用孩子的天性,充分调动他们的探究积极性。这些教学资源来源于生活实际或是学生平时学习中易犯的错误,故更有说服力,让学生在找错、纠错的过程中强化了对知识的理解,培养应用数学的意识和良好的数学思维品质。
教学案例一:9.1“反比例函数”的教学片段。
实际问题:无锡到南京的路程大约是200km,一列火车的速度是vkm/h,从无锡到南京所用时间为th。
师:我和南京有着不解之缘,30年前,家人带我从无锡坐火车去南京,不过那时火车的速度只有50km/h,请问需用多长时间?
生:4h。
师:15年前,我在南京读大学时,火车速度大约是80km/h,从无锡到南京坐火车需用多长时间?
生:2.5h。
师:上周我坐高铁去南京,速度达到了250km/h。
生:哇……只有0.8h呀!(边答边填表格)
师:t是v的函数吗?
生:是的。
师:你还能举出生活中类似存在这种数量关系的实例吗?
生:……
师:这些函数关系式的形式有何特征?(小组交流,合作探究。)
学生甲:因变量y随着自变量x的增大而减小。
师:你是从两个变量之间的对应变化关系上分析的,切入点选得很好,但刚才我们所列举的都是实际问题,使用数据都是正数,容易造成错觉,通过后面知识的学习,我们就会知道这两个变量之间的关系并不那么“单纯”,这为以后学习反比例函数的性质埋下了很好的伏笔。
分析与反思:此处学生以偏概全地概括出反比例函数的增减性,由于是实际问题,很容易将自变量的范围定为正数。每一个错误,都能折射出隐藏的思维问题:有的审题不清,忽略或错误理解题意;有的是顺着前面的思路,没有求异思维;有的是概念混淆,理解不深刻。合理利用学生“自创的错误”,以此为突破点,充分挖掘“问题所在”,这也是一种突破教学重点、难点的好点子。
二、利用错误,培养学生的创造意识。在学生学习新知识时,脑海里往往已经储存了不少对旧知识错误或片面的认识,若对学生的这些问题置之不理的话,则会影响对新知的认识、理解、应用。为解决此类问题,笔者借助以前学生学习同类知识时最容易出现的错误,通过“设疑自探—解疑合探—质疑再探”,让学生在自我反思中发现问题,在小组讨论中体现自身思维的价值,通过同伴帮助,教师点拨,完善对知识的理解,学生的质疑创造意识逐渐建立起来。
教学案例二:“勾股定理”教学片段。
师:请思考Rt△ABC中,∠A,∠B,∠C分别对应边a,b,c,若a=3,b=4,求c。
生:c=5,勾三股四弦五嘛。
师:反应很快,勾股定理是对于直角三角形而言的。c=5就是根据勾股数得到的吗?
生:根据∠C=90°。
师:很好,抓住了本质——直角。
生:但不一定是∠C=90°,题目中没有说明,无法确定哪个角是直角。
师:不确定怎么办?
生:分情况讨论,若∠C=90°,则c=5; 若∠B=90°,则不可能是直角,因为它所对的边a不可能是最大边。
师:这种思想方法还在学习哪些内容时用过?
生:等腰三角形的存在性问题,全等三角形的对应关系不确定时……
分析与反思:此处错误是学生思维不严密所致,在不明确哪个角是直角的情况下,应分情况讨论,分类思想是很重要的数学思想,让他们多“掉陷阱”,学生对此会理解得更深刻。学生犯错误的过程,是教育的最好契机;让学生通过纠错,完善思维方法,提升了自身的数学基本素养,并让学生在纠错中获取进一步学好数学的自信,甚至能从中发现一些有价值的数学思想方法。
三、利用错误,培养学生的生成意识。如何突破本节数学课的教学难点时,我总是“绞尽脑汁”,当然课堂中会出现预设的“错误”,也会有一些“突发事件”,若教师采用教学智慧,合理利用,会达到“山重水复疑无路,柳暗花明又一村”的效果。
教学案例三:“轴对称图形”教学片段
师:如下图,四边形ABCD中,AB=AD,∠ADC=∠ABC,问CD=BC吗?请大家思考后再讨论。
学生甲:根据原图,没办法使用条件直接证明,由轴对称想到连接AC,可通过证△ADC≌△ABC得到。
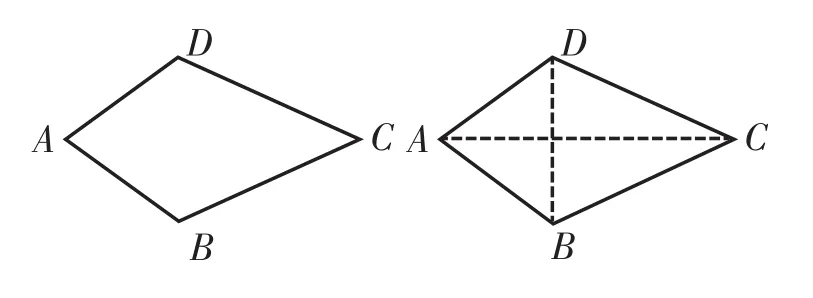
师:很好,从图形的特征想到连接AC,不仅构造了两个三角形且为全等创造了一对等边,真是“一箭双雕”。
学生乙:有问题,“边边角”是不能证两三角形全等的,太想当然了。
师:嗯,学生甲虽然在证全等三角形方法上出了状况,但你有尝试改变现状的勇气。CD≠BC吗?怎么回事?题目有问题呀?
学生丙:题目没问题,若连接BD,由AB=AD,得∠ADB=∠ABD,又因为∠ADC=∠ABC,得∠CDB=∠CBD,由等角对等边得CD=CB。
师:刚才该同学构造了等腰三角形解决了问题。有时一种思路行不通,那就得改变策略,当然要结合所学知识。若连接AC,BD,你还能得出哪些结论呢?
生:……
分析与反思:学生甲由对称很自然地想到连接AC,但不能通过证明三角形全等来解决问题,教师并没有急于否定,而是肯定了他的尝试,通过学生间的互相补充,问题得到圆满解决,并作了相应的拓展。教学的节奏应“正中”学生发展需要的“下怀”,当然也要该出手时就出手,不直接给出结果,多鼓励学生思考,争取有更多的课堂生成。对于那些学习暂时落后的学生,请给他们更多的时间去慢慢思索,慢慢自己调整问题,让他们相信自己能学好数学。
四、利用错误,提升学生的反思能力。在布置作业时,根据以前学生作业或考试中经常出现的易错题,适当地设计一些“陷阱”题,进一步促进学生通过“错误”强化对数学概念或性质的理解,达到“吃一堑长一智”的目的。
教学案例四:讲评易错题
关于x的一元二次方程ax2-(3a+1)x+2(a+1)=0,有两个不相等的实数根x1,x2且有x1-x1x2+x2=1-a,求a的值。(给出以下解法,让学生辨析,学生有说对的,有说错的。)
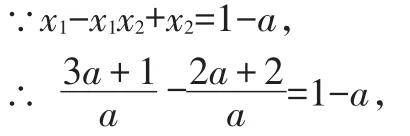
解得a=1或-1。
这题在笔者所教的班级里,约有65%的同学是这样做的,经过再次深入地思考后,学生提出以下想法:
学生甲:对所得结果要检验,当a=1时,原方程根的判别式△=0,此时原方程有两个相等的实数根,故不符合题意,应舍去。
学生乙:由题意得,原方程的根的判别式△>0,先求出△的范围,就会避免以上错误。
师:想想你们出现这类错误的原因是什么?
生:没注意一元二次方程的概念,即a≠0(当然本题没体现出来),还要准确理解一元二次方程根的判别式,思维不严谨……
分析与反思:此处错误是学生常见的错误,一元二次方程有两根的前提是a≠0且△>0,多强调,让学生抓住问题的实质。教师应再认真分析学生产生错误的原因,讲清原委,让学生再练习,再思考,再反思,以后遇到类似的问题,养成检验的习惯,避免掉进“陷阱”,让学生的思维更严谨,解题习惯更具科学性。
实践表明,让学生经历犯错、找错、纠错、感悟提升,这样的学习过程才是完整的。教师有预设性地设置一些障碍,利用学生本身具有喜欢找错误的特点,吸引其眼球,让其探究、思考,放手让“小马”自己摸索过河,自己纠错之后的快乐才是真快乐!
数学错误资源的挖掘和利用是一种教学手段,也是师生在教学活动中进行交流合作的一座桥梁。用心寻找这些“错误”并归纳分类,合理利用这些“错误”,能让教师站在学生角度思考问题,设计教学环节,从而拉近了师生距离,使学生产生更加深刻的认同感。
“错误”亦是一种资源,若教师能合理开发,甚至是创新性地重组、升华,必能达到“别有洞天”的教学境界。
(作者为江苏省江阴市英桥国际学校教师)
