用好相同元素 促进学习迁移——“二次函数的应用（1）”的教学与思考

■吴春兰

用好相同元素 促进学习迁移
——“二次函数的应用（1）”的教学与思考

■吴春兰

很多数学知识之间都具有一定的逻辑关系，或者存在一定的相同元素，因此，在学习新知识时，从原有的知识结构中提取与新知识联系最紧密的知识，让新、旧知识在头脑中发生积极地相互作用，新的知识就能更好地融入学习者原有的知识结构中，并形成新的知识结构，同时新知识还能够对旧知识产生影响。本文以北师大版九年级下册“二次函数的应用（1）”为例，谈谈迁移在教学中的运用，以及它对学生数学学习的影响。

一、教学设计

1.教学背景。

教材内容分析 二次函数是描述变量之间关系的重要数学模型，本课内容是在学生学习了二次函数图像、性质后展开的后续学习，也可为探索二次函数与一元二次方程的关系奠定基础。其重点是让学生从实际问题中建立二次函数模型，并利用二次函数的最值解决实际问题，如以最大利润为代表的问题，提升学生发现问题、提出问题的能力，发展数学模型思想。

学情分析 通过北师大版九上第二章“一元二次方程”的学习，学生已经掌握了列一元二次方程解应用题的方法，大部分学生能够熟练将利润类型的应用题通过建立方程模型求解，但仍有一部分学生暂时不能理清利润问题的数量关系。另外，通过二次函数图像性质的学习，学生已经具备求二次函数最值问题的能力，能够根据图形对变量的变化情况进行初步讨论。

2.教学目标及教学重、难点。

教学目标 能够将实际问题转化为数学问题，建立二次函数模型，明确二次函数表达式的最值与实际问题的最值对应关系。在迁移学习中体验数学的整体性，体会模型思想，增强学好数学的信心。

教学重点 建立二次函数最大利润问题的数学模型，并求出实际问题的最大值。

教学难点 正确理解题意，从实际问题中抽象出二次函数最大利润问题的数学模型。

3.教学流程。

（1）回顾问题，激发迁移。

情境：某商店购进一批单价为20元的日用品，如果以单价30元销售，那么一个月内可售出400件。根据销售经验，提高单价会导致销售量减少。即销售单价每提高1元，销售量相应减少20件。设每件单价提高x元，

问题①：要想每月获得利润4500元，根据题意可列方程：___________________________.

问题②：要想每月获得利润4420元，根据题意可列方程：____________________________.

问题③：要想每月获得利润4180元，根据题意可列方程：___________________________.

问题④：通过以上问题，请说说你发现了什么？

设计意图：复习用一元二次方程解决以利润为代表的应用题，并在此过程中突破“当销售单价变化时，销量与单价之间的关系”这个难点，感受总利润与单价之间的函数关系。设计连续三个具有相同元素的重叠问题，增大迁移量，帮助学生实现从方程模型到函数模型的迁移。

（2）引入函数，实现迁移。

问题⑤：假设你是该商店的老板，从尽量获取利润的角度出发，你会做些什么？

设计意图：从具体利润抽象出变量利润，并实现利润问题最值与函数最值之间的对应关系；体会二次函数是解决一类最优化问题的数学模型，感受数学在现实生活中的运用。根据问题④建立的总利润与提价之间的模型（30+x-20）×（400-20x）=y，自然将方程模型迁移成函数模型，同时理解二次函数最值与实际问题中最大利润的联系。

（3）当堂练习，巩固迁移。

练习：某商店购进一批单价为8元的商品，如果以单价10元销售，那么每天可销售100件。经调查发现，这种商品每提高1元，销售量相应减少10件。

①将销售价提高多少元，可使每天所获利润为320元；

②将销售价提高多少元，才能使每天所获利润最大？最大为多少？

③由于供货量不足，采用限量供应的办法，每天供应50件，要想获得最大利润，应将价格提高多少，才能使每天所获利润最大，最大为多少？

④若要每天所获利润不低于350元，该商品单价的取值范围是多少？

设计意图：问题①②为基础题，面向全体学生；问题③④是面向中上层学生，要求学生结合二次函数图像性质分析自变量的取值范围对函数最值的影响，体会实际生活中种种条件的限制，培养学生的数学应用意识。

（4）新旧对比，感悟迁移。

提升：通过引例和练习，对比方程应用题和函数应用题，你能发现什么？

设计意图：学生通过上两个环节的学习，对比两种应用题的相同元素可得：当利润是具体的数值时，应建立方程类应用题模型，知识结构图如图1；当所求的利润是最值时，应建立函数关系模型，知识结构图如图2。

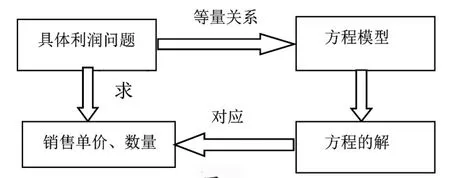
图1

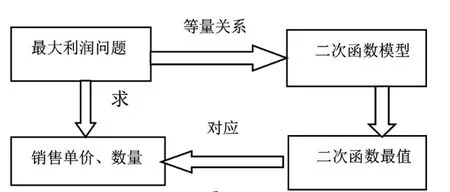
图2

（5）分层作业，巩固知识。

作业：某果园有100棵橙子树，每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。

①如果想要果园橙子总产量是60300个，应该增种多少棵橙子树？

②如果想要果园橙子总产量最大，应该增种多少棵橙子树？

③果园增种多少棵果树，可以使得橙子的总产量在60400个以上？

设计意图：问题①②③综合了列一元二次方程解应用题、二次函数最值应用题、受自变量取值范围影响的二次函数最值问题。巩固不同层次的学生的学习效果。

二、几点思考

1.基于学习认知规律，巧用认知迁移。

心理学研究表明，越是具有普遍意义的知识，越容易保持和迁移。函数学习的普遍性、系统性特征是很突出的，在教学中要基于认知规律，抓住知识的内在相同元素，找准学情，巧妙地把方程的知识迁移到函数问题中，同时把函数问题具体化为方程问题，能够相互促进和补充，对数学学习能起事半功倍的效果。

就本节课而言，列一元二次方程解应用题是学生原有、熟悉的知识，而二次函数的最值问题是新的内容，但是二者的思考方法、技能训练有相当大的重叠。在教学中，把一元二次方程应用题的解题思路、方法迁移到函数应用题中，同时把函数应用题化为方程应用题，是对学习方法的提升。对于解题方法、技能的迁移，从抽象到具体，总结成两个知识结构图，强化学习迁移，也深化了学生对学习迁移的形象理解，从数学解题方法上实现数的理解与形的认知相融合。

2.把握前后联系，实现模型迁移。

笔者曾尝试过在两个班级中对本课时进行与教科书相同步骤的教学，即将二次函数应用题直接抛给学生，让学生经过思考、讨论后，形成解题思路，然后教师分析讲解，帮助学生总结提升。在此传统教学方法下，优秀的学生能通过重新建构函数模型知识结构，把握最值问题的解题方法。有一部分基础一般的学生，也会生搬硬套解题套路。比如设未知数的典型错误是，“设价格提升x元/件，最大利润为y元”，这未能理解题意中“总利润、销售单价同时作为变量”的关系，照搬数学模型进行答题。甚至出现部分学生不设利润y元，因为他们可以理解成一个未知数，或者两个平行的未知数关系（二元一次方程组解应用题），但很难掌握两个变量的二次函数模型。而采用本课时学习迁移的教学策略后，没有一个学生出现生搬硬套数学模型的问题，更可喜的是只要学生能够解方程问题，就可以理解总利润也是一个变量，两者之间是一种二次函数的数量关系，从而能够正确建立最值问题的函数模型。把握前后联系，重视知识的整体教学效果在此较为显著。

3.用好相同元素，完善结构迁移。

学习迁移有赖于情境之间的相同元素。在教学中找准学情，引导学生将已有的知识结构迁移到新的知识结构中，同时让新的知识有效增强对旧知识的理解，归纳新旧知识中的共同的元素，促进新旧知识的交互作用，有利于完善学生的认知结构。

事实上，数学学习方法的渗透是一项长期工程，我们不能希望仅仅通过一节课就能使学生掌握学习迁移，就能完善学生的认知结构，而是应该让学习迁移贯穿在每一块具有相同元素的知识体系中，引导学生用好知识版块中的相同元素，建立完整的知识结构，形成整体化的数学观。在初中数学里，二元一次方程组与一次函数，分式的意义与分式方程解的存在性，一元二次方程与二次函数，全等三角形与相似三角形的性质判定等，它们之间都存在内在的联系，教学中我们都可以采用行之有效的办法，巧用结构性迁移规律，提高学生学习效率。

（作者为广东省深圳市民治中学教师）