一种基于CMA-ES的制导工具误差分离方法研究

2017-11-25韩成柱张志国

航天控制 2017年4期

关键词：外差系统误差遥测

韩成柱梁红张志国

91550部队，大连116023

一种基于CMA-ES的制导工具误差分离方法研究

韩成柱梁红张志国

91550部队，大连116023

为提高制导工具误差线性模型求解精度，基于优化模型，利用进化策略方法实现了对制导工具误差线性模型的求解，并研究了遥、外测数据随机误差对制导工具误差线性模型求解精度的影响。仿真结果表明，该方法优于主成分法，制导工具系统误差系数估计值与仿真均值之差均比标准差小3倍，遥测数据随机误差对环境函数的影响较小，遥外差数据随机误差对线性模型求解精度影响较大，制导工具系统误差的最大偏离真值量比标准差大1倍。

误差分离；制导工具系统误差；进化策略

惯性制导系统的精度是飞行器命中精度的最大影响因素。制导系统误差分为方法误差和工具误差，而后者引起的飞行器落点偏差约占总误差的80%左右。实践证明，仅从硬件上提高惯性器件的精度是有限的[1]，而采用误差补偿技术，即从软件上建立精确的、便于分离制导工具系统误差系数的模型，并给出高精度参数估计方法，是提高飞行器精度的关键技术之一。

传统的制导工具系统误差分离方法的基本思路是：建立描述惯性器件的线性、非线性回归模型，然后利用诸如最小二乘方法等参数估计方法解此回归模型[1-2]。对于惯性工具误差模型来说，由于各误差系数项之间的相关性等因素，使得设计矩阵条件数巨大，虽可采用有偏估计方法，提高参数估计的精度，但效果仍不理想。

徐德坤[3]和蒋小勇[4]另辟蹊径，避开环境函数求逆，将线性回归问题转化为一个目标函数求极值问题，从而利用进化策略寻优方法分离误差系数，得到了较好的结果，但它们都没有进行模型优化。本文将在优化模型的基础上，研究遥、外测数据随机误差对进化策略误差分离结果的影响，并与主成分法[1](非线性回归模型参数的有偏估计方法)进行了比较，结果表明CMA-ES法所得结果要优于主成分法。

1 进化策略的误差分离方法

1.1 制导工具系统误差系数分离的模型

制导工具系统误差系数分离的线性模型可描述为：

ΔW=SC+ε

(1)

其中，ΔW为3n×1维惯性系下遥外差观测向量；C为m×1维待分离的误差系数向量；S为与C对应的3n×m维环境函数矩阵；ε为3n×1维观察误差，为白噪声；n为观测采样点个数，m为制导工具系统误差项数，且3ngt;m。

为能应用于进化策略算法，此线性回归模型可改写为如下优化模型：

(2)

其中，var(ΔW)为遥外差数据方差；g(C)为系统约束函数。

1.2 进化策略

进化策略算法中，其个体中含有随机扰动因素，且以个体的变异运算为主要搜索技术，因而具有快而强的全局优化能力[3-8]。为优化设置进化策略自身参数，N.Hansen[7]引入一种协方差矩阵自适应进化策略(Covariance Matrix Adaptation Evolution Stragety,CMA-ES)。CMA-ES主要基于突变因子分布的自适应机制实现进化策略参数优化调整，使随机生成的初始解通过复制、交换、突变和选择等遗传操作不断的迭代进化，逐步逼近并最终得到最优解[8-11]。

应用CMA-ES进行误差分离基本过程为：

1)初始化种群。初始种群服从正态分布，根据下式初始化种群：

xi～Ni(m,σ2C)=m+σNi(0,C)=m+σzi

(3)

其中，m为均值向量，i为种群规模，σ为步长，C为协方差矩阵，初始化为单位阵。

2)更新均值向量m。根据适应度函数，即残差平方和排序后前h项残差平方和SLTS，计算当代种群中每个个体的适应度值并排序，选择最优子群根据下式赋值(子群规模u一般为种群规模的0.3倍)：

(4)

其中，wi为权重，适应度函数小的取最大权重，zi:λ是服从正态分布的随机数。

3)更新协方差矩阵C

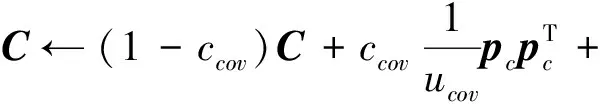
(5)

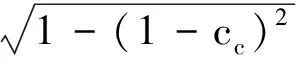
(6)

其中，ccov≈2/n2，cc≈4/n，n为维度，ueff为待分离的工具误差系数，其中ueff≈0.3λ，ccov≈ueff/n2，n2为比例系数，一般取值在2～4之间，ucov=ueff，pc是C的权重差分和。

4)更新步长σ

(7)

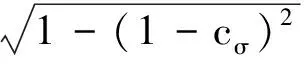
(8)

5)循环过程2)～4)，直到设定的条件，如子代数到达1000代，或两代间的误差到达1×10-6，最优子代即为参数估计解。

1.3 方法的求解流程

根据上述原理，利用CMA-ES即可实现对制导工具系统误差的分离，同时研究遥外测数据质量对求解精度的影响，求解计算流程如图1所示。

图1 求解计算流程图

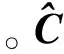
2 影响因素分析

本算例中遥外测线性模型的制导工具误差系数包括24项：C1，C2，…，C24，经过对飞行器纵向、横向落点偏差对误差系数偏导数，误差系数对遥外差数据影响等模型优选方法的分析，误差系数优选为12项：C1，C2，C3，C13，C14，C15，C18，C19，C20，C22，C23和C24。由此可通过改变ε大小来分析遥测数据随机误差对CMA-ES法求解精度的影响，改变η的大小来讨论遥外差数据随机误差对求解精度的影响。

2.1 遥测随机误差对求解精度影响

现将η设置为方差为σ(η)=[0.03m/s，0.03m/s，0.003m/s]的白噪声，改变遥测随机误差ε的方差为[0.05m/s，0.05m/s，0.005m/s]、[0.04m/s，0.04m/s，0.004m/s]和[0.03m/s，0.03m/s，0.003m/s]，优化所得的DB值如图2所示。可以看出，当遥测随机误差的方差增大时，误差系数的估计值基本不变。分析其原因，在此仿真过程中，遥测数据的精度仅影响了环境函数S，而环境函数S是遥测速度和加速度的积分，导致环境函数S的数值量级较遥测数据方差巨大，从而S矩阵变化很小，故误差分离结果不受遥测数据精度的影响。但实际误差分离时，遥测数据的精度还影响了遥外差，从而影响误差分离结果，本节不单独讨论它，而将其并入遥外差数据中，在下节讨论。

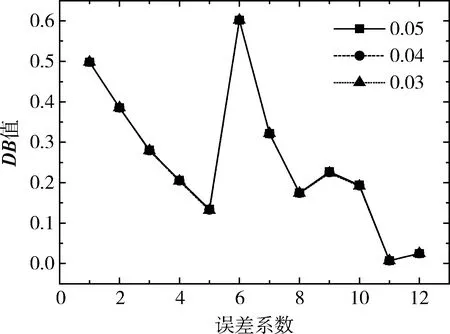
图2 不同遥测随机误差时，各误差系数所对应的DB值

2.2 遥外差数据随机误差对求解精度影响

现设定σ(ε)=[0.03m/s，0.03m/s，0.003m/s]，而改变遥外差数据随机误差方差σ(η)为[0.04m/s，0.04m/s，0.004m/s]、[0.03m/s，0.03m/s，0.003m/s]、[0.02m/s，0.02m/s，0.002m/s]和[0.01m/s，0.01m/s，0.001m/s]，所加随机误差序列相同，幅值不同，从而得到不同方差的白噪声，经CMA-ES求解得到的DB值如图3所示。由图可知，所有DB值均小于3，即所有12项所选误差系数均能很好的分离出来。但随着遥外差数据随机误差的变大，DB值变大，即求解精度变差。且各误差系数的DB值随方差变化幅度不同，显然变化幅度大的误差系数容易导致模型的病态。

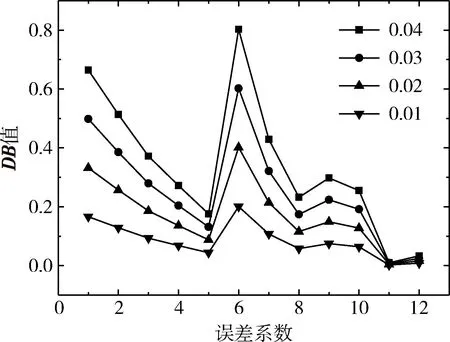
图3 不同遥外测随机误差时，各误差系数所对应的DB值

3 仿真验证及对比

为考查基于优化模型的CMA-ES应用效果，讨论不同白噪声随机序列对求解精度的影响。设σ(ε)=[0.03 m/s，0.03 m/s，0.003 m/s]，σ(η)=[0.02 m/s，0.02 m/s，0.002 m/s]，4组不同随机序列所对应的优化结果如图4所示。可以看出，不同随机序列所对应各DB值变化较大，没有明显的规律，可以理解为生成白噪声序列时，若该白噪声某处的峰值(即数据鼓包)较大时，对应的优化精度较差。故在实际误差分离中，应尽量减小遥外差数据的随机误差、尖峰和鼓包等，使得遥外差数据尽量光滑[12-13]。图5对比了相应随机序列利用主成分法得到的参数估计结果，对比图4，发现主成分法所得DB更大，即CMA-ES法所得结果优于主成分法所得结果。

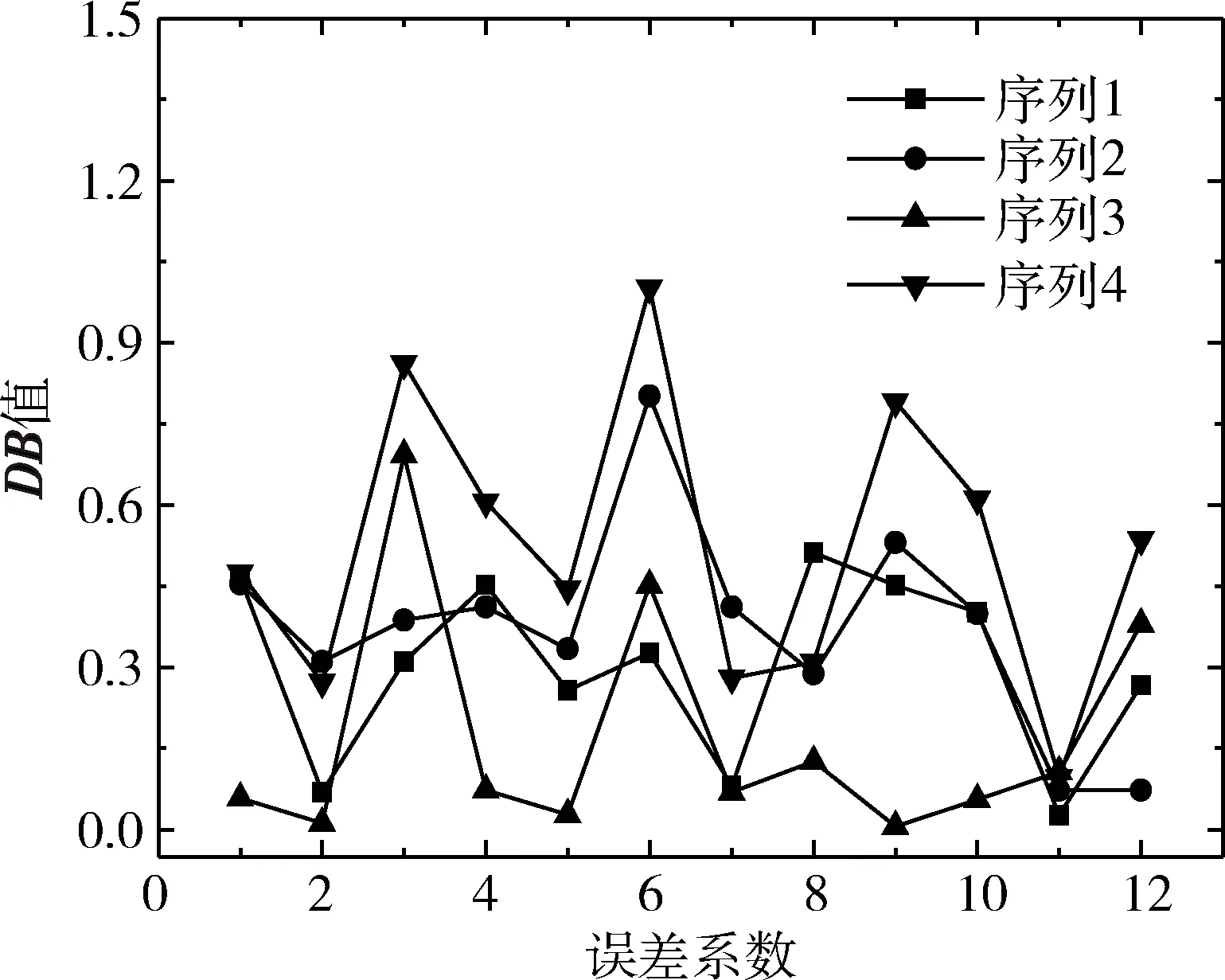
图4 4组不同随机序列对应的误差分离结果

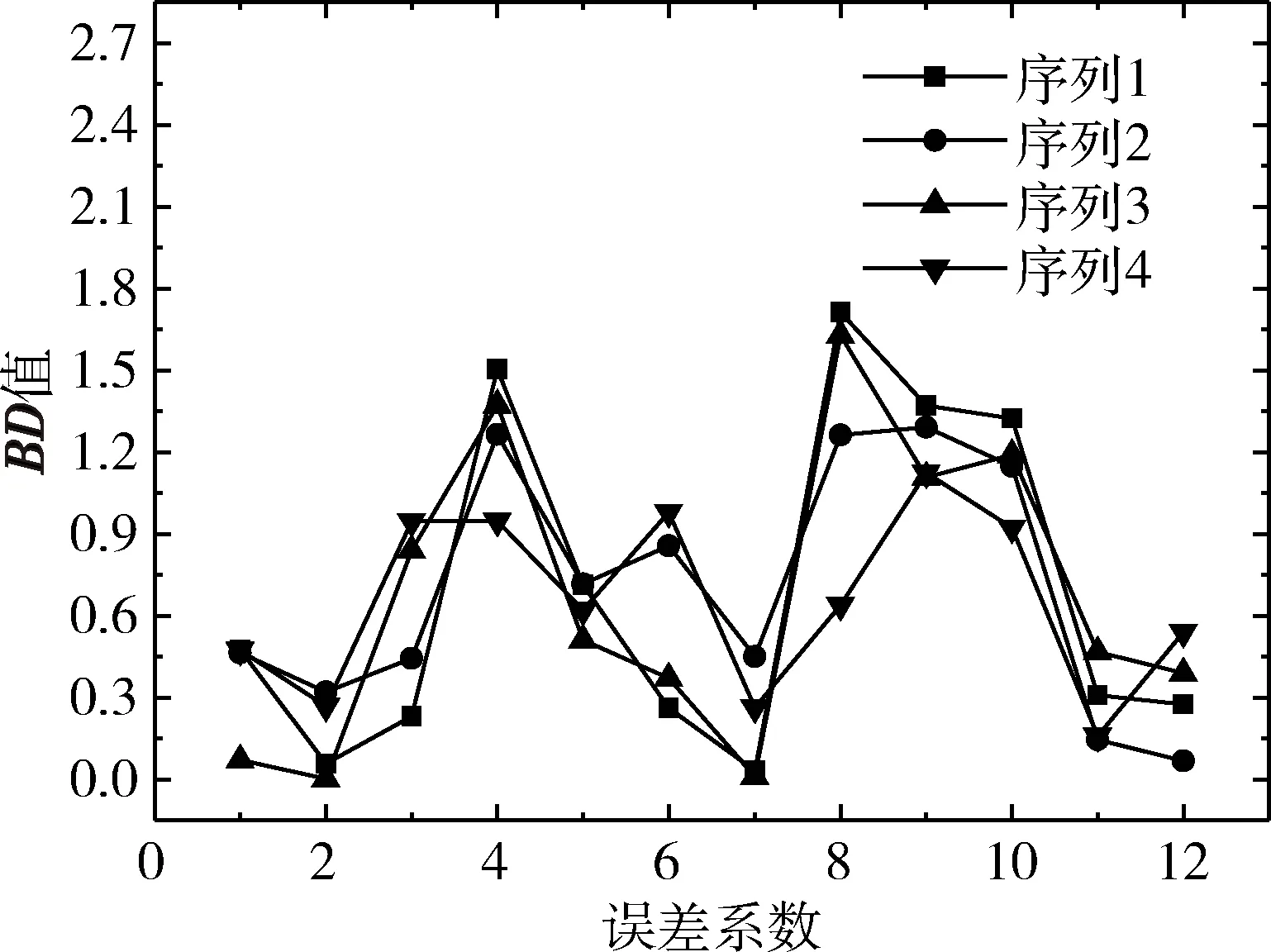
图5 4组不同随机序列利用主成分法误差分离结果

4 结论

利用CMA-ES研究了遥外测数据随机误差对遥外测线性模型求解精度的影响。研究结果表明，遥测数据方差对环境函数的影响较小；而遥外差数据方差对线性模型求解精度影响较大，最大偏离真值达2倍于地面测试标准偏差。故在实际误差分离时，应尽可能使遥外差数据平滑。

[1] 王正明,易东云,周海银.弹道跟踪数据的校准与评估[M]．长沙：国防科技大学出版社，1999: 93-97,328-338.(Wang Zhengming, Yi Dongyun ,Zhou Haiyin. The Calibration and Evaluation of Trajectory Tracking Data [M].Changsha:Press of National University of Defense Technology,1999:93-97,328-338.)

[2] 姚静，段小君，周海银.海态制导工具系统误差建模与参数估计[J].弹道学报，2005，17(1): 33-39.(Yao Jing，Duan Xiaojun,Zhou Haiyin.Modeling and Parameters Estimation of Marine Guidance Instrumentation Systematic Error[J].Journal of Ballistics,2005,17(1):33-39.)

[3] 徐德坤，刘伟，孟云鹤，等.基于进化策略的误差分离方法[J].宇航学报，2008，29(1):352-356.(Xu Dekun，Liu Wei，Meng Yunhe, et al.Evolutionary Strategies Based Error Sepration Method[J].Journal of Astronautic,2008,29(1):352-356.)

[4] 蒋小勇，孟云鹤，郑伟.基于进化策略的潜射弹道导弹弹艇误差分离技术研究[C].第24届飞行力学与飞行试验学术交流年会论文集, 2008,9：205-210.(Jiang Xiaoyong,Meng Yunhe ,Zheng Wei .Research on Separation of Missile and Submarine-launched Ballistic Missile[C]. The Twenty-fourth Session of China Flight Dynamics and Trial Conference,2008,9:205-210.)

[5] SKeerthi S S. Efficient Tuning of SVM Hyper Parameters Using Radius//Margin Bound and Iterative Algorithms[J]. IEEE TransNeuralNet-works, 2002, 13(5): 1225-1229.

[6] Kaibo Duan, S Sathiya Keerth,Aun Neow Poo. Evaluation of Simple Performance Measures for Tuning SVM Hyperparameters [J].Neuro Computing, 2003, 51: 41-59.

[7] Nikolaus Hansen. The CMA Evolution Strategy:A Comparing Review[C ].Towards a New Evolutionary Computation. Berlin:Springer, 2006：75-102.

[8] Hansen N,Ostermeier A.Completely Derandomized Self-adaptation in Evolution Strategies[J]. Evol Comput, 45,159-195, 2001.

[9] Nikolaus Hansen,Andreas Ostermeier. Completely Derandomized Self-adaptation In Evolution Strategies[J]. Evolutionary Computation,2001, 9(2): 159-195.

[10] J Platt. Fast Training of Support Vectormachines Using Sequential Minimal Optimization[M]. Advances in Kernel Methods-Support VectorLearning. Cambridge, MA:MIT Press,1999：185-208.

[11] Chang Chihchung,Lin Chihjen.LIBSVM:a Library for Support Vector Machines (Version 2·88)[R].Department of Computer Science and Information Engineering, National Taiwan University, Taipe, Taiwan, 2008.

[12] Runarsson T P,Yao X. Stochastic Ranking for Constrained Evolutionary Optimization[J]. IEEE Transactions on Evolutionary Computation, 2000,4(3):284-294.

[13] Runarsson T P,Yao X. Search Biases in Constrained Evolutionary Optimization[J]. IEEE Transactions on System, Man, and Cybernetics: Part C,X,No.XX, Month 2004(SMCC KE-09).

ResearchoftheGuidanceInstrumentErrorSeparationBasedontheCMA-ES

Han Chengzhu， Liang Hong， Zhang Zhiguo

Unit 91550 PLA, Dalian 116023, China

Theevolutionarystrategiesmethodbasedontheoptimizationmodelisusedinsolvingtheguidanceinstrumenterrorslinearmodel.Andtheeffectoftherandomerrorofthetrackingandtelemetrydatatosolvetheguidanceinstrumenterrorlinearmodelisstudied.Thesimulationresultsshowthatthismethodisbetterthanprinciplecomponentanalysismethod,thedifferencebetweentheestimationvalueandthesimulationmeanvalueofguidancetoolsystemerrorcoefficientislessthan3timesthestandarddeviation,theeffectofthetelemetrydate’srandomerrortoenvironmentalfunctionsissmall,theeffectofthetelemetry-trackingdeviationtosolvetheguidanceinstrumenterrorlinearmodelisbigandthebiggestdifferencebetweentheguidanceinstrumentsystemerrorandthemeanvalueisbiggerthanonetimethestandarddeviation.

Errorseparation;Guidanceinstrumentsystemerrors;Evolutionarystrategies