面向月面遥操作任务规划系统的搜索剪枝策略研究*

2017-11-25蔡敦波

航天控制 2017年4期

关键词：剪枝搜索算法时态

高薇蔡敦波

1.北京航空航天大学宇航学院，北京100083 2.北京航天飞行控制中心, 北京 100094 3.武汉工程大学智能机器人湖北省重点实验室，武汉 430205

面向月面遥操作任务规划系统的搜索剪枝策略研究*

高薇1,2蔡敦波3

1.北京航空航天大学宇航学院，北京100083 2.北京航天飞行控制中心, 北京 100094 3.武汉工程大学智能机器人湖北省重点实验室，武汉 430205

针对月面巡视器任务规划涉及资源变量的特点，从理论上分析了经典的“有利动作”剪枝策略的不足,提出了一种适用于时态规划模型的“资源分析增强型有利动作”剪枝策略。此剪枝策略通过分析“资源变量”与动作效果的关系,计算出被“有利动作”策略忽视的动作,能在裁剪问题空间的同时，提高搜索算法的求解能力。试验结果表明了本文剪枝策略的有效性。

月面遥操作；任务规划；剪枝策略

嫦娥三号任务取得了中国首次在月球上实施巡视器软着陆和巡视勘察的成功[1]。“玉兔号”巡视器与着陆器脱离后，在月面前进实施科学探测任务，每项探测任务均在地面“远程遥操作”的控制方式下完成[2]。地面站对综合巡视器的各项数据进行逻辑抽象，构建“时态规划问题”(Temporal Planning Problem)，调用专门设计的“自动规划系统”进行求解，输出规划方案，上传至巡视器[3]。这种自动地进行任务规划的方法相对于以往人工编制规划的方法在任务完成效率上具有显著优势。

然而，时态规划的计算复杂度一般为EXPSPACE-complete，仅在某些特殊情况下属于难度略低的PSPACE-complete[4]。为设计有效的时态规划算法，学界主要从“搜索算法”和“剪枝策略”2个方向开展研究。在搜索算法方向上，Hoffmann等提出了“增强爬山算法”[5]，Helmert等提出了结合“多优先队列”的贪婪最好优先搜索算法[6]。这些算法与设计良好的启发函数结合，将规划算法的能力提高到了新的水平[7]。在剪枝策略上，Hoffmann等为经典规划模型STRIPS设计的“有利动作”(Helpful Actions，HA)策略[5]，以及Helmert等提出的“有利转移”策略[6]在自动规划领域最先出现，并一直具有重要影响，至今仍是国际先进的规划算法的关键技术[8-10]。

针对“玉兔号”月面巡视器控制任务的新特点，地面控制中心将以往的人工编制工作计划的经验与人工智能领域的自动规划技术结合，设计了具有自动化任务建模和任务规划能力的任务规划系统。采用自动规划领域较成熟的PDDL语言(Planning Domain Definition Language)[3-4]进行了任务建模和基于“状态空间搜索”的规划求解。在进行规划解搜索的过程中，因为时态规划的计算复杂度是EXPSPACE-complete，对应的问题空间规模较大，所以为了使搜索算法专注于问题空间中含有目标状态的部分，需要有效的剪枝策略。针对时态规划模型，本文扩展了Hoffmann等为经典规划模型STRIPS设计的剪枝策略HA，分析了HA在时态规划模型上的不适用性，提出了一种改进的剪枝策略“资源分析增强型有利动作”(Resource Analysis Enhanced Helpful Actions，RAEHA)。在规划系统Sapa[11]上实现了RAEHA，通过实验验证了RAEHA的有效性。

1 基本概念

1.1 月面巡视器任务规划与时态规划

月面巡视器任务规划是在给定初始条件(包括月表环境条件和巡视器自身状态)、操作约束集以及目标集合(包括目标位置、到达目标位置时的巡视器状态及时间等)的前提下，事先规划出巡视器的月面行使路线，安排在该路线上的行为(动作)序列(如充电、拍照等)。该规划使月面巡视器能按要求到达目标状态，且行进过程满足相关的操作约束。巡视器任务规划问题被抽象为“时态规划问题”。

定义1 时态规划问题(Temporal Planning, TP)表示为∏=(V,A,I,G,TL,δ)，其中：

1)V由2个不相交的有限变量集组成：VL∪VM，变量的取值随时间而变化。VL是(逻辑)命题变量集，l∈VL的值域为Dom(l)={T,F}；VM是数值变量集，m∈VM有值域Dom(m)⊆R；

2)A是动作集：动作a∈A具有形式〈da,Ca,Ea〉，da表示动作的持续时间；Ca是a的执行条件集合(简称：条件集)，描述在动作执行过程中必须成立的条件；Ea是a的执行效果集合(简称：效果集)，包含动作a在开始执行时刻产生的效果和结束时刻产生的效果。对于条件c∈Ca，如果它约束逻辑变量，则具有形式〈(sc,ec)v=r〉，r∈Dom(v)，sc和ec分别为条件“v=r”应成立的“开始时刻”和“结束时刻”；如果它约束数值变量，则有形式〈(sc,ec〉voxgt;，o∈{gt;, ≥ , lt;, ≤, =}是比较算符，x是由数值变量和常量组成的数学表达式。对于效果f∈Ea，如果它影响逻辑变量，则具有形式〈[t]v←r〉；如果影响数值变量，则有形式〈[t]vo′x〉，o′∈{=,+=, -=, *=, /=}；

3)I是规划任务的初始状态，它为l∈VL赋予真值“T”或“F”，为m∈VM赋予r∈Dom(m)；

4)G是目标集，其中每个目标命题具有形式〈v=r〉，其中v∈V，这些目标在规划方案执行后必须成立；

5)TL是“定时触发文字”的有限集，其中每个(命题)文字的形式为〈[t]v=r〉，表示变量v∈V在时刻t的取值更新为r；

6)δ:A→R是动作的代价函数，表示执行a需要付出代价，δ(a)lt;0表示执行a获得收益。

对动作的时间语义进一步说明如下。将动作a的开始执行时刻和结束时刻分别记为sa和ea。对于动作执行条件c∈Ca，如果sc=ec=sa,则要求条件c在a的开始时刻成立，称此类条件为“开始条件”；如果sc=ec=ea,则要求c在a的结束时刻成立，称此类条件为“结束条件”；如果sc=sa,ec=ea,则要求c在开区间(sa,ea)上成立，称此类条件为“持续条件”。对于动作a的效果〈[t]v←r〉，如果t=sa,则该效果在动作的开始时刻发生，称此类效果为“开始效果”；如果t=ea,则该效果在动作的结束时刻发生，称此类效果为“结束效果”。

TP模型中刻画巡视其所处的外部环境变化所使用的技术为“定时触发文字集”(Timed Initial Literals)，即TL集合反映了逻辑变量随外部时间的变化信息。

给定TP问题实例，它的状态s由V中变量的赋值组成。用s(v)表示s对变量v的赋值。状态不一定为全部变量给出赋值：仅为部分变量赋值的状态称为“部分状态”(Partial State)，为所有变量赋值的状态称为“完全状态”(Full State)。

定义2 (动作在状态上的可执行)在状态s上，如果动作a的“开始条件”在时刻sa成立、“结束条件”在时刻ea成立及“持续条件”在开区间(sa,ea)上成立，则称a在s上可执行，记为applicable(a,s)。同时，s上所有可执行的动作记为app_actions(s)={a|a∈A,applicable(a,s)}。

用π=(〈t(a1),a1,da1〉,…, 〈t(am),am,dam〉)表示动作序列，其中变量ai表示在第i步执行的动作，t(ai)表示ai的计划执行时刻。

定义3 (有效动作序列)对于状态s，如果π中的动作可依次执行，则称π为s上的“有效动作序列”。

定义4 如果π为初始状态I上的有效动作序列，并且执行am后的状态满足目标集G的全部目标，则称π为TP问题∏ = (V,A,I,G,TL,EP,δ)的“规划”(Plan)，也称为“规划解”或“规划方案”。

通常一个TP问题的规划解不止一个，记规划解的集合为Solutions(∏)。

下面给出月面巡视器任务规划问题的一个简化实例，以及如何采用TP模型来建模本实例。假定月面上有2个停泊点：A和B，巡视器当前位于A，其任务目标是在B处完成探测工作。巡视器当前能量为80，在相对时刻30开始处于太阳光照区域。任务约束为：在执行探测动作之前，巡视器的能量应gt;50，在探测动作的执行过程中应一直处于太阳光照区域。从A～B的移动持续时间为10、能量消耗为30且要求当前能量gt;40。在B处进行探测动作的持续时间为15、能量消耗为20且要求当前能量大约30。这个规划实例在时间跨度指标上的最优解是：在时刻0执行从A～B的“移动动作”，在时刻30执行“探测动作”。

运用定义1的TP模型，能对上述实例进行建模，具体建模过程如下。设逻辑变量集VL={at_A, at_B, reachable_A_B, in_sun, work_done}。各逻辑变量的含义如下：用T和F表示逻辑“真”和逻辑“假”，at_A = T表示巡视器在停泊点A，at_B=F表示巡视器不在停泊点B，reachable_A_B=T表示停泊点A和B在空间上可达，in_sun=T表示巡视器处于光照范围内，work_done=F表示探测工作未完成。设数值变量集VM={energy}，energy变量建模巡视器的当前电量值，其余2个变量分别表示移动动作和探测动作的电量消耗。初始状态I={at_A=T, at_B=F, reachable_A_B=T, in_sun=F, work_done=F, energy=80}。目标集G={work_done=T}，表示任务目标：要完成探测工作。

巡视器的行为建模如下： A和B两点间的移动动作m=〈10,Cm,Em〉，它的条件集Cm={〈(sm,sm) at_A = T〉, 〈(sm,sm) reachable_A_B=T〉, 〈(sm,sm) energy gt;= 40〉}，它的效果集Em={〈(em,em) at_B = Tgt;, 〈(em,em) at_A = Fgt;, 〈(em,em) energy -= 30〉}。在B点工作的动作w=〈15,Cw,Ew〉，它的条件集Cw={〈(sw,sw) at_B=T〉, 〈(sw,sw) energy gt;=30〉, 〈(sw,sw) work_done = F〉}，它的效果集Ew={〈(ew,ew) energy-=20〉, 〈(ew,ew) work_done=T〉}。 “定时触发文字”集TL={〈[30] in_sun=T〉}表示巡视器在时间30上位于太阳光照内。

可见，月面巡视器任务规划问题涉及函数与数值变量的处理、时态关系的处理及外部事件的处理等多个复杂的方面，对求解算法的效率提出了挑战。

1.2 启发式状态空间搜索与剪枝策略

目前，求解时态规划问题的最有效方法是基于状态空间搜索的方法[10]。其基本搜索过程为：对当前状态s，首先计算s的可用动作集app_actions(s)，然后依据其中的动作生成s的后继状态，再从后继状态中选择一个作为新的当前状态。此过程持续到当前状态满足目标条件为止。当app_actions(s)中含多个动作时，优先选择哪个动作对应的后继状态，受启发函数的引导，因而称为“启发式”状态空间搜索。另一种互补的求解技术是从app_actions(s)中排除不可到达或无希望到达目标状态的动作，这种技术称为“剪枝策略”。因而，启发函数和剪枝策略的有效性成为规划算法求解效率的关键。

2 “有利动作”剪枝策略的性质分析

首先简要介绍Hoffmann等为经典规划模型STRIPS设计的“有利动作”剪枝策略，然后分析该策略在时态规划模型上的不适用性。本节证明了“有利动作”策略在时态规划上导致不完备性。

2.1 “有利动作”剪枝策略

在规划求解的过程中，“有利动作”剪枝策略为每个状态s定义了候选动作集HA(s)，且HA(s)⊆app_actions(s)。HA(s)的计算流程如下：首先，以s为初始状态构建一个“松弛规划图”(Relaxed Planning Graph)[6]；然后，从该图中提取松弛规划解，并根据这个规划解确定在“松弛时态规划图”第1命题层的子目标命题集G1；最后，将添加了命题p∈G1的动作加入到HA(s)，即

(1)

2.2 HA策略可导致的不完备性

如果时态规划搜索算法使用HA作为剪枝策略，即对于每个状态s，只将HA(s)作为扩展状态s的候选动作，而排除集合app_actions(s)- HA(s)中的动作，则算法是不完备的。这将导致某些规划问题采用HA剪枝策略的搜索算法可能无法求解，但实际上该类问题并非无解。这类问题的主要特点是在规划解中存在某个动作，它的动作效果只包含数值变量(资源变量),而不包含逻辑变量。

3 资源分析增强型剪枝策略

针对剪枝策略HA的不足，本文提出一种改进型的剪枝策略RAEHA。改进的思路是根据定理1及其证明过程，在RAEHA中首先定义与实现目标相关的资源变量，然后定义与该资源变量相关的动作，最后将在当前状态上可用的、与资源变量相关的动作定义为有利动作。根据该方式，为当前状态s计算的有利动作集合记为RAEHA(s)。

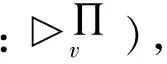
1)∃(v=d)∈G；

2)∃a∈A:〈[x,x′]v=d〉∈Ca

从含义上讲，条件1)定义了在目标条件中直接包含的变量是目标相关的；条件2)定义了与目标间接相关的变量，这种变量出现在某个动作的前提中，而同时该动作的动作效果中含有目标相关的变量。本文仅考虑与目标相关的资源变量，因此进行如下定义。

根据目标相关的资源变量，可以为当前状态s分析得到可用的、通过改变资源而与目标相关的动作集合，如下：

(2)

由式(2)可得，HA(s)⊆RAEHA(s)。

命题1 如果在任务∏的状态s上，存在一个逻辑效果为空,并且与目标相关的动作a，则有HA(s)⊂RAEHA(s)。

在命题1中，HA(s)是RAEHA(s)的真子集的原因在于动作a。一方面，动作a是目标相关的，但因为动作a的逻辑效果为空，所以动作a一定是通过某个资源变量而与目标相关的。由于a是通过某个资源与目标相关，所以根据式(2)的定义，有a∈RAEHA(s)，同时，a∉HA(s)。因此，命题1表明了RAEHA相比HA能收集更多的与目标相关的动作。

命题2 相比于运用HA剪枝策略，运用RAEHA剪枝策略的搜索算法能求解更多的时态规划任务。

命题2的证明过程分为2部分：1)根据命题1，任何一个通过运用HA能求解的问题，运用RAEHA也能求解；2)构造一个简单的规划任务∏′，该规划任务能运用RAEHA策略求解，但它不能用HA求解。任务∏′的具体描述如下：

V=VL∪VM,VL=φ,VM={v}；

A={a}，a=(6,Ca,Ea)；

Ca={([sa,sa]v=3)}；Ea={([ea]v=7)}；

TL=φ；δ(a)=20；

I={(v=3)}；G={(v=7)}。

4 实验与分析

在时态规划系统Sapa的基础上，使用Java语言实现了本文设计的剪枝策略RAEHA。Sapa采用的搜索算法为前向A*算法[11]，针对时态规划模型提出了运用“时态规划图”评估搜索状态的目标距离。该技术在近年来多次用于新型经典规划算法[12]和概率规划算法的设计[13]，因而Sapa是时态规划领域的一个代表系统。

为提高求解效率，Sapa在时态规划模型上对HA剪枝策略进行了扩展，但它未考虑到本文提出的动作与目标在资源上的相关性。然而，在月面巡视器任务规划中，频繁涉及到影响资源的动作，这类动作对Sapa的求解效率提出了挑战。同样的，美国火星巡视器任务规划也涉及资源操作。为对比分析HA和RAEHA对Sapa求解效率的影响，选用了智能规划领域公开的、美国火星巡视器任务规划的问题集“Satellite”[14-15]进行实验和分析。

本实验主要从搜索算法的求解效率受资源相关动作的影响方面分析本文提出的RAEHA策略相对于HA策略的优势。实验环境为CPU 2GHz、内存限制2GB、求解时间7200s，JDK1.8。详细的实验数据如表1所示，其中“-”表示无数据。“Satellite”问题集共包括20个具体的任务，任务名称从prob1到prob20。Sapa在使用完整的求解技术时能够求解如表1所含的11个任务[11]。因此，在这11个任务上分析RAEHA与HA对求解能力和效率的影响。主要得出如下结果：

1)在规划任务prob10上，Sapa使用RAEHA策略能够成功求解，仅在884ms内就得到了一个包含4个资源相关动作的规划解。而它使用HA策略在7200s的时间限制内未能成功求解,表明某些规划任务对应的方案需要资源相关的动作，即，不使用资源相关的动作，可能需要较长的规划解，或者无法形成规划解。因此，RAEHA策略对规划系统的求解能力有本质的提高;

2)在规划任务prob4，prob7和prob8上，结合了RAEHA策略的Sapa分别构造了包含1个、1个和2个资源相关动作的规划解。同时，结合HA策略的Sapa不使用资源相关动作，也同样成功求解。但是，运用RAEHA时，评估的状态数均一致地低于运用HA时的水平。而且，结合RAEHA时，在这3个任务上的总求解时间优于结合HA时的总求解时间，因此可提高求解效率。

以上数据和分析表明，本文提出的搜索剪枝策略RAEHA在工程应用方面对HA策略实现了有效的改进。

5 结论

从原理上分析了智能规划领域有代表性的搜索剪枝策略HA扩展到时态规划后所导致的不完备性。提出了“资源分析增强型有利动作”剪枝策略：RAEHA，并从支持规划算法求解完备性的角度证明了RAEHA优于HA。在开源的Sapa规划系统上实现了RAEHA策略，并使用与我国月面巡视器任务规划相关的美国火星巡视器测试问题集进行了测试，表明了RAEHA在求解能力和求解效率上优于HA。

表1 RAEHA策略与HA策略的对比实验数据

[1] 吴伟仁, 周建亮, 王保丰, 等. 嫦娥三号 “玉兔号” 巡视器遥操作中的关键技术 [J]. 中国科学信息科学 (中文版), 2014, 44(4): 425-440. (Wu Weiren, Zhou Jianliang, Wang Baofeng, et al. Key Technologies in the Teleoperation of Chang′E-3 “Jade Rabbit” Rover[J]. Science in China Series F: In-formation Sciences, 2014, 44(4): 425-440.)

[2] 贾阳, 张建利, 李群智, 等. 嫦娥三号巡视器遥操作系统设计与实现[J]. 中国科学技术科学 (中文版), 2014, 44(5): 470-482. (Jia Yang, Zhang Jianli, Li Qunzhi, et al. Design and Realization for Teleoperation System of the Chang′e-3 Rover[J]. Science in China Series E: Technological Sciences, 2014, 44(5): 470-482.)

[3] 高薇,蔡敦波,周建平,等. 嫦娥三号“玉兔号”巡视器行为规划方法[J]. 北京航空航天大学学报,2017, 43(2): 277-284.(Gao Wei, Cai Dunbo, Zhou Jianping, et al. Activity Planning Method for Chang′E-3 “Jade Rabbit” Rover[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2017, 43(2): 277-284.)

[4] Rintanen J. Complexity of Concurrent Temporal Planning[C]//Proceedings of the Seventeenth International Conference on International Conference on Automated Planning and Scheduling. AAAI Press, 2007: 280-287.

[5] Hoffmann J, Nebel B. The FF Planning System: Fast Plan Generation Through Heuristic Search[J]. Journal of Artificial Intelligence Research, 2001, 14: 253-302.

[6] Richter S, Westphal M. The LAMA Planner: Guiding Cost-based Anytime Planning With Landmarks[J]. Journal of Artificial Intelligence Research, 2010, 39(1): 127-177.

[7] Seipp J, Sievers S, Helmert M, et al. Automatic Configuration of Sequential Planning Portfolios[C]//Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. AAAI Press, 2015: 3364-3370.

[8] Fickert M, Hoffmann J, Steinmetz M. Combining the Delete Relaxation with Critical-path Heuristics: a Direct Characterization[J]. Journal of Artificial Intelligence Research, 2016, 56(1): 269-327.

[9] Piotrowski W M, Fox M, Long D, et al. Heuristic Planning for PDDL+ Domains[C]//Workshops at the Thirtieth AAAI Conference on Artificial Intelligence. 2016.

[10] Krajňansky M, Hoffmann J, Buffet O, et al. Learning Pruning Rules for Heuristic Search Planning[C]//Proceedings of the Twenty-first European Conference on Artificial Intelligence. IOS Press, 2014: 483-488.

[11] Do M B, Kambhampati S. Sapa: A Multi-objective Metric Temporal Planner[J]. Journal of Artificial Intelligence Research, 2003, 20: 155-194.

[12] Muise C, Beck J C, McIlraith S A. Optimal Partial-order Plan Relaxation Via MaxSAT[J]. Journal of Artificial Intelligence Research, 2016, 57: 113-149.

[13] Marinescu L, Coles A. Heuristic Guidance for Forward-Chaining Planning with Numeric Uncertainty[C]//Proceedings of the Twenty-Sixth International Conference on Automated Planning and Scheduling (ICAPS 2016). AAAI Press, 2016: 230-234.

[14] Long D, Fox M. The 3rd International Planning Competition: Results and Analysis[J]. Journal of Artificial Intelligence Research (JAIR), 2003, 20: 1-59.

[15] Marzal E, Sebastia L, Onaindia E. Temporal Landmark Graphs for Solving Overconstrained Planning Problems[J]. Knowledge-Based Systems, 2016, 106: 14-25.

SearchPruningStrategyforMissionPlanninginLunarTeleoperation

Gao Wei1,2， Cai Dunbo3

1. School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100083, China 2. Beijing Aerospace Control Center, Beijing 100094, China 3. Hubei Provincial Key Laboratory of Intelligent Robot, Wuhan Institute of Technology, Wuhan 430205, China

Thewell-knownpruningstrategy“helpfulactions” (HA)isstudiedandextendedtothesettingsoftemporalplanningforChina’sLunarrover,whereresourcesarekeystosuccessfullyplan.Amorecapablepruningstrategycalled“resourceanalysisenhancedhelpfulactions” (RAEHA)isproposed.ThesetofRAEHAiscomputedthroughananalysisprocedureontherelationsamongresourcesandactions’effects.DuetoitsabilityinconsideringactionsthatareignoredbyHA,aplanningalgorithmisenabledbyRAEHAtosolveawiderrangeofproblemsthanHAdoes.TheexperimentalresultsshowthattheeffectivenessofRAEHAonasetofbenchmarksfortemporalplanningproblems.

Lunarteleoperation;Missionplanning;Pruningstrategy