基于微分平坦的升力式再入飞行器鲁棒姿态控制一体化设计

储 培 倪 昆 程 林 张庆振 程 阳

北京航空航天大学，北京100191

基于微分平坦的升力式再入飞行器鲁棒姿态控制一体化设计

储 培 倪 昆 程 林 张庆振 程 阳

北京航空航天大学，北京100191

针对升力式再入飞行器飞行过程中非线性、强耦合、快时变特性和外界干扰给姿态控制系统带来的挑战，提出了一种基于微分平坦的鲁棒姿态控制一体化设计方法。首先建立了升力式再入飞行器的姿态运动非线性数学模型，证明了该模型具有微分平坦性质。基于系统的平坦特性，通过微分同胚变换将模型转化为积分串联形式。在此基础上整体设计姿态控制器，实现姿态控制的一体化设计，相对于传统的时标分离方法，能更大限度地利用系统的性能，达到更好的控制效果，同时简化控制器设计过程，提高控制器设计效率。将非线性、强耦合、快时变造成的系统不确定项和外界干扰视为总扰动，设计了基于扩张状态观测器的补偿器，对总扰动进行动态观测并在控制器中实时补偿。仿真结果表明，提出的方法具有良好的姿态跟踪性能和较强的鲁棒性。

升力式再入飞行器;姿态控制；微分平坦；一体化设计；扩张状态观测器

近年来围绕高超声速飞行器控制的研究层出不穷，重点研究2类问题：吸气式高超声速飞行器的巡航控制问题和无动力高超声速飞行器的再入控制问题[1]，其中无动力高超声速飞行器飞行包线大，飞行环境恶劣，再入过程中具有强不确定性，飞行器本身具有非线性、强耦合和快时变的特点，这些因素给升力式再入飞行器的姿态控制带来了巨大挑战[2]。国内外文献主要采用滑模控制、动态逆控制和反演控制的设计方法设计高超声速飞行器的姿态控制系统[3-5]，但是这些文献普遍利用多时间尺度技术将模型划分为多回路结构，分别针对各回路设计控制器。但实际上，各回路之间并不独立，传统的多回路设计方法只能利用各自回路的信息，没有考虑相互之间的耦合关系，导致各回路之间缺乏协调匹配，无法充分发挥系统的最大潜力[6-7]。如果可以将各回路作为一个整体考虑，一体化设计控制器，则可以有效避免上述问题，解决各回路之间的矛盾，获得更好的控制效果[8]。

微分平坦(平坦)理论是由Michael Fliess于20世纪90年代针对非线性系统提出的一个概念[9]，之后由Martin,Murray以及Van Nieuwstadt等人进一步深入研究。微分平坦(平坦)揭示了系统的平坦输出的存在性，也就是非线性系统动力学特性的一种结构形式的存在性。该理论在分析系统结构以及进行二自由度控制器设计中作用显著，尤其对系统的整体分析和一体化设计具有独特的优势。平坦系统的一个基本性质就是可以通过微分同胚变化将整个系统转化为等效的线性形式[10]，如果可以证明系统是平坦系统，则可以从整体上对系统进行分析设计，从而简化控制器的设计过程[11]。目前，微分平坦已经应用于球棒系统[12]和倒立摆等控制之中[13]。

本文将微分平坦性质与飞行器的控制结合起来，提出一种基于微分平坦的飞行器鲁棒姿态控制一体化设计方法。首先证明了升力式再入飞行器姿态运动模型的平坦性，基于系统的平坦特性将模型转换为积分串联形式，然后设计了基于极点配置的误差反馈控制律，引入扩张状态观测器对总扰动进行补偿，最后进行了标称状态和参数拉偏状态下的仿真，仿真结果验证了本文提出方法的有效性和优越性。

1 升力式再入飞行器姿态控制模型

本文研究的对象是面对称构型升力式再入飞行器，为了简化建模，采用平面地球假设，飞行器视为质量不变、质心位置固定的刚体，基于上述假设，在苏式坐标系中建立升力式再入飞行器姿态控制非线性模型。

(1)

式中，α，β和μ分别表示攻角、侧滑角和倾侧角;ωx，ωy和ωz分别表示滚转、偏航和俯仰角速度；Jx，Jy和Jz分别表示绕机体坐标系x，y和z轴的转动惯量；Jxy表示惯量积；γ，χ分别表示弹道倾角、弹道偏角；l，m和n分别表示滚转、俯仰和偏航力矩，表达式如下：

(2)

式中，Q表示动压，S和L分别表示特征面积、特征长度，Cl，Cm和Cn分别表示滚转、俯仰和偏航力矩系数，可以根据气动数据插值得到。

2 模型平坦特性验证

2.1 平坦系统定义

平坦系统的所有状态量和输入都可以表示成平坦输出及其若干阶导数的关系式[13]。一个系统如果具有平坦性，则该系统就称为(微分)平坦系统，该系统的输出称为平坦输出[14]。

平坦系统的具体定义如下：

(3)

使得

(4)

2.2 模型平坦性证明

选择姿态变量作为平坦输出：

(5)

则

(6)

由式(1)前3个公式，可得如下关系式：

(7)

(8)

从式(1)后3个公式推出：

(9)

上式可以写成：

(10)

由式(8)和(10)可得：

(11)

综合式(6)、(8)和(11)，系统的所有状态和输入均可以表示成平坦输出y1，y2和y3及其一、二阶导数的表达式为

(12)

因此，原系统是平坦系统。

3 基于微分平坦的姿态控制一体化设计

传统的飞行器姿态控制器设计方法是根据时标

分离理论，将飞行器姿态运动分为慢变化的姿态角回路和快变化的角速度回路，独立设计2个回路的控制律。该方法利用的信息有限，各回路存在协调问题，设计的控制律具有一定的保守性，且各回路设计方法类似，设计过程冗余。

利用微分平坦特性的一体化设计不再区分单个回路，而是充分考虑各回路之间的耦合关系，将各回路作为一个整体考虑。因而可以更充分地发挥系统的潜能，不仅能够提升控制效果，还能使设计过程更加简洁流畅。

对式(7)求导：

(13)

式中：

(14)

令

(15)

基于精确模型跟踪误差的状态反馈控制律如下：

(16)

式中，vx，vy和vz为新的控制输入，结合式(13)，可得积分串联形式的闭环系统：

(17)

至此，利用系统的平坦特性将复杂的非线性模型的姿态控制转化为上述简单二阶线性模型的跟踪控制，只需针对上述二阶线性模型设计控制器就可以实现对整个系统的姿态控制。假设期望攻角、侧滑角和倾侧角分别为αd，βd和μd，基于极点配置的误差反馈控制律设计如下：

(18)

s2+ki1s+ki2=0, (其中，i=1,2,3)

(19)

由上式，姿态角跟踪误差的动态方程可以表示成如下的微分方程。

(20)

上式可以保证姿态角跟踪渐进稳定。将式(16)和(18)带入式(19)，可得控制输入如下：

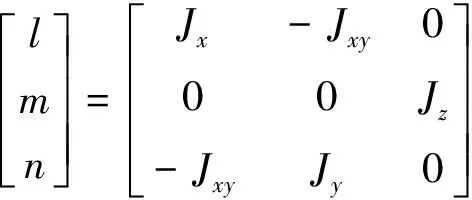
(21)

上述控制律的实现是基于精确模型假设，当系统存在模型不确定性和外界扰动时，单纯线性控制律并不足以保证系统的稳定性和鲁棒性。

4 基于ESO的补偿器设计

为了对系统不确定性进行补偿，引入扩张状态观测器(ESO)。ESO是自抗扰控制的核心，它能够对系统的总扰动进行动态观测并在控制器中进行补偿，且ESO的构建不依赖于精确模型，现已广泛应用于理论与实际控制系统中。

将式(16)改写成如下形式：

(22)

将式(1)后3个公式带入上式可得：

式中，

(23)

(24)

(25)

(26)

(27)

F和G均有名义值，但是不可能实时得到准确值，且外界扰动会使得系统不确定性进一步增强。因此，用参考值F*和G*代表F和G的确定部分，将不确定部分和外界扰动当作总扰动予以补偿。即：

(28)

式中，f表示外界扰动，a表示系统总扰动。因此，式(23)可以简化为：

(29)

需要说明的是，模型的信息和观测器的负担是互补的，模型信息了解得越充分，观测器的负担就越轻，反之则相反。虽然可以将式(23)中的F项全部视为扰动项，利用ESO观测出来，但是这样会使模型信息太匮乏，F项的表达式十分复杂且频率特性未知，这对观测器的设计提出很高的要求，而观测器设计的关键就是带宽，然而，观测器的带宽受到传感器噪声、采样频率和模型带宽的影响，不能任意取值，这样一来很可能导致观测效果不佳，影响最终的控制效果。故设计扩张状态观测器时，充分利用F项的已知信息，对于观测效果的提升有益。

为了便于构造扩张状态观测器，将上式写成如下形式：

(30)

构造如下的扩张状态观测器：

(31)

将式(30)与(31)作差，可得观测误差动态方程：

(32)

上式的特征多项式为：s3+β01s2+β02s+β03，根据文献[15]中用带宽参数化方法设计扩张状态观测器参数的方法，选择β01，β02和β03使特征多项式满足：

(s+ωo)3=s3+β01s2+β02s+β03

(33)

(34)

因此，最终需要补偿的控制量为：

ucomp=(G*)-1z3

(35)

最终的控制输入为：

u=u*-ucomp

(36)

式中，u*为式(21)得到的控制量。

理想力矩的实现是靠操纵舵产生的，因此，需要把力矩分配到3个舵面上。考虑舵偏与力矩的关系为：

(37)

解算出舵偏指令如下：

(38)

5 仿真结果分析

为了验证闭环系统的性能，在MATLAB/Simulink中进行仿真验证，仿真初始条件如表1所示。

表1 仿真初始条件

期望攻角、侧滑角和倾侧角分别为7°，0°和10°。各项参数设置为：k11=10，k12=5，k21=10，k22=5，k31=5，k32=10，ωo=10。

图1～3分别给出了没有模型误差和外界干扰情况下攻角、侧滑角和倾侧角的变化曲线。图1和3表明攻角和倾侧角都能很快跟上指令(2s左右)，基本无超调，无稳态误差。图2中侧滑角始终保持在0°附近(10-3级别)。这说明所设计的控制器在没有干扰和不确定条件下能够保证良好的跟踪性能。

图1 攻角跟踪曲线

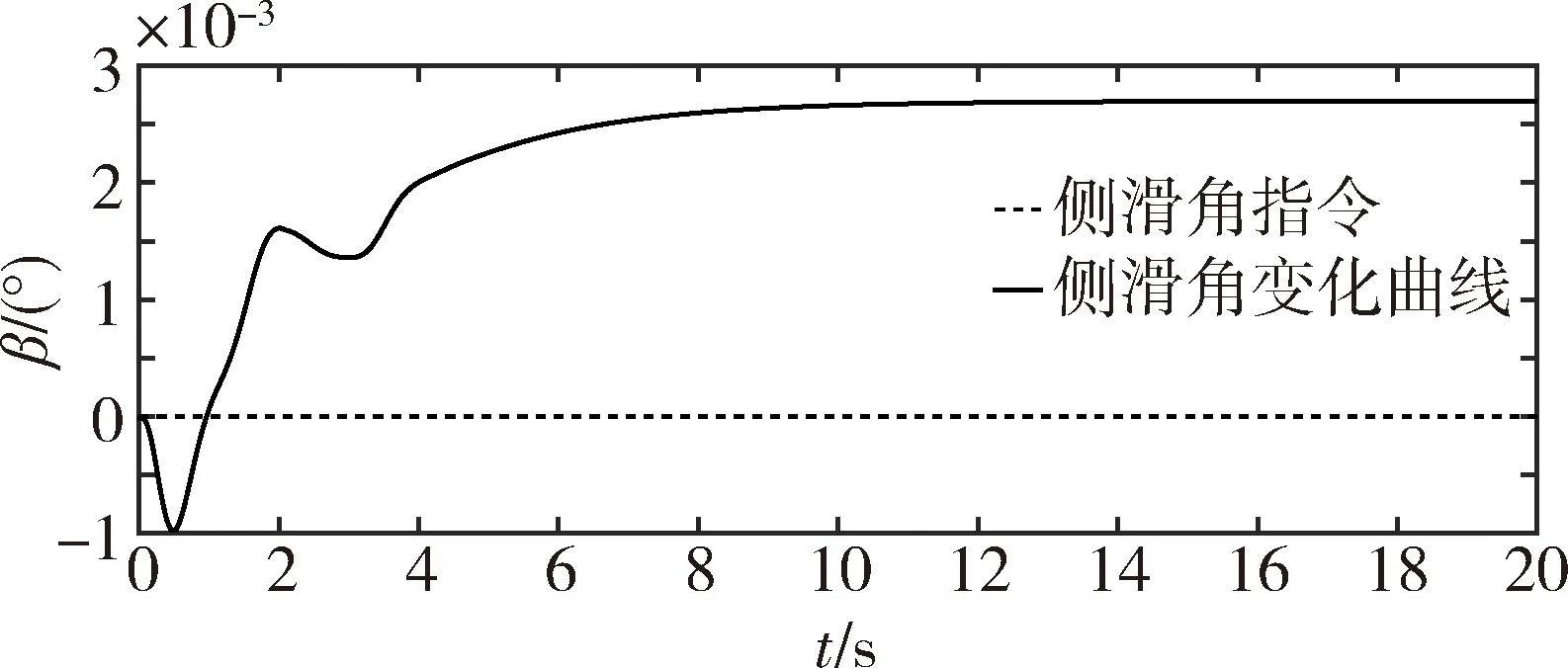
图2 侧滑角变化曲线

图3 倾侧角跟踪曲线

为了验证本文提出的一体化设计方法的优越性，将其与根据传统时标分离原理对内外环分别设计控制器的方法进行对比，控制律同样采用基于极点配置的误差反馈控制律，结果如图4～6所示。

图4 攻角跟踪效果对比图

图5 侧滑角变化对比图

图6 倾侧角跟踪对比图

为了更加直观地比较2种控制方法的控制效果，表2～4给出了各项指标的对比结果。

表2 攻角跟踪效果对比

表3 侧滑角变化对比

表4 倾侧角跟踪效果对比

表2～4表明本文提出的基于微分平坦的一体化设计方法在调节时间、超调量和跟踪误差上都普遍优于传统的时标分离法，控制效果更好。因为一体化设计方法能够从整体上对系统进行分析设计，而不必考虑各回路之间的约束关系，因此能更充分地发挥系统的潜能，达到更优的控制效果。一体化设计方法的优越性不仅体现在具体控制指标上，还表现在控制器设计过程的简洁高效上。传统时标分离法各回路都要独立设计控制器，最后还要组合在一起共同调试，一体化方法则从整体上一次性完成控制系统设计，效率更高。

为进一步验证控制系统的鲁棒性能，进行了参数拉偏条件下的仿真验证。拉偏条件如表5所示。

表5 参数拉偏条件

图7和8分别给出了参数拉偏情况下ESO估计姿态角和总扰动效果。由图7可知，ESO能快速、准确地跟踪攻角和倾侧角，侧滑角估计值虽然开始稍有偏差，但是始终在很小的范围内，最终能收敛到准确值。图8表明，ESO对系统的总扰动也有良好的跟踪效果，这也保证了参数拉偏情况下控制系统的跟踪性能和鲁棒性能。因此，所设计的ESO具有良好的估计效果。

图9给出了参数正拉偏、负拉偏和不拉偏情况下攻角、侧滑角和倾侧角变化曲线。由图可知，无论参数正负拉偏，控制系统均能保证快速、无稳态误差且微小超调地跟上攻角、倾侧角指令信号，侧滑角在参数拉偏条件下仍然能够保持在0°附近(10-3级别)。

图10给出了参数正拉偏、负拉偏和不拉偏情况下的舵偏曲线。除了升降舵会在开始阶段有较大幅度偏转，整个跟踪过程3个操纵舵都保持在合理的偏转范围内(-10°～10°)。

图7 ESO姿态角估计效果

图8 ESO总扰动估计效果

图9 参数拉偏情况下姿态角跟踪曲线

图10 参数拉偏情况下升降舵、副翼和方向舵变化曲线

6 结论

针对传统升力式再入飞行器姿态控制器设计中存在的问题，开展了基于微分平坦的一体化鲁棒姿态控制设计方法研究，主要有：

1)分析并验证了升力式再入飞行器姿态运动模型的微分平坦特性；

2)提出了基于微分平坦的姿态控制一体化设计方法；

3)将ESO与一体化设计相结合，设计了基于ESO的鲁棒姿态控制系统。

仿真结果表明：本文提出的方法相对于传统的时标分离方法具有更好的控制性能和良好的鲁棒性能，且设计过程更加简洁高效。

[1] 吴宏鑫, 孟斌，等. 高超声速飞行器控制研究综述[J]. 力学进展, 2009, 39(6):756-765. (Wu Hongxin, Meng Bin， et al. Overview of Hypersonic Vehicle Control Research [J]. Advances in Mechanics, 2009, 39(6):756-765.)

[2] 黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J]. 控制理论与应用, 2011, 28(10):1496-1505. (Huang Lin, Duan Zhisheng, Yang Jianying. Challenge of Control Science in Near Space Hypersonic Aircrafts [J]. Control Theory and Applications, 2011, 28(10):1496-1505.)

[3] 韩钊, 宗群, 田柏苓,吉月辉. 基于Terminal滑模的高超声速飞行器姿态控制[J]. 控制与决策, 2013, 28(2):259-263. (Han Zhao, Zong Qun, Tian Bailing, Ji Yuehui. Hypersonic Vehicle Attitude Control Using Terminal Sliding Mode Control [J]. Control and Decision, 2013, 28(2):259-263.)[4] 赵刚, 邵玮, 陈凯,等. 高超声速飞行器神经网络动态逆姿态控制器设计[J]. 系统仿真技术, 2010, 6(4):308-312. (Zhao gang, Shao Wei, Chen Kai, et al. Neural Network Dynamic Inversion Design for Hypersonic Attitude Control [J]. System Simulation Technology, 2010, 6(4):308-312.)

[5] 刘艳雯, 胡超芳. 基于反步法的高超声速飞行器终端滑模控制[J]. 火力与指挥控制, 2016, 41(9):28-31. (Liu Yanwen, Hu Chaofang. Terminal Sliding Mode Control for Hypersonic Vehicles Based on Backstepping [J]. Fire Control and Command Control, 2016, 41(9):28-31.)

[6] 薛文超, 黄朝东, 黄一. 飞行制导控制一体化设计方法综述[J]. 控制理论与应用, 2013, 30(12):1511-1520. (Xue Wenchao, Huang Chaodong, Huang Yi. Design Methods for the Intrgrated Guidance and Control System [J]. Control Theory and Applications, 2013, 30(12):1511-1520.)

[7] 舒燕军, 唐硕. 轨控式复合控制导弹制导与控制一体化反步设计[J]. 宇航学报, 2013, 34(1):79-85. (Shu Yanjun, Tang Shuo. Intrgrated Guidance and Control Backstepping Design for Blended Control Missile Based on NDO [J]. Journal of Astronautics, 2013, 34(1):79-85.)

[8] 董朝阳, 程昊宇, 王青. 基于自抗扰的反步滑模制导控制一体化设计[J]. 系统工程与电子技术, 2015, 37(7):1604-1610. (Dong Chaoyang, Cheng Haoyu, Wang Qing. Backstepping Sliding Mode Control for Integrated Guidance and Control Design Based on Active Disturbance Rejuction [J]. System Engineering and Electronics, 2015, 37(7):1604-1610.)

[9] Michel Fliess, Jean Levine, Philippe Martin, et al. Flatness and Defect of Non-linear Systems: Introductory Theory and Examples[J]. International Journal of Control, 1995, 61(6):1327-1361.

[10] Rigatos G G. Nonlinear Control and Filtering Using Differential Flatness Approaches[J]. Studies in Systems Decision amp; Control, 2015, 25.

[11] Sira-Ramirez H. A Flatness Based Generalized PI Control Approach to Liquid Sloshing Regulation in a Moving Container[C]// Proceedings of the American Control Conference. 2002:2909-2914 vol.4.

[12] Ramirez-Neria M, Sira-Ramirez H, Garrido-Moctezuma R, et al. On the Linear Control of Underactuated Nonlinear Systems via Tangent Flatness and Active Disturbance Rejection Control: The Case of the Ball and Beam System[J]. Journal of Dynamic Systems Measurement amp; Control, 2016, 138(10):376-380.

[13] Aguilar-Ibáez C, Sira-Ramírez H, Suárez-Castaón M S. A Flatness-Based Controller for the Stabilization of the Inverted Pendulum[J]. Mathematical Problems in Engineering, 2011, 2011(3):34-35.

[14] Carlos Aguilar-Ibáez, Hebertt Sira-Ramírez, Miguel S. Suárez-Castaón, et al. The Trajectory Tracking Problem for an Unmanned Four-rotor System: Flatness-based Approach[J]. International Journal of Control, 2012, 85(1):1-9.

[15] 韩京清. 自抗扰控制技术:估计补偿不确定因素的控制技术[M]. 国防工业出版社, 2008.

[16] Gao Z. Scaling and Bandwidth-parameterization Based Controller Tuning[C]// American Control Conference, 2003. Proceedings of the. IEEE, 2003:4989-4996.

RobustAttitudeControlofLiftReentryVehicleBasedonDifferentialFlatnessIntegratedDesign

Chu Pei, Ni Kun, Cheng Lin, Zhang Qingzhen, Cheng Yang

Beijing University of Aeronautics and Astronautics, Beijing 100191, China

Aimingatsolvingtheproblemsbroughtbythenonlinear,strongcoupling,fasttime-varyingcharacteristicsofthemodelandexternaldisturbance,anintegrateddesignmethodispresentedfortherobustattitudecontrolofliftreentryvehiclebasedondifferentialflatness,.Themathematicalmodelofthevehicleisfirstlyestablishedandtheflatnesspropertyofthesystemisverifiedafterwards.Thesystemistransformedintothelinearcanonicalformthroughdiffeomorphismthatistakenfulladvantageofthedifferentialflatnessofthesystem.Flatness-basedcontrollerisdesignedtofulfilltheattitudetrackingtaskdirectlyavoidingthetroubleofdesigninginner-loopandouter-loopcontrollerseparately.Byconsideringthesystemuncertaintiesandexternaldisturbance,extendedstateobserver(ESO)isintroducedtoobservetheuncertaintiesandcompensatethecontrollerinrealtime.Numericalsimulationsarepresentedtoassesstheeffectivenessandrobustnessoftheproposedcontrolstrategy.

Liftreentryvehicle;Attitudecontrol;Differentialflatness;Integrateddesign;Extendedstateobserver

TP273

A

1006-3242(2017)04-0003-08

2017-02-22

储培(1993-)，男，安徽池州人，硕士，主要研究方向为导航、制导与控制；倪昆(1991-)，男，苏州人，博士，主要研究方向为导航、制导与控制；程林(1989-)，男，山东临沂人，博士，主要研究方向为导航、制导与控制；张庆振(1976-)，男，江苏沛县人，博士后，主要研究方向为导航、制导与控制；程阳(1993-)，男，合肥人，硕士，主要研究方向为导航、制导与控制。