一道平面几何最值问题研究

朱记松 王子保

(1.安徽省太湖县晋熙中学，安徽 安庆 246400；2.安徽省天长市实验中学，安徽 滁州 239300)

一道平面几何最值问题研究

朱记松1王子保2

(1.安徽省太湖县晋熙中学，安徽 安庆 246400；2.安徽省天长市实验中学，安徽 滁州 239300)

本文通过对一道初等几何极值问题解题过程的质疑，提出了与它相关的一般性问题，通过数学建模、计算软件求解，发现原结果正确纯属偶然.

最值问题；数学建模；直觉思维；一般性

一、问题

问题：如图1，在△ABC中，AB=AC=5，BC=6，D是边BC上一动点，且D不与B、C重合，∠ADM=∠ADN=60°，分别交两边AB,AC于M，N点.

试求：DM+DN的最小值.(来自：数理化解题研究群)

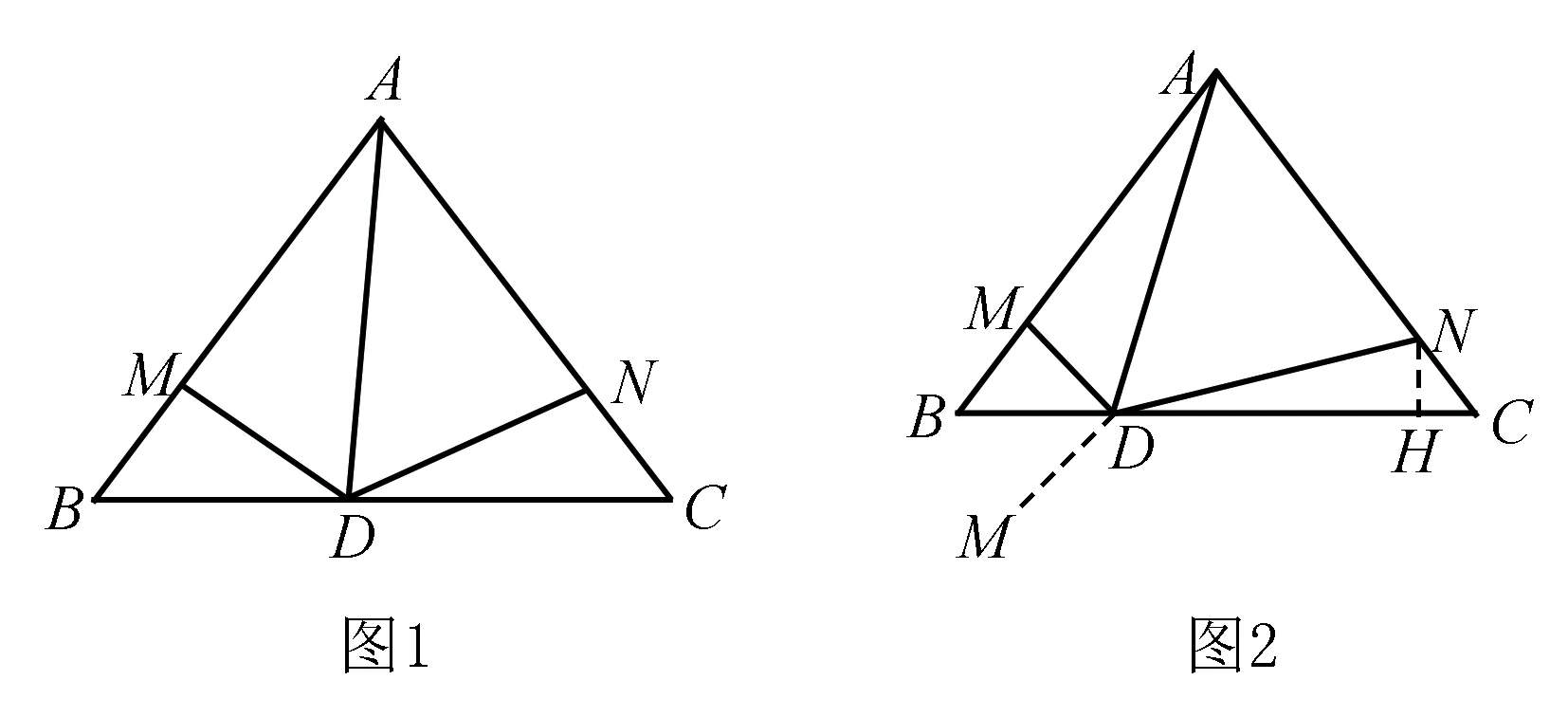
一位群友提供如下解法：

解作点M关于BC的对称点M′，连DM′，如图2示.

则DM=DM′,∠MDB=∠M′DB.故DM+DN=DM′+DN.

当且仅当D,M′,N′三点共线时DM+DN最小.

∵∠MDA=∠NDA=60°,∠MDB=∠M′DB,

∴∠MDB+∠CDN=∠M′DB+∠CDN=2∠CDN=60°,

∴∠BDM=∠NDC=30°.∴∠ADB=90°.即AD⊥BC时DM+DN最小.

经分析不难发现，上述问题解题思路是依靠数学直觉思维建立在“将军饮马”模型的基础上. 由于“将军饮马”使用人条件就模型的折线两端点的位置已经确定，而本题中的点M、N的位置均未确定，它们随着点D位置的改变而改变，因此笔者认为通过直觉思维获得解题思路不可靠.

二、一般性问题的提出

为不失一般性，我们提出如下问题：

如图3，在△ABC，AB=AC，AO⊥BC于点O，BC=2，AO=h,D是边BC上一动点，且D不与B、C重合，∠ADM=∠ADN=60°,分别交两边AB,AC于M，N点.试求DM+DN的最小值.(用h表示)

1.建立数学模型

不妨设OD=x,∠BAO=α,∠OAD=β.

∵AB=AC,∴∠BAO=∠CAO=α,BO=CO=1.

∴∠BMD=60°+α+β,∠DNC=60°+α-β,BD=1+x,CD=1-x.

记f(x)=DM+DN.

2.探索数学模型的解

由解析式f(x)=

探求f(x) 在不同h参数值下的最小值.由于这是一个非常规的初等函数，难以用初等方法求出其最值，因此笔者采用数学软件的方法探索模型的解.过程如下：

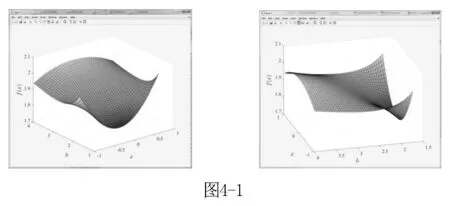
不难发现，随着h增大，f(0)由f(x)在取值范围x∈(-1,1)内的最小值渐变为最大值，而边界两点值从大变为最小值.

由函数曲面图可知，关键h值满足：f(±1)=f(0) .

当h≤hc时，f(0)是f(x)在取值范围x∈(-1,1)内的最小值.

但是注意，当h=hc时，f(±1)=f(0)是最小值，还有两个最大值未求出，如图4-2：

所以当h≥hc时，f(0)不会立即变为最大值，由于最大值不是我们考虑到主要问题，暂不叙述.

(3)数学模型的解

3.回到原问题

通过上述研究发现群友的思路是错误的，尽管他得到的结果正确，但纯属偶然.

[1]李汉龙，隋英，缪淑贤，韩婷.Mathematica基础培训教程[M].北京：国防工业出版社，2016:162.

[责任编辑：李克柏]

G632

A

1008-0333(2017)26-0023-02

2017-07-01

朱记松(1969.10-)，男，安徽安庆人，高级教师，本科学历，从事数学教学与解题研究.