Spark-GraphX框架下的大规模加权图最短路径查询

宋宝燕，张永普，单晓欢

(辽宁大学 信息学院，辽宁 沈阳 110036)

Spark-GraphX框架下的大规模加权图最短路径查询

宋宝燕，张永普，单晓欢*

(辽宁大学 信息学院，辽宁 沈阳 110036)

最短路径问题一直是计算机等学科的热点研究问题，常应用于社交网、交通网等诸多领域.图规模爆炸式的增长导致传统单机环境下的存储、查询已无法满足大规模图的处理需求.提出一种基于Spark-GraphX平台的大规模图最短路径查询方法(LSGSP-SG)：首先利用经典算法对大规模图进行分割并标记，将割点的信息记录在文本文件中，然后利用大数据平台Spark的GraphX框架进行迭代式分布计算并进行各个计算机节点的消息通信及同步，最后返回最短路径查询结果.

Spark；图分割；最短路径；分布式

0 引言

图可以反应现实世界实体间的复杂关系，图中节点表示实体对象，实体间的联系则通过边表示[1].现实应用中的设备更新问题、工程问题、路线推荐等均可转换为最短路径查询问题求解.图规模较小时，判断过程简单，因此经典最短路径查询方法均采用单机存储计算模式，然而随着信息技术的发展，实体间联系越来越复杂，导致图规模迅速膨胀，经典方法已无法适应大规模图[1]的处理需求，分布式并行技术因可良好地满足大数据处理而被广泛应用，因此研究适合大规模图数据的并行计算算法成为新的研究热点.

Spark是一种与 Hadoop 相似的分布式并行计算平台，两者之间的不同在于其启用了内存分布式数据集，除了能够提供交互式查询外，还可以优化迭代工作负载.GraphX是Spark的子框架，是Spark处理图的有力工具，采用GAS模型，利用Spark提供的内存缓存RDD，实现高效的图计算.本文提出一种基于Spark-GraphX的最短路径算法，首先利用已有分割算法将大规模图进行分割存储，然后将割点的信息记录在文本文件中，最后利用大数据平台Spark的GraphX框架进行迭代式分布计算并进行各个计算机节点的消息通信及同步，最后返回最短路径查询结果.

1 相关工作

1.1 最短路径查询算法

最短路经典算法包括Dijkstra算法[2]、 Floyd算法[3]及Bellman-Ford算法[4]等.Dijkstra算法是求一个顶点到其余各顶点的最短路径，Floyd算法是一种利用动态规划的思想寻找加权图中多源点之间最短路径的算法，Bellman-ford算法是求含负权图的单源最短路径算法.上述算法应用于大规模图时，常因存储开销大、查询效率低等原因无法满足现有的查询需求.

1.2 图分割及Spark-GraphX

●图分割

由于图规模庞大，单节点无法存储完整数据图，因此考虑将图进行分割并分别存储于不同的计算机节点上.高效的图分割算法是提高大规模图计算的有效手段，大规模图有两种分割策略：一种是边分割策略，即将边打破，分别存储到两个计算机节点上，如图1所示；另外一种则是点分割策略，即将顶点复制存储到不同的计算节点上，如图2所示.两种策略各有优劣，目前点分割策略被广泛应用.Guerrieri等人提出了基于点分割的D-fep算法[5]，该算法大大减少了跨机器通信开销，进一步表明了点分割的优势.

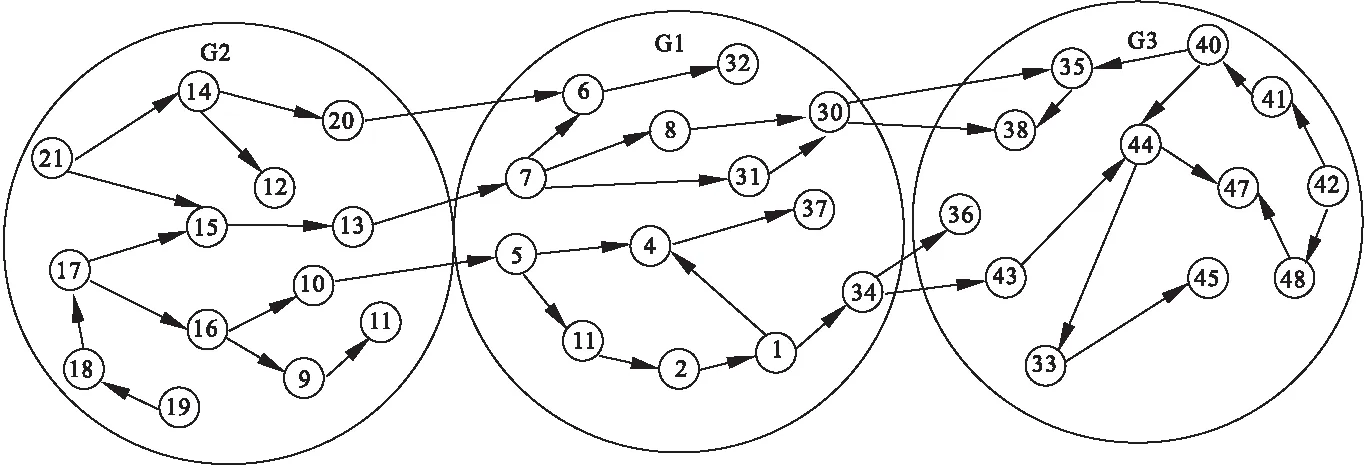
图1 边分割策略

图2 点分割策略

●Spark-GraphX

GraphX是Spark的子框架，是Spark处理图的有力工具.GraphX框架参考并优化了分布式图计算框架Pregel，采用GAS模型，利用Spark提供的内存缓存RDD，实现高效的图计算.

GraphX的核心抽象是Resilient Distributed Property Graph，一种点和边都带属性的有向多重图.它扩展了Spark RDD的抽象，有Table和Graph两种视图，只需要一份物理存储.两种视图都有自己独有的操作符，从而获得了灵活操作和执行效率[6].GraphX的代码结构整体如图3所示，其底层设计有以下几个关键点.

1)GraphX对图的所有操作最终都会转换成一系列的RDD操作来完成.

2)物理数据由RDD[Vertex-Partition]和RDD[EdgePartition]这两个RDD组成.点和边实际都是存储在带索引结构的分片数据块中，不变的索引结构在RDD转换过程中是共用的，降低了计算和存储开销.

3)图的分布式存储采用点分割模式，而且使用partitionBy方法，由用户指定不同的划分策略(PartitionStrategy).划分策略会将边分配到各个EdgePartition，顶点Master分配到各个VertexPartition，EdgePartition也会缓存本地边关联点的Ghost副本.

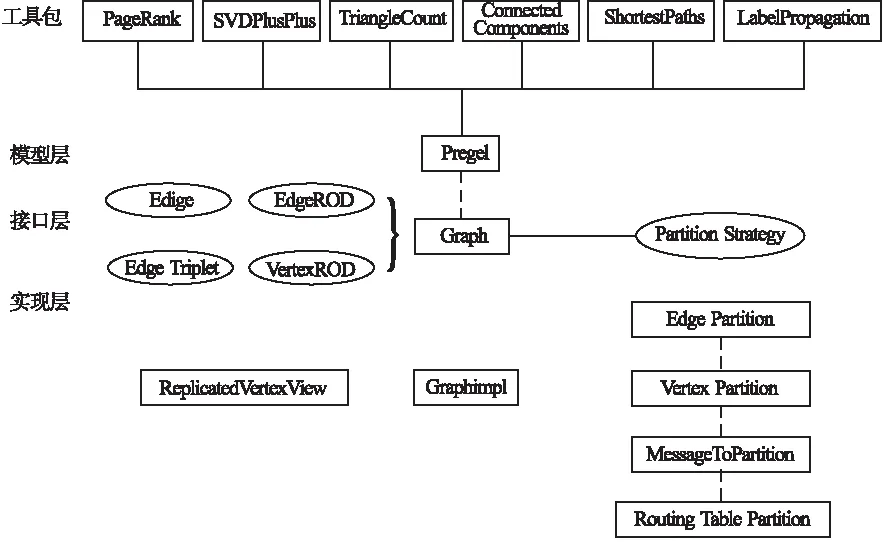
图3 GraphX的代码结构

但是Spark自带的最短路径算法不支持自定义权重，显然这是不符合现实生活的，比如在地图中，可以根据最短路径为用户推荐线路，此时则需要利用权重信息.因此本文对该算法进行优化，自定义加权DAG图来计算源点到目的点的最短路径.

2 大规模图最短路径查询方法

2.1 大规模图分割

本文首先利用D-fep算法进行图分割，该算法采用点分割策略，对某些与其他点联系较少的点进行分割，复制到不同的计算机节点进行存储，以保证负载均衡.同时，为满足后文的计算需求，本文将记录分割信息和存储节点序号.为避免混淆，本文将图中的点称之为顶点，将集群中其他计算机称之为节点.分割之前如图4所示.

图4 DAG图分割前

分割后的顶点和边分别存储在不同的计算机节点上，例如对于顶点20，master节点记录分割信息和存储信息{20，<1,2>}，表示该点为割点，分别存储在节点1和节点2上，如图5所示.对于顶点8，存储信息为{8，<1>}，表示该点为非分割点，储存在节点1上.

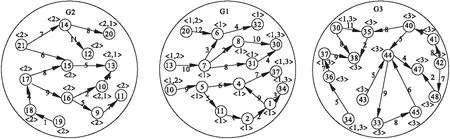
图5 分割后子图

2.2 基于Spark-Graphx的最短路径查询方法

本文提出的LSGSP-SG算法是将大规模图利用已有的分割算法进行分割，并利用本文给出的标记方法进行标记.当查询到达时，通过分析两点之间的信息判断是否在同一存储节点上，分别给出类集中式方法和分布式方法.在介绍算法之前，我们先来介绍几个概念：

顶点Vertex(Id,Property(V))，每个顶点由一个64位数字标识，其中Id表示顶点编号，Property则表示该顶点的属性，本文中存放该点到源点的距离和顶点所在节点序号.

边Edge(SrcId,DstId,Property(E))，其中SrcId代表源顶点Id，DstId代表目的顶点Id，Property代表边的权值.

三元组Triplet({SrcId,Property(V)},{DstId,Property(V)},{Property(E)})详细记录源点和目的点以及二者的权值.

●类集中式方法

若查询为1->4的最短路径，首先通过查询文件信息，根据点所在节点序号第一位是否相同判断两点是否属于同一节点，若是，则采用类集中式方法查询，具体步骤如下：

1) 首先设置源点属性值为0，其他点的属性为无穷大并初始化一个空队列；

2) 对源点的邻接点进行遍历，若该点不在队列中，则判断源点的属性值与到该点的边权值之和是否小于该邻接点的属性值，若是且无下一个邻接点，则修改该点的属性值为源点的属性值与到该点的边权值之和，否则继续判断下一个邻接点，将属性值小的点入队列，并记录该路径；

3) 将该点作为新的源点，迭代循环(2)；

4) 将每个点的Id作为key，该点到源点的距离作为value进行结果合并，得到该点到初始源点的最短路径.

●分布式方法

master节点接收查询需求后，通过判断顶点存储文件信息，若顶点x和顶点y所在序号第一位不相同，则采用分布式方法查询，该方法最短路径查询具体步骤如下：

1) master节点查询文件中割点集合P(x)、P(y)；

2) 将顶点x到割点集合P(x)的查询发送到对应的节点，同时将割点集合P(y)到顶点y的查询发送到对应的节点；

3) 各个节点分别计算顶点x、顶点y到P(x)和P(y)上割点之间的最短路径，得到相应的最短路径集合；

4) master节点将两个最短路径集合进行合并，得出顶点x到顶点y的最短路径集合；

5) master节点将最短路径集合返回客户端，算法结束；

以类集中式查询为例，若客户端需要查询顶点v19→v13的最短路径，master通过读取顶点存储文件信息，判断出顶点v19和顶点v13同属于节点2，此时采用类集中式方法，即：将该查询发送到节点2，由节点2进行查询，查询完毕后将结果返回master，master接收结果后返回给客户端，至此，一次路径查询结束.

节点2查询过程如下：

1)设置v19为源点，其属性值为0，其他顶点属性值为无穷大，初始化一个空队列；

2)判断邻接点v18是否在队列中，若不在，判断v19的属性值和邻接点v18之间边的属性值之和是否小于无穷大，若是，继续判断v19是否存在下一个邻接点，若存在，则继续判断v19到该邻接点的属性值之和是否小于上一个邻接点属性值之和，若小于，则设置该点到v19的属性值并将该点入队列，否则，将v18入队列；

3)将v18设置为源点，循环迭代2)，直到终点v13；

4)将顶点v19，v18，v17，v15，v13的id作为key，属性值作为value进行合并，得到最短路径为18；

5)节点2将该结果返回master，master返回给客户端，查询结束.

3 实验分析

3.1 实验环境及数据集

本文所有实验均在由三台计算机建立的Spark集群上完成，一台作为集群的主机master，另外两台作为集群的分机slave.每台计算机配置为英特尔双核CPU 3.00 GHz，6G内存，1T硬盘，均装有Ubuntu 14.04 LTS操作系统，使用Spark 2.1.1开发环境，开发语言为Scala.本文采用Scale-Free模型生成图模型，生成的图数据如表1所示.

表1 数据集参数

3.2 实验结果分析

本文在不同规模数据集上进行实验，以验证LSGSP-SG算法与Dijkstra算法、D-CH算法[6]的优劣如图6所示.根据实验结果可以看出，当图规模较小时，D-CH 算法查询时间最长， Dijkstra 算法次之，LSGSP-SG算法的查询时间最短.随着图规模的增大，传统算法时间复杂度明显增加，hadoop平台下查询时间次之，而LSGSP-SG算法查询时间依然最短，且随着图规模的增大，差距越来越明显.

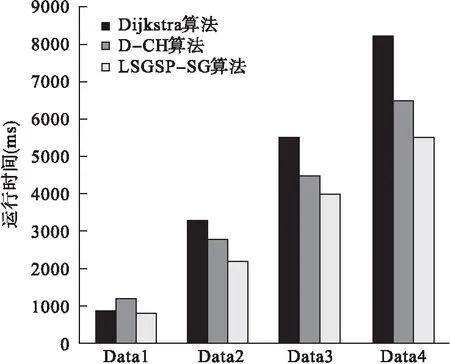
图6 算法运行时间对比图

4 结束语

随着图规模的增大，单机环境已无法满足数据图的存储及最短路径查询需求.本文提出的基于Spark-GraphX的大规模图最短路径查询方法采用分布式的处理技术，可有效解决任何规模图数据的最短路径查询问题.

[1] 富丽贞，孟小峰.大规模图数据可达性索引技术：现状与展望[J].计算机研究与发展，2015，52(3):116-129.

[2] Dijkstra E.W.A note on two problems in connexion with graphs[J].Numerische Mathematik,1959,1(1):269-271.

[3] Ford L,Fulkerson D.Flows in Networks[M].Princeton NJ:Princeton University Press,1962.

[4] 谢希仁,陈鸣,张兴元.计算机网络[M].北京：电子工业出版社，1994.

[5] Guerrieri A,Montresor A.Distributed Edge Partitioning for Graph Processing[J].Eprint Arxiv,2014,32(1):48-74.

[6] 黄明，吴炜.快刀初试：Spark GraphX在淘宝的实践[EB/OL].http://www.csdn.net/article/2014-08-07/2821097?locationNum=3,2017-08-01.

[7] 宋宝燕，张瑞浩，单晓欢.一种基于Hadoop的大规模图最短路径查询方法[J].辽宁大学学报：自然科学版,2016,44(2):109-113.

(责任编辑郑绥乾)

AShortestPathMethodonLarge-scaleGraphBasedonSpark-GraphX

SONG Bao-yan,ZHANG Yong-pu,SHAN Xiao-huan*

(InformationCollege,LiaoningUniversity,Shenyang110036,China)

The shortest path problem has always been a hot topic in computer science and other issues,often used in social networks,transportation networks and many other areas.The increase of graphs leads to the storage of the traditional stand-alone environment,and the query can not meet the processing requirements of large-scale graphs.In this paper,we propose a LSGSP-SG method based on the Spark-GraphX platform.Firstly,we use the classical algorithm to segment and mark the large-scale graphs,and record the information of the cut in the text file ,Then use the large data platform Spark′s GraphX framework for iterative distribution calculation and the various computer nodes in the message communication and synchronization,and finally the shortest path calculation results output to the client.

Spark，graph partition，shortest path，distributed

TP 311

A

1000-5846(2017)04-0289-05

2017-08-15

国家自然科学基金项目(61472169，61502215)资助

宋宝燕(1965-)，女，满族，辽宁开原人，教授，主要研究方向：大数据技术、数据库技术，图数据技术等，E-mail：bysong@lnu.edu.cn;

张永普(1994-)，男，汉族，山东菏泽人，硕士研究生，主要研究方向：图数据技术.

*

单晓欢(1987-)，女，汉族，辽宁沈阳人，助理实验师，主要研究方向：大数据技术，图数据技术.