拟möbius梯子的(1,1)-全标号

蔡汉桥，陈 洁，吕大梅

(南通大学 理学院，江苏 南通 226007)

拟möbius梯子的(1,1)-全标号

蔡汉桥，陈 洁，吕大梅*

(南通大学 理学院，江苏 南通 226007)

图的(1,1)-全标号是从点集及边集到非负整数集的一个函数f，且满足：任两相邻顶点标号相异；任两相邻边标号相异；及任关联的点和边标号也相异.本文对拟möbius梯子的(1,1)-全标号进行研究,确定了拟möbius梯子的(1,1)-全标号数.

L(1,1)-标号;L(1,1)-标号数;拟möbius梯子

0 引言

图的距离2标号问题是无线电通信波段分配问题的图论模式。Griggs和Robert[1]在此问题的基础上，提出图的L(2,1)-标号概念,并推广为L(h,k)-标号问题。之前，Robort[2]把h=1,k=1情形即L(1,1)-标号，作为组合分配问题进行研究。关于L(1,1)-标号的研究,参见综述[4-6].

一个简单图G的L(1,1)-标号指的是从顶点集V(G)到非负整数集的一函数f，且当d(u,v)=1时,有|f(u)-f(v)|≥1；当d(u,v)=2时，有|f(u)-f(v)|≥1。不妨设最小标号为0。则图G的所有L(1,1)-标号下的跨度max{f(v);v∈V(G)}的最小值称为G的L(1,1)-标号数，记为λ(G)。

1995年，Whittlesty[3]等人研究了一个很有趣的问题——剖分图的L(2,1)-标号。2002年，Havet和Yu[7-8]把G的剖分图的L(2,1)-标号称为G的(2,1)-全标号，并推广研究了(d,1)-全标号概念。接下来我们先给出(1,1)-全标号的定义。

一个图G的(1,1)-全标号指的是从点集及边集到非负整数集的一个函数f，且：任两相邻顶点标号相异；任两相邻边标号相异；以及任关联的点和边标号也相异。不妨设最小标号为0。则G所有(1,1)-全标号下的跨度max{f(v);v∈V(G)∪E(G)}的最小值为图G的(1,1)-全标号数，记为λT(G)。

文献[9-12]对拟梯子和拟Möbius梯子的L(1,1)和L(2,1)-标号进行了研究.本文将研究拟Möbius梯子的(1,1)-全标号。下面我们给出拟Möbius梯子的定义。

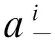
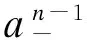
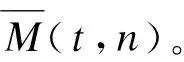
由于拟Möbius梯子的(1,1)-全标号即其剖分图的L(1,1)-标号。因此本文第1节中，我们先研究拟Möbius梯子的剖分图的L(1,1)-标号；而第2节则是在第1节结果基础上，给出拟Möbius梯子的(1,1)-全标号数。

引理1.1[5]设G是最大度为Δ≥2的图，λ(G)≥Δ。

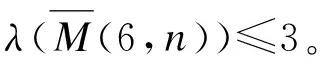
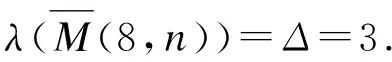
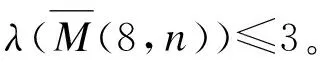
图1

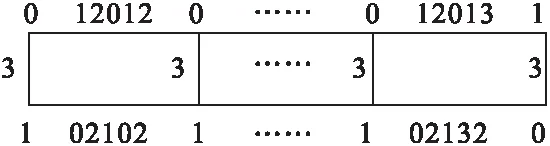
图2

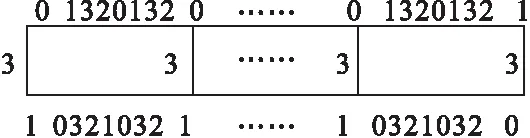
图3

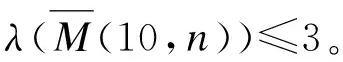
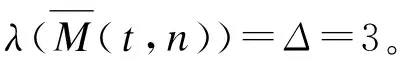
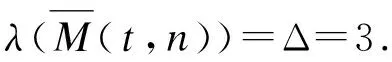
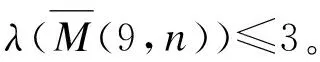
图4

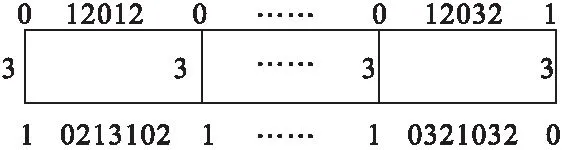
图5

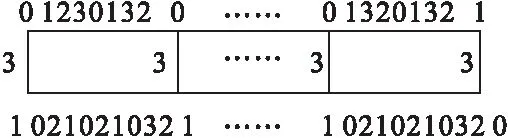
图6

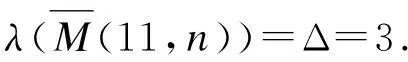
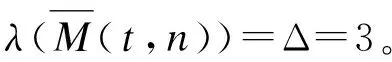
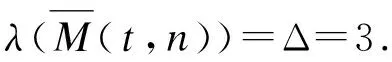
2 M(t,n)的(1,1)-全标号

由于拟Möbius梯子的(1,1)-全标号即其剖分图的L(1,1)-标号。从而由第1节，拟Möbius梯子的(1,1)-全标号数的结论如下。

定理2.1当t≥6时，λT(M(t,n))=Δ=3。

[1] Griggs J R，Yeh R K.Labeling graphs with a condition at distance 2[J].SIAM J.Disc.Math,1992,5:586-595.

[2] Borodin O V,Kostochka A V，Woodall D R.Total colorings of planar graphs with large maximum degree[J].J.Graph Theory,1996,26:53-59.

[3] Whittlesey M A,Georges J P,Mauro D W.On the lambda-number of Q_{n} and related graphs[J].SIAM J.Discrete Math,1995,8:449-506.

[4] Calamoneri T.The L(h,k)-labelling problem:a survey and annotated bibliography[J].Comput J,2006,49(5):585-608.

[5] Yeh RK.A survey on labeling graphs with a condition at distance two[J].Discrete Math,2006,306:1217-1231.

[6] Griggs J R,Jin X T.Recent progress in mathematics and engineering on optimal graph labellings with distance coditions[J].J Comb Optim,2007,14(2-3):249-257.

[7] Havet F.(d,1)-total labeling of graphs[R].Workshop Graphs and Algorithms,Dijon(FRANCE),2003.

[8] Havet F,Yu M L.(d,1)-total labeling of graphs[R].Technical Report 4650,INRIA,2002.

[9] 杜娟,吕大梅,李冬冬,等.拟梯子的L(2,1)-标号[J].辽宁大学学报：自然科学版,2013,4:308-313.

[10] 丁海燕,吕大梅,王金华,等.拟Möbius梯子的L(2,1)-标号[J].辽宁大学学报：自然科学版,2014,4:293-299.

[11] 严冬梅,吕大梅.拟梯子的L(1,1)-标号[J].辽宁大学学报：自然科学版,2015,4:296-300.

[12] 吴飞， 吕大梅.点接拟梯子的L(1,1)-标号[J].辽宁大学学报：自然科学版,2016,1:1-6.

(责任编辑郑绥乾)

The(1,1)-total-labelingsoftheSimilarityMöbiusLadders

CAI Han-qiao,CHEN Jie,LV Da-mei

(Departmentofmathematics,NantongUniversity,Nantong226007,China)

An(1,1)-total-labeling of a graph is a function f from the vertex set and edge set to the set of all nonnegative integers such that the labels are different for two adjacent vertices,two adjacent edges,and for a vertex and an edge which are incident.In this paper,we study the (1,1)-total-labeling of the similarity möbius ladders,and determine the (1,1)-total-labeling number of the similarity möbius ladders.

L(1，1)-labeling;L(1，1)-labeling number;similarity möbius ladder

O 157.5

A

1000-5846(2017)04-0302-04

2017-08-02

国家自然科学基金(11371207),江苏省自然科学青年基金(BK20140424)，南通大学校级基金(14ZY009),南通大学大学生创新训练计划项目(2017059)

蔡汉桥(1986-),女,研究生,教师,从事运筹学与控制论研究.

吕大梅(1976-)，女，副教授，从事运筹学与控制论.