基于有限新息率(FRI)的激光测距脉冲串信号的采样与重构

吴新杰 ，闫诗雨，徐西伦

(辽宁大学 物理学院 ，辽宁 沈阳 110036)

基于有限新息率(FRI)的激光测距脉冲串信号的采样与重构

吴新杰 ，闫诗雨，徐西伦

(辽宁大学 物理学院 ，辽宁 沈阳 110036)

为了降低对脉冲串激光测距仪器的采样硬件的要求.应用有限新息率理论(FRI)，对模拟脉冲串信号以略高于其新息率的速率进行采样，并应用sinc采样核与谱分析方法对其进行重构.仿真实验表明，本方法能够以远低于脉冲串信号奈奎斯特采样频率对其进行有效采样和重构.这为保证采样精度的同时，降低激光测距脉冲串采样硬件要求提供一种新思路.

激光测距；脉冲串信号；有限新息率；sinc采样核；谱分析方法

0 引言

近年来，脉冲式激光测距方法因其所具有的响应速度快、测量距离远、无需合作目标的优点，得到了长足的发展.目前脉冲式激光测距方法，已经在国防、军工、空间探测等领域得到广泛应用[1-2].脉冲式激光测距方法可以按发送脉冲数分为单脉冲激光测距方法和脉冲串激光测距方法.其中脉冲串激光测距方法由于相干性更高，能够有效地对回波信号进行相关处理的优势，在远距离高精度激光测距方面有更广泛的应用[1].脉冲串激光测距方法，是对其发射脉冲串和回波脉冲串进行一系列计算得到测量距离的[3-4].因此对其回波脉冲串的准确采样和重构就变得十分重要.传统奈奎斯特采样理论，需要使采样频率大于其信号频率的二倍才可完成采样与重构，在实际应用中这无疑对于采样硬件提出了很高的要求.

有限新息率(Finite Rate of Innovation，FRI)理论于2002年由Vetterli等人提出，这为脉冲串信号的采样和恢复开启了新思路[5].本文应用有限新息率，以稍高于信号新息率的频率，较高精度的完成对于模拟回波脉冲串信号的采样与重构，这对于脉冲式激光测距设备的制作有很强的实用意义.

1 脉冲串信号的新息率

脉冲串信号可以表示为一系列已知的单脉冲(单脉冲数目为K)的组合.对于这样的脉冲串信号，可以以其自由参量(延迟时间和不同的幅值)完满表示.因此在一定的时间T内，其自由参量数目(2K)是有限的.我们称2K/T为该脉冲串信号的新息率.对于这样的信号我们可以称其是FRI(Finite Rate of Innovation)信号.

脉冲串式激光测距中的回波脉冲信号就是一种FRI信号，其由K个激光回波脉冲组成.其具有如下形式：

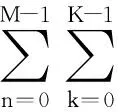
(1)

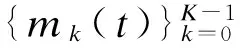
2 脉冲串信号的采样

对于FRI信号应选取合适的采样核函数对其进行处理.根据文献[6-7],含有2K个未知量的y(t)可以由2K个测量值恢复.也就是只要确定脉冲串信号在时间周期T内的幅值和相位即可得到该脉冲串信号.

例如如下周期为τ的脉冲串序列：

(2)

对上式用傅里叶级数展开有：

(3)

上式中傅里叶级数系数表示为：

本文以混凝土热传导原理为基础，用comsol软件对实际工程案列进行仿真模拟计算，用以分析如何对大体积混凝土温度裂缝进行控制，得出以下结论:

(4)

将式(2)式(4)联立得：

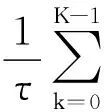
(5)

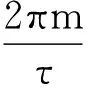
(6)

对于激光测距回波脉冲串信号，其基本脉冲信号波形为已知，获得回波脉冲串信号的连续傅里叶系数子集成为首要问题.结合现有经验，将待测信号进行低通滤波后，以所用低通滤波器的截至频率的2倍对其进行采样，进而利用离散傅里叶变换处理采样值是最直接获取信号连续傅里叶系数子集的方法.这里我们选用sinc采样核函数对激光测距脉冲串信号进行处理，sinc采样核实际上等同于一个理想状态的低通滤波器.

其表达式为：

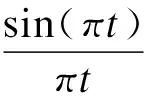
(7)

Sinc采用核函数时域波形为图1.

图1 sinc采样核函数时域波形图

本文，利用谱分析中湮灭滤波器重构方法，估计出经采样核函数处理后的激光测距回波脉冲串信号的时延和幅度参数.

3 信号的重构方法

(8)

(9)

其中qk满足：

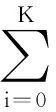
(10)

用矩阵形式表示式(10)，令q0=1，得到式：

(11)

由上式可知，要求取湮灭滤波器系数{qk}，需要至少获得2K+1个Y[m]的值.再得到{qk}的值后，对其进行Z变换，而后求其零点，其零点值即为Wk的值.再得到Wk的值之后，由Wk和tk的关系式，可得tk的值.

再重构出时延参数tk后，应用最小二乘法求解下式即可重构出幅值参数.

(12)

到此，重构出激光测距回波脉冲串信号的幅值与时延参数，也就完成了激光测距回波脉冲串信号的重构.

4 仿真结果

为验证本方法能否对激光测距回波脉冲串信号完成高精度采样与重构.本节利用matlab软件进行有限新息率对激光测距回波信号的采样重构仿真实验.本仿真选取信号为常见脉冲串信号，幅值参数为{1.5;2.3;3.2;2.5;3.3},时延参数为{0.1;0.3;0.5;0.7;0.9}，周期为1秒，单周期脉冲个数为5.特殊说明本仿真实验测试环境为纯净环境，未叠加噪声.

模拟激光测距回波脉冲串原始狄拉克流图为图2.

模拟激光测距回波脉冲串原始狄拉克流信号与其重构信号如图3.

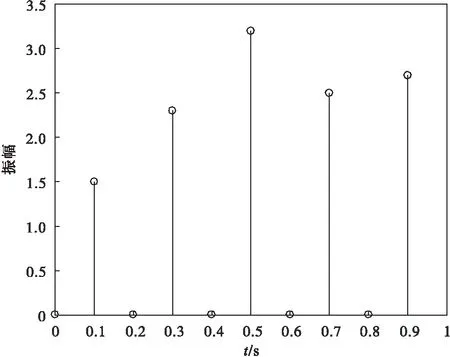
图2 模拟激光测距回波脉冲串原始狄拉克流图

图3 拟激光测距回波脉冲串原始狄拉克流信号与其重构信号图

对比图2和图3可知，应用sinc采样核和湮灭滤波器的有限新息率方法，能够对模拟激光测距回波脉冲串信号精准重建.为更加科学的衡量重建精准度，引入相对误差计算公式：

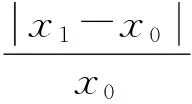
(13)

其中x1为重构值，x0为真实值.

时延参数重构相对误差水平如表1.

表1 时延参数重构相对误差

幅值参数重构相对误差水平如表2.

表2 幅值参数重构相对误差

由表1，表2中时延参数和幅值参数相对误差数据可知，在纯净环境下，应用sinc采样核和湮灭滤波器的有限新息率方法可以较高精确度地对激光测距回波脉冲串信号完成采样与重构.基于有限新息率的激光测距回波脉冲串信号的采样重构方法达到了较高水平.

5 结论

实际中常用的中远距离激光测距设备晶振频率一般为15 MHz或以上.根据仿真实验结果并结合实际应用情况，仅考虑脉冲串信号重构误差的情况下，可知以本文采样与重构方法误差导致的测距误差是μm级别，这样的误差对测量精度影响是微弱的，是可以接受的，因此应用本方法并不会降低脉冲式激光测距设备的精度.同时本方法的采样数目约为激光测距回波脉冲串信号新息参量数，对比奈奎斯特采样定律的采样数大大减少.本方法也为在保证激光测距仪器精度的前提下，降低仪器采样硬件要求提供一种新思路.

[1] 钟声远,李松山.脉冲串激光测距技术研究[J].激光与红外,2006,(S1):797-799.

[2] 胡凯.远程激光测距中的脉冲串互相关技术研究[D].杭州：浙江大学,2013.

[3] 黄震,徐国雄,倪旭翔,等.数字相关检测技术扩大脉冲式激光测距测量范围的研究[J].仪器仪表学报,2003,24(4):266-268.

[4] 周健,龙兴武.多点分层差动激光多普勒自身测速仪的研究[J].中国激光,2010,37(07):1837-1844.

[5] M Vetterli,P Marziliano,T Blu.Sampling signals with finite rate of innovation[J].IEEE Transactions on Signal Processing,2002(50):1417-1428.

[6] Mishali M,Eldar Y C,Dounaevsky O,et al.Xampling:Analog to digital at sub-Nyquist rates[J].IET Journal of Circuits,Devices and Systems,2011,5(1):8-20.

[7] Wagner N,Eldar Y C,Friedman Z.Compressed beamforming in ultrasound imaging[J].IEEE Transactions on Signal Processing,2012,60(9):4643-4657.

(责任编辑郑绥乾)

TheSamplingandReconstructionoftheLaserRangingPulseTrainsSignalsBasedonFiniteRateofInnovation(FRI)

WU Xin-jie，YAN Shi-yu，XU Xi-lun

(SchoolofPhysics,LiaoningUniversity,Shenyang110036，China)

In order to reduce the requirement of digital sampling hardware for pulsed laser ranging instrument,this paper presents a method by using the theory of finite rate of innovation ,which can sample the simulated pulse trains signals with a rate of slightly higher than their rate of innovation,and reconstruct them by using sinc sampling kernel and spectrum analysis method.The simulation results show that the method can effectively sample and reconstruct the pulse trains signals with a rate far below their Nyquist sampling frequency.This paper provides a new way to reduce the requirement of laser ranging with the high precision of sampling accuracy.

laser ranging;pulse trains signals;finite rate of innovation;sinc sampling kernel;spectrum analysis method

TQ 911.7

A

1000-5846(2017)04-0315-05

2017-09-01

吴新杰(1964-)，男，汉族，辽宁沈阳人，教授，博士，主要从事层析成像技术、智能优化算法、信号处理方法及其应用研究，E-mail：wuxinjie@lnu.edu.cn；

闫诗雨(1993-)，男，汉族，辽宁盘锦人，硕士研究生，从事电学成像、数字图像处理，控制算法等方面的研究，E-mail：meloyan1993@163.com.