航空发动机低压中介主轴多轴疲劳寿命预测

李 静，李春旺，张忠平

(1.西安电子科技大学机电学院，西安710071；2.空军工程大学理学院，西安710051)

航空发动机低压中介主轴多轴疲劳寿命预测

李 静1，李春旺2，张忠平2

(1.西安电子科技大学机电学院，西安710071；2.空军工程大学理学院，西安710051)

以航空发动机低压中介主轴为研究对象，利用ANSYS软件对低压中介主轴进行有限元分析，得到主轴不同关键截面的应力-应变。基于临界平面法，在分析原有模型损伤参量的基础上，引入最大法向应力对原有模型进行修正，并利用坐标变化原理，明确了临界平面及控制损伤参量的确定方法。在存在平均应力时，修正后的模型可直接用于材料的多轴疲劳寿命预测。在此基础上，利用修正后的多轴疲劳寿命预测模型对低压中介主轴进行寿命预测，并从危险截面位置确定和预测寿命大小方面与传统的EGD-3寿命预估法进行对比分析。结果表明：EGD-3寿命预估法预测寿命偏于保守，且预测的危险截面位置与已有试验数据不符。与之相比，利用多轴疲劳寿命预测模型可以更好地预测低压中介主轴的危险截面位置和多轴疲劳寿命。

航空发动机；低压中介主轴；多轴疲劳；有限元分析；寿命预测

1 引言

我国航空发动机经历了从测仿改型到自行研制的漫长过程，从上世纪70年代开始，以现役发动机定寿延寿和在研发动机疲劳寿命设计工作为背景，开展了发动机高、低压轴系——主轴的疲劳寿命预测方法研究。目前，国内主要利用安全寿命设计方法来确定主轴的疲劳寿命。安全寿命设计方法包括名义应力法和局部应力应变法两种，在主轴寿命计算中常用的EGD-3寿命预估法就体现了名义应力法的寿命预测思想[1]。最近，文献[2]分别利用EGD-3寿命预估法、名义应力法和应力修正系数法，对发动机主轴不同部位进行了疲劳寿命估算，发现相比于EGD-3寿命预估法及应力修正系数法，用名义应力法得到的疲劳寿命预测结果偏保守。由于发动机主轴是在复杂的多轴应力状态下工作，因此多轴疲劳失效是其最为常见的失效形式。目前，各国研究者针对多轴疲劳寿命预测方法进行了系统而深入的研究，如李静[3-4]、Fatemi[5]、Shang[6-7]、Jiang[8]、Kalluri[9]等从不同角度建立了不同的多轴疲劳寿命预测模型，但在文献中罕见利用多轴疲劳理论来预测发动机主轴的疲劳寿命。因此，基于多轴疲劳理论，进一步研究主轴疲劳寿命预测技术就显得尤为重要。

本文主要研究了某型航空发动机低压中介主轴的疲劳寿命预测问题。该型航空发动机实际工作时，低压中介主轴在工作状态下受到的主要是高/低周复合载荷，其中主循环为零—最大—零低周拉扭疲劳载荷，次循环为幅度不超过主循环幅度±5%的高周扭转疲劳载荷。由于低压中介主轴的疲劳寿命主要由其承受的主循环疲劳载荷来决定，因此文中主要研究了主循环疲劳载荷下中介主轴的多轴疲劳寿命预测问题。分析过程中，首先利用ANSYS软件对主循环载荷下低压中介主轴进行有限元分析，得到不同关键截面的应力-应变；接着结合一个修正的多轴疲劳寿命预测模型对低压轴系进行疲劳寿命预测，并与传统的EGD-3寿命预估法的预测结果进行对比分析。

2 应力-应变有限元分析

低压中介主轴的应力-应变选用有限元软件ANSYS进行分析[10]。分析过程中，选用三维20节点六面体等参元SOLID95对实体模型进行网格划分，并对所关心的缺口部位进行网格细化，划分结果如图1所示。考虑到随动强化模型可以反映材料的Bauschinger效应，且采用多线性随动强化模型数值模拟比双线性随动强化模型精度高，故在有限元计算中采用von-Mises屈服准则和多线性随动强化模型。计算过程中，中介主轴一端固定，另一端加力。为使计算的边界条件与工作状态相一致，采用力边界条件，将模型的左端面处理成固定端，六个方向的自由度全部约束。同时，为模拟实际情况，根据力等效原则，将轴向力和切向力分别加载到模型右端表面的各个节点上。根据圣维南原理，在轴的两端都加长一辅助段，使得所考察轴段不受端部加载的影响。低压中介主轴详细的有限元计算过程及结果见文献[3]。

图1 低压中介主轴有限元模型Fig.1 The finite element model of low-pressure inter-shaft

3 拉扭主循环加载下低压中介主轴的寿命预测

3.1 多轴疲劳寿命预测模型

由于低压中介主轴同时受到扭矩和轴向力的作用，且各个轴上还具有台阶、孔、槽等几何不连续部位，因此低压轴系所有关键截面都处于多轴应力-应变状态，相应地疲劳也属于多轴疲劳。对于多轴疲劳载荷下的寿命预测，基于临界平面概念的寿命预测方法越来越受到人们的重视，被普遍认为是分析多轴疲劳问题的一种比较有效的方法。李静等[4]在分析大量多轴疲劳试验数据的基础上，定义最大剪应变范围平面为临界平面，以临界平面上的最大剪应变范围 Δγmax、法向应变范围Δεn和由Ram⁃berg-Osgood关系式确定的虚法向应力范围Δσn为损伤参量，建立了一个能反映非比例附加强化现象的疲劳寿命预测模型：

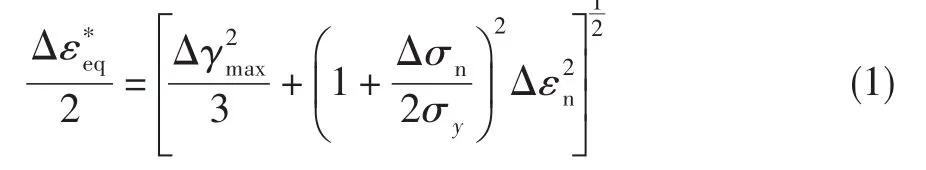
式中：σy为屈服强度。由于式(1)的控制损伤参量是虚应力范围，因此式(1)不能反映平均应力对材料疲劳寿命的影响。为考虑平均应力影响，文献[4]将式(1)修正为：

式中：σn,m为平均法向应力。

式(1)的优点是应用起来简单方便，不需要借助复杂的塑性本构方程来计算临界面上的应力参量，但模型中的虚法向应力范围和临界面上的真实法向应力范围并不相等，特别是在非比例加载下两者差距较大。虽然式(1)较好地预测了5种材料的多轴疲劳寿命[5]，但是从本质上讲式(1)本身仍然是一个经验的疲劳预测模型。为了更好地预测材料的多轴疲劳寿命，本文利用最大剪应变范围平面上的真实最大法向应力σn,max来取代式(1)中的虚法向应力范围，将式(1)修正为(MSW)：

存在平均应力时，最大法向应力可分解为法向应力幅σn,a和σn,m，即：

因此，修正后的模型本身可以反映平均应力对材料疲劳寿命的影响。结合Manson-Coffin方程，修正后的疲劳寿命计算模型为：

利用文献[5-9]中的5种材料(1045HR钢[5]、GH4169合金[6]、45钢[7]、S460N钢[8]以及Haynes188合金[9])对修正后的模型进行验证，各材料的力学和疲劳性能参数见文献[4]。验证过程中，修正模型中的应力参量利用Jiang-Sehitoglu塑性本构模型[11]进行计算。

由图2中的验证结果可见，不论是比例加载还是非比例加载，修正模型的预测值误差大都分布在2倍因子以内。这表明修正后的模型仍然可以较好地预测材料的多轴疲劳寿命，且在存在平均应力时不需要额外的修正。以本文研究的航空发动机低压中介主轴为例，由于中介主轴承受的是多轴非对称载荷，存在平均应力，因此借助有限元分析结果，修正后的模型可以更为方便地用于中介主轴的多轴疲劳寿命预测。

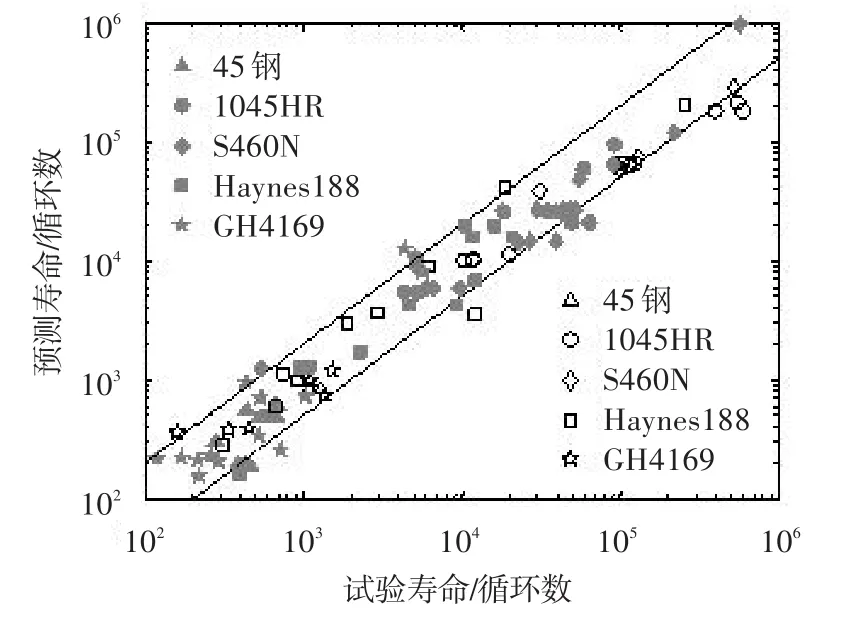
图2 试验寿命与修正模型预测值的比较(空心点为比例加载，实心点为非比例加载)Fig.2 The comparison of experimental fatigue lives and the fatigue lives predicted by the modified model(hollow dots for proportional loadings and solid dots for non-proportional loadings)

为预测低压中介主轴的疲劳寿命，截取低压中介主轴应力强度较弱的4个截面进行多轴疲劳寿命计算，其中截面1、2和4都为带孔截面，截面3为外台阶截面，如图3所示。低压中介主轴材料为40Cr3MoVA钢。由式(5)可以发现，基于临界平面法的多轴疲劳寿命预测至少包含三部分工作：①确定材料的疲劳性能参数；②确定临界面及临界面上各控制损伤参量；③预测疲劳寿命。

图3 计算截面所在的中介主轴段Fig.3 The calculated sections of inter-shaft for FEA

3.2 疲劳性能参数的确定

研究材料的疲劳寿命预测问题，通常会牵涉到4个基本疲劳性能参数——疲劳强度系数、疲劳延性系数、疲劳强度指数和疲劳延性指数。确定这4个疲劳性能参数有试验测量法与理论估算法两种，尽管试验测量结果可靠性高，但因试验设备复杂、试验过程冗长、数据处理麻烦等因素，导致材料疲劳试验数据缺乏，常希望利用材料的常规力学参量理论估算。Park等[12]利用116种钢的试验数据验证发现，Muralidharan等[13]修正的通用斜率法可以较好地预测合金钢的疲劳寿命。而文献[14]利用226种钢的试验数据进行分析发现，Roessle等[15]基于布氏硬度建立的硬度法可以较好地用来估算合金钢的疲劳性能参数。本文利用另外38种钢的试验结果[3]，分别对修正的通用斜率法和硬度法进行了验证，结果如图4所示。

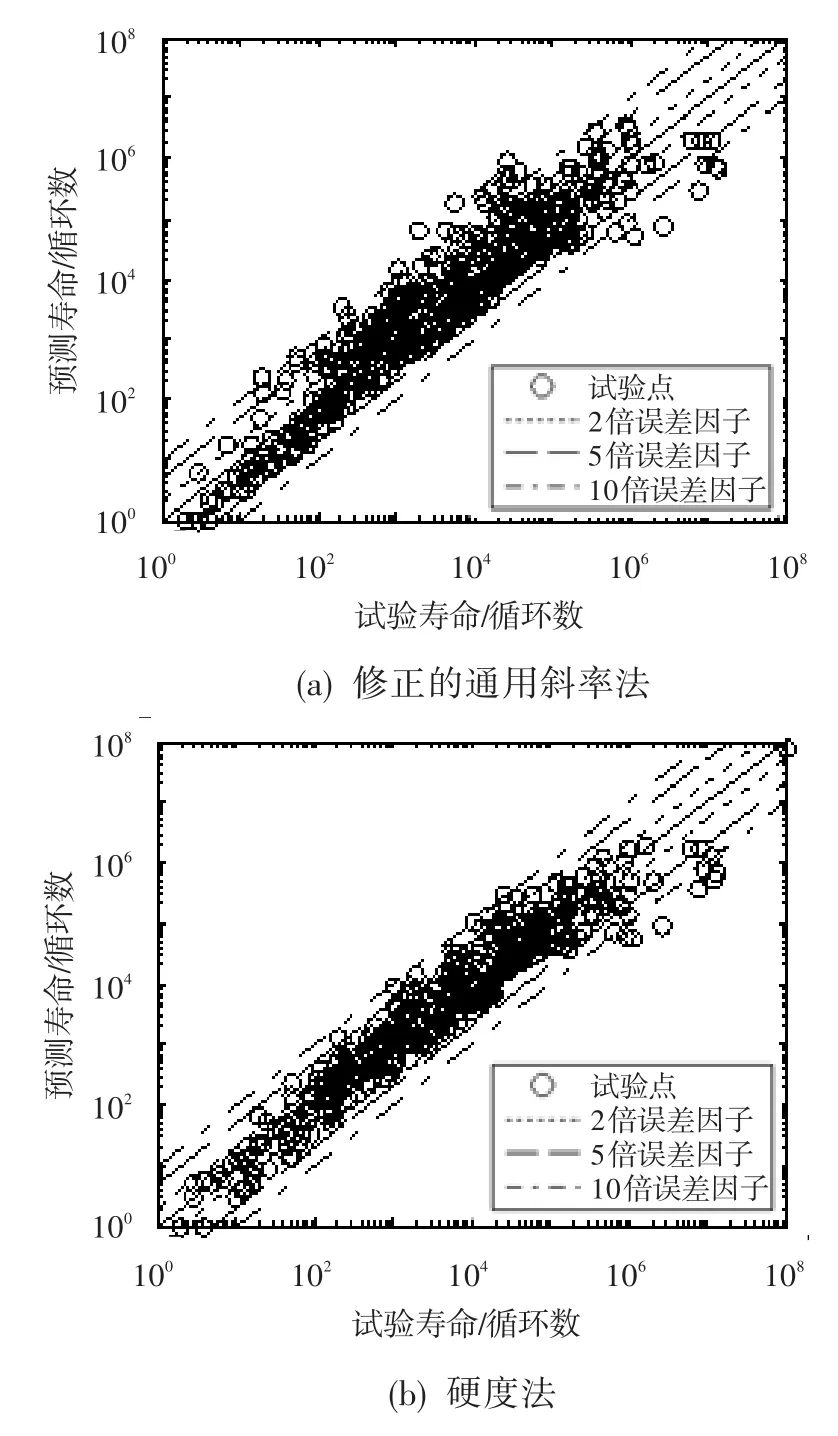
图4 试验寿命与预测寿命的比较Fig.4 The comparison of experimental fatigue lives and predicted fatigue lives

图4表明：修正的通用斜率法在高、低周疲劳范围内预测结果偏于保守一侧，而在中周疲劳范围内预测结果偏于危险；硬度法在中、低周疲劳范围内可以较好地预测钢的疲劳寿命，大部分预测结果位于5倍误差因子以内，但在高周疲劳范围内预测结果偏于保守。

综合看，与修正的通用斜率法相比，在中、低周疲劳范围内，硬度法可以更好地预测钢的疲劳寿命。因为中介主轴的预期疲劳寿命位于中、低周疲劳范围内，因此本文利用硬度法来计算40Cr3MoVA钢的各疲劳性能参数，结果见表1。硬度法的表达式为[15]：

表1 40Cr3MoVA钢的机械及疲劳性能参数Table 1 The mechanical and fatigue properties for 40Cr3MoVA

式中：HB为布氏硬度。

3.3 临界平面及控制损伤参量的确定

式(1)定义最大剪应变范围平面为临界平面，确定最大剪应变范围平面的具体步骤如下：

(1)利用有限元软件(如ANSYS)模拟试件在循环载荷下的变形，得到不同工况下危险点处的应力张量和应变张量。

(2)利用坐标变换原理(图5)得到不同工况下任意平面上的应力、应变。

式中：M为坐标变换矩阵，MT为M的转置矩阵。

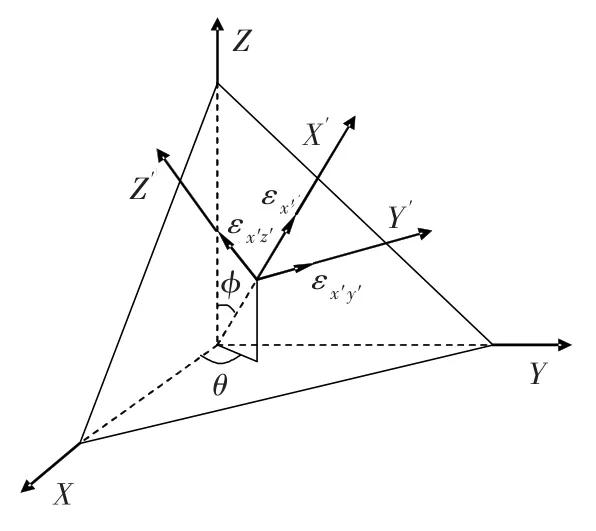
图5 任意平面的位置Fig.5 Orientation of the arbitrary plane

(3) 计算第i个平面(θi,ϕi)上的剪应变范围Δγi。

式中：q表示一个循环中离散的载荷步数。

(4)让θ在 [0°,360°)内、ϕ在 [0°,180°)内以 1°为步长变化，计算各平面上的剪应变范围。比较各平面上剪应变范围的大小，确定最大剪应变范围Δγmax的值及其所在平面的位置，然后计算所有最大剪应变平面上的法向应变范围。

(5)比较各最大剪应变平面上的法向应变范围的大小，法向应变范围最大的平面即为临界面，其位置记为(θcr，ϕcr)，然后计算(θcr，ϕcr)平面上的最大法向应力。

结合低压中介主轴的有限元计算结果，利用上述步骤计算得到低压中介主轴不同关键截面危险点处的临界平面方位，及临界面上各疲劳破坏参数的值，如表2所示。

3.4 多轴疲劳寿命的计算

将表2中不同关键截面临界面上的疲劳破坏参数值代入MSW模型(式(3))，计算得到低压中介主轴各关键截面的疲劳中值寿命(表2)。需要说明的是，MSW模型计算得到的是低压中介主轴各关键截面的理论中值寿命，为得到轴的理论安全寿命，需要除以寿命安全系数。文献[16]建议材料的寿命安全系数取为5，以保证结构的可靠性。如果低压中介主轴的寿命安全系数也取为5，则从表2中列出的理论安全寿命结果可看出，截面1为低压中介主轴的最危险截面，其理论安全寿命为19 680个标准循环。

表2 低压中介主轴各截面控制损伤参量及寿命预测结果Table 2 The damage parameters and predicted lives for the different sections of low-pressure inter-shaft

3.5 EGD-3寿命预估法

为便于对比分析，进一步利用EGD-3寿命预估法[1]计算了低压中介主轴不同关键截面的理论安全寿命。EGD-3寿命预估法的基本思想就是对于选定的关键截面，由给定应力下的扭转疲劳缺口系数对其缺口处的名义应力进行修正，然后将设计寿命下的交变应力转换成当量稳态剪应力，并与材料的当量弹性剪切强度进行比较，从而确定强度储备系数。如果强度储备系数大于1.4，则主轴的理论安全寿命大于106个标准循环，反之主轴的理论安全寿命小于106个标准循环。此时，主轴的理论安全寿命可由下式计算得到：

式(14)、式(15)中：τeq为 Mises-Hencky当量剪应力，τb2为当量弹性剪切强度，α6为106标准循环对应的扭转疲劳缺口系数，τ-1,7为修正的107对称循环扭转疲劳强度，N为理论安全寿命。

详细的计算方法与步骤可见文献[1]。利用EGD-3寿命预估法[1]计算得到的理论安全寿命也列于表2中。可见，截面3为低压中介主轴的最危险截面，其理论安全寿命为14 521个标准循环。

3.6 对比分析

从表中数据可以发现，两种方法预测低压中介主轴的最危险截面不同，多轴疲劳理论预测的最危险截面为1截面(带孔截面)，而EGD-3寿命预估法预测的最危险截面为3截面(外台阶截面)。文献[17]对低压主轴进行疲劳试验后发现，5根被试轴疲劳破坏的位置均位于通油孔处。这说明对于低压主轴，带孔截面比外台阶截面更易于破环，因此本文通过多轴疲劳理论预测的低压中介主轴最危险截面为1截面比EGD-3寿命预估法预测的最危险截面为3截面更具合理性。

另外，该型发动机低压轴系最新给定的安全寿命为18 000个标准循环，这与利用MSW模型计算得到的理论安全寿命(19 680个循环)十分接近，这从另一方面说明了多轴疲劳理论预测低压中介主轴疲劳寿命的正确性。与之相比，利用EGD-3寿命预估法计算得到的低压轴系的理论安全寿命(14 521个循环)偏于保守。

4 结论

(1)多轴拉扭疲劳加载下，该型航空发动机中介主轴的最危险截面位于靠近压气机后轴端部的带孔截面处，这与已有试验结果的疲劳破环位置相符。与之相比，EGD-3寿命预估法预测的危险截面位于外台阶截面处，与已有试验结果不符。

(2)在已有模型的基础上，建立了一个统一的多轴寿命预测模型，新模型可直接用于存在平均应力加载情况下的多轴疲劳寿命预测。

(3)与该型发动机低压轴系最新给定的安全寿命18 000个标准循环相比，利用EGD-3寿命预估法预测理论安全寿命为14 521个循环偏于保守，而利用多轴疲劳寿命预测模型预测理论安全寿命为19 680个循环更为合理。

(4)对于合金钢，与修正的通用斜率法相比，硬度法可以更好地估算材料的疲劳性能参数。结合硬度法，仅仅需要材料的基本力学性能参数，就可以利用多轴疲劳寿命预测模型对低压中介主轴进行疲劳寿命预估，便于工程应用。

[1]EGD-3斯贝MK202发动机应力标准[S].丁爱祥，吴君，译.北京：国际航空编辑部，1979.

[2]陆 山，陈 倩，陈 军.航空发动机主轴疲劳寿命预测方法[J].航空动力学报，2010，25(1)：148—151.

[3]李 静.金属材料的多轴疲劳寿命预测模型及其应用[D].西安：空军工程大学，2012.

[4]李 静，孙 强，李春旺，等.一种新的多轴疲劳寿命预测方法[J].机械工程学报，2009，45(9)：285—290.

[5]Fatemi A，Socie D F.A critical approach to multiaxial fa⁃tigue damage including out-of-phase loading[J].Fatigue and Fracture of Engineering Materials and Structures，1988，11(3)：149—165.

[6]Shang D G，Sun G Q，Yan C L，et al.Creep-fatigue life prediction under fully-reversed multiaxial loading at high temperatures[J].International Journal of Fatigue，2007，29：705—712.

[7]Shang D G，Sun G Q，Deng J，et al.Multiaxial fatigue dam⁃age parameter and life prediction for medium-carbon steel based on the critical plane approach[J].International Jour⁃nal of Fatigue，2007，29：2200—2207.

[8]Jiang Y Y，Hertel O，Vormwald M.An experimental evalu⁃ation of three critical plane multiaxial fatigue criteria[J].International Journal of Fatigue，2007，29：1490—1502.

[9]Kalluri S，Bonacuse P J.In-phase and out-of-phase axi⁃al-torsional fatigue behavior of Haynes 188 at 760℃[R].NASA TM-105765，1991.

[10]李 静，孙 强，李春旺，等.某型航空发动机压气机叶片振动疲劳寿命研究[J].应用力学学报，2011，28(2)：189—193.

[11]Jiang Y，Sehitoglu H.Modeling of cyclic ratcheting plastic⁃ity,Part I:Development of constitutive/Part II:Compari⁃son of model simulations with experiments[J].ASME Trans.J.Eng.Mater.Tech.，1996，63：720—733.

[12]Park J H，Song J H.Detailed evaluation of methods for es⁃timation of fatigue properties[J].Int.J.Fatigue，1995，17：365—373.

[13]Muralidharan U，Manson S S.A modified universal slopes equation for estimation of fatigue characteristics of metals[J].ASME Trans.J.Eng.Mater.Tech.，1988，110：55—58.

[14]Hariharan K，Prakash R V，Sathya P M.Weighted error criterion to evaluate strain-fatigue life prediction methods[J].Int.J.Fatigue，2011，33：727—734.

[15]Roessle M L，Fatemi A.A strain-controlled fatigue proper⁃ties of steels and some simple approximations[J].Int.J.Fa⁃tigue，2000，22：495—511.

[16]朱梓根，刘廷毅，陈 光，等.航空涡喷、涡扇发动机结构设计准则(研究报告)：第六册—转子系统[M].北京：中国航空工业总公司发动机系统工程局，1997.

[17]唐平宣.某系列发动机高压涡轮轴失效分析及改进措施的探讨[J].科技与实践，2005，(3)：94—97.

Multi-axial fatigue life prediction for aero-engine low-pressure inter-shaft

LI Jing1，LI Chun-wang2，ZHANG Zhong-ping2
(1.School of Mechano-Electronic Engineering，Xidian University，Xi’an 710071，China；2.The Science Institute，Air Force Engineering University，Xi’an 710051，China)

Taking aero-engine low-pressure inter-shaft as the research object,the stress-strain states of the key sections of the low-pressure inter-shaft were calculated by using the ANSYS software.A recently proposed multi-axial fatigue life prediction model was modified on the basis of the critical plane approach.The orientation of the critical plane and the damage parameters of the modified model were determined by using the coordinate transformation principle.The modified model was able to directly estimate the fatigue life of material when the mean stress was existed.And then the fatigue life of the low-pressure inter-shaft was predicted by using the modified multiaxial fatigue life prediction model.The predicted results of the critical location and fatigue life are contrasted with the results of the EGD-3-based life prediction method.The results showed that the predicted life of EGD-3 method was conservative and the critical location was unreasonable.In contrast to the EGD-3-based life prediction method,the modified multi-axial fatigue life prediction model could offer reasonable life prediction and critical location.

aero-engine；low-pressure inter-shaft；multi-axial fatigue；finite element analysis；life prediction

V235.1

A

1672-2620(2017)05-0031-05

2016-12-09；

2017-10-04

国家自然科学基金(51601221，51575524)；陕西省自然科学基础研究计划(2015JM5240)

李 静(1985-)，男，河北赞皇人，讲师，博士，主要研究方向为航空金属材料的疲劳与断裂。