航空发动机端面密封装置中O形密封胶圈的滑动摩擦力分析
2017-11-23徐鹏飞李贵林
徐鹏飞,贺 耀,李贵林,宋 飞
(中国航发四川燃气涡轮研究院,成都610500)
航空发动机端面密封装置中O形密封胶圈的滑动摩擦力分析
徐鹏飞,贺 耀,李贵林,宋 飞
(中国航发四川燃气涡轮研究院,成都610500)
简要介绍了三种用于航空发动机附件传动机匣轴端滑油密封的端面密封装置中O形密封胶圈滑动摩擦力计算方法——Lindley算法、经验公式和Parker公司算法,提出了一种与实际装配情况相同的径向受压缩的O形密封胶圈有限元建模及滑动摩擦力计算方法。通过对同一套端面密封装置的O形密封胶圈滑动摩擦力进行的计算结果表明,有限元计算与经验公式的结果非常接近,Lindley算法结果偏小,而Parker公司算法结果偏高。
航空发动机;传动机匣;端面密封;O形密封胶圈;滑动摩擦力;有限元
符号表
bO形密封胶圈压缩后椭圆截面的短轴尺寸/m
CO形密封胶圈的压缩率
C10、C01橡胶材料的Mooney-Rivlin力学性能常数/MPa
DO形密封胶圈自由状态下的内直径/m
D2孔用O形密封胶圈的安装孔直径/m
Db动密封用O形密封胶圈的滑动直径/m
dO形密封胶圈的断面直径/m
E材料的杨氏模量/MPa
FO形密封胶圈对轴的压缩力/N
fO形密封胶圈滑动时的摩擦力/N
G材料的切变模量/MPa
HO形密封胶圈材料的邵氏硬度
hO形密封胶圈的安装槽深度/m
I1、I2应力张量的第一、第二不变量
LO形密封胶圈中径所在直径的周长/m
W应变能函数
αO形密封胶圈的拉伸率
μ滑动摩擦系数
σi(i=1,2,3)O形密封胶圈在3个方向的主应变
1 引言
在航空发动机和飞机的附件传动机匣中,轴端的滑油密封常采用弹簧加载或磁力加载的端面密封装置。弹簧加载端面密封装置中,O形密封胶圈的滑动摩擦力影响整个端面密封组件中的端面接触比压,进而影响摩擦副的[PV]限制值(密封面的接触比压与滑动线速度的乘积)和摩擦功率的计算,以及影响密封环的轴向随动性。而磁力端面密封装置中,O形密封胶圈的滑动摩擦力影响到密封环的轴向随动性,且O形密封胶圈与转轴的摩擦扭矩需要大于磁性静环与磁性动环上石墨密封环之间的摩擦扭矩。因此,O形密封胶圈摩擦力的准确计算对整个端面密封结构的设计很重要。因附件传动机匣的温度一般不超过200℃,所以这些端面密封装置中通常使用橡胶材料的O形密封胶圈。
为研究O形密封圈在直线往复运动过程中所受到的摩擦力,首先需要研究O形密封圈和接触表面之间产生的接触压力。较早的有Lindley提出的O形密封胶圈在小压缩情况下单位长度上的载荷分布计算公式,但该公式仅在较小压缩率作用下与实验吻合,随着压缩率的增加,理论计算的压缩作用力较实验值逐渐偏小[1-2]。近森德重[3]通过对实验数据的拟合,给出了O形密封胶圈压缩作用力计算的经验公式,但未给出实验的进一步细节,也未对公式的拟合方法进行说明。Parker公司的产品手册中给出了O形密封胶圈压缩率与滑动摩擦力的对应关系曲线[4],但仅列出了橡胶材料邵氏硬度为70、80、90的情况,同时仅对滑动表面的粗糙度提出要求,未给出摩擦系数。而国内航空发动机传动机匣轴端密封装置用的氟橡胶FX-4材料的O形密封胶圈的邵氏硬度仅为58~68,因此在设计时不能直接使用Parker公司的结果。
随着有限元计算方法和软件的发展,陈国定[5]、谭晶[6]、张婧[7]、李双喜[8]等先后借助有限元软件对O形密封胶圈的压缩进行了分析,但重点都是在应力场,且都是对O形密封胶圈安装槽的壁面施加径向的强迫位移,这与实际装配情况有很大差异。为此,本文提出一种与实际装配情况相同的径向受压缩的O形密封胶圈有限元建模及滑动摩擦力计算方法,并与Lindley算法、经验公式算法及Parker公司算法进行了对比分析。
2 端面密封装置结构
航空发动机附件传动机匣轴端的端面密封装置结构如图1所示。O形密封胶圈在直线往复运动过程中所受到的摩擦力及胶圈和接触表面之间的接触压力,与其两侧介质压差作用力有关。因航空发动机和飞机附件传动机匣的轴端密封装置工作时密封介质两侧的压力差较小(一般在10kPa左右),所以本文不考虑密封装置两侧密封介质的压力差对胶圈滑动摩擦力的影响,仅考虑O形密封胶圈受径向压缩作用后产生的径向压力所引起的滑动摩擦力。

图1 端面密封装置结构简图Fig.1 The structure of mechanical face seal
3 O形密封胶圈滑动摩擦力计算方法
Lindley算法和经验公式算法均是先计算出胶圈的压缩作用力,然后根据式(1)计算出滑动摩擦力。O形密封胶圈滑动摩擦系数与胶圈表面和滑动轴表面的粗糙度有关,粗糙度越大,摩擦系数越高;但粗糙度过小时,由于分子间结合力使得摩擦系数也较高。文献[9]实测了O形密封胶圈与轴之间在有滑油润滑状态下的摩擦系数,在0.071 9~0.075 9范围。对于航空发动机附件传动机匣轴端密封装置处的O形密封胶圈,因润滑油较少,处在滑油和空气混合物的介质中,本文建议该种状态的滑动摩擦系数取0.15。

3.1 Lindley算法
Lindley在实验研究中使用了天然橡胶,其结果与Hertz接触理论的O形密封胶圈小压缩理论相符。Lindley算法计算公式[2]如下:

O形密封胶圈的分析简图如图2所示。

图2 O形密封胶圈分析简图Fig.2 Dimensions of the O-ring rubber seal
在HB 4-56~57-1987中对用于活动密封的O形密封胶圈要求为:分模面为45°,安装密封圈的矩形槽的表面粗糙度不低于Ra0.8μm。
橡胶材料的杨氏模量与邵氏硬度有关[10]。文献[10]和[11]中相同邵氏硬度的橡胶,其杨氏模量和剪切模量并不相同,有微小差异。因文献[10]未给出橡胶材料的Mooney-Rivlin力学性能常数,所以本文选用文献[11]给出的参数,具体对应关系见表1。
3.2 经验公式算法
[3]、[12],O形密封胶圈压缩率与总压缩作用力之间的关系可表示为:

目前航空发动机中端面密封装置用的O形密封胶圈采用的是氟橡胶材料FX-4,根据材料标准,其邵氏硬度为63±5。
3.3 Parker公司算法
Parker公司的产品手册中仅给出了邵氏硬度为70、80、90的三种胶圈的滑动摩擦力与压缩率的关系(图3[4])。而氟橡胶FX-4的邵氏硬度为63±5,因此选用Parker公司邵氏硬度为70的O形密封胶圈进行摩擦力估算。

表1 橡胶材料的邵氏硬度与力学性能常数[11]Table 1 IRHD and mechanics of rubber material
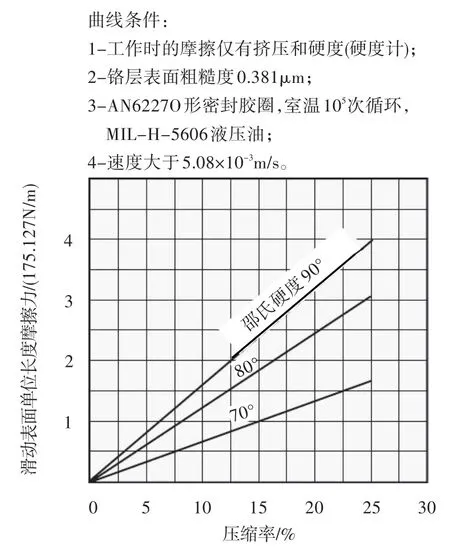
图3 Parker公司的O形密封胶圈摩擦力与压缩率关系曲线[4]Fig.3 The change of friction force with O-ring compression rate of Parker Corporation
需注意,Parker公司算法并不含摩擦系数一项,而是针对滑动摩擦表面粗糙度为0.381 μm。因此结构设计时,需将端面密封装置中O形密封胶圈沿金属件表面滑动时的表面粗糙度设计为Ra0.4 μm。
3.4 有限元计算方法
用有限元方法计算胶圈摩擦力的基本思路,是先计算出胶圈在滑动面上因压缩而产生的正压力,然后借助滑动摩擦系数即可求出滑动摩擦力。
采用氟橡胶FX-4的O形密封胶圈主体为橡胶,橡胶结构的应力应变关系是一个复杂的非线性函数,需用应变能函数表示,广泛采用Mooney-Rivlin函数[10],其杨氏弹性模量和Mooney-Rivlin力学性能常数与胶圈的邵氏硬度对应关系见表1。

有限元计算时采用ANSYS软件,轴对称模型,O形橡胶密封圈、安装槽和内轴均选用平面单元PLANE183。
由于O形密封胶圈拉伸时的体积不变性(由文献[10]可知,橡胶材料的泊松比通用值为0.499 7,且在大多数应用中足够准确),属于大变形,因此对自由状态的胶圈进行建模。考虑内轴上有一装配引导角,几何模型及边界条件如图4所示。

图4 计算O形密封胶圈正压力的有限元模型Fig.4 FEM model of calculated O-ring compression force
因O形密封胶圈装配前后变形较大,其初始的圆形边界在装配后的变形无法预估,所以本文采用点-面接触[13],选用接触单元CONTA172和目标单元TARGE169配对组成。共建立胶圈外表面节点与胶圈槽壁面、胶圈外表面节点与内轴壁面两个接触对。
分析时,需将O形密封胶圈外表面节点与胶圈槽壁面接触对设置为“闭合间隙”条件。O形密封胶圈在径向受到压缩后的应力云图如图5所示。
4 四种算法计算结果对比
以某一端面密封装置中的滑动密封用O形密封胶圈的实际安装尺寸(表2)为例,应用上述四种计算方法计算其滑动摩擦力,结果见表3。从表中可看出,经验公式和有限元的计算结果相差较小,仅相差0.53%;Lindley算法的计算结果偏低,这与Lindley通过实验发现的理论计算值低于实验值相一致[2];Parker公司算法结果偏高,这是由于该算法是将胶圈的邵氏硬度取为70,而另外两种算法中胶圈的邵氏硬度是根据材料标准取为63。同时,根据经验公式可知,摩擦力与硬度值的4.5次方成正比,因此硬度值越高摩擦力越大。

图5 O形密封胶圈应力图Fig.5 The stress of O-ring rubber seal

表2 某端面密封装置中的O形密封胶圈安装尺寸Table 2 Sizes of an O-ring rubber seal in a mechanical face seal

表3 四种算法计算的胶圈滑动摩擦力对比Table 3 Friction force calculated with four kinds of arithmetic
5 结论
(1)本文给出的有限元模型和引用的橡胶材料的力学性能参数可以准确计算O形密封胶圈的滑动摩擦力。
(2)为降低O形密封胶圈滑动表面的摩擦系数,其滑动表面的粗糙度应控制在Ra0.4 μm范围内,该粗糙度对应的滑动摩擦系数在0.15左右;若滑动表面的粗糙度大于Ra0.4 μm,则滑动摩擦系数会增加。
(3)经验公式和有限元方法结果最为接近,均可用于计算O形密封胶圈的滑动摩擦力。
(4)本文给出的有限元计算的单元类型和引用的橡胶材料的力学性能参数,同样可用于异形密封胶圈(如椭圆形和X形)的接触压力计算。
参考文献
[1]George A F,Strozzi A,Rich J I.受压无约束弹性O形圈密封的应力场及计算机预测值与实验结果的比较[C]//.国际流体密封会议论文集.北京:机械工业出版社,1991:55—67.
[2]Lindley P B.Load-compression relationships of rubber units[J].Journal of Strain Analysis for Engineering Design,1966,1(190):190—195.
[3]近森德重.密封元件-O形密封圈[M].朱仁杰,译.北京:机械工业出版社,1976:104—109.
[4]Parker Hannifin Corporation O-Ring Division.Parker O-ring handbook[K].50thAnniversary Edition.
[5]陈国定,Haiser H,Haas W,等.O形密封圈的有限元力学分析[J].机械科学与技术,2000,19(5):740—742.
[6]谭 晶,杨卫民,丁玉梅,等.O形橡胶密封圈密封性能的有限元分析[J].润滑与密封,2006,31(9):65—69.
[7]张 婧,金 圭.O形密封圈接触压力的有限元分析[J].润滑与密封,2010,35(2):65—69.
[8]李双喜,蔡纪宁,张秋翔,等.机械密封补偿机构中辅助O形密封圈的性能分析[J].摩擦学学报,2010,30(3):308—314
[9]陈聪慧.航空发动机机械系统常见故障[M].北京:航空工业出版社,2013:335—349.
[10]弗雷克利P K,佩恩A R.橡胶在工程中应用的理论与实践[M].杜承泽,唐宝华,罗东山,等,译.北京:化学工业出版社,1985.
[11]Warner B.Analyzing hyperelastic materials w:some practi⁃cal considerations[EB/OL].www.impactengsol.com.
[12]奚 翠.密封装置设计基础[M].合肥:安徽科学技术出版社,1987.
[13]Nakasone Y,Yoshimoto S,Stolarski T A.Engineering analysis with ANSYS software[M].Elsevier Butter⁃worth-Heinemann,2006.
Sliding friction force of O-ring in aero-engine mechanical face seal
XU Peng-fei,HE Yao,LI Gui-lin,SONG Fei
(AECC Sichuan Gas Turbine Establishment,Chengdu 610500,China)
To calculate the sliding friction force of O-ring in mechanical face seal of gear box in aero-en⁃gine,three formulas,Lindley formula,empirical approach,and Parker corporation method were presented.A FEM model and sliding friction force calculation method of radial compressed O-ring were proposed ac⁃cording to the actual situation in the mechanical face seal.The sliding friction force of the O-ring from the same set of face seal was calculated.The results show that the friction force with empirical approach and fi⁃nite element method are very similar;the result of Lindley formula is relative low,and the Parker corpora⁃tion method is relative large.
aero-engine;gear box;mechanical face seal;O-ring;sliding friction force;finite element method
V233.4
A
1672-2620(2017)05-0058-05
2016-06-16;
2017-09-02
徐鹏飞(1983-),男,云南陆良人,工程师,主要从事航空发动机密封装置设计工作。
