基于贝叶斯的金融时间序列预测研究
2017-11-22叶静
叶 静
基于贝叶斯的金融时间序列预测研究
叶 静
传统的时间序列分析与预测方法没有考虑样本和参数的先验信息,导致预测结果和实际数据的偏差较大,贝叶斯参数估计方法可以充分利用参数的先验信息,使得估计参数的方差更小,估计结果更加精确,预测结果更真实有用。随着MCMC方法和WinBUGS软件的发展,贝叶斯分析方法估计模型的计算困难逐渐减弱,因此,近年来贝叶斯时间序列预测方法越来越受到关注。本文基于上证指数收盘价的数据,采用Eviews和 WinBugs软件,对样本数据进行预处理,利用贝叶斯参数估计方法进行时间序列自回归模型的实证研究分析。
自回归模型;贝叶斯参数估计;MCMC方法
在现实经济生活中,根据经济过程所表现出来的规律性对经济序列未来发展趋势进行研究,可以对未来经济活动有所了解,捕捉经济特点,为政府和企业提供经济决策。由于经济系统存在惯性,随着时间推移经济系统变量之间常常存在一定的相关关系,因此,时间序列分析和预测方法在经济预测问题中运用普遍。金融时间序列数据比较复杂,常常呈现出较强的非平稳性和长记忆性。传统时间序列分析方法对于捕捉金融时间序列数据的这种复杂特性准确度不高,所作预测偏差也较大。尤其在对模型进行参数估计的过程中,由于经济序列通常不能满足基本假定条件,导致模型的估计结果不准确,从而模型的预测也失效。且传统时间序列预测法不能避免自由度不足的问题、由于参数过多而要求样本容量足够大的问题以及无法重复实验检验模型预测好坏的问题。1986年Litterman 在其《Forecasting with bayesin vector autoregressions--five years of experience》一文中首次将贝叶斯方法运用到时间序列模型预测分析中[1],和传统的参数估计方法相比,贝叶斯时间序列分析方法考虑到人们的经验知识,并将其作为先验信息,在此基础上,结合模型结构、样本信息对时间序列数据进行分析和预测,由于充分利用样本和参数的先验信息,使得估计结果具有更小的方差或标准误差,估计值的有效性较高,从而模型的预测精度也随之上升。鉴于此,本文在实际数据上用贝叶斯参数估计法对道琼斯工业指数时间序列进行估计,以得到更精确的时间序列模型。
1 AR(p)模型的估计方法
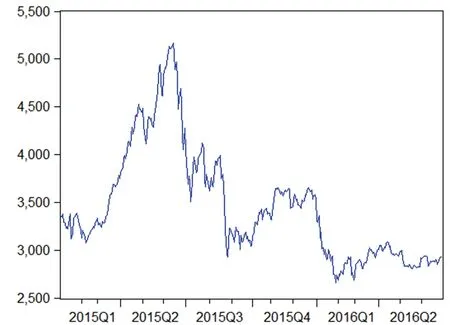
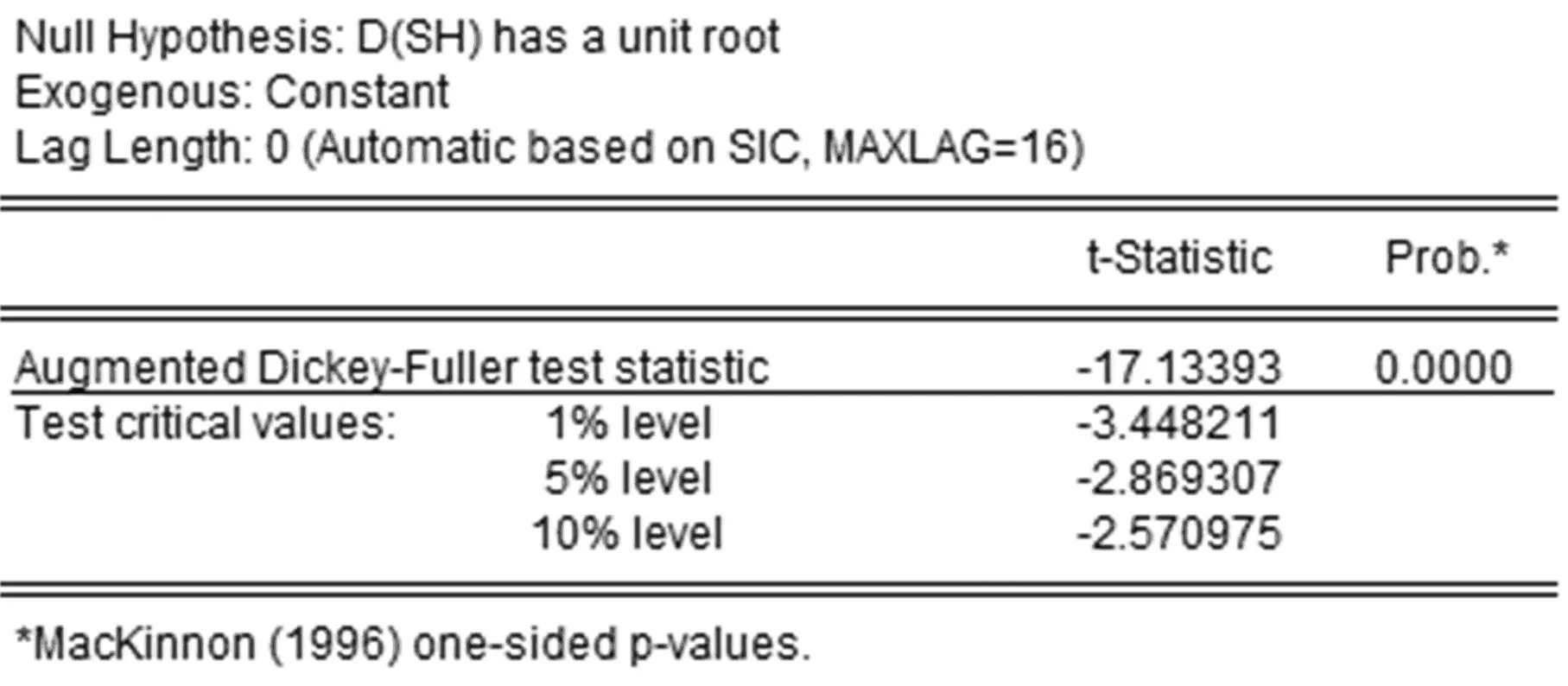
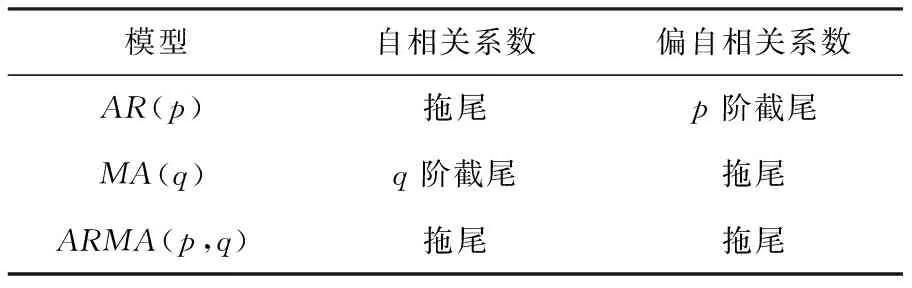
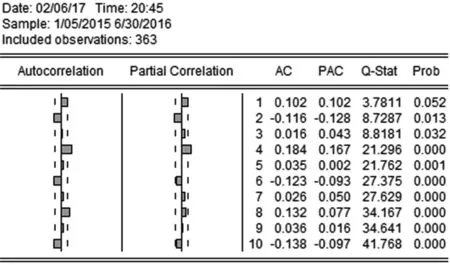
AR(p)模型:如果一个系统的最高阶数为p,随机扰动项与过去序列值不相关,即有E(xsεt)=0,s xt=β0+β1xt-1+β2xt-2+…+βpxt-p+εt AR(p)模型贝叶斯估计: 令A= 故上式的矩阵表示为: (2)通过第一步的分析发现,似然函数L(β,τ)同于正态-伽马分布密度函数核的形式,即在给定τ的情况下,β的先验分布为正态分布,而τ的先验分布为gamma分布,则β,τ的联合分布为P(β,τ)=P(β|τ)P(τ)[3] 其中 (3)由贝叶斯公式: P(β,τ|X)∝P(β,τ)L(β,τ) (β-2(A+Q)-1(C+Qu) 令A*=(A+Q),C*=C+QU,C*TA*-1C*=(A*-1C*)TAA*-1C*(A是对称的) 令 得D>0 (4)参数β的边际后验分布密度函数为: 上式具有多元t分布密度函数核的结构形式,自由度为n+2α,位置参数为A*-1C*,精度矩阵为(n+2α)A*-1D,即 β|X~Mtp(n+2α,A*-1C*,(n+2α)A*-1D) 类似的,我们得到参数τ的边际后验分布式为: 本文选取2015年1月5日到2016年6月30日的上证指数收盘价作为研究对象,一共364个样本。 在做时间序列数据分析时,应先检验数据的平稳性,通过eviews做出时序图(图2.1),可以发现数据没有围绕某个平均值上下波动,初步判定序列不平稳。 图1 上证指数收盘价格时序图 进一步通过ADF检验,结果如表1。 表1收盘价序列单位根检验结果 结果表明,在1%,5%,10%的显著水平下,ADF的检验值分别为-3.448,-2.869,-2.571均小于显著水平值-1.23,且p值0.6623大于5%,因此检验不通过,序列为非平稳的。 因此对序列进行一阶差分,差分后进行ADF检验,结果如表2.2,表现为平稳的序列。 表2 一阶差分序列单位根检验 常用时间序列模型的构造,通过自相关系数和偏自相关系数表现形式判断,如表2.3。 表3 常用时间序列分析方法 画出一阶差分后序列的自相关,偏自相关图(图2) 图2 一阶差分序列的自相关,偏自相关图 通过观察,该序列的ACF和PACF可以发现,ACF具有拖尾性,而PACF在2阶后截尾,根据AIC准则得到适合的模型为AR(2)模型: Yt=θ1Yt-1+θ2Yt-2,t=2,3,…364 以p(τ)∝1/τ为模型精度参数的先验分布形式。由于{εt}~N(0,δ2),若δ2=0,则模型精度参数的先验分布设置可能不合理,从而会导致参数的后验分布存在问题。在实际应用中,取具体的参数先验分布如下[4-6]: T~Gamma(1.0E-3,1.0E-3), θ1|τ~N(0.01,1.0E-6), 为了能够快速计算出贝叶斯估计,进行高效的迭代运算,采用MCMC方法[7-8],并运用WinBUGS软件包画出AR(2)模型贝叶斯分析的Doodle图如下: 表3 AR(2)模型WinGUGS运行结果 参数均值方差2.5%中位数97.5%开始样本tau1.421E-41.099E-51.217E-41.419E-41.635E-4111000theta[1]1.1322.9870.99731.1011.205111000theta[2]-0.13323.077-0.2054-0.10150.002133111000 为了使模型参数达到平稳状态[9],我们先设置1000次Gibbs预迭代,然后在丢弃预迭代的基础上(降低起始值的影响),再进行10000次Gibbs迭代,则WinBUGS运行结果是从第1001次开始到第10000次,见表2.3,可以看出θ1,θ2,τ的均值分别为1.132,-0.1332和1.421E-4,且θ1,θ2,τ的95%置信区间分别为(0.9973,1.205),(-0.2054,-0.1015)和(1.217E-4, 1.635E-4)。且参数后验分布图为图2.3,图2.4及图2.5。 并且通过对初始值分别进行11000次迭代分析,来检验参数的收敛性。可以看出,参数链的轨迹具有重合倾向,因此,参数收敛。 实际值与拟合值图如下,可以看出拟合效果很好。 图4 τ后验分布图 图5 theta[1]后验分布图 图6 theta[2]后验分布图 图7 tau的链轨迹 图8 theta[1]的链轨迹 图9 theta[2]的链轨迹 图10 蓝线表示实际值,红线表示拟合值 本文根据时间序列AR模型的条件似然函数构造了模型参数的先验分布函数,并将贝叶斯估计方法引入参数估计中,由于贝叶斯方法估计较为困难,运用MCMC方法和WinBUGS软件对金融时间序列模型进行估计,使得贝叶斯方法引入时间序列模型的参数估计的应用更加简单,可以弥补传统估计方法的不足,充分考虑参数先验信息,从而使得建模过程中对历史数据的信息提取更加完整,从而模型的拟合效果也会大大提高。 [1] Litterman R B.Forecasting with bayesin vector autoregressions--five years of experience[J]Journal of Business&Economic Statistics,1986,4(1):25-37. [2] 郑进城,朱慧明.基于 MCMC 方法的贝叶斯 AR(P)模型分析[J].统计与决策,2005(10):4-6. [3] 朱慧明,韩玉启,郑进城.基于正态一Gamma共轭先验分布的贝叶斯AR(p)预测模型[J].统计与决策,2005(1):8-9 . [4] 郑进城,朱慧明.基于MCMC方法的贝叶斯AR(p)模型分析[J].统计与决策,2005(10):4-6 [5] 刘乐平.基于 WinBUGS 软件的贝叶斯计量经济学[J].东华理工学院学报,2007,(2). [6] 朱慧明,刘智伟,时间序列向量自回归模型的贝叶斯推断理论[J].统计与决策,2004(1):11-12. [7] 张尧庭,陈汉峰编著.贝叶斯统计推断[M].北京:科学出版社,1991. [8] Press J s.贝叶斯统计学[M].北京:中国统计出版社,1999. [9] 马跃渊,徐勇勇,郭秀娥.MCMC收敛性诊断的方差比法及其应用[J].中国卫生统计,2004,21f2):154.156. [10] 刘乐平,袁卫.现代贝叶斯分析与现代统计推断[J].经济理论与经济管理,2004(6):23-27. [11] 李子奈等. 计量经济 学: 第二版 [M]. 北 京: 高 等教育出版社, 2005: 9-16. OntheFinancialTimeSeriesPredictionBasedonBayesian Ye Jing The traditional time series analysis and prediction method does not take the prior information of the samples and parameters, which leads to the large deviation between the prediction results and the actual data. However the Bayesian method can make full use of the prior information of the parameters, so that the variance of estimated parameters is much small, the results are more accurate, the forecast is more realistic and useful. With the development of MCMC method and WinBUGS software, the Bayesian time series prediction method has been paid increasingly attention in recent years. Based on the data of Shanghai Composite Index, this paper used Eviews and WinBugs softwares to preprocess the sample data and analyze the time series autoregressive model by Bayesian parameter estimation method. autoregressive model; Bayesian parameter estimation; MCMC method F224 A 1673-1794(2017)05-0055-04 叶静,滁州学院数学与金融学院助教,硕士(安徽 滁州 239000) 滁州学院校级规划项目(2015GH34) 2017-04-23 责任编辑:刘海涛

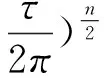
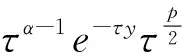
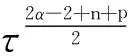
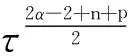




2 实证分析






3 总结
