双凹摩擦摆隔震烟风道结构地震响应1)

冯若愚 陈 瑛王 辉 柏 洁

(山东大学土建与水利学院，济南250061)

双凹摩擦摆隔震烟风道结构地震响应1)

冯若愚 陈 瑛2)王 辉 柏 洁

(山东大学土建与水利学院，济南250061)

传统烟风道板式滑动支座可减少道体热胀冷缩时的摩擦阻力，但抗震耗能能力不足，缺少变形后的复位能力，且会约束道体的转动而可能导致结构破坏.将摩擦摆隔震支座用于烟风道，可同时具有热滑移、隔震功能，允许道体在温度作用下自由转动.本文对烟风道采用双凹摩擦摆中间隔震的结构体系地震响应进行了研究,建立了横向地震作用下简化的三自由度地震响应分析模型，其中双凹摩擦摆采用三线性滞回模型，推导了一阶状态空间微分运动方程.该模型的分析结果与有限元实体模型分析结果非常接近.利用简化模型研究了不同场地类别、不同强度地震激励作用下双凹摩擦摆的恢复力特点及隔震效果，结果表明：与非隔震结构相比，双凹摩擦摆隔震的烟风道的道体反力、支架剪力均得到了控制.

隔震，烟风道，双凹摩擦摆，三线性滞回模型

随着机组容量的加大，火力发电厂烟气流量加大，道体截面尺寸也非常大，如某600MW机组工程，主烟道截面尺寸6.0m×11m；某1000MW机组工程，主烟道截面尺寸 7.5m×12.0m.烟道内部积灰面积可达管道截面面积的1/4.地震作用下，道体会产生很大的惯性力而造成结构破坏.传统烟风道设计为了降低管道热位移的摩擦阻力，通常在支墩(架)和道体间设板式滑动支座.板式滑动支座无隔震耗能能力，缺少位移后的自复位能力，且会约束道体的转动而可能导致结构破坏.本研究将摩擦摆隔震支座用于烟风道，可以同时具有减少摩擦力和隔震功能，允许道体在温度作用下在支座上自由转动.目前，还没有针对烟风道支座隔震方面进行的研究.

常用的摩擦摆隔震支座有单凹摩擦摆和双凹摩擦摆.双凹摩擦摆已经用于日本的建筑[1]和桥梁结构[2].Tsai等[3]发现双凹摩擦摆两个滑移面摩擦系数不等时，其滞回曲线为三线性.Constantinou[4]和 Fenz等[56]研究了双凹摩擦摆两个凹表面曲率半径和摩擦系数不相等的情况.Kim等[7]研究了强震作用下桥梁采用三线性模型双凹摩擦摆较之于双线性模型双凹摩擦摆的优越性，认为三线性双凹摩擦摆比双线性双凹摩擦摆的桥墩基底剪力降低15%∼40%.

本文对采用双凹摩擦摆中间隔震的烟风道结构的地震响应进行研究.由于隔震结构为非经典阻尼结构体系，采用时程分析方法.首先建立了简化的三线性双凹摩擦摆烟风道隔震体系的三自由度地震响应分析模型，根据理论模型编写了程序，并用实体有限元建模分析，验证理论模型的正确性.然后，利用理论模型研究了不同场地、不同强度地震激励下双凹摩擦摆、道体反力、支架剪力的地震响应.

1 双凹摩擦摆滞回模型

双凹摩擦摆(double concave friction pendulum,DCFP)可视为两个单摩擦摆串联而成.第i个单摩擦摆的恢复力为[6]

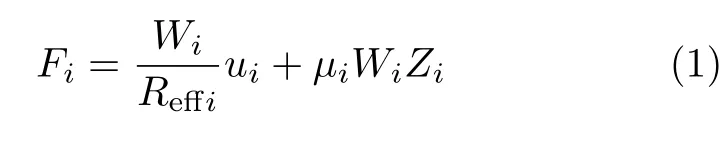
式中，Wi为第i单摩擦摆承受的重量，ui为滑块相对于第i单摩擦摆滑移面的水平位移，µi为第i单摩擦摆滑移面摩擦系数，Zi为滞回变量，Reffi为第i单摩擦摆滑移面等效半径.

当滑块铰接点位于滑移面内侧时，等效半径为[6]

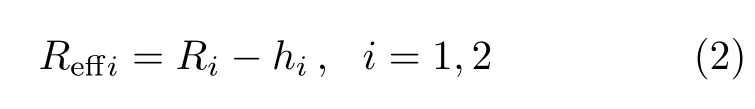
式中，Ri为柱面滑移面i半径，hi为铰接点至滑移面i的径向距离.

滞回变量Zi的控制方程为[6]

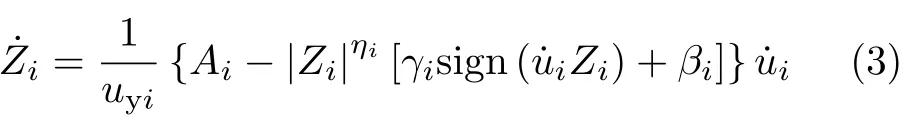
式中，uyi为屈服位移，˙ui为滑块相对于第i单摩擦摆滑移面的速度;Ai,γi,βi和ηi为控制滞回环形状的无量纲参数.

摩擦系数µi和速率有关.摩擦系数随速度的变化关系如下[8]

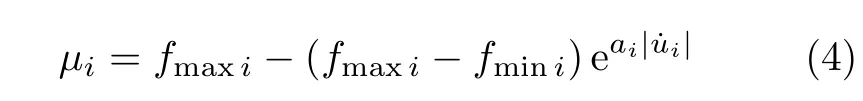
式中，fmaxi和fmini分别为与滑块较大速度和较小速度相对应的滑动摩擦系数，ai为控制两种摩擦系数转换的参数.

典型的双凹摩擦摆隔震支座三线性滞回模型如图1所示[9].当双凹摩擦摆上下摩擦系数相等时，地震作用下，铰接滑块会与上、下滑动面同时产生相对运动.滞回模型为双线性[4].若双凹摩擦摆上下摩擦系数不等，滑块在摩擦系数较小的滑动面首先发生相对滑动，而在另一个滑动面则相对静止，此阶段隔震支座的刚度为W1/Reff1.当位移u1增大至一个限值u∗时，滑块在摩擦系数较大的滑动面也开始滑动，此阶段隔震支座的刚度减小为W1/(Reff1+Reff2).

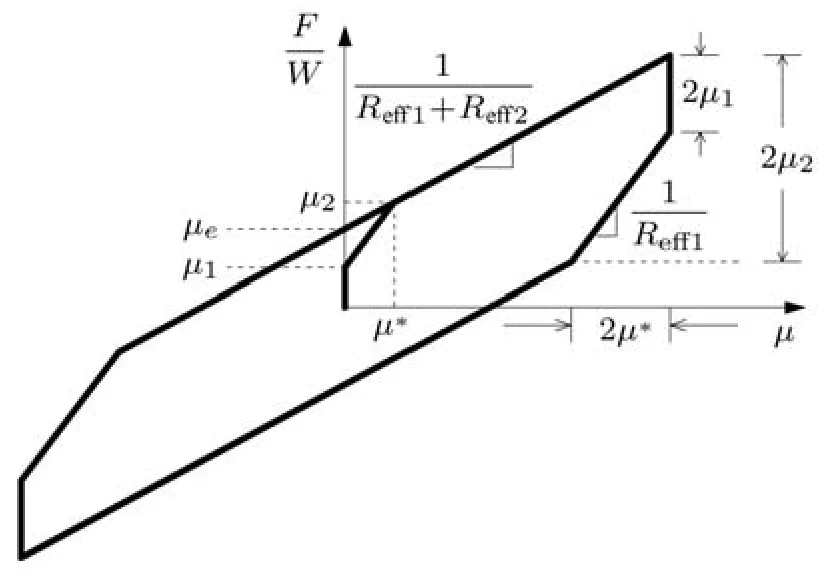
图1 双凹摩擦摆隔震支座三线性滞回模型,F为总的摩擦摆恢复力

2 双凹摩擦摆隔震烟风道结构体系地震响应模型

将隔震支座设于道体和支架之间,烟风道简化为三质点模型，见图2.在横向水平地震作用下，道体的地震响应有明显的降低，可认为道体为刚体运动，并简化为单质点md,支架结构质量集中于单质点ms,双凹摩擦摆采用三线性滞回模型.为了分别研究两个单摆的特性，两个串联单摆FPS1和FPS2采用一个很小的滑块质量为mb连接.

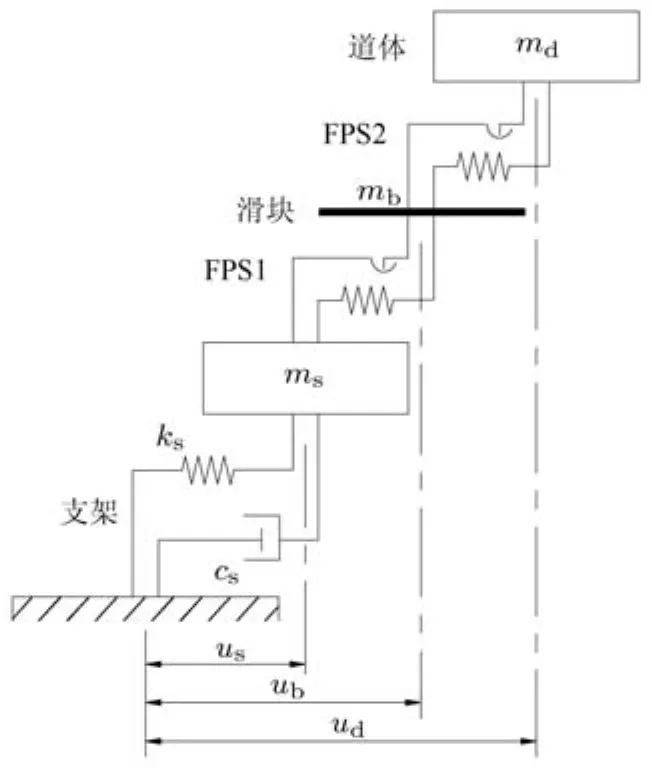
图2 三自由度双凹摩擦摆隔震烟风道模型

图 2中，ks和 cs分别为支架的刚度和原结构(支架+道体)黏滞阻尼系数，ud,us,ub分别为道体质点、支架质心和滑块质点相对地面的侧向位移.

该体系在地震作用下的运动方程可表达为

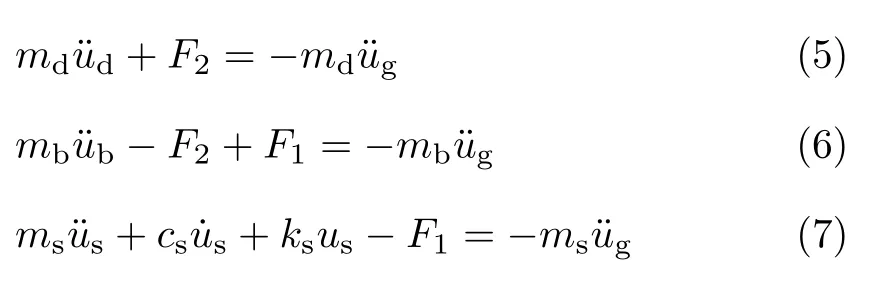
式中，Fi为第i个单摩擦摆的恢复力，见式(1)，其中，u1=ub−us，u2=ud−ub;¨ug为水平地面运动加速度.因抗震规范规定只有部分活载荷产生惯性质量，又因支座的自重比道体作用在支座上的重量小得多，故取W1=κmdg≈W2,κ为重力载荷代表值与道体质量的比值.

式 (6)和式(7)给出的运动方程可以简化成一阶状态空间的形式

式中，状态矢量X 为

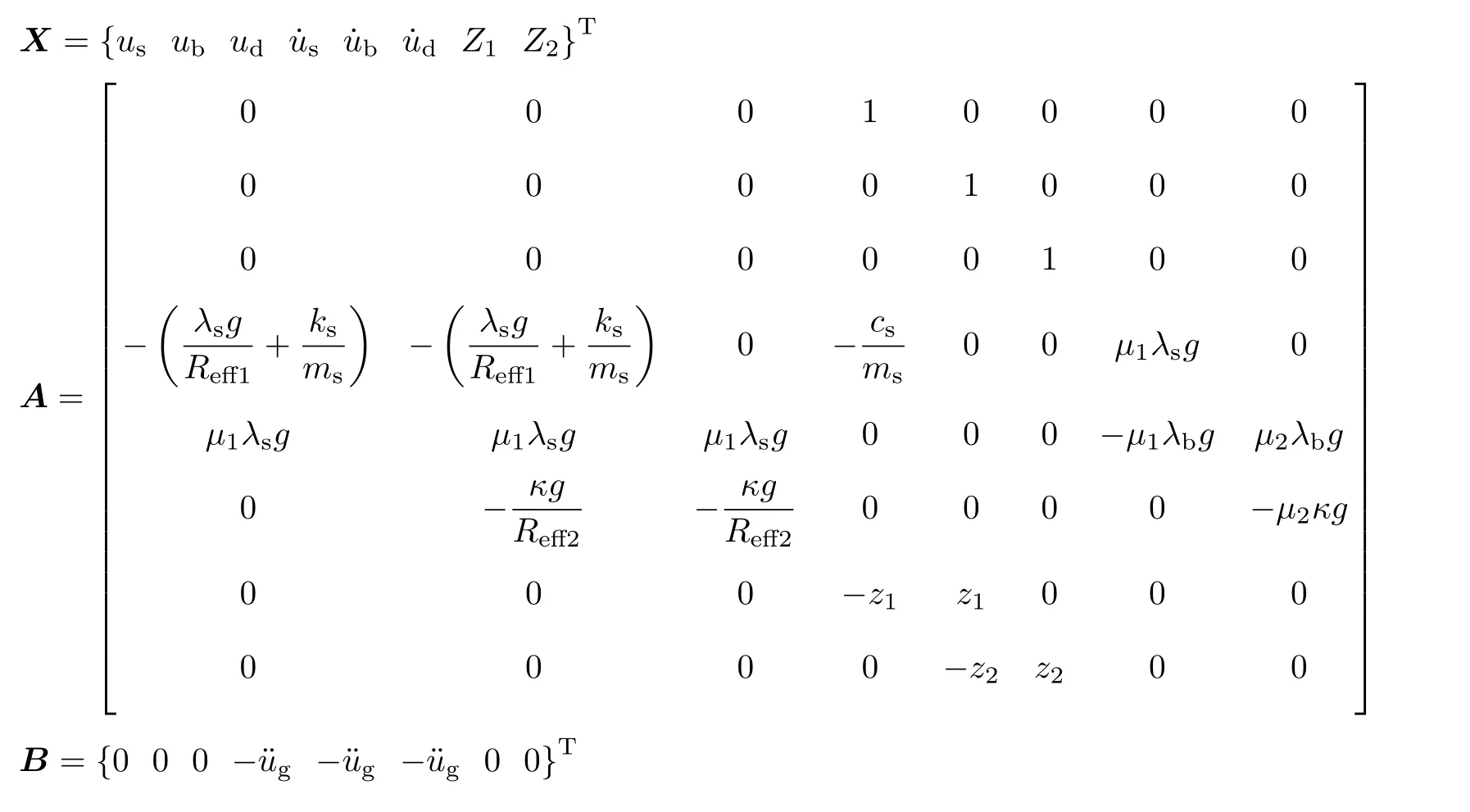
矩阵A中

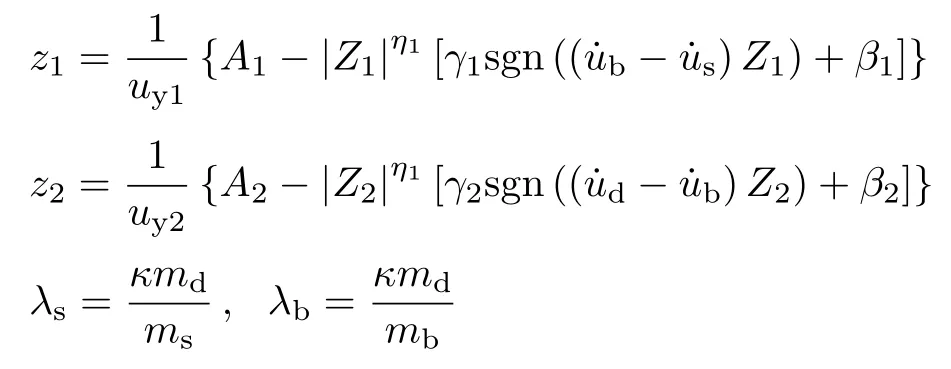
定义道体水平反力(即FPS2恢复力)、FPS1恢复力与道体质量的比值分别为

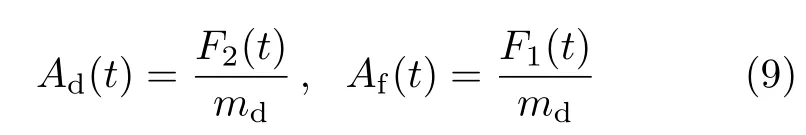
Ad(t)为道体质点的绝对加速度.

定义支架底部剪力与结构总质量的比值为

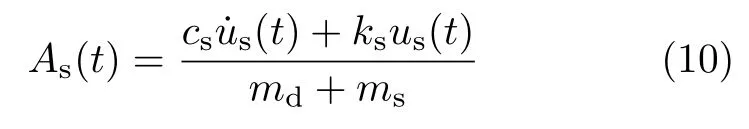
式中

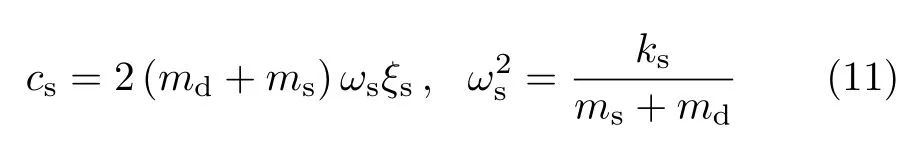
其中，ξs为结构的阻尼比，ωs为结构的固有自由振动频率.

由式 (8)可知，系数矩阵 A 只取决于 λs=以及上、下滑面等效半径.当等效半径一定，整个结构地震响应取决于道体和支架的质量比、支架的刚度和质量比.

3 模型验证

采用Matlab软件编程，对上述三自由度隔震体系动力模型进行非线性时程分析，式(8)的8个一阶线性常微分方程采用ode15s求解器求解.由于烟风道结构、质量分布均匀，结构地震响应取决于道体和支架的质量比、支架的刚度和质量比，验证模型选取一个支架及其上部的双凹摩擦摆、载荷与惯性质量.为了验证理论模型与计算程序的正确性，用有限元软件Abaqus建立与Matlab程序参数相同的三维实体模型，见图3.双凹摩擦摆采用采用8节点六面体线性减缩积分单元(C3D8R)，支架采用梁单元.计算时，假设支架底固定，支架保持在弹性范围内，非线性仅限于支座.非线性时程分析采用Newmark直接积分，时间步长为0.005s.

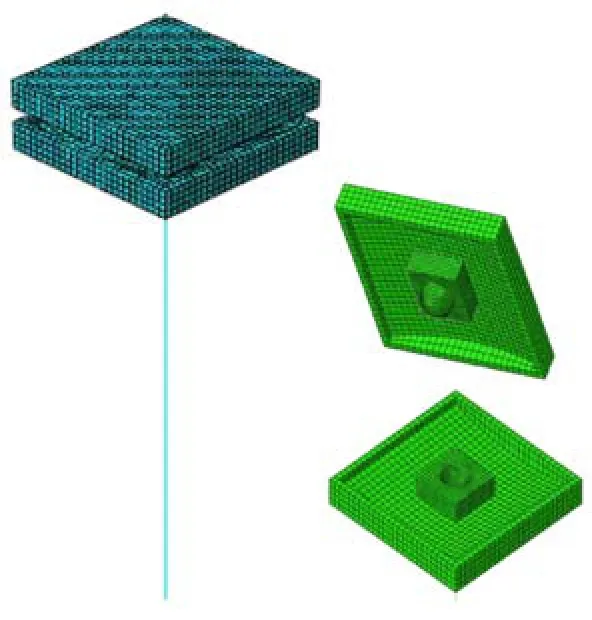
图3 双凹摩擦摆隔震烟风道结构有限元模型

双凹摩擦摆上滑面等效半径Reff2=470mm，滑动摩擦系数fmax=0.03,fmin=0.01；下滑移面等效半径Reff1=460mm，滑动摩擦系数fmax=0.12,fmin=0.1.Ai=1，γi=βi=0.5.图 4为拟静力实验得到的该参数双凹摩擦摆的三线性滞回曲线.

双凹摩擦摆惯性质量 mb=0.686kN/g. 烟风道支架刚度 ks=6.84kN/mm，支架惯性质量ms=4.96kN/g. 道体恒载与活载在支座上产生的重量 W=135kN.取 κ=1.35，则惯性质量md=100kN/g. 结构阻尼为瑞雷阻尼，其质量比例系数和刚度比例系数取值对应的结构周期为0.1s∼1s时,模态阻尼比为0.02.

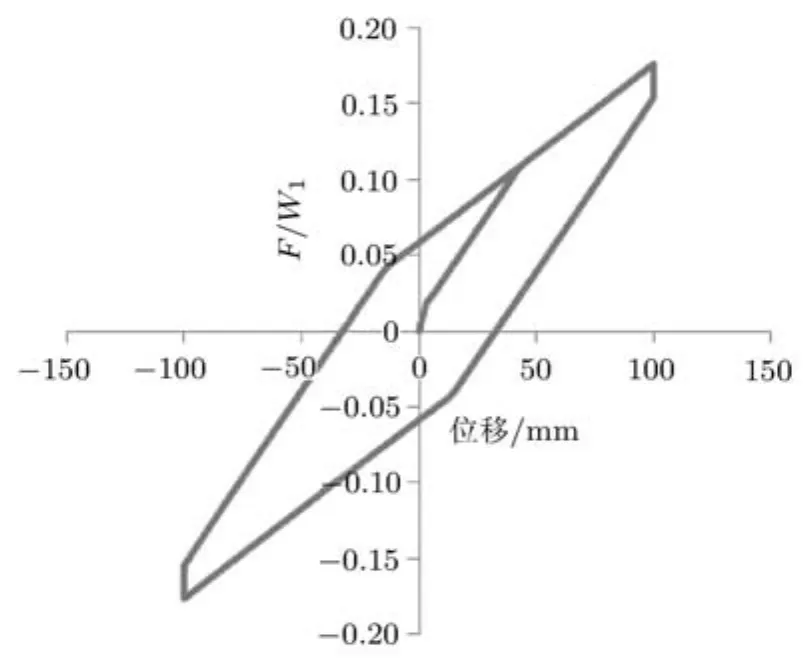
图4 双凹摩擦摆滞回曲线

地震激励分别取(1)正弦简谐激励2种，周期为5s，幅值分别为250gal和150gal，1gal=1cm/s2,持续时间 30s和 (2)6条实际地震波.地震波为：① II类场地 EL Centro波 (简称 EL波)南北方向分量，地面运动峰值加速度 (Peak Ground Acceleration)PGA=341.7gal;② III类场地 CPCTOPANGA波 (以下简称 CPC波)S16W 分量，持时 55.58s，步长 0.02s，记录的 PGA=380.98gal;③ Kobe波，PGA=344.7gal，持时 40.9000s，步长 0.01s；④ Northridge波，PGA=568.3gal，持时 39.9s，步长 0.01s；⑤ Loma Prieta波 (以下简称Loma)，PGA=367.4gal，持时 39.9s，步长 0.01s；⑥Trinidad波，PGA=193.6gal，持时 21.4s，步长0.01s.

考虑罕遇地震，EL波、CPC波的PGA分别按抗震规范调整为310gal(7度)、510gal(8度)，分别代表强震和超强震情况.由于非线性隔震结构的地震响应受地震动输入选择的影响较大，为了使计算结果之间有可比性，以EL波、CPC波的反应谱为目标谱，将 Kobe波、Loma Prieta波调整成与 EL波具有基本相同的反应谱，共2组；Northridge波、Trinidad波调整成与 CPC波具有基本相同的反应谱，共2组.调整后地震波PGA及分组见表1.

图5为谐振地面运动PGA=150gal、EL Centro波PGA=510gal，有限元与理论模型的道体反力与位移关系Ad∼ud对比.可以发现，本文提出的简化模型与有限元计算结果非常接近，可用于双凹摩擦摆隔震烟风道结构地震响应分析，而比三维实体有限元模型更简单，节约大量计算时间.

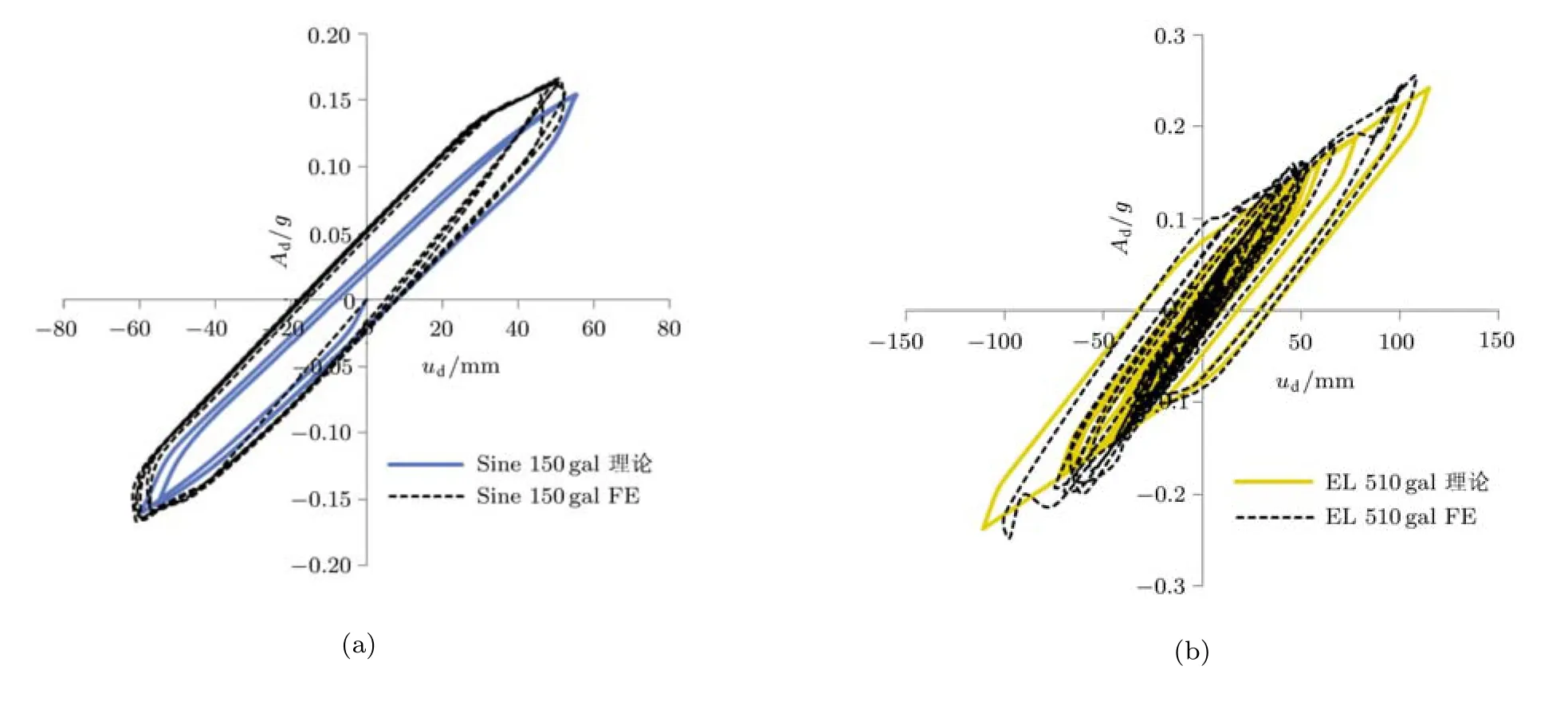
图5 有限元与理论模型道体反力Ad与位移ud关系对比

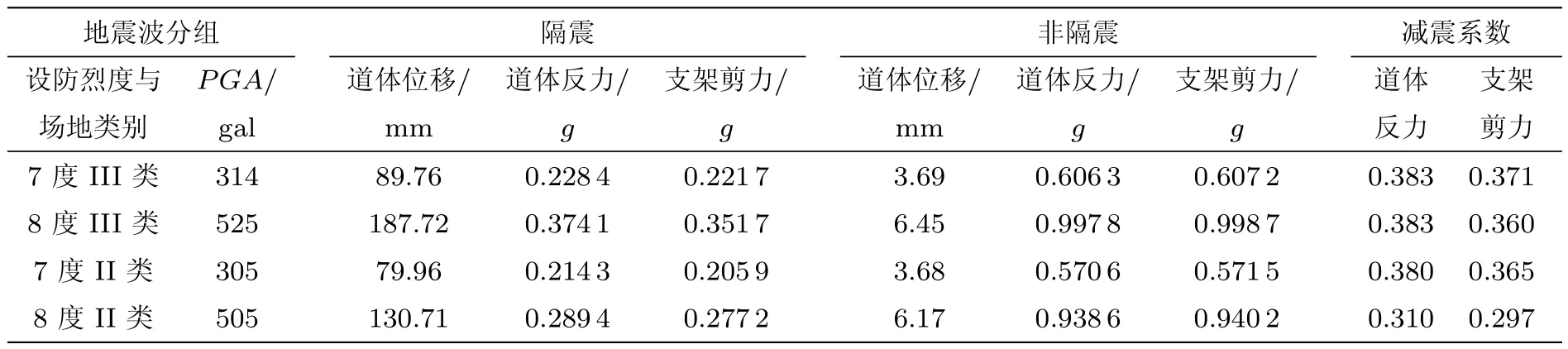
表1 隔震、非隔震道体、支架最大时程响应比较

图6为简化模型在谐振、EL Centro波、CPC波激励下，双凹摩擦摆的Ad--(ud−us)、上摆FPS2的Ad--(ud−ub)、下摆FPS1的Af--(ub−us)的滞回曲线.双凹摩擦摆滞回曲线表现出明显的三线性特征.由于上滑移面摩擦系数较小，双凹摩擦摆位移主要是由FPS2(即滑块在上滑移面的滑移)引起的.同一场地条件下，随着PGA的增加，FPS1的位移越接近FPS2，即滑块在上下两个滑移面的滑移量越接近.

图6 不同地震激励下双凹摩擦摆、上摆FPS2、下摆FPS1力与位移关系

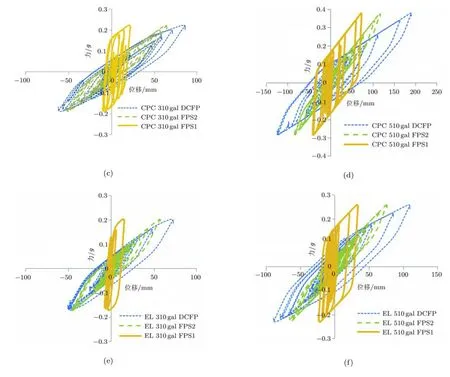
图6 不同地震激励下双凹摩擦摆、上摆FPS2、下摆FPS1力与位移关系(续)

4 地震作用下双凹摩擦摆隔震烟风道结构最大时程响应

采用简化模型，选取整个烟风道为研究对象.得到4组12种地震激励下，隔震与非隔震结构的道体水平位移、道体水平反力和支架剪力时程响应.

EL波(PGA=510gal)激励下，非隔震结构和隔震结构道体反力时程对比如图7所示.隔震结构道体反力始终小于非隔震结构，且双凹摩擦摆隔震效果非常显著.

各时程响应以及水平向减震系数 (隔震结构与非隔震结构剪力或反力之比)绝对最大值见表1.表中还列出了每组地震波的3个时程响应最大值的均值.

目标谱PGA=310gal情况下，III类场地组地震激励得到的道体反力与支架剪力的平均减震系数分别为0.383和0.371，而II类场地组地震激励得到的道体反力与支架剪力的减震系数分别为0.380和0.365.表明强震情况下，II类场地的双凹摩擦摆隔震效果略优于III类场地.

目标谱PGA=510gal情况下，III类场地组地震激励得到的道体反力与支架剪力的减震系数分别为0.383和0.360，II类场地组地震激励得到的道体反力与支架剪力的减震系数分别为 0.310和 0.297.表明超强震情况下，场地越硬，DCFP隔震效果越显著.

目标谱 PGA 由 310gal增加到 510gal，III类场地地震激励产生的道体反力和支架剪力减震系数均值变化很小，而II类场地地震激励得到的道体反力和支架剪力减震系数均值减小较多.因此，无论是道体还是支架剪力，II类场地隔震效果要优于III类场地，而且PGA越高，隔震效果越好.

各组输入的 3条地震波虽然具有相同的反应谱，但时程响应结果差别较大，特别是位移响应.隔震结构道体的水平位移明显大于非隔震结构，这主要是双凹摩擦摆滑块沿两个滑移面发生相对滑动引起的.对于隔震结构，目标谱PGA相同条件下，III类场地组地震激励引起的道体位移远大于II类场地组地震激励引起的道体位移.

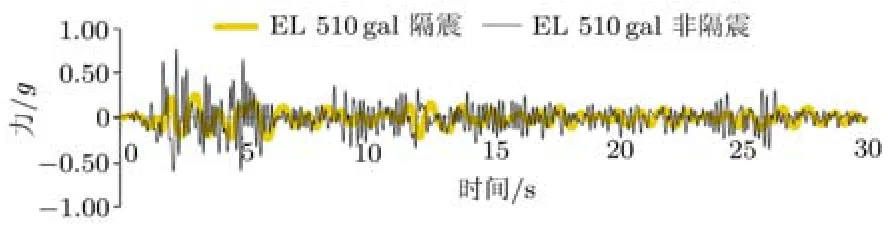
图7 EL Centro波(PGA=510gal)道体反力时程

5 结论

摩擦摆隔震支座用于烟风道，可以同时具有减少摩擦力和隔震功能，允许道体在支座上自由转动.本文对烟风道采用双凹摩擦摆中间隔震的烟风道体系的地震响应进行了研究.建立了简化的三线性双凹摩擦摆隔震体系的三自由度结构地震响应分析模型，推导了一阶状态空间微分运动方程.该模型的分析结果与有限元程序Abaqus建立的实体模型分析结果非常接近，证明该简化模型是正确的.

利用所建立的简化模型研究了不同场地类别、不同地震激励作用下双凹摩擦摆隔震效果.研究表明：(1)同一场地条件下，当PGA较小时，双凹摩擦摆滑块在摩擦系数较小的面滑移量远大于在摩擦系数较大的滑移面的滑移量.随着PGA的提高，滑块在两个滑移面的滑移量越接近.(2)场地越坚硬，双凹摩擦摆隔震效果越好，道体位移越小.对于II类场地，PGA越高，减震系数越小.(3)双凹摩擦摆隔震结构的非线性地震响应最大值，不仅与地震运动加速度幅值、频谱成分有关，还与地震动的全过程关系密切.虽然每一组3条地震波具有相同的反应谱，但其非线性时程响应最大值差别很大.

1 Hyakuda T，Saito K，Matsushita T，et al．The structural design and earthquake observation of a seismic isolation building using Friction Pendulum system．7th WCSI，Assisi，Italy，2001

2 Buckle IG,Constantinou M,Dicleli M,et al. Seismic isolation of highway bridges. Special Report MCEER-06-SP07,Multidisciplinary Center Earthquake Engineering Research,University at Buffalo,NY,2006

3 Tsai CS,Chiang TC,Chen BJ.Experimental evaluation of piecewise exact solution for predicting seismic sesponses of spherical sliding type isolated structures.Earthquake Engineering and Structural Dynamics,2005,34(9):1027-1046

4 Constantinou MC.Friction pendulum double concave bearing.NEES Report,http://nees.buffalo.edu/dec304/FPDC%20Report-DEMO.pdf,2004

5 Fenz DM,Constantinou MC．Mechanical behavior of multispherical sliding bearings．Technical Report MCEER-08-0007,University of Buffalo,2008

6 Fenz DM,Constantinou MC.Behaviour of the double concave friction pendulum bearing.Earthquake Engineering and Structural Dynamics,2006,35(11):1403-1424

7 Kim YS,Yun CB.Seismic response characteristics of bridges using double concave friction pendulum bearings with tri-linear behavior. Engineering Structures,2007,29(11):3082-3093

8 Constantinou MC,Whittaker AS,Fenz DM,et al.Seismic isolation of bridges.Version 2,Report to Sponsor,California Department of Transportation,2007

9 邓雪松，龚健，周云.双凹摩擦摆隔震支座理论分析与数值模拟研究.广州大学学报(自然科学版),2010,9(4):71-77

SEISMIC RESPONSE OF ISOLATED GAS DUCT USING DCFP BEARING1)

FENG RuoyuCHEN Ying2)WANG HuiBAI Jie
(School of Civil Engineering,Shandong University,Jinan 250061,China)

The duct slide bearing plates are used to reduce the friction force as the duct expands and contracts under temperature variations,but can not be used for seismic isolation without the re-centering capability.In this paper,a double concave friction pendulum system(DCFP)with tri-linear hysteretic behavior is adopted for the gas duct both for thermal displacement and seismic isolation.The seismically isolated duct is modeled as a three-degree-of-freedom system in the transverse direction.The first order state space formulation of the equations of motion is derived,and the theoretical analysis is verified by the finite element analysis.Then the effects of the DCFP on a gas duct and its hysteretic behavior are investigated under various earthquake excitations.Comparing with a duct without the seismic isolation，the reaction force on the DCFP and the shear force on the pier are both greatly reduced.

seismic isolation,duct,double concave friction pendulum,tri-linear hysteretic model

O39

A

10.6052/1000-0879-16-418

2016-12-21收到第1稿，2017-04-26收到修改稿.

1)国家自然科学基金(41172267)、国家科技支撑计划(2015BAB07B05)和2016年国家级大学生创新创业训练计划(201610422087)资助.

2)陈瑛，博士，副教授，主要从事结构抗震、隔震与复合材料力学等领域教学与科研工作.E-mail:chenying@sdu.edu.cn

冯若愚,陈瑛,王辉等.双凹摩擦摆隔震烟风道结构地震响应.力学与实践,2017,39(5):472-478

Feng Ruoyu,Chen Ying,Wang Hui,et al.Seismic response of isolated gas duct using DCFP bearing.Mechanics in Engineering,2017,39(5):472-478

(责任编辑:周冬冬)