利用上游槽道对角区马蹄涡的控制
2017-11-22李健张华吴星钢
李健, 张华, 吴星钢
北京航空航天大学 航空科学与工程学院, 北京 100083
利用上游槽道对角区马蹄涡的控制
李健, 张华*, 吴星钢
北京航空航天大学 航空科学与工程学院, 北京 100083
在平板上放置圆柱形成角区流动,利用布置在圆柱上游平板上的二维和三维槽道来控制或削弱角区马蹄涡,采用风洞试验和数值模拟开展研究。结果表明,二维和三维槽道均能推迟边界层的分离,使圆柱根部马蹄涡的强度减弱、尺度减小;同时槽道上游压力和逆压梯度均有所下降,槽道下游压力显著升高而逆压梯度总体降低。二维槽道对马蹄涡强度的削弱为61.15%~66.51%,而三维槽道对其削弱为66.65%~80.93%。讨论了三维槽道参数(包括槽道宽度、深度以及其中心线与圆柱中心距离)对控制效果的影响。槽道与圆柱的距离在对马蹄涡的控制中起主导作用。槽道控制的机理是,由于槽道的抽吸效应使得其上游靠近壁面的边界层中涡量较高的流体被卷吸入槽道形成槽道涡,槽道涡由三维槽道输运到下游。同时,随着槽道与圆柱的距离减小,更多的边界层流体流入槽道内。正是上述“槽道效应”使得槽道下游的逆压梯度降低,马蹄涡强度减弱,分离区范围减小。
角区流动; 马蹄涡; 流动控制; 上游槽道; PIV试验
边界层流体遇到壁面凸起的障碍物后,通常会在障碍物产生的逆压梯度作用下发生三维流动分离并形成马蹄涡结构,这种流动称为角区流动。角区流动形成的马蹄涡使障碍物前缘根部流场受到非定常扰动,从而产生噪声、振动等问题[1-3]。马蹄涡将边界层外部的自由流体卷入到角区内,导致角区热交换率大大改变[4-5],同时增加了局部表面剪切应力[6]。马蹄涡能向下游延伸很长的距离,给下游流场造成扰动[7-8]。
正是由于上述角区流动中马蹄涡带来的诸多影响,国内外学者对马蹄涡进行了大量的研究。Seal等[9]通过试验和数值计算发现马蹄涡系是由多对反向旋转的涡组成的,这些涡系在高雷诺数下表现出周期性的特点。Khan和Ahmed[10]通过试验研究了翼型-平板角区涡系随雷诺数增大的演化情况,结果表明随着雷诺数增大,涡系依次经历定常、振荡融合和脱落破裂3个阶段。在定常阶段,涡系随雷诺数的增加依次由单一涡系向三涡系演化,整个涡系保持稳定。Greco[11]第一次全面地将角区马蹄涡流动行为分为:定常、振荡、合并、脱落、转捩5种情况,上述5种状态基本可以概括马蹄涡系的所有运动特征。
为了减小马蹄涡带来的不利影响,各种控制方法得到大量研究。Philips等[12]使用一个抽吸狭缝进行控制,发现大尺度的马蹄涡消失。Johnson等[13]使用角区上游吹吸孔进行控制,发现随着吹气速率的增加,马蹄涡的形成被推迟。徐向南等[14]通过利用DBD(Dielectric Barrier Discharges)涡流发生器诱导与马蹄涡环绕方向相反的涡,实现对马蹄涡的控制。Devenport等[15]研究了放置在叶片底部周围的固定半径凹形填角的控制效果,结果表明凹形填角推迟了叶片前缘流动分离。他们在随后的研究中[16]发现,前缘凸脊能够减小角区上游的逆压梯度并推迟边界层分离。Nelson等[17]研究了肋状表面对于平板-圆柱形成的角区的控制效果,研究发现平板表面附近的湍流雷诺应力有所减小。Kairouz和Rahai[18]研究斜杆对马蹄涡的控制效果,结果表明在斜杆控制下马蹄涡的强度减弱,同时马蹄涡被控制在远离角区附近的区域内。
槽道控制作为一种被动控制,由于能够对角区流动产生的马蹄涡有很好的控制效果,因而也得到了国内外学者的关注。Horsten和Veldhuis[19]研究了机身与插入其的支撑装置间的槽道对该连接区域流动的影响,试验和数值模拟结果都表明槽道减小了支撑装置与机身连接处上游的逆压梯度,从而阻止了气流分离。Kang等[20]利用试验手段对二维矩形截面槽道层流角区控制进行了研究。试验结果表明槽道能够降低其上游的逆压梯度,推迟流动分离,同时马蹄涡的强度降低。Zaw Zaw[21]利用数值模拟对布置在平板-圆柱角区上游的不同尺寸的二维矩形截面槽道进行了研究,发现槽道越深越宽对马蹄涡强度的控制越明显,同时槽道放置越靠近圆柱前缘区域,其控制效果越明显。
本文利用试验和数值模拟研究了布置在角区上游的二维和三维矩形槽道对马蹄涡的控制效果,由于三维槽道具有比二维槽道更好的对边界层涡量的输运能力从而对马蹄涡的控制效果更好,本文进一步研究了三维矩形槽道参数,即槽道深度L、宽度W以及槽道中心线距离圆柱中心的距离C对于马蹄涡控制的影响。
1 试验设备与技术
试验在北京航空航天大学D-1风洞中进行。D-1风洞是回流式开口低速风洞,最大风速为50 m/s。试验风速选择为25 m/s,来流湍流度小于0.5%。试验段截面为椭圆形,入口截面尺寸为1.02 m×0.75 m,出口截面为1.07 m×0.81 m,试验段长1.45 m。试验采用在平板上放置圆柱形成的角区模型,圆柱直径D=100 mm,高H=250 mm,圆柱前缘距平板前缘750 mm。试验中使用的二维、三维槽道截面均为矩形。二维槽道的中心线为直线且垂直于来流放置于圆柱前缘,槽道横跨整个平板。三维槽道中心线几何形状为角区流动无控制情况下分离区最外侧分离线的轮廓,槽道对称放置于圆柱前缘。三维槽道参数分别为:C/D=0.75,0.95,1.15,1.35,1.55,1.75;L/D=0.1,0.2,0.4;W/D=0.2,0.3,0.4。本文采用油流显示、测压以及二维粒子图像测速(PIV)试验手段。油流根据具体流动情况由钛白粉、煤油和硅油按一定的比例混合而成。角区流动壁面静压的测量采用美国PSI压力扫描阀。PIV系统光源为双腔Nd:Yag激光器,跨帧时间间隔为Δt=200~600 ns,激光器功率为200 Mj/脉冲,CCD相机的分辨率为2 448×2 050 像素,数据采集频率为5 Hz。PIV试验所用粒子由舞台发烟机产生,属于固体粒子,直径小于1 μm。PIV试验观测窗口尺寸为74 mm×24 mm。
2 数值方法及验证
本文采用商业CFD软件FLUENT 14.5[22]的分离求解器求解三维非定常不可压雷诺时均方程组得到流场结构。选取Spalart-Allmaras湍流模型,求解过程采用SIMPLE耦合算法,Navier-Stokes方程组空间离散项均采用二阶迎风格式,时间项采用二阶隐式格式。计算域的选取与试验设置类似,未布置槽道的计算域如图1所示。
入口距平板前缘100 mm,定义为速度入口,速度U∞为25 m/s,来流湍流黏度比率为1。出口设为压力出口,静压表压为0,回流湍流黏度比率为1。计算域两侧、顶部以及入口距平板前缘段均设为对称面边界条件,其他壁面设为无滑移壁面。网格采用专业网格生成软件ICEM生成结构化网格,对于不同工况网格数略有差异,但总数在400万节点左右,图2为二维和三维槽道局部网格。
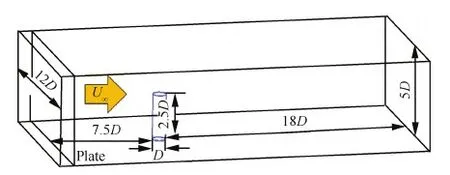
图1 平板-圆柱角区计算域的尺寸Fig.1 Computational domain size of flat plate-cylinder junction
为验证上述数值方法的可靠性,将不施加控制情况下平板-圆柱角区流动试验数据与计算结果进行比较。图3为数值计算得到的时均壁面摩擦力线与油流试验结果的对比,可以发现数值计算所得到的最外侧分离线S1和二次分离线S2与试验结果基本一致。图3中Lfront/D和Lleft/D分别表示S1与垂直轴线和水平轴线交点距圆柱中心的距离。图4为计算域对称面处流场的计算结果时均值与PIV试验时均值的对比,计算得到的对称面涡系结构以及主涡涡心的位置和高度与试验结果吻合很好。
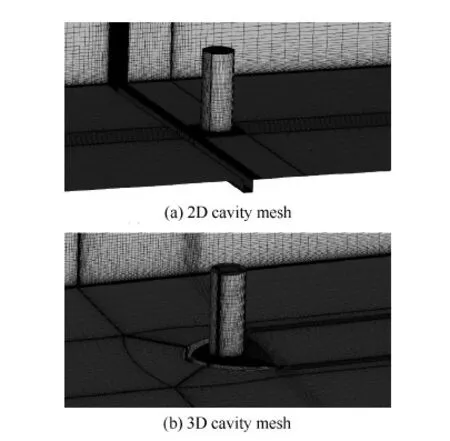
图2 二维和三维槽道计算网格Fig.2 2D and 3D cavity computation meshes
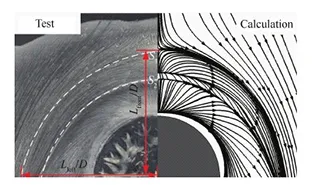
图3 时均壁面摩擦力线Fig.3 Time-averaged skin friction lines on wall

图4 流场对称面处流线时均结果Fig.4 Time-averaged results of streamlines in symmetry of stream field
3 结果和讨论
3.1 壁面摩擦力线及对称面马蹄涡变化
本文对试验和计算的讨论均采用时均结果。图5是无槽道控制、二维和三维槽道控制工况下表面摩擦力线的试验结果,其中二维和三维槽道均选取深度为L/D=0.4、宽度W/D=0.3、槽道中心线距离圆柱中心C/D=1.15的矩形截面槽道。图6是上述3种工况下分离线S1与圆柱中心左侧的距离Lleft/D以及其与圆柱中心前侧的距离Lfront/D。结果均表明二维和三维槽道都能使分离线前侧和两侧向圆柱靠近,从而使得流动分离范围减小,同时可以看出,三维槽道控制下的分离范围要小于二维槽道控制下的分离范围。
图7依次给出了无控制、二维和三维槽道控制下流场对称面流线图和涡量云图。试验和计算结果都表明,在槽道控制下马蹄涡向圆柱前缘和壁面靠近,马蹄涡尺度减小。同时对比二维和三维槽道控制效果可以看出,在三维槽道控制下马蹄涡更加靠近圆柱前缘和壁面。

图5 壁面摩擦力线试验结果Fig.5 Mean skin friction lines on wall results of test
图8给出了试验和计算得到的流场对称面处马蹄涡环量,结果表明,二维槽道使马蹄涡的强度降低了61.15%~66.51%,而三维槽道使其降低了66.65%~80.93%。三维槽道控制效果强于二维槽道。
图9是改变三维槽道与圆柱的距离C/D、宽度W/D以及深度L/D得到的壁面分离线S1与圆柱中心左侧距离Lleft/D和前侧距离Lfront/D。可以看出,随着槽道与圆柱距离的减小,分离范围在不断减小。同时,随着槽道深度和宽度的增加,分离范围不断减小。由图9还可以看出,槽道距离参数对于分离范围的减小影响较为显著。
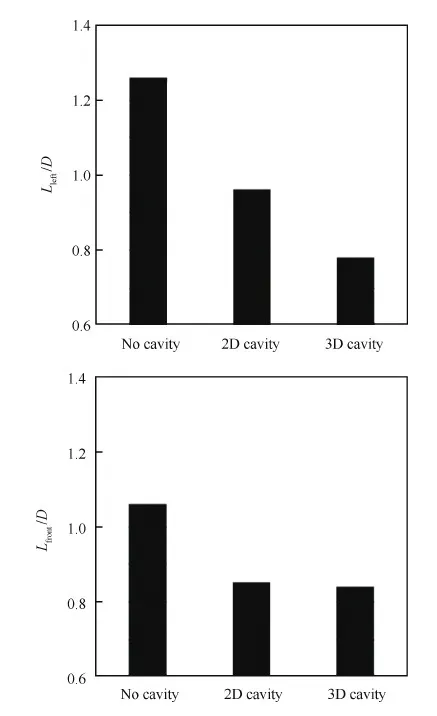
图6 无控制工况、二维槽道和三维槽道控制下分离范围对比Fig.6 Comparison of separation region with no cavity control, 2D and 3D cavity control
3.2 流场对称面壁面压力
图10是无控制、二维和三维槽道控制下对称面处壁面测压试验结果,Cp为压力系数。结果表明,槽道上游压力和逆压梯度较无控制工况都降低了。槽道下游压力显著上升,靠近圆柱前缘压力基本保持不变。槽道下游逆压梯度总体上较无控制工况有所降低,同时马蹄涡诱导的局部低压区变得更为平坦且向圆柱前缘靠近。槽道内部的低压区是由槽道涡诱导的。由图10还可以看出,三维槽道对上、下游逆压梯度的降低要强于二维槽道,同时三维槽道涡诱导的低压区压力要小于二维槽道涡所诱导的。来流中靠近壁面的涡量较高、动量较低的流体由三维槽道输运到角区下游,从而降低了上游压力和逆压梯度,减小了流动分离范围。而槽道下游的流体主要来自上游远离壁面的边界层中涡量较低、动量较高的流体,在靠近圆柱前缘附近,流体动能全部转化为压力势能,压力升高。二维槽道控制能力弱于三维槽道是由于二维槽道无通道将槽道内部流体输运到圆柱下游,从而造成内部涡量向两端堆积,最终从槽道两端溢出,槽道输运能力不足。

图7 流场对称面流线和涡量云图时均结果Fig.7 Time-averaged results of streamlines and vorticity in symmetry of stream field

图8 流场对称面马蹄涡环量变化Fig.8 Circular of horseshoe vortex in symmetry of stream field
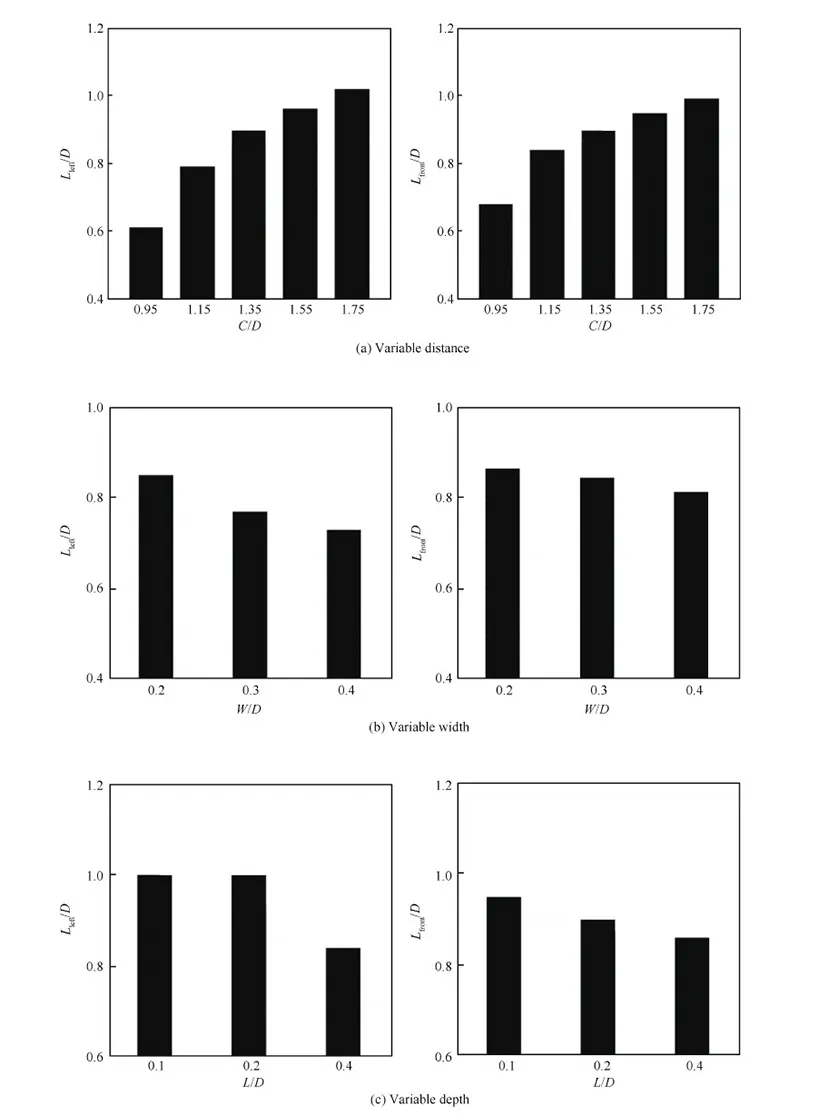
图9 三维槽道参数对流动分离的影响Fig.9 Effect of 3D cavity parameters on flow separation region
图11分别是对称面处壁面压力随槽道距离、宽度和深度改变而得到的槽道下游压力分布。结果表明,随着槽道距离减小,下游压力不断上升而逆压梯度不断下降。同时,马蹄涡强度不断降低且向圆柱前缘靠近。增加槽道宽度和深度也有相同的结论,但对逆压梯度和马蹄涡强度的降低程度没有距离参数对其降低的显著。
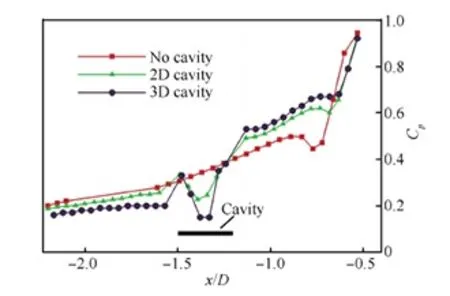
图10 无控制、二维和三维槽道控制下流场对称面处壁面压力系数时均分布试验结果(L/D=0.4,W/D=0.3,C/D=1.35)Fig.10 Test results of time-averaged surface pressure coefficient distribution in symmetry of stream field with no control, 2D cavity and 3D cavity control (L/D=0.4,W/D=0.3,C/D=1.35)
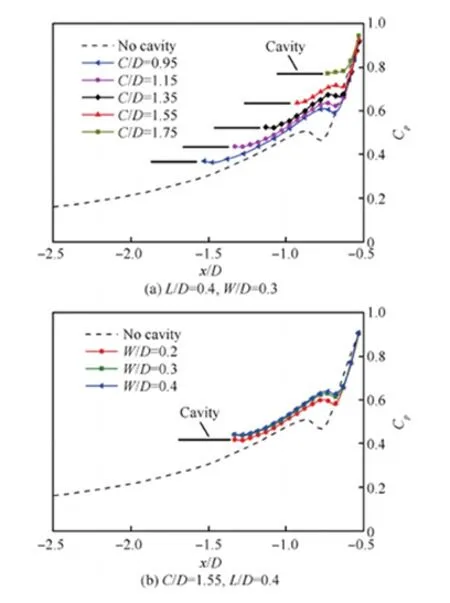
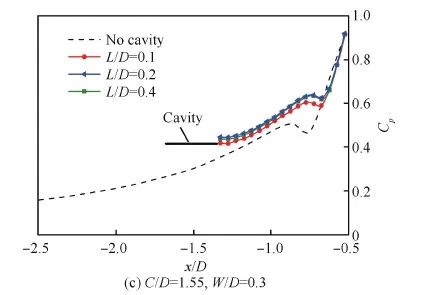
图11 槽道距离C、宽度W和深度L对槽道下游对称面压力分布影响Fig.11 Effect of cavity parameter distance C, width W and depth L on distribution of cavity downstream symmetry pressure
3.3 槽道控制机理
图12是固定槽道深度L/D=0.4,宽度W/D=0.3,改变槽道距离C得到的对称面流线和涡量的试验结果,以及利用λ2法则提取的上述试验对应的数值模拟结果的空间涡结构。图13(a)和图13(b)分别是数值模拟得到的流场对称面处马蹄涡以及槽道涡的环量,I1/Ino和I2/Ino分别表示槽道控制下马蹄涡环量和槽道涡环量与无控制工况下马蹄涡环量的比值。可见当槽道和圆柱距离不断减小,马蹄涡不断向圆柱和壁面靠近,马蹄涡尺度减小,强度减弱,当距离减小到小于C/D=0.75时,马蹄涡几乎消失。同时随着槽道与圆柱距离不断减小,经槽道输运的涡量不断增多。
图14为三维槽道在不同距离参数下流场对称面流线,图中红色流线将来流边界层分为两层。其中来流边界层中靠近壁面的涡量较高、动量较低的流体被卷吸入槽道,形成槽道涡,并由槽道的两侧通道输运到圆柱下游。而远离壁面的涡量较低、动量较高的流体直接流向槽道下游,并在圆柱根部附近形成马蹄涡。由图14还可以看出,随着槽道向圆柱靠近,更多的边界层流体流入槽道内,从而使得流向槽道下游的边界层变薄。正是由于槽道具有以上“槽道效应”,才使得槽道下游马蹄涡强度减弱,而壁面分离范围减小,同时马蹄涡的非定常特性被抑制。计算结果还表明,当槽道尺寸过小时,槽道无法输运走足够的涡量,使得流向圆柱根部的边界层依然具有很强的涡量,此时槽道控制效果变弱。

图12 对称面流线和涡量云图以及λ2法则提取的空间三维涡结构 Fig.12 Streamlines and vorticity in symmetry of stream field and 3D vortex structure based on λ2-definition
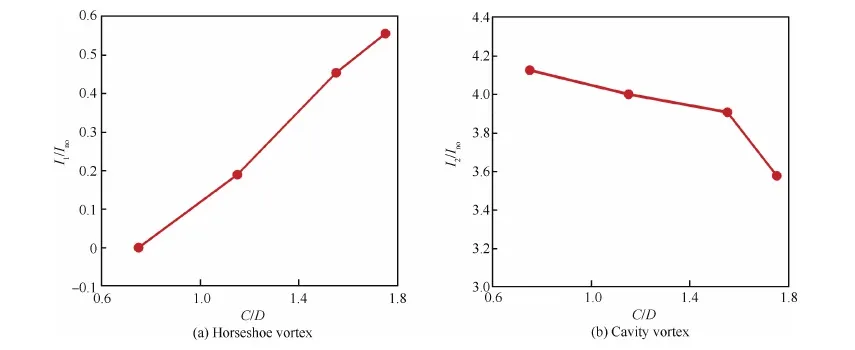
图13 流场对称面处马蹄涡和槽道涡强度随槽道距离参数的变化Fig.13 Change of horseshoe vortex and cavity vortex strength with cavity distance in symmetry of stream field

图14 不同槽道距离下槽道周围流线Fig.14 Local streamlines around cavity with different cavity distance
4 结 论
1) 二维和三维槽道均能减小边界层分离范围,使圆柱根部马蹄涡的强度减弱、尺度减小,同时使槽道上下游逆压梯度下降。
2) 槽道与圆柱的距离参数C对马蹄涡的削弱起到主要作用,随着槽道距离减小,马蹄涡不断减弱,分离范围也不断减小。增加槽道宽度和深度也能增强槽道的控制效果,但增强效果不显著。
3) 槽道的控制机理是由于槽道的抽吸效应使得来流边界层中靠近壁面的高涡量流体被卷吸入槽道,从而使得流向圆柱的流体涡量减小,形成的马蹄涡强度减弱。同时由于三维槽道比二维槽道具有更好的输运槽道涡量的通道,使得三维槽道的控制效果要比二维槽道控制效果好。
[1] DEVENPORT W J, SIMPSON R L. Turbulence structure near the nose of a wing-body junction[C]//19th AIAA, Fluid Dynamics, Plasma Dynamics, and Lasers Conference. Reston: AIAA, 1987.
[2] DEVENPORT W J, SIMPSON R L. Time-dependent and time-averaged turbulence structure near the nose of a wing-body junction[J]. Journal of Fluid Mechanics, 1990, 210(2): 23-55.
[3] DEVENPORT W J, SIMPSON R L. LDV measurements in the flow past a wing-body junction[C]//4th International Symposium on Applications of Laser Anemometry to Fluid Mechanics. Lisbon: Instituto Superior Tecnico, 1988: 2-3.
[4] GRAZIANI R A, BLAIR M F, TAYLOR J R, et al. An experimental study of endwall and airfoil surface heat transfer in a large scale turbine blade cascade[J]. Journal of Engineering for Gas Turbines and Power, 1980, 102(2): 257-267.
[5] BLAIR M F. Heat transfer in the vicinity of a large-scale obstruction in a turbulent boundary layer[J]. Journal of Propulsion and Power, 1985, 1(2): 158-160.
[6] DEVENPORT W J, SIMPSON R L. Time-dependent structure in wing-body junction flows[M]. Turbulent Shear Flows 6. Berlin Heidelberg:Springer, 1989: 232-248.
[7] LIU Z H, XIONG Y, TU C X. Numerical simulation and control of horseshoe vortex around an appendage-body junction[J]. Journal of Fluids and Structures, 2011, 27(1): 23-42.
[8] LIU Z H, XIONG Y. Numerical simulation on the horseshoe vortex formation around the hull-sail junction of submarine[C]//2010 International Conference on Optoelectronics and Image Processing (ICOIP). Piscataway, NJ: IEEE Press, 2010, 2: 51-54.
[9] SEAL C V, SMITH C R, ROCKWELL D. Dynamics of the vorticity distribution in endwall junctions[J]. AIAA Journal, 1997, 35(6): 1041-1047.
[10] KHAN M J, AHMED A. Topological model of flow regime in the plane of symmetry of a surface-mounted obstacle[J]. Physics of Fluids, 2005, 17(4): 1089-1109.
[11] GRECO J J. The flow structure in the vicinity of a cylinder-flat plate junction: Flow regimes, periodicity, and vortex interactions[D]. Bethlehem: Lehigh University, 1990.
[12] PHILIPS D B, CIMBALA J M, TREASTER A L. Suppression of the wing-body junction vortex by body surface suction[J]. Journal of Aircraft, 1992, 29(1): 118-123.
[13] JOHNSON M J, RAVINDRA K, ANERS R. Comparative study of the elimination of the wing fuselage junction vortex by boundary layer suction and blowing[C]//32nd Aerosapce Sciences Meeting & Exhibit. Reston: AIAA, 1994: 10-13.
[14] 徐向南, 张华, 胡波. DBD涡流发生器及其在角区流动控制中的数值研究[J]. 航空学报, 2016, 37(6):1743-1752.
XU X N, ZHANG H, HU B. Numerical study of DBD vortex generator and application in junction flow control[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1743-1752 (in Chinese).
[15] DEVENPORT W J, DEWITZ M B, AGARWAL N K, et al. Effects of a fillet on the flow past a wing body junction[J]. AIAA Journal, 1990, 28(12): 2017-2024.
[16] DEVENPORT W J, SIMPSON R L, DEWITZ M B, et al. Effects of a leading-edge fillets on the flow past an appendage-body junction[J]. AIAA Journal, 1991, 30(9): 2177-2183.
[17] NELSON R, GEORGE E, HAMID R. Effects of an upstream ribbed surface on the flow past a cylinder-flat plate junction[C]//AIAA 41st Aerospace Sciences Meeting and Exhibit. Reston: AIAA, 2003.
[18] KAIROUZ K A, RAHAI H R. Turbulent junction flow with an upstream ribbed surface[J]. International Journal of Heat and Fluid Flow, 2005, 26(5): 771-779.
[19] HORSTEN B, VELDHUIS L. Experimental and numerical results on cavity effects in juncture flow[C]//AIAA 38th Fluid Dynamics Conference and Exhibit. Reston: AIAA, 2008.
[20] KANG K J, KIM T, SONG S J. Strengths of horseshoe vortices around a circular cylinder with an upstream cavity[J]. Journal of Mechanical Science and Technology, 2009, 23(7): 1773-1778.
[21] ZAW ZAW O O. The investigation and control of 3D separated structures in juncture flow[D]. Beijing: Beihang University, 2011.
[22] ANSYS Inc. ANSYS FLUENT user’s guide[M]. 2012.
(责任编辑: 李明敏)
Junction flow horseshoe vortex control based on upstream cavity
LIJian,ZHANGHua*,WUXinggang
SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China
Two and three dimensional cavities have been studied by experimental and numerical simulation to control horseshoe vortex formed when the flow passes a cylinder-flat plate junction. The cavity is located on the flat plate upstream of the cylinder. The results indicate that both two and three dimensional cavities can delay boundary layer separation and weaken the horseshoe vortex. At the same time, the upstream surface pressure and adverse pressure gradient of cavity are both reduced, and at the downstream the pressure is increased while the global adverse pressure gradient is reduced. The study also indicates that the two dimensional cavity can reduce about 61.15%-66.51%, while the three dimensional cavity can reduce 66.65%-80.93%, of the horseshoe vortex strength. The effect of cavity geometry parameters, including distance, width and depth, is discussed. It is shown that the cavity distance plays major role in weakening the horseshoe vortex. The mechanism for controlling the horseshoe vortex by cavity is discussed. It is shown that the sub-layer of the incoming boundary layer which contains high vorticity is swallowed into the cavity to form the cavity vortex. The cavity vortex is transported to the downstream of the junction. As the cavity gets closer to the cylinder, more sub-layer of boundary layer will be swallowed into cavity. It is this cavity-effect that reduces the surface adverse pressure gradient upstream of the cylinder and diminishes the horseshoe vortex and separation region.
junction flow; horseshoe vortex; flow control; upstream cavity; particle image velocimetry test
2016-09-18;Revised2016-11-13;Accepted2016-11-21;Publishedonline2016-11-301518
URL:www.cnki.net/kcms/detail/11.1929.V.20161130.1518.004.html
NationalNaturalScienceFoundationofChina(11372027)
2016-09-18;退修日期2016-11-13;录用日期2016-11-21; < class="emphasis_bold">网络出版时间
时间:2016-11-301518
www.cnki.net/kcms/detail/11.1929.V.20161130.1518.004.html
国家自然科学基金 (11372027)
*
.E-mailltszhh@buaa.edu.cn
李健, 张华, 吴星钢. 利用上游槽道对角区马蹄涡的控制J. 航空学报,2017,38(6):120796.LIJ,ZHANGH,WUXG.JunctionflowhorseshoevortexcontrolbasedonupstreamcavityJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120796.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0304
V211
A
1000-6893(2017)06-120796-11
*Correspondingauthor.E-mailltszhh@buaa.edu.cn
