探讨外露式钢结构柱脚反力计算
2017-11-20曾艺鑫
曾艺鑫
(建发房地产集团—南平事业部 福建南平 353000)
探讨外露式钢结构柱脚反力计算
曾艺鑫
(建发房地产集团—南平事业部 福建南平 353000)
由于现有钢结构设计文献均未详细阐述柱脚反力的计算方法,规范更是没有相应的计算公式。在设计实践中,设计人员缺乏相应的理论作为技术支持,这样不利于设计计算的修改和对计算结果的判断。基此,文章论述了外露式钢结构柱脚的反力计算原理,得出在不同条件下,锚栓拉力、混凝土应力的计算方法。
外露式钢结构柱脚;钢柱脚反力
0 引言
对大部分钢结构设计人员耳熟能详的经典设计手册中,关于柱脚反力计算的手册为文献[1]第291页提出的3种受力状况下的底板及柱脚锚栓的反力公式。该文献对3种受压状态均提出了有效的计算公式,但缺少偏心受拉的计算公式。同时,它也是MTSTool工具箱在受压工况的下的设计依据。然而MTSTool工具箱无论轴力输入的是正是负,均按偏压计算,因而无法用于偏拉工况的计算。
文献[2]第501页提出了大偏心受压受压时的底板反力计算,它仅仅提供了变形协调的方程,并要求读者自行结合内力平衡进行计算,存在公式片面不全,设计无法采用,以及算法仅考虑大偏压。
文献[3]第4页在推导的公式出现了混凝土受拉的不合理结果,同时给出的表格均为柱脚受压的结果,无法满足工程设计的需要。
对PKPM结构设计软件的偏拉计算结果,进行复核,复核其在偏拉工况下的混凝土受压区高度,超过其底板高度,结果明显不合理。
基此,本文将系统的阐述外露式钢柱脚在小偏心受压、大偏心受压、小偏心受拉、大偏心受拉状态下的柱脚反力计算原理,并提出计算公式。计算理论的推导,均假定柱脚锚栓只受拉不受压、底板下的混凝土只受压不受拉,同时底板变形按平截面假定考虑。
1 小偏心受压时,状态1的柱脚反力计算
小偏心受压是以受拉区锚栓受拉与否为标志,柱脚锚栓不受拉(其受力为零)为小偏压。此时,底板混凝土为全截面受压或者存在部分零应力区。状态1为全截面受压,状态2为局部受压且受拉侧锚栓不受拉,如图1~图2所示。
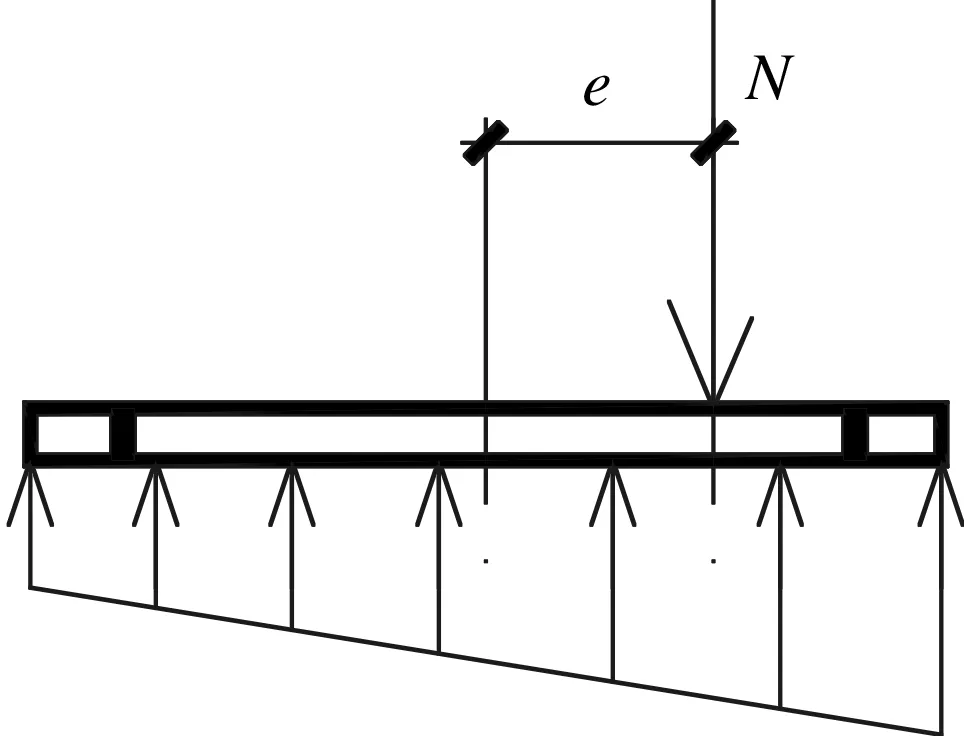
图1 小偏压状态1注:底板全截面受压
根据材料力学:
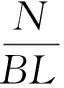
(1)
其中σc为混凝土应力,受压为正,B为底板宽度,L为底板长度。当公式中的加减符号取负号时,混凝土最小应力应为压应力,所以:
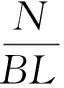
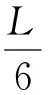
(2)
因此,小偏心受压状体1时混凝土的最大压力按(1)符号取正号,判别方程为(2),而柱脚锚栓总反力为零:Ta=0。
2 小偏心受压时,状态2的柱脚反力计算
小偏心受压状态2时,底板存在局部的零应力区,受压区超过受拉锚栓的位置,而锚栓位置混凝土仍受压,其反力分布如下:
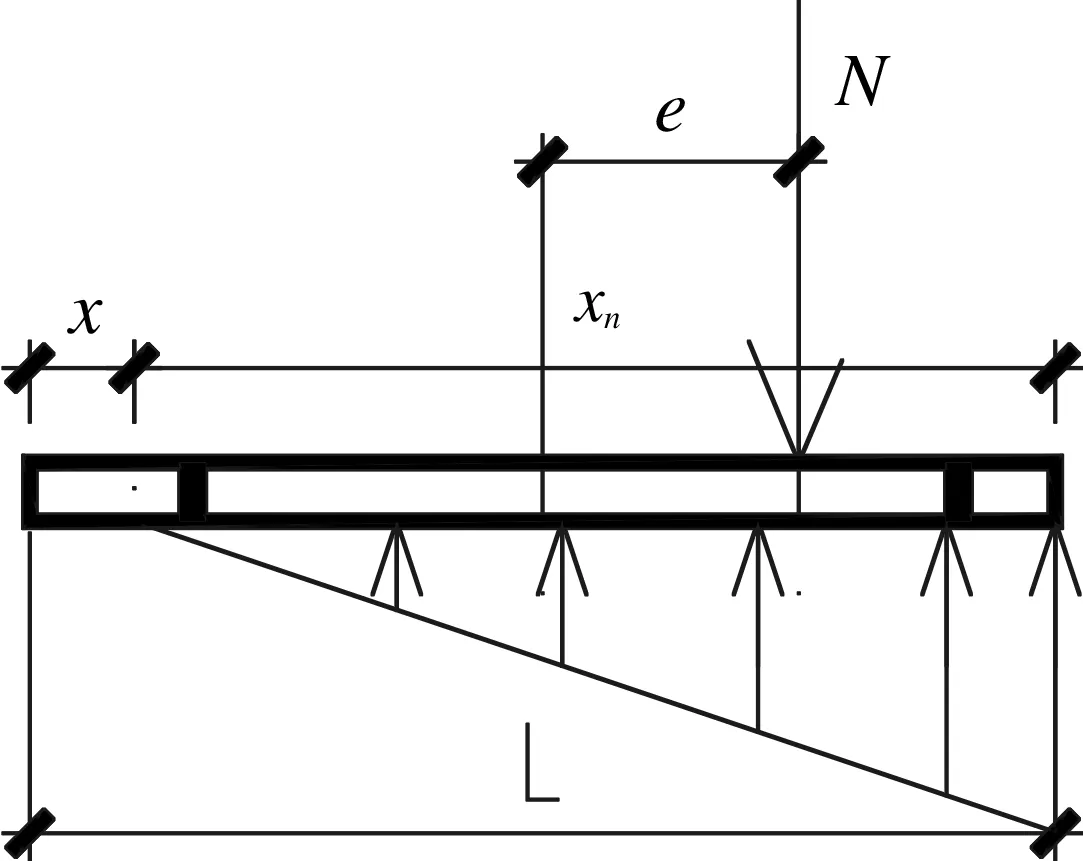
图2 小偏压状态2注:底板存在零应力区
根据力的平衡方程:
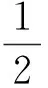
(3)
其中x为混凝土零应力区长度,xn为受压区长度。
三角形混凝土反力的合力点应与N作用点重合:
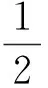
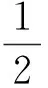
(4)
则混凝土受压区长度xn:
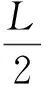
(5)
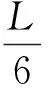
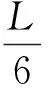
(6)
因此,小偏心状态2的判别方程为公式(6),受压区长度按公式(5)。柱脚锚栓总反力为零:Ta=0,在求得受压区长度xn后,再根据公式(3)即可求得最大的混凝土压应力。
3 大偏心受压时,柱脚反力计算
文献[1]第291页提出了大偏心受压的计算方程和求解方程所需的图表,但没有给出推导过程,这里着重给出推导过程,为下文推导大偏心受拉公式做铺垫。根据应变图3可得:

图3 大偏心受压时,底板反力图
整理后可得变形协调方程:
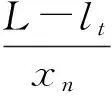
(7)
由图4底板反力分布图可得:
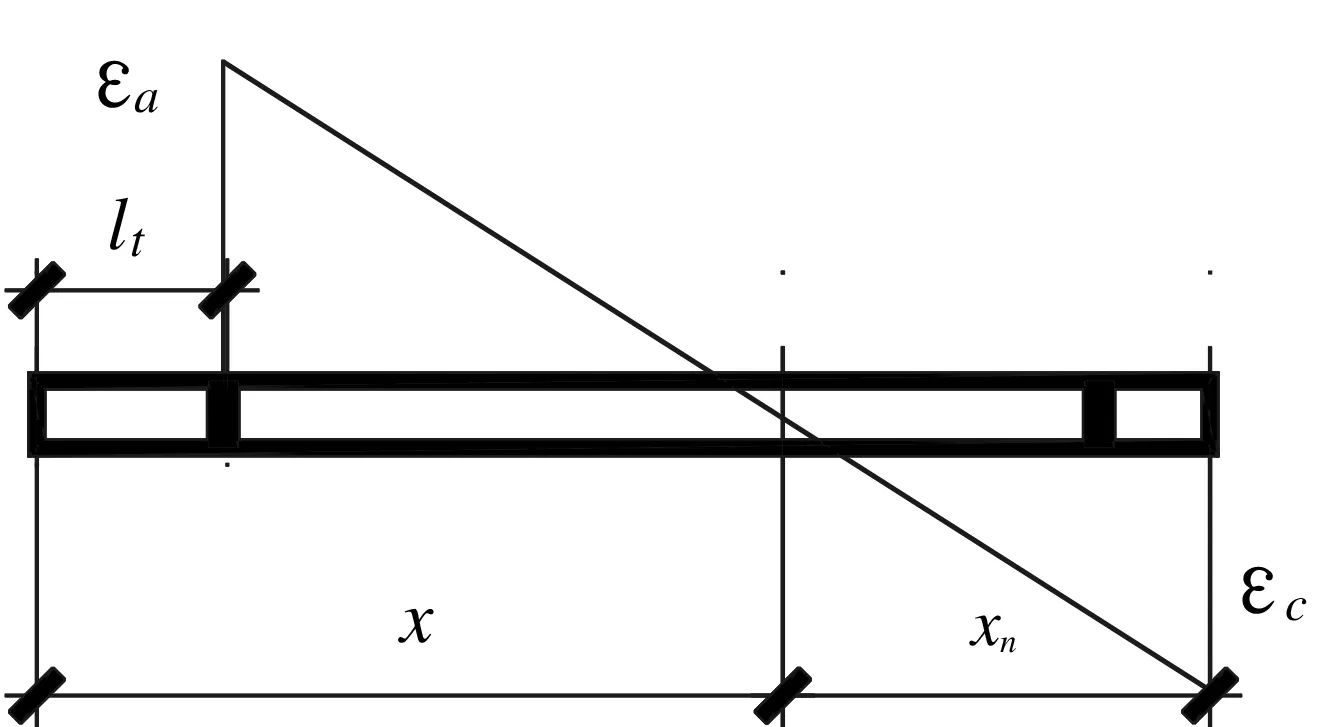
图4 大偏心受压时,底板应变图
力的平衡方程:
(8)
对混凝土合力点取矩可得:
(9)
M为柱脚弯矩。
将(8)直接代入(9),可得:
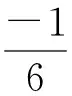
(10)
将应力方程式(7)代入力的平衡方程式(8):
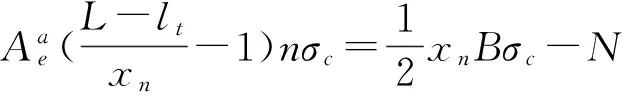
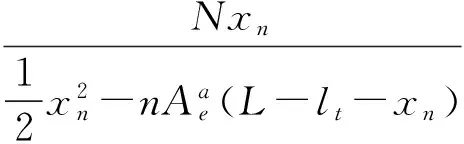
(11)
其中N为柱脚压力,受压为正。
将式(11)代入式(10)可以得到一个一元三次方程,未知数为 :
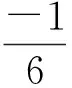
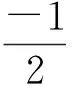
整理后可得:
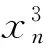
(12)
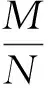
式(12)与文献[1]结果一致。
大偏心受压柱脚的计算过程为根据式(12)求得受压区高度xn,然后根据式(11)求解混凝土最大压应力σc,再根据合力式(8)求解锚栓拉应力σa。由上文不难得出大偏心受压的判定条件为:
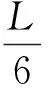
(13)
4 小偏心受拉时,柱脚反力计算
由图5可知,小偏心受拉时,底板混凝土全截面为零应力区,柱脚拉力全部由柱脚锚栓承担,根据材料力学(类似桩基反力公式)可得一根锚栓的力为:
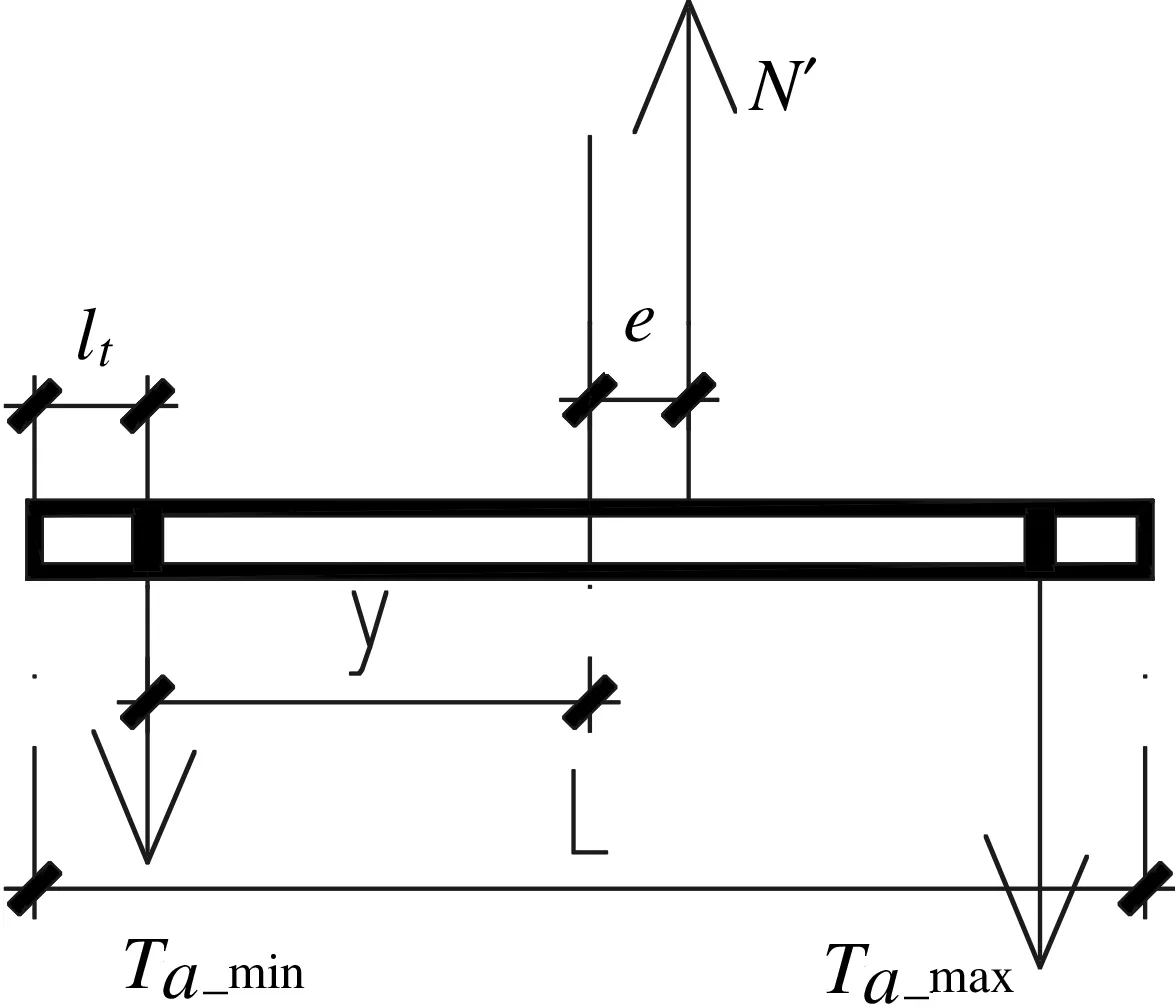
图5 小偏心受拉
(14)
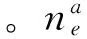
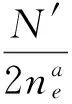
(15)
不满足式(15) 的偏拉就是大偏拉。
5 大偏心受拉时,柱脚反力计算
图6为大偏心受压拉时底板反力图,图7为大偏心受压时底板应变图。
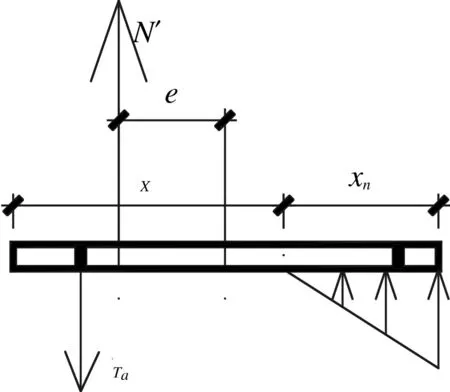
图6 大偏心受拉时底板反力图
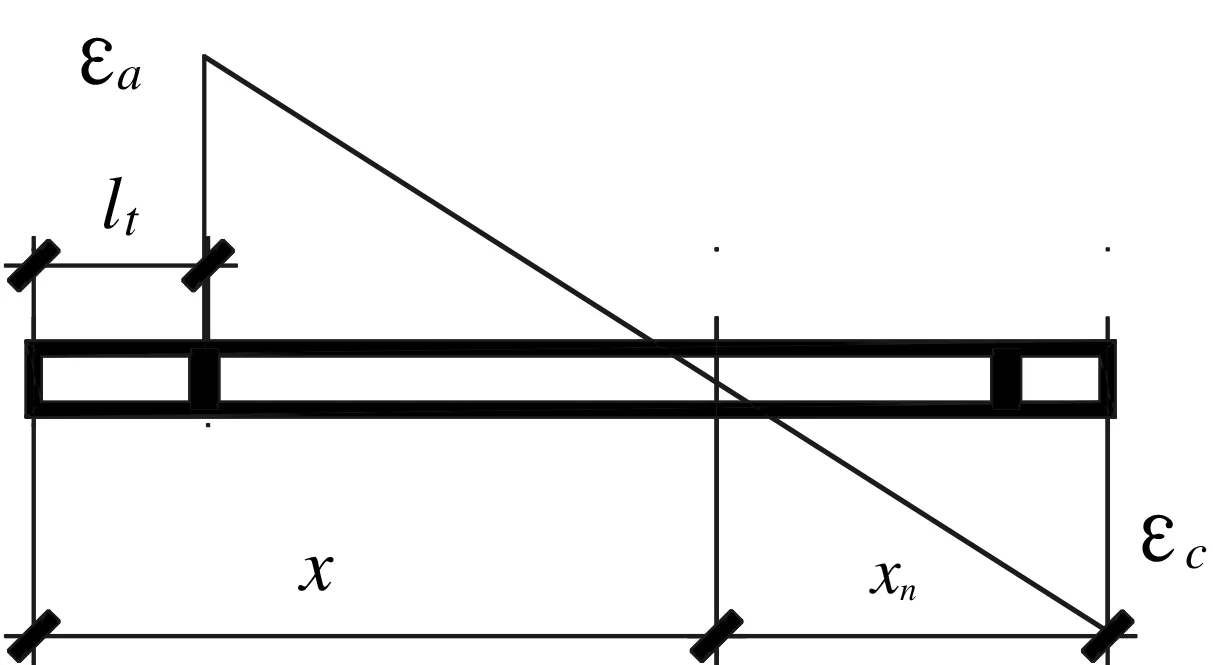
图7 大偏心受压时底板应变图
根据应变图7可得:
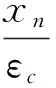
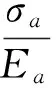
整理后可得变形协调方程:
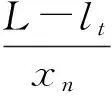
(16)
由图6(底板反力分布图)可得力的平衡方程:
(17)
对混凝土合力点取矩可得:
(18)
其中N′为柱脚拉力,受拉为正,其余符号说明同上文所述。
将式(17)与式(8)对比,式(18)与式(9)对比不难发现,如果柱脚力一律以N表示,受压取正,而受拉取负,则力的平衡方程和弯矩方程可以表达为:
(19)
对混凝土合力点取矩可得:
(20)
而大偏拉的变形协调方程与大偏压的应力方程完全相同且不含轴力项,二者的合力方程与弯矩方程表达形式一样。因此,大偏拉求解受压区高度xn的一元三次方程不必另行推导,其结果与大偏压一致,即可表达为:
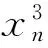
(21)
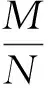
根据第五节,大偏拉的判定条件为
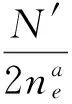
(22)
对于同样大小的柱底轴力,受压、受拉时,三元一次方程式(21)的系数随着N的正负的不同而不同。
6 现有计算方法的缺陷
给定相同的算例的条件,分别按MTSTool工具箱、PKPM工具箱和论文方法计算方法进行计算。条件为:轴力为230kN(分别按压、拉进行),弯矩为250 kN·m。由于PKPM柱脚软件在给定内力后会自动确定所需的底板尺寸和锚栓规格,因此在偏拉和偏压下底板尺寸和锚栓规格按PKPM生成的结果进行计算(这也是PKPM工具箱的不便之处,无法灵活调整底板尺寸和锚栓规格,不方便设计调整)。
偏压的计算条件和结果如表1所示,可见3种计算结果基本一致。
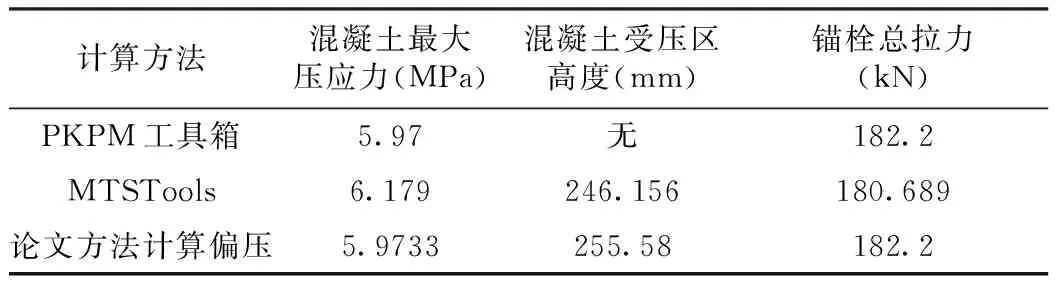
表1 偏压计算结果
注:底板尺寸540mm×990mm,翼缘处锚栓为4M24,lt=50mm。轴力为230kN(压力,偏压)弯矩250kN·m。
偏拉的计算条件和结果如表2所示,可见3种计算结果相差甚大。
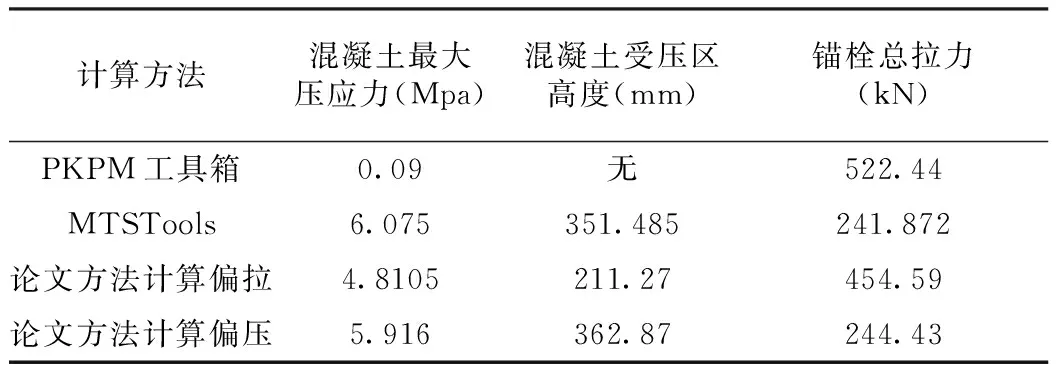
表2 偏拉计算结果
注:底板尺寸442×930mm,翼缘处锚栓为2M56,lt=110mm。轴力为-230kN(拉力,偏拉),弯矩250kN·m。
首先分析MTSTool工具箱,无论轴力取正取负,其输出的混凝土受压区高度、混凝土最大压应力均相同,这是不正确的。而且,其结果和表2中的论文方法计算偏压的结果接近:锚栓总拉力分别为241.872kN(MTSTools)和244.43kN(论文方法计算偏压)。混凝土压应力分别为6.075MPa(MTSTools)和5.916MPa(论文方法计算),通过以上两点分析可见,它将偏拉当做偏压考虑。
PKPM工具箱的结果混凝土压应力为σc,pkpm=0.09MPa,锚栓总拉力为522.44kN。在不考虑腹板锚栓的情况下,以合力为零求解混凝土受压区高度(如果腹板锚栓受压,则不考虑其作用,反之如果受拉,则混凝土受压区高度将比目前计算的要大):
230kN+σc,pkpm442mm×x=522.44kN
x=7.351m超过底板的高度930mm甚多,如果考虑上腹板螺栓,或按三角形应力图形考虑,则受压区高度更高,因此PKPM工具箱的偏拉结果无法通过复核。它无法满足合力平衡方程。
上述文献计算方法在求解大偏压时,结果与这两款软件一致,而大偏拉计算只需将轴力取为负号,同时文献计算方法还根据计算结果复核合力平衡方程和弯矩平衡方程,均是接近零的小数,因此文献计算方法计算结果是正确的。碍于篇幅所限,无法一一列举各个工况下的计算结果对比,本节所举例的分别为大偏压和大偏拉。
7 结论
小偏压时柱脚反力可按本文1~2节、小偏拉时柱脚反力可按本文第4节提供的公式和判别方程计算。大偏压时柱脚反力可按第3节内容进行计算,其一元三次方程的求解可以采用二分法计算。大偏拉的计算方法与大偏压相同,不过是将轴力取负。计算结果最后应以满足变形协调方程(大偏拉、大偏压需满足)、合力方程、弯矩方程作为检验标准。
在轻型钢结构柱脚设计中,偏拉工况是控制柱脚底板尺寸和锚栓规格的决定因素,既有钢结构工具箱在计算这一工况时存在不同程度的缺陷:即将偏拉当做偏压考虑或者是计算结果经不起复核。
[1] 李星荣,魏才昂,丁崎崐,等.钢结构连接节点计算手册[M].北京:中国建筑工业出版社,2005.
[2] 《钢结构设计手册》编辑委员会.钢结构设计手册[M].北京:中国建筑工业出版社,2011.
[3] 中国建筑标准设计研究院.单层房屋钢结构节点构造详图(06SG529-1) [M].北京:中国计划出版社,2006.
DiscussiononCalculationofReactionForceofExposedSteelColumnbriefly
ZENGYixin
(C&D Real Estate Corporation Limited,Nanping 353000)
There is not specific description of calculation method and standard formula of the column base counterforce in the existing steel structure design documents. Therefore, for lack of the corresponding theory as technical support, it will go against the modification of a design and the judgement of the results of a calculation for designers. Here we discussed the calculation principle of exposed steel structure column counterforce, and concluded the calculation method of anchor tension and concrete stress under different conditions
The exposed type steel structure column; Steel column base counterforce
TU391
A
1004-6135(2017)10-0039-04
曾艺鑫(1982.9- ),男,工程师。
E-mail:badbull22545@sina.com
2017-06-09
