考虑放宽静稳定度的民用客机气动优化设计

李立， 白俊强,*， 郭同彪， 陈颂

1.西北工业大学 航空学院， 西安 710072 2.湖北航天飞行器研究所， 武汉 430040

考虑放宽静稳定度的民用客机气动优化设计

李立1， 白俊强1,*， 郭同彪1， 陈颂2

1.西北工业大学 航空学院， 西安 710072 2.湖北航天飞行器研究所， 武汉 430040

为了更加有效地减小民用客机考虑配平约束后的阻力，针对典型跨声速民用客机机翼-机身-平尾构型研究了不同静稳定度下的气动优化设计，并总结出在民用客机的减阻设计中考虑放宽静稳定度具有较大的减阻潜力。通过自由型面变形(FFD)技术对全机外形进行参数化，实现机翼型面的变形，进行气动优化设计并改变平尾的偏转保证全机能够力矩配平。采用基于雷诺平均Navier-Stokes(RANS)方程的离散伴随方法求解目标函数对设计变量的梯度，然后基于序列二次规划算法进行基于梯度的气动优化设计。基于CRM(Common Research Model)构型，针对不同参考重心位置进行了考虑配平约束的减阻优化设计研究，验证了优化设计系统的有效性，算例结果表明，随着重心位置后移即放宽静稳定度，优化构型配平阻力减小，外翼段前缘吸力峰值明显降低且双激波的强度得到有效减弱，此外机翼的升力系数分布更加贴合最佳升力系数分布。

放宽静稳定度； 离散伴随； 气动优化设计； 配平阻力； 升力系数分布

提升飞机飞行性能并有效降低油耗是目前民用飞机设计研究的重要课题，而减小全机阻力是完成这些任务的最有效手段之一。具体来说，降低全机阻力可以从以下两个方面考虑[1]。一方面是减小配平阻力。飞机在任何飞行状态下都处于配平状态，即绕重心的力矩为0。通常来说，民用客机都是有静稳定裕度的，为了保证飞机配平，后置平尾会通过负偏转产生一个负升力，以提供一定的抬头力矩使得飞机配平，此时就会导致机翼上有一个正升力的增量，来保证全机总升力系数不变。这一正升力的增量会使得机翼产生一个升致阻力增量, 连同平尾产生的升致阻力增量, 一起被称为飞机的配平阻力[2]。另一方面是降低翼身组合体的激波阻力和压差阻力等。对于前者，通常是减小翼身组合体或者平尾的型阻来实现配平阻力的降低，但对后平尾飞机而言，通过向后移动全机重心也可以实现配平阻力的减小，这样的设计被称为放宽静稳定度设计；对于后者，可以通过合理优化机翼型面和调整机翼的载荷分布来实现阻力的减小。

国内外对考虑静稳定度影响的飞行器设计已经进行了大量的研究：Lutze提出了不同重心位置对于全机气动力和几何参数产生影响的解析表达式，研究了如何有效减小全机配平阻力[1]；Sachs推导出机翼下洗对机翼/平尾干扰阻力的分析表达式，并基于此阐述了最小配平阻力和全机最优重心的关系[3]；王子方用工程估算的方法分析了放宽静稳定对改善飞机性能的影响及其气动原理[4]；周慧钟和李忠应分析了放宽静稳定度可能对飞行器带来的影响以及放宽静稳定度后飞行器本身的动态特性[5]；许维进和刘志敏为了研究如何降低飞机配平状态下阻力的问题，推导了飞机升致阻力与重心位置间的关系式，并得到通过向后移动重心位置实现放宽静稳定度应在飞机设计初期就加以考虑的结论[2]；王华友等讨论了飞机放宽纵向静稳定度后, 重心后移量对飞机纵向气动参数的影响, 以及由此所引起的飞机配平迎角、平尾偏角及基本飞行性能的变化[6]；冯小刚等介绍了放宽静稳定性技术、实现途径和放宽程度分析，归纳了静稳定度放宽后对飞机带来的影响[7]。但是，综合国内外来看，针对民用宽体客机，均没有实现考虑放宽静稳定度的机翼气动优化设计，无法充分挖掘设计结果在考虑放宽静稳定度后的全机减阻收益，也无法保证考虑放宽静稳定度后的构型有较好的气动性能。

优化算法是气动外形优化设计的顶层架构，由于其能控制整个优化设计的运行和方向，因而需要合理选择。非梯度类优化算法虽然开发难度低、鲁棒性较好、理论上可以收敛到全局最优解，但优化周期较长，计算量代价大，且对于大规模设计变量处理效率并不高效[8]。基于梯度法的气动优化设计由于可高效迭代求解快速收敛到局部最优解而受到很大关注，而且Lyu等的研究指出梯度法求解的不同局部最优解之间非常接近，气动阻力相差在0.1个阻力单位以内[9]，此外，优化过程中对目标函数的调用次数比较少，处理大规模设计变量时其计算量与设计变量个数之间可实现基本解耦，并且能够处理大规模约束条件。因此，应用伴随方程法是基于梯度算法进行大规模设计变量气动外形优化设计的较好选择[10-11]。目前国外许多航空航天研究机构以及高校都针对基于伴随方程的梯度法气动优化设计开展了大量研究工作，而且开发形成了一批实用的软件工具，如美国斯坦福大学飞行器设计实验室开发的SU2开源程序软件[12]、法国宇航院(ONERA)开发的elsA软件[13]、德国宇航研究院(DLR)开发的Tau软件[14]等。国内在该方面的研究工作起步较晚，西北工业大学[15-16]、南京航空航天大学[17-18]、中国空气动力研究与发展中心[19-20]等开展了相关的工作，获得了一定的研究成果。但尚未应用于考虑放宽静稳定度的机翼气动优化设计中。

本文针对大型民用宽体客机全机构型考虑放宽静稳定度的优化设计问题，以CRM(Common Research Model)标模作为研究对象，采用基于伴随方程法的梯度优化算法进行了气动减阻优化设计。通过改变全机的参考重心位置来改变全机静稳定度，针对不同静稳定度的情况，通过机翼型面的变形进行气动优化设计并利用平尾的偏转最终保证本文实现的全机设计结果满足配平约束条件。算例表明了优化设计系统的可行性，并对比研究了不同静稳定度对全机气动特性的影响，证明了民机气动减阻设计考虑放宽静稳定度具有较大的减阻潜力。

1 基于FFD技术的气动外形参数化

气动外形参数化方法是将飞行器的气动外形通过一定的函数关系，映射为一组设计参数(即设计变量)，设计者可以通过改变这些参数或变量的值，对气动外形进行操作。实用的气动外形参数化方法要求能够采用较少的参数来定义几何外形，并且保证一定精度，同时提供充分的设计空间，能够描述尽可能丰富的外形变化。

本文采用自由型面变形(FFD)方法对研究对象进行参数化建模，该方法以弹性体受力后变形的思想实现几何参数化过程[21]。由于FFD方法参数化对象为几何的空间变化量，因此不需要拟合研究对象的初始构型。且该方法能保证几何的光滑连续性，从而能准确方便地描述研究对象的整体和局部几何信息。

对研究对象进行FFD方法参数化建模的过程为：首先，在待变形的研究对象周围选取空间控制点，连接组成FFD控制体，如图1所示。然后，建立研究对象与控制体顶点之间的映射关系，此过程研究对象和控制体处于同一个空间坐标系，称为全局坐标系，而控制体上建立局部坐标系。本文选取了基于Bernstein多项式的FFD方法，针对研究对象上任一点，都是通过式(1)实现全局坐标与局部坐标之间的映射关系，表达式为

XFFD(s,v,u)=

(1)

式中：XFFD(s,v,u)为研究对象上任一点在全局坐标系下的坐标值，s、v、u为该点在控制体内的局部坐标值；Pi,j,k为FFD控制点的全局坐标；Bil(s)、Bjm(v)、Bkn(u)分别为l、m、n次Bernstein多项式基函数。在变形过程中，即FFD控制点的全局坐标产生一个位移量时，研究对象任一点的局部坐标保持不变，通过式(1)的映射关系得到该点变形后的全局坐标，即可得到变形后的几何外形。

本文采用FFD方法是为了实现机翼的气动外形参数化和平尾的整体偏转。对于机翼，控制机翼型面的FFD控制点共有380个(图1中蓝色控制点)，其中沿展向分布10个，沿弦向分布19个，垂直于弦向2个。对于平尾，其整体偏转是通过让包围它的FFD控制体绕给定的转轴(图2中红色线)旋转实现的，其中给定转轴的定义参考实际飞机的平尾偏转，为平尾翼根和翼梢40%弦向处连接而成的直线。图2为平尾绕给定转轴旋转±5° 的对比示意图，可见平尾FFD控制体的整体偏转实现了其包围的平尾表面网格相应的转动，转动后平尾翼根与机身的网格仍然正常连接，也说明本文采取的FFD方法可有效实现平尾的偏转从而进行考虑配平约束的优化设计。

图1 全机构型的FFD控制体Fig.1 FFD control framework for aircraft

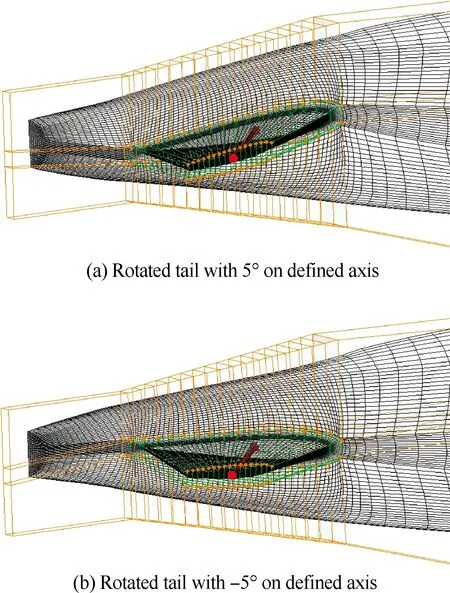
图2 FFD控制体对平尾实现偏转Fig.2 Rotated tail by FFD control frame

2 流场数值求解

本文采用雷诺平均Navier-Stokes(RANS)方程作为流场控制方程进行流场数值求解，其守恒形式的表达式为

(2)

式中：U为流场守恒变量；F1、F2、F3为无黏通量项；G1、G2、G3为黏性通量项。流场数值计算采用全湍计算求解，湍流模型为S-A(Spalart-Allmaras)。空间离散格式为二阶中心差分格式，时间推进采用LU-SGS (Lower-Upper Symmetric Gauss-Seidel) 方法隐式求解。

本文选取的研究对象是NASA第四届和第五届阻力预测会议的CRM构型，是典型的跨声速民用宽体客机构型，其力矩参考点在全机平均气动弦长的25%处，坐标为x= 33.677 9 m,y=0 m,z=4.519 93 m，机翼半展长为29.4 m，参考面积为191.84 m2[22]。本文为验证所采用的流场数值求解方法的准确性，以CRM标模作为计算对象，以CRM构型的典型试验状态[23](马赫数Ma=0.85，升力系数CL=0.485)进行气动特性对比校验。在验证求解和之后的优化设计过程中，采用的CFD计算网格规模均为600万。计算结果与试验结果的典型剖面压力系数Cp分布对比如图3所示，c为弦长，可看出计算结果与试验结果吻合良好，说明本文所采用的CFD流场数值求解方法准确可靠，可用来进行数值优化设计。

图3 试验与本文方法计算的压力系数分布对比Fig.3 Comparison of pressure coefficients distribution obtained by experiment and the present method calculation

3 离散伴随方程法

离散伴随方程法直接从已经离散的目标函数及流场控制方程出发，可以获得基于离散的目标函数和流场解的数值精确导数，且边界条件无需特殊处理，因此本文采用离散伴随方程求解气动目标函数对设计变量的梯度。

气动目标函数W通常包括力系数、力矩系数等，可通过对表面网格的每一个单元积分得到。构建目标函数表达式为

W=W(U(τ),G(τ))

(3)

式中：τ为一组关于气动外形的设计变量；G(τ)是由设计变量决定的CFD计算网格。当给定设计变量τ时，通过参数化方法可确定描述气动外形的表面网格，继而根据动网格算法可以求得对应的空间网格，最终通过求解可获得流场解向量U(τ)，因此式(3)中气动目标函数W写成关于解向量U(τ)和计算网格G(τ)的形式。

当流场数值求解得到稳定收敛的流场解向量时，式(2)可写为在空间网格离散后的流动控制方程组，即

R=R(U(τ),G(τ))=0

(4)

将式(3)和式(4)分别对τ求全导数可得

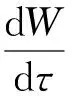
(5)

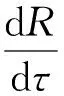
(6)

将式(6)代入式(5)有

(7)

如果对式(7)每一项单独求解，则会涉及到矩阵求逆项(∂R/∂U)-1，由于对大规模的矩阵求逆将会带来巨大的计算消耗，所以设伴随变量ψ，使得

(8)

此时可以将矩阵求逆项转化为求解线性方程组，即转化为求解伴随变量：

(9)

此时，式(7)可以写为

(10)

以上推导即利用离散伴随方程法求解气动目标函数对设计变量的梯度的过程。式(10)中，∂W/∂G为目标函数对计算网格的偏导数，在收敛流场解的基础上求偏导即可；∂R/∂G为流场残差对计算网格的偏导数，在流场计算中可求得该项；dG/dτ为计算网格对设计变量的偏导数，由参数化方法和动网格变形算法确定。而由于伴随方程式(9)本质是一个大规模、高度稀疏的线性方程组，因此式(10)准确高效求解的计算量主要体现在对该方程组的求解，本文采用广义最小残量(General Minimum RESidual, GMRES)算法[24]来进行伴随方程的求解。

4 优化设计系统

本文建立的优化设计系统主要由以下模块组成：基于FFD技术的气动外形参数化模块、网格变形模块、流场数值求解模块、伴随方程模块和梯度优化算法模块。其中梯度优化算法模块中的梯度优化算法选用序列二次规划(Sequential Quadratic Programming， SQP)算法[25]，该算法能迅速收敛到局部最优解，优化过程中对目标函数的调用次数比较少，且能够处理大规模函数约束条件。具体优化流程如图4所示。

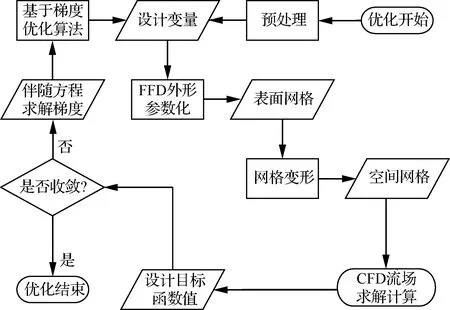
图4 优化设计系统流程Fig.4 Flowchart of optimization design system

5 考虑不同静稳定度的全机构型优化设计

本文针对CRM机翼-机身-平尾构型开展考虑静稳定度涉及多约束的气动减阻优化设计。通过移动飞机的参考重心(c.g.)位置来改变飞机的静稳定度，本文分别选取全机平均气动弦长的15%、20%、25%、30%和35%处作为飞机参考重心，x坐标具体位置分别为32.977 37 m,33.327 635 m,33.677 9 m,34.028 165 m和34.378 43 m,而y和z坐标都保持为0 m和4.519 93 m。

针对每一个参考重心位置，进行此静稳定度下的气动优化设计，优化的设计点状态为马赫数Ma=0.85，升力系数CL=0.5，雷诺数Re=40.0×106，优化目标为阻力系数CD最小，优化设计变量包括来流迎角α、机翼FFD控制点的z向位移ω(共380个设计变量)以及偏转平尾FFD控制体的扭转角η。

minCD_Ma0.85

Vary:ω,α,η

(11)

5.1 优化设计结果对比

不同参考重心位置下，优化前后设计点的机翼上表面压力系数Cp分布对比如图6所示，从图中可看出，初始构型机翼上表面均有明显的激波，通过优化，激波得到有效抑制并基本消除。

图5 初始构型和优化构型气动特性对比(Cm=0)Fig.5 Comparison of aerodynamic performance of initial and optimized configurations (Cm=0)

图6 初始和优化构型压力系数分布对比Fig.6 Comparison of pressure coefficients distribution of initial and optimized configurations

5.2 考虑不同静稳定度优化设计减阻分析

本小节将讨论考虑不同静稳定度优化设计的具体减阻收益：针对初始和优化后考虑配平的构型，在不同参考重心位置下，对比分析机翼典型剖面的压力分布以及对比研究机翼和平尾升力系数分布的影响。

图7为初始构型在不同参考重心位置下机翼的剖面压力系数分布对比图，图8为初始构型在不同参考重心位置下机翼和平尾升力系数分布对比图，其中横坐标y表示沿机翼展向的距离。

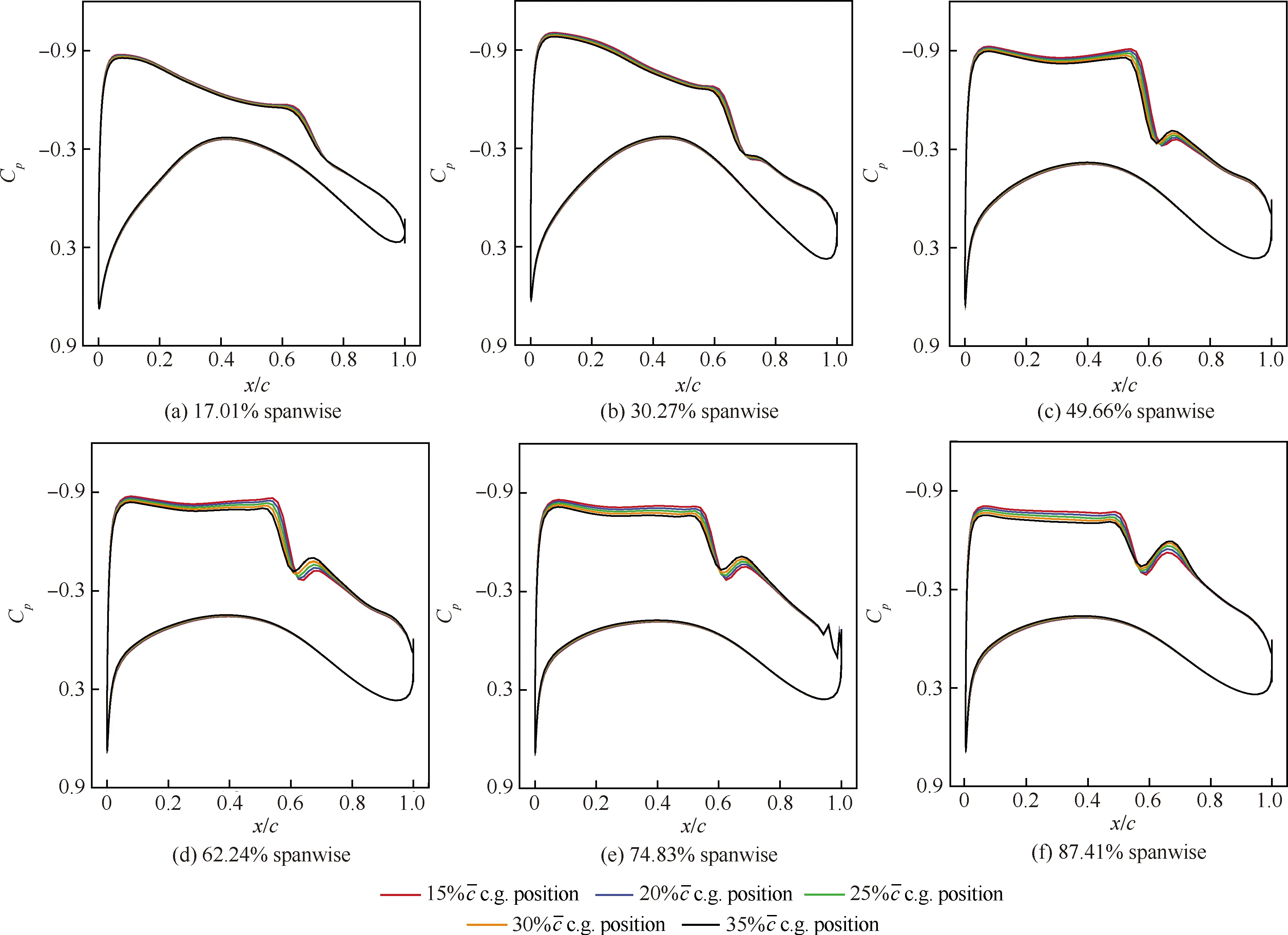
图7 初始构型机翼剖面压力系数分布对比Fig.7 Comparison of wing section pressure coefficients distribution among initial configurations

由于此时初始构型只能通过平尾旋转实现配平，因此，图7中机翼表面压力分布趋势基本一致，而从图5和图8中可以得出，当重心位置后移时，平尾负升力减小，机翼正升力也减小(维持全机总升力系数)，导致机翼和平尾的升致阻力均减小，这就是此时配平阻力有效减小的原因，故可得出对于民用客机构型，仅通过后移其参考重心位置即放宽其固定静稳定度就可有效实现减阻。

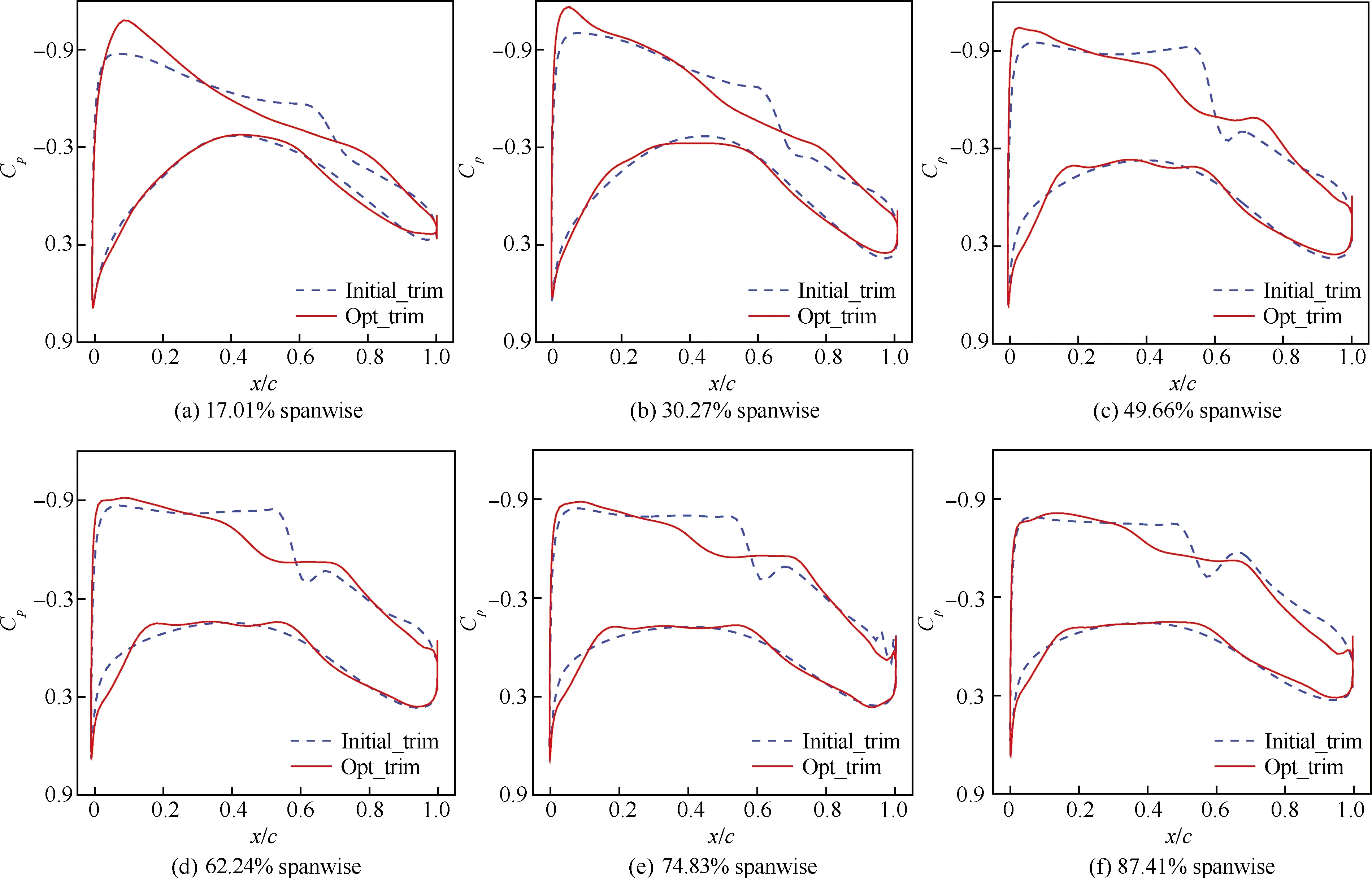
图9为在不同参考重心位置下优化构型机翼的剖面压力系数分布对比。图10为在不同参考重心位置下优化构型机翼和平尾升力系数分布对比。图11～图15为在每一个参考重心位置下优化前后构型机翼的剖面压力系数分布对比。通过图11～图15首先可以看出在每一个参考重心位置下，优化构型均实现了不同程度的激波强度减弱，都表现出内翼段激波强度明显减弱，外翼段双激波压力分布形态得到改善，第一个激波的强度明显减弱，即相对于初始构型，优化构型有效减小了激波阻力；而对于不同的参考重心位置，通过图9 对比可以看出，随着重心位置后移，激波减弱程度也越来越大，特别是外翼段前缘吸力峰值明显降低和双激波的强度越来越弱，即激波阻力减小越来越多；此外，从图10中可得出(图中“Elliptical lift coefficient”为根据机翼椭圆形环量分布得到的最佳升力系数分布)随着重心位置后移的优化构型，平尾负升力减小，机翼正升力也减小(图5中的升力系数对比可看出具体数值变化)，说明配平阻力不仅有效减小而且减小程度越来越大，此外，机翼升力系数分布更加贴合最佳升力系数分布，这是因为随着重心后移，优化为了满足配平约束首先会使得机翼载荷外移减小重心后移带来的抬头力矩，进而优化会权衡配平阻力和机翼诱导阻力的变化，最终的优化结果就是机翼载荷外移，有效减小机翼的诱导阻力，故可得出对于民用客机构型，通过后移其参考重心位置即放宽其固定静稳定度然后再对机翼进行气动优化设计可有效改善机翼表面压力分布形态和升力系数分布，并实现全机较大程度减阻的结论。

图8 初始构型机翼和平尾沿展向升力系数分布对比Fig.8 Comparison of lift coefficients distributions of wing and tail along span among initial configurations

图9 优化构型机翼剖面压力系数分布对比Fig.9 Comparison of wing section pressure coefficient distributions among optimized configurations

图10 优化构型机翼和平尾沿展向升力系数分布对比Fig.10 Comparison of lift coefficients distributions of wing and tail along span among optimized configurations

图参考重心时初始和优化构型机翼剖面压力系数对比Fig.11 Comparison of wing section pressures coefficients of initial and optimized configurations (15% c.g. position)

图参考重心时初始和优化构型机翼剖面压力系数对比Fig.12 Comparison of wing section pressure coefficients of initial and optimized configurations (20% c.g. position)

图参考重心时初始和优化构型机翼剖面压力系数对比Fig.13 Comparison of wing section pressure coefficients of initial and optimized configurations (25% c.g. position)

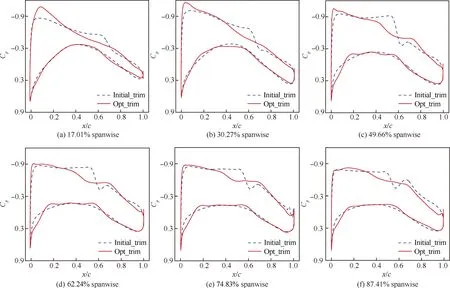
图参考重心时初始和优化构型机翼剖面压力系数对比Fig.14 Comparison of wing section pressure coefficients of initial and optimized configurations (30% c.g. position)

图参考重心时初始和优化构型机翼剖面压力系数对比Fig.15 Comparison of wing section pressure coefficients of initial and optimized configurations (35% c.g.position)

6 结 论

1) 建立了一套基于离散伴随方法的气动梯度优化设计系统，针对CRM机翼-机身-平尾构型进行了不同参考重心位置下的减阻优化设计，设计结果表明配平阻力有效减小，机翼激波强度减弱，表面压力分布形态改善，全机阻力降低，验证了优化系统的可行性。

2) 对于初始构型，仅后移其参考重心位置即放宽固定静稳定度，可通过改变机翼尾翼升力分布从而减小配平阻力来有效实现减阻。

3) 针对不同参考重心位置下考虑全机配平约束的优化设计，所有优化构型均表现出内翼段激波强度明显减弱，外翼段双激波压力分布形态得到改善，明显减弱了第一个激波的强度；而随着重心位置后移，外翼段前缘吸力峰值明显降低以及双激波的强度有效减弱，且机翼的升力系数分布更加贴合最佳升力系数分布，最终综合实现全机阻力的有效减小。

4) 在民用客机的减阻设计中，考虑放宽静稳定度的气动优化设计具有较大的减阻潜力。

[1] LUTZE F H. Trimmed drag considerations[J]. Journal of Aircraft, 1977, 14(6): 544-546.

[2] 许维进， 刘志敏. 重心位置对飞机阻力及其飞行性能的影响[J]. 飞行力学, 1999, 17(1): 54-58.

XU W J, LIU Z M. Effect of center-of-gravity position on aircraft drag and flight performance[J]. Flight Dynamics, 1999, 17(1): 54-58 (in Chinese).

[3] SACHS G. Minimum trimmed drag and optimum c.g. position[J]. Journal of Aircraft, 1978, 15(8): 456-459.

[4] 王子方. 放宽静稳定度对平衡阻力影响计算方法探讨[J]. 飞行力学, 1987, 2(3): 18-22.

WANG Z F. Influence on the trimmed drag calculation method of relaxing static stability[J]. Flight Dynamics, 1987, 2(3): 18-22 (in Chinese).

[5] 周慧钟， 李忠应. 放宽飞行器纵向静稳定度问题的分析研究[J]. 飞航导弹, 1998(2): 8-13.

ZHOU H Z, LI Z Y. Study on relaxing longitudinal static stability of the flying vehicle[J]. Aerodynamic Missile Journal, 1998(2): 8-13 (in Chinese).

[6] 王华友， 李振水, 高亚奎, 等. 某机放宽纵向静稳定度效益分析[J]. 飞行力学, 2007, 25(1): 19-21.

WANG H Y, LI Z S, GAO Y K, et al. Effect analysis on basic flight performance for a RLSS aircraft[J]. Flight Dynamics, 2007, 25(1): 19-21 (in Chinese).

[7] 冯小刚, 李俨, 崔永青. 民机放宽静稳定性的研究[J]. 电子设计工程, 2013, 21(19): 118-122.

FENF X G, LI Y, CUI Y Q. Research on relaxed static stability of civil aircraft[J]. Electronic Design Engineering, 2013, 21(19): 118-122 (in Chinese).

[8] 熊俊涛, 乔志德, 杨旭东, 等. 基于黏性伴随方法的跨声速机翼气动优化设计[J]. 航空学报, 2007, 28(2): 281-285.

XIONG J T, QIAO Z D, YANG X D, et al. Optimum aerodynamic design of transonic wing based on viscous adjoint method[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 281-285 (in Chinese).

[9] LYU Z J, KENWAY G K W, MARTINS J R R A. Aerodynamic shape optimization investigations of the common research model wing benchmark[J]. AIAA Journal, 2015, 53(4): 968-985.

[10] JAMESON A. Optimum aerodynamic design using CFD and control theory: AIAA-1995-1729-CP[R]. Reston, VA: AIAA, 1995.

[11] REUTHER J, JAMESON A, FARMER J, et al. Aerodynamic shape optimization of complex aircraft configurations via an adjoint formulation: AIAA-1996-0094[R]. Reston, VA: AIAA, 1996.

[12] ECONOMON T D, PALACIOS F, COPELAND S R, et al. SU2: An open-source suite for multiphysics simulation and design[J]. Journal of Aircraft, 2016, 54(3): 828-846.

[13] CARRIER G, DESTARAC D, DUMONT A, et al. Gradient-based aerodynamic optimization with the elsA software[C]//Proceedings of 52nd Aerospace Sciences Meeting—AIAA SciTech 2014. Reston， VA: AIAA, 2014.

[14] SCHWAMBORN D, GERHOLD T, HEINRICH R. The DLR TAU-code: Recent applications in research and industry[C]//Proceedings of the European Conference on Computational Fluid Dynamics, 2006.

[15] 陈颂, 白俊强, 史亚云, 等. 民用客机机翼/机身/平尾构型气动外形优化设计[J]. 航空学报, 2015, 36(10): 3195-3207.

CHEN S, BAI J Q, SHI Y Y, et al. Aerodynamics shape optimization design of civil jet wing-body-tail configuration[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3195-3207 (in Chinese).

[16] 左英桃, 傅林, 高正红, 等. 机翼-机身-短舱-挂架外形气动优化设计方法[J]. 航空动力学报, 2013, 28(9): 2009-2015.

ZUO Y T, FU L, GAO Z H, et al. Aerodynamic optimization design of wing-body-nacelle-pylon configuration[J]. Journal of Aerospace Power, 2013, 28(9): 2009-2015 (in Chinese).

[17] 唐智礼. 约束最优控制理论及其在气动优化中的应用[J]. 力学学报, 2007, 39(2): 273-277.

TANG Z L. Constrained optimum control theory: Application to aerodynamic design[J]. Chinese Journal of Theoretical Applied Mechanics, 2007, 39(2): 273-277 (in Chinese).

[18] 徐兆可, 夏健, 高宜胜. 基于三维非结构网格的连续伴随优化方法[J]. 南京航空航天大学学报, 2015, 47(1): 145-152.

XU Z K, XIA J, GAO Y S. Continuous adjoint approach to aerodynamic optimization on 3D unstructured grids[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(1): 145-152 (in Chinese).

[19] 吴文华, 范召林, 陈德华, 等. 基于伴随算子的大飞机气动布局精细优化设计[J]. 空气动力学学报, 2012, 30(6): 719-724.

WU W H, FAN Z L, CHEN D H, et al. Adjoint based on high precise aerodynamic shape optimization for transonic civil aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(6): 719-724 (in Chinese).

[20] 李彬, 邓有奇, 唐静, 等. 基于三维非结构混合网格的离散伴随优化方法[J]. 航空学报, 2014, 35(3): 674-686.

LI B, DENG Y Q, TANG J, et al. Discrete adjoint optimization method for 3D unstructured grid[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 674-686 (in Chinese).

[21] SEDERBERG T W, PARRY S R. Free-form deformation of solid geometric models[J]. Computer Graphics, 1986, 20(4): 151-160.

[22] VASSBERG J C, DEHAAN M A, RIVERS S M, et al. Development of a common research model for applied CFD validation studies: AIAA-2008-6919[R]. Reston, VA: AIAA, 2008.

[23] LEVY D W, LAFLIN K R, TINOCO E N, et al. Summary of data from the fifth computational fluid dynamics drag prediction workshop[J]. Journal of Aircraft, 2014, 51(4): 1194-1213.

[24] SAAD Y, SCHULTZ M H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(3): 856-869.

[25] NOCEDAL J, WRIGHT S J. Numerical optimization[M]. New York: Springer, 1999: 526-572.

(责任编辑： 李明敏)

*Corresponding author. E-mail: junqiang@nwpu.edu.cn

Aerodynamic optimization design for civil aircraft considering relaxed static stability

LI Li1, BAI Junqiang1,*, GUO Tongbiao1, CHEN Song2

1.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.HubeiSpaceVehicleResearchInstitute,Wuhan430040,China

The study on the aerodynamic optimization design of the civil jet wing-body-tail configuration with different static stability is presented, which intends to efficiently reduce the aircraft’s total drag considering trimming. It is obtained that considering static stability in drag-reduction design can have great potential of reducing the drag. The Free-Form Deform (FFD) technique is adopted to parameterize the wing shape for aerodynamic optimization design and rotate horizontal tail for trimming the pitching moment of the whole aircraft. The discrete adjoint technique based on Reynolds Averaged Navier-Stokes (RANS) equations is used to solve the gradients of targets with regard to design variables, and sequential quadratic programming is used to conduct the gradient-based optimization design. Based on the Common Research Model (CRM), optimizations considering trimming constraint with different c.g. positions are carried out to reduce aerodynamic drag, and feasibility of the optimization system is confirmed. The results of optimization cases show that when the c.g. position moves backward, the optimization configuration has smaller trim drag, obviously lower negative pressure peak of the leading edge in the outer wing, and weaker shock wave. The distribution of wing spanwise lift coefficient is improved to achieve the optimized design result.

relaxed static stability; discrete adjoint; aerodynamic optimization design; trim drag; lift coefficient distribution

2017-01-07； Revised： 2017-01-19； Accepted： 2017-02-16； Published online： 2017-02-22 19:21

URL： www.cnki.net/kcms/detail/11.1929.V.20170222.1921.002.html

National Basic Research Program of China (2014CB744804)

V211.41+1

A

1000-6893(2017)09-121112-14

2017-01-07； 退修日期： 2017-01-19； 录用日期： 2017-02-16； 网络出版时间： 2017-02-22 19:21

www.cnki.net/kcms/detail/11.1929.V.20170222.1921.002.html

国家“973”计划(2014CB744804)

*通讯作者.E-mail: junqiang@nwpu.edu.cn

李立， 白俊强， 郭同彪， 等. 考虑放宽静稳定度的民用客机气动优化设计[J]. 航空学报， 2017, 38(9): 121112. LI L, BAI J Q, GUO T B, et al. Aerodynamic optimization design for civil aircraft considering relaxed static stability[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 121112.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121112