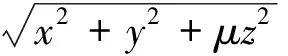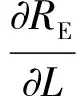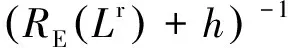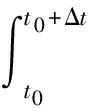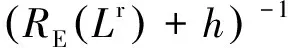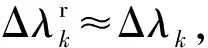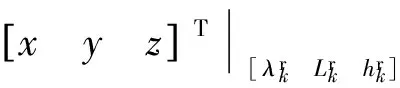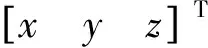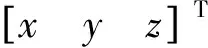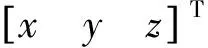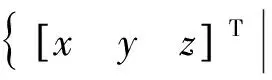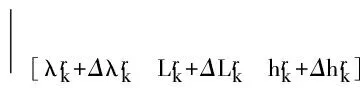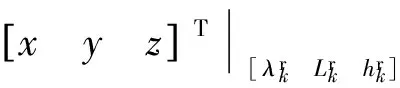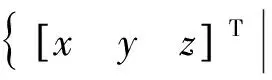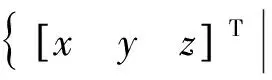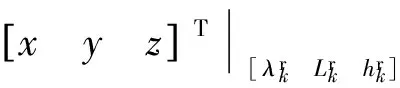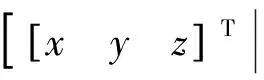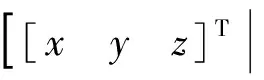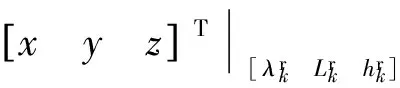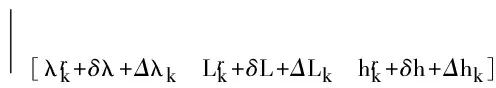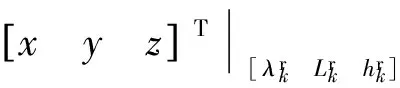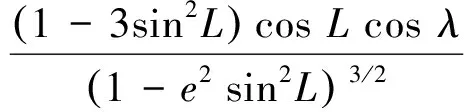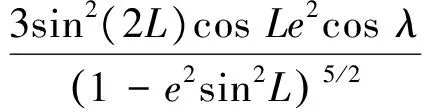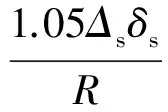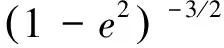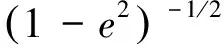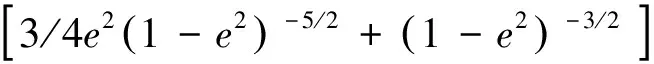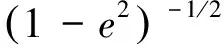一种基于相对位置约束的双星定位方法
2017-11-20李正张海王伟扬
李正, 张海, 王伟扬
北京航空航天大学 自动化科学与电气工程学院, 北京 100083
一种基于相对位置约束的双星定位方法
李正, 张海*, 王伟扬
北京航空航天大学 自动化科学与电气工程学院, 北京 100083
全球卫星定位系统(GNSS)需要至少4颗卫星才能提供持续、准确的定位结果。在有障碍物遮挡的城市街道、山谷或者存在压制式干扰的战场环境中,往往会出现可见星数量降低至4颗以下的情况。针对只有2颗可见星的定位问题,提出了通过相对位置变化对绝对位置进行解算的定位模型,证明了该模型的可行性,并研究了该模型的数值计算方法和几何搜索方法。仿真实验和实际跑车试验表明,在只有2颗可见星条件下,该方法的定位精度明显优于传统的INS/GNSS紧组合算法,并且对初始位置的精度不具有依赖性。
全球卫星定位系统; 两颗可见星; 定位; 相对位置约束; 组合导航
全球卫星定位系统(GNSS)在组合导航[1]、智能交通[2]、大地测量[3]、精密单点定位[4-5]等领域有广泛的应用。传统的GNSS定位算法需要4颗可见星才能有效定位[6]。但在城市街区、隧道、山谷以及压制式干扰等困难环境中,上述条件通常不易满足[7]。当只有3颗可见星时,通过接收机的海拔高度辅助,以及惯性导航系统(INS)与GNSS组合Kalman滤波的方法能够获得较好的定位结果[8]。但可见星只有2颗时,传统的组合导航滤波器观测信息不足,滤波结果将随惯导累积误差迅速发散[9-10]。
针对2颗星定位问题,文献[11]提出了一种城市内移动车辆的定位算法,该算法在前一时刻位置已知的前提下,通过测量两个时刻车辆的直线距离,对当前时刻的位置进行解算。该算法虽然精度较高,但由于是递推算法,所以对初始位置有较高的精度要求,且车辆在运动过程中不能有明显的高度变化[11]。文献[12]通过研究高精度铷原子钟的误差模型,在可见星不足的情况下对接收机钟差进行预测,同时结合高度信息解决2颗星的定位问题。文献[13-14]提出了在弱信号情况下,通过改进数值计算方法,实现只有2颗可见星的定位方法。但是该方法只能解决单点定位问题,对于运动载体,无法满足实时性要求。文献[15-16]等通过设计新的自适应滤波方法,降低只有2颗可见星时的定位误差,但是在定位原理上仍没有突破性进展。
针对以上算法存在的不足,本文提出了根据相对位置变化对载体的绝对位置进行解算的方法。该方法对载体的运动模式没有约束,不依赖于初始位置精度,且定位误差没有累积效应。文章的主要内容包含4个方面:首先对基于相对位置约束的两颗星定位模型进行介绍;第二,对算法的可行性进行了理论分析;第三,给出了定位结果的两种数值解法;最后通过仿真实验,验证算法的有效性和定位精度。
1 定位原理
1.1 基本思想
卫星接收机获得的伪距信息在地心地固(ECEF)坐标系下一般表述为[17]
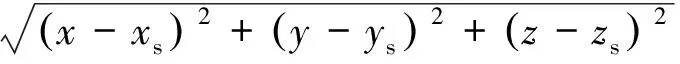
(1)
式中:[xyz]T为接收机的位置;[xsyszs]T为卫星位置;δtu为接收机的钟差。接收机位于以卫星为球心半径为ρ-δtu的球面上。当有2颗可见星时,如图1所示,两球面相交于一空间圆,该圆为接收机位置的可行解轨道。
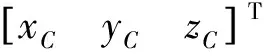
(2)
由此可推知,在相隔Δt的tk与tk+1两个时间点上,可以确定如图2所示的两个轨道平面。
本文的核心思想在于:如果接收机在Δt时间内的位置变化矢量rk已知,利用rk的起点、终点应分别位于两个可行解轨道上的约束,使用多个时刻间的位置变化矢量测量,能够实现对载体位置的有效估计。
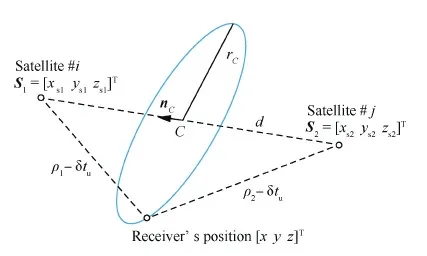
图1 由2颗可见星确定的可行解 Fig.1 Feasible solution by two visible satellites
图2 2颗可见星定位的原理图 Fig.2 Principle diagram of positioning algorithm with two visible satellites
1.2 数学模型
(3)
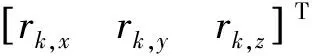
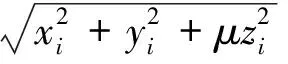
(4)
式中:Re为地球长半轴;μ为一个与高度测量值相关的因子,其含义与推导过程详见附录A。
非线性方程组可记为
FX=b
(5)
式中:X=[x1y1z1δtu1x2y2z2δtu2]T为被估计状态;b=[ρ11ρ11h1ρ11ρ11h2rk,xrk,yrk,z]T为测量值。考虑测量值存在噪声,记b对应的噪声标准差为
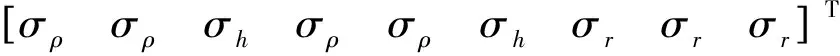
(6)
式中:下标ρ、h、r分别表示伪距、高度和位置变化。
采用加权的思想[18],式(3)可进一步转化为如下最优化问题:
(7)
2 最优解的计算方法
根据本文提出的2颗星定位原理,针对不同情况,采用两种最优解的计算方法。一是基本的数值解法,二是结合几何含义的搜索方法。
2.1 数值计算方法
Gauss-Newton迭代算法是解决式(7)所示的最优化问题的基本方法,其迭代公式为
(8)
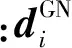
(9)
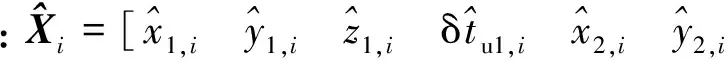
rm1=
rm2=
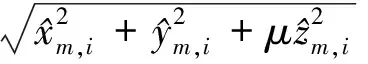
定位过程中,迭代初值通常选择上一时刻的估计值。
2.2 几何搜索方法

2.2.1 搜索原理
短时间内接收机的钟漂可近似为0,即式(3)中δtu1=δtu2。当钟差为固定值δtu时,可确定图1 所示的轨道圆,记为Tk。根据高度限制,可将接收机的大致范围Ls在Tk上标记出来,如图3 所示。轨道圆半径极大,在局部区域近似为一条直线。
将rk的终点P在可行解区域Ls上滑动,PL和PH分别为可行解区的左右端点,其起始点D到tk-1时刻的轨道圆Tk-1的最短距离为Δ1。因单一位置变化矢量不能消除钟差模糊度,进而无法实现位置的准确求解,本文采用多时刻位置变化矢量约束的方式提高精度。
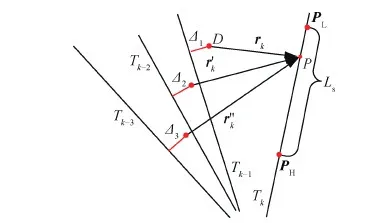
图3 几何搜索方法 Fig.3 Searching method by geometric relationships
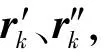
搜索最优解δtu,P,使得最优解对应的如下代价函数最小:
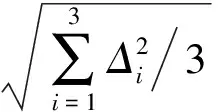
(10)
图4为Δi的计算方法:Tk-i为轨道圆,C为圆心,D点为位置变化矢量的起始点,D′为D点在圆轨道平面的投影,则D点到轨道圆的最短距离为DE。
由于C点和D点坐标可求,法向量nC由式(2)给出,故夹角θ可求。由几何关系可得
(11)
式中:|CD|为C点到D点的线段长度。
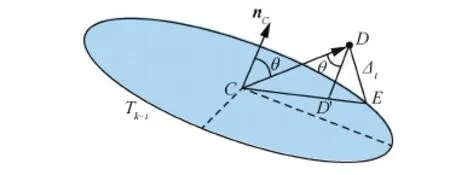
图4 空间点D到轨道圆的最短距离 Fig.4 Minimum distance between point D and the orbit
2.2.2 基于黄金分割的搜索策略
钟差的搜索区间[δtuL,δtuH]可通过经验设置,也可以借鉴文献[12]提供的时钟模型进行预测。滑动区间Ls则由高度h的取值范围决定。一般情况下,将高度传感器的测量误差视为标准差为σh的零均值白噪声。利用3σ准则,确定高度的取值范围为
h∈hL,hH=hm-3σh,hm+3σh
(12)
式中:hm为测量值。根据式(12)可分别求出hL和hH对应的数值解:
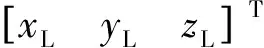
(13)
由于轨道圆半径rC极大,可认为最优点位于PL和PH的连线上。但通过遍历PLPH线段上每一个采样点寻找最优解的方法计算量极大。本文采用黄金分割搜索的方法查找最优解。
设第q次搜索区间为aq,bq,计算区间内的两个试探点,uq,vq∈aq,bq:
(14)
式中:σ=0.618,计算两个试探点对应的代价函数ΓΔ(uq)和ΓΔ(vq),并比较二者大小。如果ΓΔ(uq)≤ΓΔvq,则说明最优解在aq,vq范围内,即
(15)
由于黄金分割点的特殊性,uq变为新区间的黄金分割点,即vq+1=uq,所以对于区间aq+1,bq+1只需要计算新的uq+1即可。同理,如果ΓΔuq>ΓΔvq,则
(16)
反复搜索,直到区间长度小于某阈值ε。
用同样的搜索原理对钟差进行搜索,即可获得最终解。虽然嵌套两层搜索,但是由于钟漂的稳定性,可根据上一时刻的搜索结果对下一时刻的钟差取值范围进行有效约束,从而减少搜索次数。
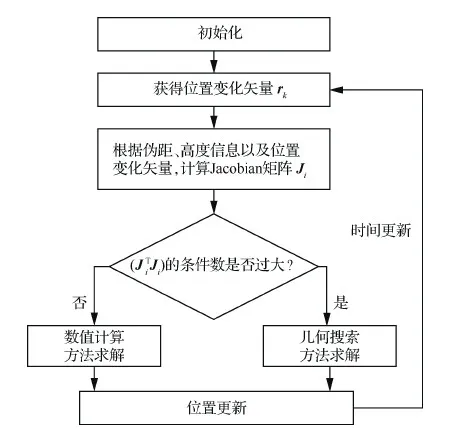
图5 本文所提方法流程图 Fig.5 Flow chart of proposed method
3 对位置变化矢量rk的理论分析
由图5可知,本文的定位原理依赖于对伪距、高度和位置变化矢量rk的有效测量。伪距和高度信息可由接收机和高度传感器直接获得,但rk则无法直接测量。一般情况下,需要通过对速度进行积分获得。需要指出的是,虽然当速度可测时,可以通过积分计算位置,但积分过程有误差累计效应,如果tk时刻的位置不准确,tk+1时刻的位置也会随之发散。此时传统的积分算法,比如惯导,并不能实现自校正。本节主要证明,即便tk时刻的位置有很大误差,rk也能获得较高精度的测量,进而确保本文的算法能够正常执行,最终将定位精度收敛到合理范围,防止进一步发散。
3.1 rk的基本计算方法
rk的3个分量是在ECEF坐标系下的坐标,需要通过对地速进行积分,获得运动载体地理位置(经度λ、纬度L、高度h)的变化,再将地理位置的变化转化为ECEF坐标的变化。载体在运动过程中,经度、纬度、高度的计算公式为[19]
(17)
式中:λk、Lk、hk分别为tk时刻接收机的经度、纬度、高度;VE、VN、VU分别为载体的东-北-天三向速度;RN、RE分别为子午面曲率半径和横向曲率半径,其计算公式为[20]
(18)
式中:e为地球的偏心率;Re为地球长半轴,地理位置向ECEF坐标系的转换公式为[21]
(19)
则
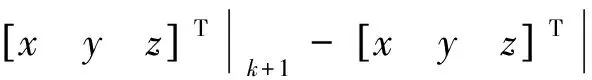
(20)
3.2 初始位置未知时rk的计算方法
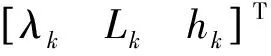
(21)
根据3颗星定位原理[17],可用牛顿迭代法计算出精度较高的数值解。同时注意到,μ的取值与1近似,且μ=1时式(21)可变形为首一多项式,存在解析解。可将μ=1时的解析解作为牛顿迭代的初值,迭代多次获得准确的数值解。
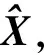
GΔX=ν
(22)
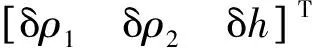
(23)
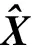
(24)
ΔX=G-1ν
(25)
定位误差为
(26)
记
(27)
其中:pij为ei与ej的内积,表达式为
(28)
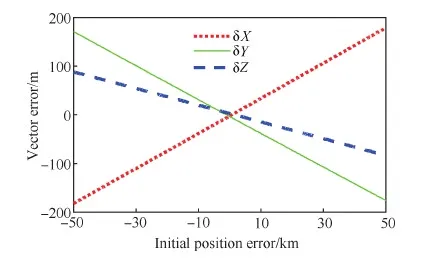
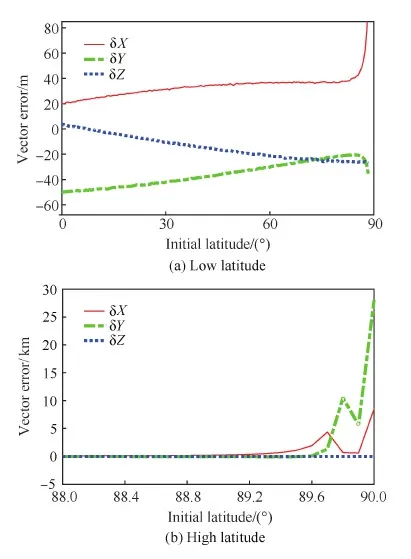
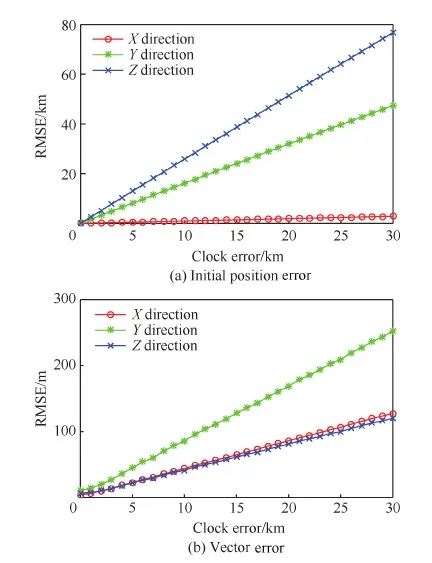
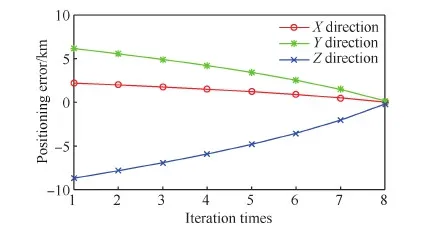
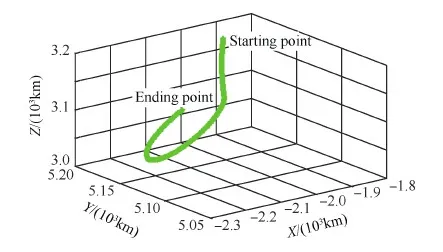
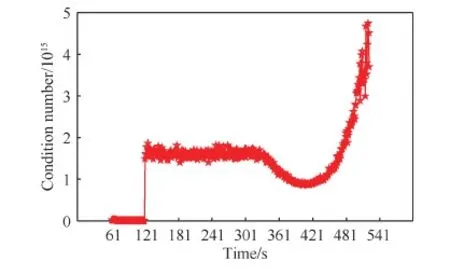
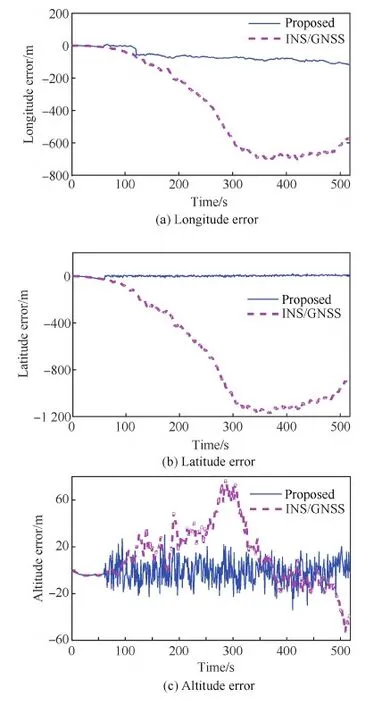
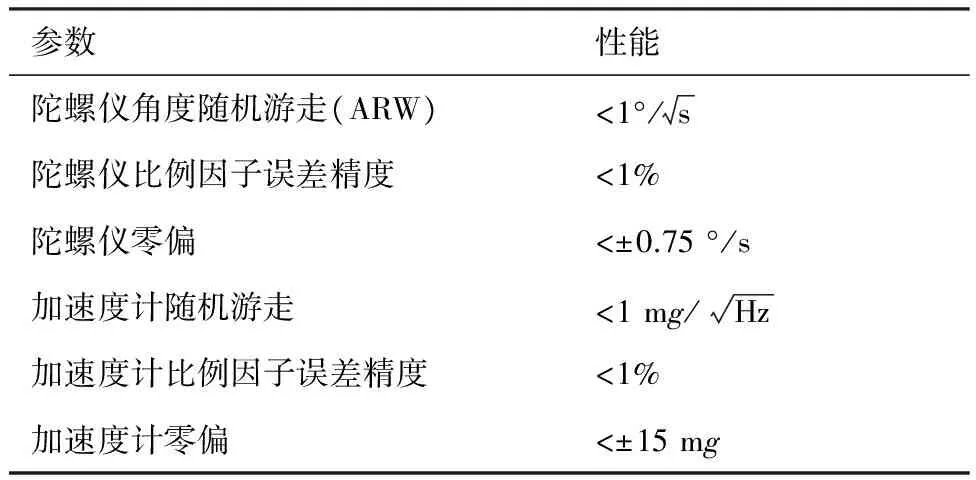
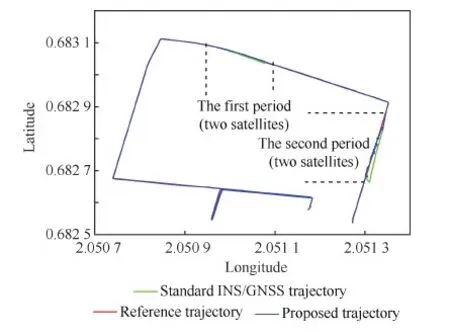
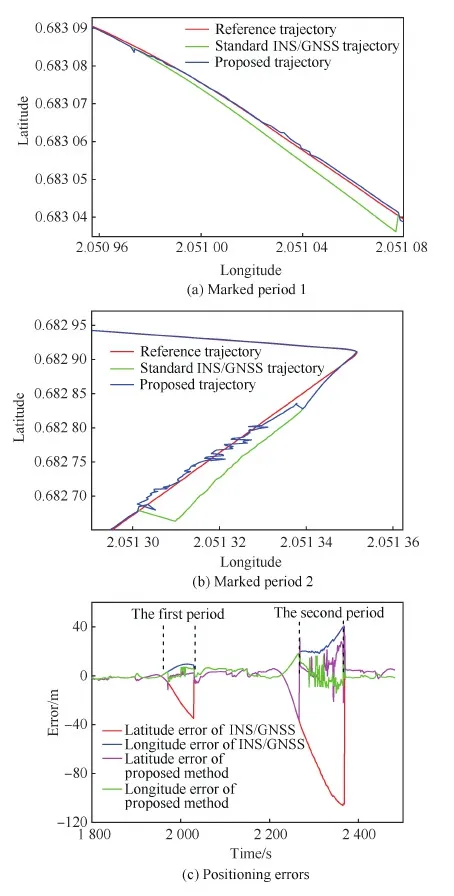
因μ>1(见附录A),所以1 (29) 从而有 (30) (31) 文献[22]指出,对于典型的天线,信号增益随信号入射角的增大而降低。在有遮挡的环境下,信号入射角一般小于60°。从而限定e1、e2与e3的夹角大于120°,进而有 -1≤p13,p23≤-0.5 (32) 而e1与e2的夹角过小时会导致2颗星可辨性差,通常大于15°,结合天线增益的角度限制,易知 -0.5≤p12≤0.966 (33) 根据p13、p23、p33以及p12的取值范围,可得 (34) 若钟差为1 000 m,高度测量误差为10 m,则 (35) 由线性代数的相关知识知,G为以e1、e2和e3为棱的平行六面体的体积,当体积的数量级为100~10-1时,对应的误差上限为2~20 km。可见由式(21)计算的初始位置,在G较小的情况下将包含较大误差。但由此计算的rk和最终的定位结果仍可以获得较好的精度,4.2节对此进行了实例验证。 3.3 位置变化矢量rk的精度分析 假设1载体的运动范围为中低纬度地区,即南北纬60° 范围内。 假设2Δtk时间内,载体的海拔高度、航向、速度等可测,高度测量的噪声方差最大为200 m2,在航向误差与速度误差的综合作用下,东-北-天三向速度有10-1m/s数量级的稳态误差。 在以上假设下,本文给出两个便于工程应用的定性结论,并在附录B和附录C中进行详细证明。 结论1Δtk时间内,经度、纬度、高度的变化在数值上与真值近似,即 (36) 以上分析的是rk的计算精度,其对定位结果的影响较为复杂。但通过大量实验可以验证,当tk时刻与tk+1时刻发生换星时,本文定位误差远小于rk的计算误差;如果没有换星,定位误差较大,但仍小于rk的计算误差。 本文首先通过仿真实验,对提出的方法进行原理性验证,然后通过实际跑车实验进一步证明其正确性和有效性。 4.1 仿真实验 仿真实验由3部分组成,首先验证位置变化矢量rk的精度,其次通过实例验证无先验知识的rk计算方法的有效性,最后通过与标准的INS/GNSS紧组合算法作对比,验证定位方法的有效性。 4.1.1 位置变化矢量与初始位置误差的关系 实验1飞行器的真实起点为北纬40°,东经116°,高度恒为10 000 m,速度大小恒为400 m/s,航向为北偏东45°,如此飞行60 s,计算对应的位置变化矢量。测速系统存在0.1 m/s的稳态误差,测速噪声的标准差为2 m/s,航向测量噪声的标准差为0.5°,高度测量噪声的标准差为20 m,采样频率为10 Hz。 假设参与计算的起点的经度、纬度同时有Δs的误差,Δs的取值范围为[-50,50] km。用蒙特卡罗法仿真1 000次,计算误差的均值,结果如图6 所示。从图中可以看出,位置变化矢量具有将初始位置的大误差缩小的功能。尤其是在导航过程中,定位误差一般都在10 km范围内,对应的位置变化矢量误差很小,完全能够满足2颗星的定位要求。 实验2与实验1同样的运动方式,飞行器真实起点的经度不变,纬度从北纬1°遍历到北纬90°,参与计算的起点的经度、纬度有固定的10 km 误差,观察这固定的10 km误差在不同纬度造成的位置变化矢量的误差。用蒙特卡罗法仿真1 000次,计算误差的均值。图7(a)反映了低纬度地区的误差情况。图7(b)反映了高纬度地区的情况,可以看出,在极地附近,位置变化矢量误差急速增加。其主要原因在于:根据附录B中的式(B1)和式(B2),误差在经度方向上的分量与纬度的正割值成正比。在极地附近,纬度的正割趋于无穷大,所以经度变化的误差极大,反映在位置变化矢量上,即3个轴的误差分量很大。由此也可以发现,本文提供的方法,在极地附近可行性较差。 图6 位置变化矢量误差与初始位置误差的关系 Fig.6 Vector error derived from initial position error 图7 固定的初始位置误差导致的位置变化矢量误差 Fig.7 Vector error derived from a fixed initial position error 4.1.2 初始位置未知时rk的计算方法验证 本文3.2节中提到,初始位置未知时,忽略接收机钟差,可对初始位置进行近似计算。此处给出一个计算范例。 tk时刻,卫星1与卫星2的空间位置分别为(9 316 492,16 106 224,18 954 148)、(-14 639 082,14 650 041,16 629 515),对应的伪距分别为22 230 740.0、20 819 416.7,tk+1时刻,卫星1与卫星2的空间位置分别为(9 315 716,16 108 506,18 952 588)、(-14 641 190,14 650 256,16 627 468),对应的伪距分别为22 233 593.8,20 807 742.9;tk与tk+1间隔60 s。飞行器初始地理位置为(30°,110°,1 000 m),飞行过程中高度不变,东向与北向速度恒为300 m/s。高度测量噪声的标准差为20 m,测速系统存在0.1 m/s的稳态误差,测速噪声的标准差为2 m/s。钟差的取值范围为[0,30] km,以1 000 m为采样间隔。对每一个采样点用蒙特卡罗法计算1 000次位置变化矢量,并与真实的位置变化矢量做差,计算3个分量上的均方根误差。 结果如图8(a)和图8(b)所示。其中图8(a)为在不同钟差情况下通过式(21)计算的初始位置的均方根误差(RMSE)。从图中可以看出,初始位置误差随钟差的增加而增大,且数值较大,单位为km。图8(b)为在图8(a)的初始位置误差基础上,对位置变化矢量进行计算的误差结果。从图中可以看出,虽然位置变化矢量误差也随钟差的增加而增大,但是单位为m,明显小于初始位置误差。该试验表明,2.2节中对没有先验知识的位置变化矢量的计算方法是有效的。 图8 不同钟差导致的位置变化矢量的均方根误差以及相应的位置变化矢量的误差 Fig.8 RMSE of initial position error and vector error derived from different clock error 取钟差5 000 m的情况,用本文提出的2颗星定位算法,求取接收机位置。由于此时误差很大,需要反复迭代,不断更新初始位置,进而逐渐提高定位精度。图9为迭代8次过程中的定位误差,从图中可以看出,定位方法具有一定的收敛性。 图9 定位误差与求解次数 Fig.9 Converging positioning error and iteration times 4.1.3 与紧组合的对比实验 与标准的紧组合算法进行对比,飞行器的运动轨迹及传感器数据由轨迹发生器生成,运动轨迹如图10所示。 惯导系统中,陀螺的零偏为1 (°)/h,随机噪声为20 (°)/h,加速度计零偏为1 mg,随机噪声为20 mg,人为设置可观测星的数量始终为2。对于本文提出的2颗星定位方法,直接用紧组合的速度输出作为辅助测速系统,从而计算出位置变化矢量,位置变化矢量的计算时间间隔为60 s。即飞行器飞行60 s以后开始进行解算,前60 s用紧组合的结果代替。 图10 飞行器运动轨迹 Fig.10 Trajectory of aircraft 根据条件数的变化,本文在条件数较小时直接采用数值解法,当条件数跳变时采用几何搜索方法。最终的定位误差如图12所示。 图11 条件数 Fig.11 Condition number 图12 定位误差 Fig.12 Positioning error 4.2 跑车试验 为了进一步证明本文所提出方法的正确性和有效性,课题组进行了实际跑车试验。 4.2.1 试验条件 试验采用的硬件平台为北京航空航天大学和航天恒星科技有限公司联合研制的ISS/GNSS紧组合原理样机。其中接收机为载波相位双频差分接收机,其单点定位误差为5 m,速度误差为0.1 m/s。惯性器件选用美国Crossbow公司生产的IMU440,其主要性能指标如表1 所示。气压计设备选用的是MEAS公司生产的数字压力传感器MS5803-02BA,该款气压计的分辨率高达10 cm、体积小(6.2 mm×6.4 mm)、稳定性高。同时,选用精度更高的组合导航系统IMU-ISA-100C计算跑车试验的参照值,该系统由NovAtel公司研制,其定位精度可达厘米级。 表1 IMU440 主要性能Table 1 Performance of IMU440 为了实现可见星不足4颗的试验条件,跑车环境选在建筑物较多的街区。此外,当可见星有3颗时,将信噪比最低的一颗剔除,进而对本文方法进行更有针对性的验证。 4.2.2 试验结果 跑车试验在天津进行,将IMU-ISA-100C系统的输出作为标准值进行对比,行车轨迹如图13所示。当可见星足够多时,用传统的紧组合算法结果作为输出;当可见星只有2颗时,切换到本文算法。 跑车试验持续2 500 s,在[1 944,2 030] s区间段(对应图13中的时间段1)和[2 217,2 369] s区间段(对应图13中的时间段2),接收机受建筑物遮挡,可见星数量较少,大部分少于4颗。为了对本文算法进行充分验证,强制将这两个时间段的可见星数量设置为2。此外,计算位置矢量的时间设置为30 s,跑车刚进入这两个时间段时,前30 s仍采用标准的紧组合算法,之后切换到本文方法。 图13 跑车轨迹 Fig.13 Vehicle trajectory 图14为2颗星下本文方法与标准紧组合算法的对比结果,其中图14(a)、图14(b)分别为时间段1和时间段2的轨迹,图14(c)为经纬度误差。从图中可以看出:本文方法计算的轨迹更接近标准轨迹;本文方法的定位误差误差整体上要小于传统算法,虽波动性较强,但没有明显的误差累计效应。 图14 对比结果 Fig.14 Comparison results 本文根据相对位置的约束关系,提出了一种新的双星定位方法。该方法通过测量接收机在空间中的相对位置变化矢量,在高度信息辅助下实现仅有2颗可见星环境下的较高精度定位。该方法的主要特点包括: 1) 对运动载体的运动形式没有要求,既可以测量高速运动的飞行器,也可以进行单点测量,应用较为广泛。 2) 误差没有累积效应,适合与惯导等其他定位系统进行组合。 3) 不需要初始位置对准,具有较强的灵活性。 4) 只有两颗低轨道通信卫星,在能获得伪距和卫星位置的前提下也能实现定位,具有较好的扩展性。 [1] 刘百奇, 房建成. 一种基于可观测度分析的SINS/GPS自适应反馈校正滤波新方法[J]. 航空学报, 2008, 29(2): 430-436. LIU B Q, FANG J C. A new adaptive feedback Kalman filter based on observability analysis for SINS/GPS[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 430-436 (in Chinese). [2] CHEN W, LI X, SONG X, et al. A novel fusion methodology to bridge GPS outages for land vehicle positioning[J]. Measurement Science and Technology, 2015, 26(7): 075001. [3] 程鹏飞, 文汉江, 孙罗庆, 等. 中国大陆 GPS 速度场的球面小波模型及多尺度特征分析[J]. 测绘学报, 2015, 44(10): 1063-1070. CHENG P F, WEN H J, SUN L Q, et al. The spherical wavelet model and multiscale analysis of characteristics of GPS velocity fields in mainl and china[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1063-1070 (in Chinese). [4] 刘经南, 叶世榕. GPS非差相位精密单点定位技术探讨[J]. 武汉大学学报: 信息科学版, 2002, 27(3): 234-240. LIU J N, YE S R. GPS precise point positioning using undifferenced phase observation[J]. Geomatics and Information Science of Wuhan University, 2002, 27(3): 234-240 (in Chinese). [5] PAN S, CHEN W, JIN X, et al. Real-time PPP based on the coupling estimation of clock bias and orbit error with broadcast ephemeris[J]. Sensors, 2015, 15(7): 17808-17826. [6] CORPORATION A. NAVSTAR GPS space segment/navigation user interfaces[J]. European Journal of Theology, 1991, 24(5): 272. [7] NOURELDIN A, KARAMAT T B, GEORGY J. Fundamentals of inertial navigation, satellite-based positioning and their integration[M]. Berlin: Springer Science & Business Media, 2012. [10] CHEN L, FANG J. A hybrid prediction method for bridging GPS outages in high-precision POS application[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(6): 1656-1665. [11] HATANO H, KITANI T, FUJII M, et al. Positioning method by two GNSS satellites and distance sensor in urban area[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2015, 98(1): 275-283. [12] YEN S W, VAN GRAAS F, DE HAAG M U. Positioning with two satellites and known receiver clock, barometric pressure and radar elevation[J]. GPS Solutions, 2015, 101(12): 1-15. [13] LI J Z. Two satellites positioning algorithm based on AGPS system with two clock bias[C]//2010 2nd International Conference on Computer Engineering and Technology (ICCET), 2010, 2: V2-416-V2-419. [14] 李吉忠, 武穆清, 李筱叶. 利用Marquardt算法进行两颗卫星的AGPS定位[J]. 北京邮电大学学报, 2009, 32(2): 39-42. LI J Z, WU M Q, LI X Y. Two satellites positioning method of AGPS with Marquardt algorithm[J]. Journal of Beijing University of Posts & Telecommunications, 2009, 32(2): 39-41. [15] ZHOU Q, ZHANG H, LI Y, et al. An adaptive low-cost GNSS/MEMS-IMU tightly-coupled integration system with aiding measurement in a GNSS signal-challenged environment[J]. Sensors, 2015, 15(9): 23953-23982. [16] ZHANG B Q, CHU H R, SUN T, et al. Error prediction for SINS/GPS after GPS outage based on hybrid KF-UKF[J]. Mathematical Problems in Engineering, 2015(4):1-9. [17] 孙健. GPS和高精度气压高度表的组合导航定位技术研究[D]. 南京: 南京航空航天大学, 2008. SUN J. Research on GPS and high precision baro-altimeter integrated navigation and positioning technology[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008 (in Chinese). [18] SIMON D. Optimal state estimation: Kalman, H infinity, and nonlinear approaches[M]. New York: John Wiley & Sons, 2006: 82. [19] ROBERT M R. Applied mathematics in integrated navigation systems[M]. 3rd ed. Reston: AIAA, 2007: 75. [20] DAVID H T, JOHN L W. 捷联惯性导航技术[M]. 张天光, 王秀萍, 王丽霞, 等译. 北京: 国防工业出版社, 2007: 34. DAVID H T, JOHN L W. Strapdown inertia navigation technology[M]. ZHANG T G, WANG X P, WANG L X, et al. translated. Beijing: National Defense Industry Press, 2007: 34 (in Chinese). [21] 谢刚. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 108. XIE G. Principles of GPS and receiver designs[M]. Beijing: Publishing House of Electronics Industry, 2009: 108 (in Chinese). [22] PAUL D G. GNSS与惯性及多传感器组合导航系统原理[M]. 李涛, 练军想, 曹聚亮, 等译. 北京: 国防工业出版社, 2011: 185. PAUL D G. Principles of GNSS, inertia and multisenso integrated navigation systems[M]. LI T, LIAN J X, CAO J L, et al., translated. Beijing: National Defense Industry Press, 2011: 185 (in Chinese). 附录A 当接收机的海拔高度确定以后,其位置满足式(A1)所示的椭球面方程[18]: (A1) 式中:Re和Rp分别表示地球的长半轴与短半轴。对式(A1)变形为 (A2) 设传感器测量的海拔高度为hc,则 (A3) 显然 h-hc≪Re+hc,h-hc≪Rp+hc (A4) 所以 (A5) 故式(A2)可写为 (A6) (A7) 附录B 将地球的长半轴Re简记为R。设初始位置误差为δs(单位为m),其导致的最大的经度和纬度误差分别为 (B1) 因δs≪RE+h,δs≪RN+h,所以δL为小量。secL为关于纬度的单调递增函数,在本文3.3节中的假设条件下,secL≤2,所以δλ亦为小量。由式(17)可知,经、纬度的变化方程为 (B2) 式中:δVE、δVN为东向速度与北向速度的测量误差。同时,求中RE、RN对L的导数为 (B3) 1) 经度计算通道 式(B2)中Δλk计算通道的被积函数可写为 (B4) 将其按照a/x+δx的形式进行Taylor展开,可得 Iλ≈ (B5) 式中: (B6) 代入式(B3),并进行整理,易知 Iλ≈ (B7) 而 secLr+δL≈secLr+tanLr·secLr·δL (B8) 将式(B7)、式(B8)代入式(B2)中的经度计算通道: (B9) 展开可得 Δλk≈ (B10) 由式(B10)可知,经度变化误差由两部分组成,一是速度测量误差导致的误差项,二是初始位置误差导致的误差项。其中,速度误差满足假设2 条件,所以 (B11) 此外,δL为小量,且载体的运动范围在中低纬度地区,故 VE+δVEtanLr·secLr·δL≪VEsecLr (B12) 所以初始位置误差导致的误差项满足: (B13) 2) 纬度和高度计算通道 式(B2)中纬度计算通道的被积函数与式(B4)类似,即 (B14) (B15) 此外,由于高度通道不参与积分计算,直接通过气压高度表等传感器进行测量,所以也满足: (B16) 附录C (C1) (C2) (C3) 考虑初始位置与真值的关系: 进而有 (C4) 1) δr的x分量 (C5) 而 (C6) (C7) (C8) 故 cosLcosλ·Δh·δh (C9) 式(C9)可简写为 (C10) eλ项: Δλ·δλ≈-R+hcosLsinλ· (C11) 式中:δs为初始位置误差,假设在10 km范围内;Δλ表示运动载体在短时间内的经度变化,通常也在10 km范围内,所以 (C12) 当h为0时,误差最大,故有 (C13) eL项: (C14) 所以 (C15) 式中: (C16) 其中: (C17) 所以: (C18) 进而: ΔL·δL (C19) 飞行器的飞行高度通常在100 km以内,所以 h<100 km≤0.016R (C20) 同时有 (C21) 所以 (C22) 根据式(C19)~式(C22)计算的各变量取值范围,可得 (C23) 式中:Δs为Δt时间内载体在纬度方向上的变化,一般满足Δs<10 km,δs为初始误差在纬度方向上的大小,本文假设在10 km范围内,则 (C24) 此外,高精度的高度传感器,其测量噪声的方差可达200 m2,所以 (C25) 2) δr的y分量 结果同δr的x分量。 3) δr的z分量 分析方法同δr的x分量,这里给出主要分析过程。 (C26) eL项: (C27) 其中: (C28) (C29) (C30) 而 (C31) (C32) (C33) 所以 1.010 3R+h<1.017R+h (C34) 即 eL<1.017R+h·ΔL·δL (C35) 结果同式(C19)。 而高精度的高度传感器,其测量噪声的方差在200 m2以内,所以 (C36) 综上所述,位置变化矢量的误差可控制在300 m范围内。 (责任编辑: 苏磊) URL:www.cnki.net/kcms/detail/11.1929.V.20170213.1146.002.html Apositioningmethodwithtwosatellitesbyrelativepositionconstraint LIZheng,ZHANGHai*,WANGWeiyang SchoolofAutomationScienceandEngineering,BeihangUniversity,Beijing100083,China Theglobalnavigationsatellitessystem(GNSS)needsatleastfourvisiblesatellitestoprovideaccurateandcontinuouspositingresult.However,underharshconditionssuchasurbancanyon,tunnelsandotherspecialenvironments,thenumberofvisiblesatellitesusuallybecomeslessthanfour,whichleadstodegradationofpositioningprecisionorinfeasibilityofthepositioningalgorithm.Thispaperpresentsanovelmethodtoprovidereliablepositionsolutionwithonlytwovisiblesatellites.TherelativepositionchangeduringashortperiodisutilizedasaconstrainconditiontoestimatetheabsolutepositionofGNSSreceiverinthispaper.Thefeasibilityoftheproposedmethodisproved.Thenumericalalgorithmandgeometricalsearchingalgorithmareproposedrespectively.Thesimulationexperimenthasbeencarriedoutandtheresultdemonstratesthattheproposedmethodiseffectiveinimprovingthepositioningperformance.TheproposedmethodhasbetterperformancethantheconventionalINS/GNSScoupledmethodandthepositioningresultsdonotrelyontheinitialposition’sprecision. GNSS;twovisiblesatellites;positioning;relativepositionconstraint;integratednavigation 2016-06-07;Revised2016-11-09;Accepted2017-01-09;Publishedonline2017-02-131146 .E-mailzhanghai@buaa.edu.cn 2016-06-07;退修日期2016-11-09;录用日期2017-01-08; < class="emphasis_bold">网络出版时间 时间:2017-02-131146 www.cnki.net/kcms/detail/11.1929.V.20170213.1146.002.html .E-mailzhanghai@buaa.edu.cn 李正, 张海, 王伟扬. 一种基于相对位置约束的双星定位方法J. 航空学报,2017,38(5):320503.LIZ,ZHANGH,WANGWY.ApositioningmethodwithtwosatellitesbyrelativepositionconstraintJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):320503. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2017.320503 V241.62+5 A 1000-6893(2017)05-320503-15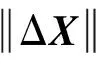
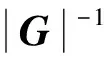

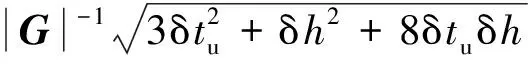
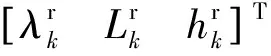
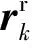
4 实验验证
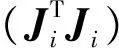
5 结 论