基于一种新的均匀化实施方法的FRP刚度预测

高涛， 漆文凯,2， 沈承,2,*

1.南京航空航天大学 能源与动力学院， 南京 210016 2.江苏省航空动力系统重点实验室， 南京 210016

基于一种新的均匀化实施方法的FRP刚度预测

高涛1， 漆文凯1,2， 沈承1,2,*

1.南京航空航天大学 能源与动力学院， 南京 210016 2.江苏省航空动力系统重点实验室， 南京 210016

基于一种新的渐近均匀化(AH)实施方法，预测并讨论了单向纤维增强复合材料(FRP)的宏观等效弹性性能及纤维排列方式对等效力学性能的影响。该方法方便地将有限元分析(FEA)软件作为一个工具箱使用，只需在单胞上施加简单位移周期边界条件开展静力学分析，即可经过简单计算得到等效弹性常数，相比传统均匀化实施方法显著降低了实施难度并简化了计算过程。通过对比不同数值方法的结果验证了该方法的有效性和精确性。数值结果表明：六边形排列下单向纤维增强复合材料呈现横观各向同性，而正方形排列下则呈现宏观正交各向异性，经过刚度平均化过程可得到横观各向异性材料性质，纤维体积含量对两种排列方式下材料等效弹性模量影响显著但有所差别。

均匀化方法； 等效弹性性能； 周期边界条件； 有限元； 纤维排列； 复合材料

随着复合材料力学性能的优越性和可设计性得到了广泛的认可，越来越多的轻质高强复合材料被大量应用于航空、航天和船舶领域，如：飞机的机翼、机身和螺旋桨，火箭发动机壳体及船舶壳体等[1]。鉴于复合材料大多具有复杂的微细观结构，其宏观力学性质较难得到准确的预测。若能在设计阶段获知其宏观力学性能，将对复合材料的工程应用以及设计开发具有重要的价值，因此复合材料的等效宏观性能预测一直是材料及力学研究者关注的重要课题。

迄今为止，学者们提出了预测复合材料有效性能的许多模型和计算方法，详见综述文献[2-3]。其中，自洽(SCS)方法[4]、广义自洽(GSCS)方法[5]及Mori-Tanaka(M-T)方法[6]多被应用于推导具有简单微结构复合材料的数值解析公式[7-8]。而代表体元(Representative Volume Element，RVE)法[9]和渐近均匀化(Asymptotic Homogenization，AH)方法是近些年发展起来并得到广泛应用的数值计算方法，两者均可处理具有复杂周期性微结构的复合材料，且借助于有限元法便于实施和应用。具体来说，RVE法由于具有清晰的力学概念且应用过程较为简单，常被应用于复合材料以及点阵结构等效弹性性能的预测。例如，Sun和Vaidya[10]基于三维代表体单元和周期边界条件预测了复合材料的等效性能。Kanit等[11]提出了随机分布复合材料代表体积单元的定量选择模型。值得注意的是，RVE法并非基于严格的数学推导，因此一般仅适用于等效弹性性能的近似估计。

AH方法是一种基于摄动理论的多尺度数值等效方法，它通过近似求解定义在单胞上的偏微分方程进而得到材料的等效弹性性能[12]，该方法完整的推导过程可参考文献[13-14]。邢誉峰和陈磊[15]研究了摄动阶次和单元阶次对均匀化方法计算精度的影响，强调了二阶摄动对精度的作用。AH方法被广泛应用于求解各种材料和结构的等效弹性性能及宏细观应力分析[16-18]。例如，Hassan等[19]基于AH方法得到了三维编织复合材料、层合板、薄壁壳以及蜂窝夹芯三明治壳等结构的等效力学性能[20-23]。具体实施过程中，AH方法通常借助于有限元理论，需针对不同问题建立相应的有限元结构单元，进行大量编程和积分运算，操作起来比较复杂且求解效率比较低。为此，Cheng等[12]提出了一种基于渐近均匀化理论的新型有限元实施(Novel Implementation of Asymptotic Homogenization， NIAH)方法，已经被成功应用于蜂窝板的等效刚度预测[24]。该方法可以避免大量编程和积分运算，但实施过程中求解每个参数需对所有节点分3次加载等效初始位移场和周期性边界条件，加载分析过程较繁琐且运算量大。因此，本文改进了传统实施方法，可以更方便地借助于商业有限元软件作为工具箱来实施AH方法。通过引入一个新的特征函数(在Wang等的研究[25]中已有详细证明)，将原AH实施方法中的初始应变场和周期性边界条件简化成简单的位移型周期边界。新的实施方法借助于商业有限元软件作为工具箱，只需对单胞模型的边界施加简单位移型边界条件，进行一次静力分析，即可直接得到等效弹性常数。该方法具有广泛的适用性，可应用于具有周期性微结构的材料弹性性能预测，如纤维增强复合材料，格栅结构材料和点阵结构等。

众所周知，随机分布的长纤维增强复合材料(FRP)具有横观各向同性的材料性质。在以往的解析和数值研究中，通常利用正方形或六边形排列模型来预测其等效力学性能，其中纤维六边形排列模型可完全等效为横观各向同性，但正方形排列下的模型却具有正交各向异性的材料性质，这在以往的研究中通常被忽视。因此，深入分析排列方式对单向纤维增强复合材料等效力学性能的影响具有重要的理论价值。本文基于新的渐近均匀化实施方法，通过建立可考虑不同纤维排列方式的统一模型，系统研究了排列方式以及纤维体积含量对单向纤维增强复合材料等效弹性参数的影响。

1 新的渐近均匀化方法

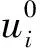
(1)

根据弹性力学基本理论，应变与位移、应力与应变的关系可以表示为

(2)

式中：εkl和σij为应变和应力张量；Eijkl为弹性常数张量。

根据虚位移原理，虚位移方程可以描述为

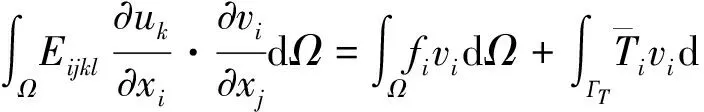
(3)

图1 周期结构及其单胞示意图 Fig.1 Periodic stucture and corresponding unit cell

将式(1)代入式(3)，线弹性单胞问题可以描述为[13]

(4)

对于如图2所示的长方体单胞，周期边界条件可以描述为

(5)

式中：U∓代表单胞沿y1正方向上的两个面；V∓代表单胞沿y2正方向上的两个面；W∓代表单胞沿y3正方向上的两个面。

等效弹性常数可由式(6)得到：

(6)

或写成矩阵形式为

(7)

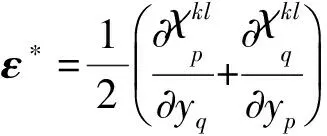
图2 长方体单胞 Fig.2 A rectangular parallelepiped unit cell

(8)

对于三维单胞问题，有

(9)

(10)

式中：δkn和δln为Kronecker函数，n取1，2，3。

通过引入这个特征函数，等效弹性常数式(6)可表示为

(11)

通过引入新的特征函数张量，原来的对单胞加载初始应变和周期边界条件的问题转化成简单的位移周期边界问题。周期性边界条件式(5)可以进一步简化为

(12)

结合式(5)和式(12)，简单位移型周期边界条件可以描述为6种初始位移边界加载，即

(13)

(14)

(15)

(16)

(17)

(18)

可以看出，这6种位移边界条件格式统一，只与单胞的尺寸有关，故加载更加简便。

根据文献[26]，式(11)可进一步表示为

(19)

矩阵形式为

(20)

(21)

2 新方法实施流程简述

图3 传统AH方法和新实施方法流程图 Fig.3 Flowcharts of traditional AH and new implementation methods

为了更清楚地展现新的方法，以及新实施方法和传统AH方法的不同和联系，绘制两者的流程图，如图3所示. 从对比流程图中可以看到，传统AH求解方法中，需要在每个单元上积分，这就要求必须清楚有限元单元的每一个细节，如形函数、本构关系和应变-位移矩阵。对于不同的单元类型，这些矩阵也都不同。因此必须针对不同单胞和单元自编不同的有限元模型、列式和程序并进行多次求解。在新的实施方法中，可以用商业有限元软件来完成建模和一次直接求解，比如ANSYS。新的方法实施起来更为简单方便，只需编写一个小的脚本，针对不同单胞不同单元，都可以直接计算，不用考虑具体的细节。商业软件作为一个工具箱，仅需要一次静力加载即可直接输出结果，大大简化渐进均匀化方法的实施流程，同时，无需自编程序和积分运算，提高了计算效率。在实施求解时也应注意：① 为了保证周期性边界条件的准确施加，有限元单胞模型在建模时需要在平行的两个边界面对应节点的保持对称性；② 若单胞模型采用二维单元或者一维单元(如壳或梁单元)，施加位移周期边界时需要将施加的节点平动自由度转换成转角自由度。

根据复合材料力学，横观各向同性材料的刚度系数与弹性模量的关系有

S=D-1=

(22)

式中:下标a和t分别代表纵向(即沿纤维方向)和横向(即垂直于纤维方向)；E、G和ν分别为弹性模量、剪切模量和泊松比。

本文基于商业有限元软件ANSYS建立单胞模型，为便于施加周期边界条件，单胞相对边界网格需保证完全一致，然后运用APDL语言可方便地施加初始位移场。等效刚度系数矩阵可由ANSYS结果直接输出，通过横观各向同性材料的刚度系数矩阵与弹性模量的关系式(22)最终得到材料等效弹性模量。

3 算例分析

3.1 有效性验证

图5为该单胞模型的有限元网格，基体和纤维结合部经适当加密。模型采用网格数为24 420的Solid185实体单元进行有限元离散。本例假设为硼/铝复合材料，纤维和基体材料参数为：Ef=379.3 GPa，νf=0.1；Em=68.3 GPa，νm=0.3,Vm=0.47。

图4 单向纤维增强复合材料及对应单胞示意图 Fig.4 Illustration of unidirectional fibre reinforced composite and corresponding unit cell

图5 单胞的有限元网格 Fig.5 Finite element mesh of unit cell

本文模型和其他模型对比结果见表1，其中，FEM[10]实际是一种基于有限元理论的数值逼近方法。GMC方法[27]、HFGMC方法[27]和ECM方法[28]是MOC方法[29]的变形，本质是利用Legendre多项式的不同阶形式对不同尺度下的位移进行展开。VAMUCH方法[30]是另外一种渐近展开法，它通过对单胞能量泛函渐进展开来预测有效弹性常数。从表1中可以看出，MOC和GMC预测的剪切模量G12偏小，而FEM方法预测的G12偏大，本文和另外一种渐进均匀化方法VAMUCH方法以及HFGMC方法计算的结果较为接近。诸多方法中，本文方法实施最为简单有效，且结果较精确，充分说明了该方法的有效性。

表1不同方法预测的硼/铝复合材料等效材料性能

Table1Equivalentmaterialpropertiesofbron/aluminumcompositesobtainedusingdifferentmethods

MethodE11/GPaE22/GPaG12/GPaG23/GPaν12ν23VAMUCH[30]215．3144．154．345．90．1950．255FEM[10]21514457．245．90．1950．29MOC[29]215142．651．343．70．200．25GMC[27]21514151．243．700．1950．261HFGMC[27]215．414454．345．830．1950．255ECM[28]215143．454．345．10．1950．26Present215．2143．954．345．810．1950．255

Notes：Ef=379.3 GPa,νf=0.1,Em=68.3 GPa,νm=0.3,Vm=0.47.

3.2 不同单胞模型对结果的影响

图6给出了同一纤维排列下选取不同单胞模型的示意图，表2列出了C1～C4相同纤维体积分数下不同单胞模型的弹性模量及泊松比结果，C4是经过坐标变换后的结果。结果显示：C1、C2和C3的结果完全一致，只有C4弹性模量有细小差别，这种细小的差异是由有限元网格本身的差异造成的。这说明同一纤维排列方式下，弹性模量的结果与单胞模型的选取无关。

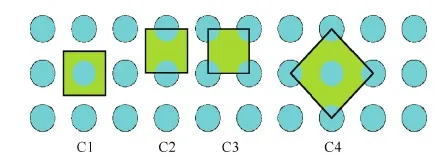
图6 不同的单胞模型 Fig.6 Different unit cell models

表2 不同单胞模型的结果Table 2 Results using different unit cell models

ModelofunitcellEa/GPaEt/GPaGt/GPaGa/GPaνaνtC137．9410．932．902．190．0870．410C237．9410．932．902．190．0870．410C337．9410．932．902．190．0870．410C437．9310．922．902．190．0870．410

Notes：Ef=73 GPa,νf=0.22,Em=2.9 GPa,νm=0.4,Vm=0.5.

3.3 正方形排列与六边形排列

图7 菱形纤维排列下复合材料的横截面和单胞 Fig.7 Cross-section and unit cell of composites with rhombic fiber arrangement

图8 单胞模型的有限元网格 Fig.8 Finite element meshes of unit cell model

图9 正方形纤维排列下的坐标变换 Fig.9 Coordinate transformation of square fiber arrangements

D′=T(θ)DTT(θ)

(23)

式中：T(θ)为坐标转换矩阵，且

(24)

其中：li,mi,ni(i=1,2,3)为方向余弦。

材料参数同表2。计算可得到等效刚度矩阵，再根据式(23)的坐标变换，得到两种纤维排列方式下等效刚度系数随θ的变化规律(如图10所示)。结果表明，两种纤维排列下任意θ(-45°≤θ≤45°)均满足如下关系：D11=D22,D13=D23,D44=D55,D16=-D26。纤维排列方式为六边形时，所有刚度系数都不随θ变化，说明该纤维排列下模型呈现为横观各向同性材料属性。纤维呈正方形排列时，模型呈现正交各向异性，只有D13(=D23),D33,D44(=D55)不随θ变化，并且其拉伸-弯曲耦合刚度系数D16(=-D26)在某些角度θ下并不为零。两种排列方式下刚度系数D13(=D23),D33,D44(=D55)非常接近。

为了消除转角对有效弹性常数的影响，令刚度系数在所有可能转角θ下取平均值，此时平均刚度系数可以表示为

(25)

式中：Dsquare(θ)为角度θ下的刚度矩阵。此时，正方形排列下平均化后的刚度矩阵为

(26)

平均化后的刚度矩阵不再随转角θ变化，进而可得到横观各向同性材料性质下的刚度矩阵，最终由式(22)获得等效弹性模量。

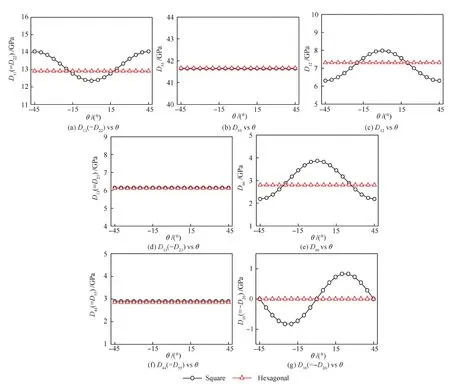
图10 两种纤维排列方式下的等效刚度系数随θ的变化 Fig.10 Variations of effective stiffness coefficients with θ for two fiber arrangements

3.4 纤维体积分数对弹性模量的影响

图11给出了正方形和六边形纤维排列下的拉伸和剪切模量随纤维体积分数变化曲线，其中，正方形排列的等效模量是经过刚度平均化后的结果。从图中可以看出：两种排列方式在相同体积含量下的纵向拉伸模量(Ea)相同，且都随纤维体积分数的增加呈线性增加。说明等效的纵向拉伸模量主要受纤维纵向拉伸模量的影响，与纤维体积分数有关，与纤维排列方式无关。在较低纤维体积含量(Vf≤0.35)下，正方形和六边形纤维排列方式下的横向拉伸模量(Et)、横向剪切模量(Gt)和纵向剪切模量(Ga)随纤维体积含量的增大缓慢增加，且两种排列下的值都非常接近，而在较高纤维体积含量(Vf>0.35)下，这些模量随纤维体积分数增大的速率不断增大，正方形排列下的模量都比六边形排列要大，且这种差距随纤维体积分数的增加而逐渐增大。总的来看，相同体积分数条件下，除了纵向拉伸模量外，正方形排列材料的拉伸和剪切弹性模量均大于六边形排列材料的。说明在较低纤维体积含量时，其横向拉伸模量、横向剪切模量和纵向剪切模量受基体材料的模量影响较大，在较高纤维体积含量时，这些模量受纤维材料的模量影响较大。物理机理[31]在于正方形排列纤维之间的最小间距比六边形排列时要小，即纤维排列更紧密，因此其等效横向拉伸模量和剪切模量更大。

图11 不同体积分数下的拉伸模量和剪切模量 Fig.11 Tensile modulus and shear modulus under different volume fraction

4 结 论

1) 基于一种新型渐近均匀化实施方法，建立了单向纤维增强复合材料的等效弹性性能预测模型。通过和其他理论对比，验证了该方法的准确性和简便性。

2) 数值结果表明：单胞的选取方式对求解结果没有影响；通过建立不同纤维排列方式下的统一单胞模型，可讨论排列方式对材料等效参数的影响，六边形排列下的单胞模型具有横观各向同性的材料性质，而正方形排列下的单胞模型则具有正交各向异性的性质，此时，可通过坐标变换和刚度平均化由正方形排列单胞模型得到横观各向同性的材料性质；此外，纤维体积含量对不同排列方式下材料的拉伸及剪切模量影响显著但有所差别。

[1] 杜善义, 章继峰, 张博明. 先进复合材料格栅结构(AGS)应用与研究进展[J]. 航空学报, 2007, 28(2): 419-424.

DU S Y, ZHANG J F, ZHANG B M. Overview of application and research on advanced composite grid structures[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 419-424 (in Chinese).

[2] DIXIT A, MALI H S. Modeling techniques for predicting the mechanical properties of woven-fabric textile composites: A review[J]. Mechanics of Composite Materials, 2013, 49(1): 1-20.

[3] YOUNES R, HALLAL A, FARDOUN F, et al. Comparative review study on elastic properties modeling for unidirectional composite materials[M]//Composites and Their Properties. Rijeka: InTech, 2012: 261-290.

[4] HILL R. A self-consistent mechanics of composite materials[J]. Journal of the Mechanics and Physics of Solids, 1965, 13(4): 213-222.

[5] CHRISTENSEN R M, LO K H. Solutions for effective shear properties in three phase sphere and cylinder models[J]. Journal of the Mechanics and Physics of Solids, 1979, 27(4): 315-330.

[6] MORI T, TANAKA K. Average stress in matrix and average elastic energy of materials with misfitting inclusions[J]. Acta Metallurgica, 1973, 21(5): 571-574.

[7] LIU X N, HU G K. A continuum micromechanical theory of overall plasticity for particulate composites including particle size effect[J]. International Journal of Plasticity, 2005, 21(4): 777-799.

[8] HU N, WANG B, TAN G W, et al. Effective elastic properties of 2-D solids with circular holes: Numerical simulations[J]. Composites Science and Technology, 2000, 60(9): 1811-1823.

[9] LIU T, DENG Z C, LU T J. Design optimization of truss-cored sandwiches with homogenization[J]. International Journal of Solids & Structures, 2006, 43(25-26): 7891-7918.

[10] SUN C T, VAIDYA R S. Prediction of composite properties from a representative volume element[J]. Composites Science and Technology, 1996, 56(2): 171-179.

[11] KANIT T, FOREST S, GALLIET I, et al. Determination of the size of the representative volume element for random composites: Statistical and numerical approach[J]. International Journal of Solids and Structures, 2003, 40(13-14): 3647-3679.

[12] CHENG G D, CAI Y W, XU L. Novel implementation of homogenization method to predict effective properties of periodic materials[J]. Acta Mechanica Sinica, 2013, 29(4): 550-556.

[13] BENSSOUSAN A, LIONS J L, PAPANICOLAOU G. Asymptotic analysis for periodic structures[M]. New York: North-Holland Publishing Co., 1978: 102-121.

[14] HASSANIA B, HINTON E. A review of homogenization and topology optimization I—Homogenization theory for media with periodic structure[J]. Computers and Structures, 1998, 69(6): 707-717.

[15] 邢誉峰, 陈磊. 若干周期性复合材料结构数学均匀化方法的计算精度[J]. 航空学报, 2015, 36(5): 1520-1529.

XING Y F, CHEN L. Accuracy analysis of mathematical homogenization method for several periodical composite structure[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1520-1529 (in Chinese).

[16] ANDRIANOV I V, DANISHEVS’KYY V V, WEICHERT D. Asymptotic determination of effective elastic properties of composite materials with fibrous square-shaped inclusions[J]. European Journal of Mechanics—A/Solids, 2002, 21(6): 1019-1036.

[17] ASKARI D, VEEDU V P, GHASEMI-NEJHAD M N. Chirality dependence of carbon single-walled nanotube material properties: Axial coefficient of thermal expansion[J]. Journal of Nanoscience & Nanotechnology, 2006, 6(7): 2167-2174.

[18] NASUTION M R E, WATANABE N, KONDO A, et al. Thermomechanical properties and stress analysis of 3-D textile composites by asymptotic expansion homogenization method[J]. Composites Part B: Engineering, 2014, 60: 378-391.

[19] HASSAN E M, GEORGIADES A V, SAVI M A, et al. Analytical and numerical analysis of 3D grid-reinforced orthotropic composite structures[J]. International Journal of Engineering Science, 2011, 49(7): 589-605.

[20] KALAMKAROV A L, GEORGIADES A V. Asymptotic homogenization models for smart composite plates with rapidly varying thickness: Part I—Theory[J]. International Journal for Multiscale Computational Engineering, 2004, 2(1): 133-148.

[21] CHALLAGULLA K S, GEORGIADES A V, KALAMKAROV A L. Asymptotic homogenization modeling of smart composite generally orthotropic grid-reinforced shells: Part I—Theory[J]. European Journal of Mechanics—A/Solids, 2010, 29(4): 530-540.

[22] GEORGIADES A V, CHALLAGULLA K S, KALAMKAROV A L. Asymptotic homogenization modeling of smart composite generally orthotropic grid-reinforced shells: Part II—Applications[J]. European Journal of Mechanics—A/Solids, 2010, 29(4): 541-556.

[23] KALAMKAROV A L, ANDRIANOV I V, DANISHEVS’KYY V V. Asymptotic homogenization of composite materials and structures[J]. Applied Mechanics Reviews, 2009, 62(3): 669-676.

[24] CAI Y W, XU L, CHENG G D. Novel numerical implementation of asymptotic homogenization method for periodic plate structures[J]. International Journal of Solids and Structures, 2014, 51(1): 284-292.

[25] WANG W X, LUO D M, TAKAO Y, et al. New solution method for homogenization analysis and its application to the prediction of macroscopic elastic constants of materials with periodic microstructures[J]. Computers and Structures, 2006, 84(15-16): 991-1001.

[26] SIGMUND O, TORQUATO S. Design of smart composite materials using topology optimization[J]. Smart Materials and Structures, 1999, 8(3): 365-379.

[27] ABOUDI J, PINDERA M J, ARNOLD S M. Linear thermoelastic higher-order theory for periodic multiphase materials[J]. Journal of Applied Mechanics, 2001, 68(5): 697-707.

[28] WILLIAMS T O. A two-dimensional, higher-order, elasticity-based micromechanics model[J]. International Journal of Solids and Structures, 2005, 42(3-4): 1009-1038.

[29] ABOUDI J. A continuum theory for fiber-reinforced elastic-viscoplastic composites[J]. International Journal of Engineering Science, 1982, 20(5): 605-621.

[30] YU W B, TANG T. Variational asymptotic method for unit cell homogenization of periodically heterogeneous materials[J]. International Journal of Solids and Structures, 2007, 44(11-12): 3738-3755.

[31] 许震宇， 张若京. 纤维排列方式对单向纤维加强复合材料弹性常数的影响[J]. 力学季刊, 2002, 23(1): 59-63.

XU Z Y, ZHANG R J. Influence of fibers’ packing modes on elastic constants of fiber reinforced polymer (FRP) material[J]. Chinese Quarterly of Mechanics, 2002, 23(1): 59-63 (in Chinese).

(责任编辑： 徐晓)

URL：www.cnki.net/kcms/detail/11.1929.V.20170217.1614.012.html

PredictionofFRPstiffnessbasedonanewimplementationofhomogenizationmethod

GAOTao1,QIWenkai1,2,SHENCheng1,2,*

1.CollegeofEnergyandPowerEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China2.JiangsuProvinceKeyLaboratoryofAerospacePowerSystem,Nanjing210016,China

Basedonanewimplementationofasymptotichomogenization(AH)method,themacroscopicequivalentelasticpropertiesofunidirectionalfiberreinforcedpolymer(FRP)andtheeffectoffiberarrangementontheequivalentmechanicalpropertieswerepredictedanddiscussed.Thismethodcanbeeasilyimplementedtoobtaintheeffectiveelasticconstantsusingcommercialfiniteelementanalysis(FEA)softwareasatoolbox,andnodaldisplacementfieldcorrespondingtotheunitstrainfieldwasappliedwithconsiderationofperiodicboundaryconditions.Comparedtotraditionalhomogenizationmethodsthismethodsignificantlyreducedthedifficultyofimplementationandsimplifiedthecalculationprocess.Acomparisonofseveralmethodsrevealsthatthisimplementationmethodissimpleandtheresultobtainedisaccurate.ThenumericalresultsshowfiberreinforcedpolymerwithhexagonalarrangementhastransverselyisotropicmaterialbehaviorbutFRPwithsquarearrangementhasorthotropicmaterialbehavior;astiffnessaveragenessprocedureisrequiredtoobtainthetransverselyisotropicstiffnessmatrixofFRP;thefibervolumefractionhasasignificantbutdifferenteffectontheequivalentelasticmodulusofthetwokindsofarrangement.

homogenizationmethod;equivalentelasticproperties;periodicboundarycondition;finiteelement;fiberarrangement;composites

2016-06-30；Revised2017-01-18；Accepted2017-01-23；Publishedonline2017-02-171614

s：AeronauticalScienceFoundationofChina(2013ZB52019);NationalNaturalScienceFoundationofChina(11502110);NaturalScienceFoundationofJiangsuProvinceofChina(BK20150737);theFundamentalResearchFundsforCentralUniversities(NJ20150005)

.E-mailcshen@nuaa.edu.cn

2016-06-30；退修日期2017-01-18；录用日期2017-01-23； < class="emphasis_bold">网络出版时间

时间：2017-02-171614

www.cnki.net/kcms/detail/11.1929.V.20170217.1614.012.html

航空科学基金 (2013ZB52019)； 国家自然科学基金 (11502110)； 江苏省自然科学基金 (BK20150737)； 中央高校基本科研业务费专项资金 (NJ20150005)

.E-mailcshen@nuaa.edu.cn

高涛， 漆文凯， 沈承. 基于一种新的均匀化实施方法的FRP刚度预测J． 航空学报,2017,38(5):220579.GAOT,QIWK,SHENC.PredictionofFRPstiffnessbasedonanewimplementationofhomogenizationmethodJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):220579.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.220579

V258+.3

A

1000-6893(2017)05-220579-11