翼伞系统在未知风场中的归航控制

陶金， 孙青林,*， 檀盼龙， 邬婉楠， 陈增强， 贺应平

1.南开大学 计算机与控制工程学院， 天津 300350 2.中德应用技术大学 电气与能源学院， 天津 300191 3.中国航空工业集团公司 宏伟航空器有限责任公司， 襄阳 441000

翼伞系统在未知风场中的归航控制

陶金1， 孙青林1,*， 檀盼龙2， 邬婉楠1， 陈增强1， 贺应平3

1.南开大学 计算机与控制工程学院， 天津 300350 2.中德应用技术大学 电气与能源学院， 天津 300191 3.中国航空工业集团公司 宏伟航空器有限责任公司， 襄阳 441000

翼伞系统在未知风场中执行归航任务时，需获得风场的大小和方向信息，以便在归航过程中利用或者消除风场的影响。为实现翼伞系统在未知风场中精确归航与逆风雀降着陆，首先提出一种利用全球定位系统(GPS)定位数据和最小二乘法在线辨识风向和风速的方法，然后将风场中平均风的影响在轨迹规划中予以考虑，设计分段归航路径；将突风作为外界干扰，在轨迹跟踪过程中由线性自抗扰控制(LADRC)器进行观测和补偿。最后通过仿真实验验证了本文所提出的归航控制方法对于提高翼伞系统在未知风场中的归航精度和抗风能力有重要意义。

翼伞系统； 未知风场； 风向辨识； 归航轨迹； 轨迹跟踪； 线性自抗扰控制(LADRC)

翼伞系统是一种拥有高升阻比气动性能、出色滑翔能力、良好操控性和稳定性的精确空投系统，一般由冲压型翼伞、负载和控制器组成。鉴于其诸多的优点，翼伞系统在众多的领域得到应用。如在现代化战争中，地面作战部队可以通过翼伞空投实现武器、弹药、给养的及时补充；在发生重大自然灾害时，可以通过翼伞精确空投的方式第一时间将救灾物资和设备运输到灾害中心，完成紧急救援任务；在航空航天领域，大型翼伞系统可用于航天飞船、卫星等设备的安全回收；在民用领域，翼伞系统可用于运动、观光、农业植保等。近些年来，随着全球定位系统 (Global Position System，GPS)导航技术的成熟、测量技术和控制科学的发展，使得翼伞系统的自主归航控制研究方兴未艾[1]。

翼伞是由柔性纺织材料制成，在充气张满后飞行速度较低，因此易受到风场影响[2-3]。翼伞系统在执行归航任务时，有针对性的设计对风场处理的控制策略有助于提高翼伞系统的归航精度，保障其稳定飞行。实施雀降操纵要将翼伞系统逆风对准目标点[4-5]。以上工作的基本前提是风场已知，因此研究风场辨识方法对于实现精确归航具有重要意义。

翼伞系统的归航控制方法一般包括简单归航法、最优控制归航法和分段归航法。最早开展研究的是以径向归航、锥型归航为代表的简单归航方法，其控制简单，但是着陆的精度很大程度上取决于初始投放位置，且无法保证逆风[6]。目前研究较多的是最优控制归航法和分段归航法。最优控制归航法是在最优控制理论基础上发展起来的一种归航方法，通过优化翼伞系统的控制序列达到逆风雀降、能量最优的精确着陆。然而大多数的最优或者次优控制归航方法都停留在理论研究阶段[7-8]。分段归航法在20世纪90年代后在工程中被大量研究和应用，其主要思路是将翼伞系统整个归航轨迹按照不同的阶段和特点进行分段，然后根据最终着陆的要求对各段的参数进行优化。虽然分段归航法不能实现能耗最优，但分段轨迹可以进行准确的参数化描述，便于实现轨迹跟踪控制。文献[9-11]对分段归航法有所介绍，但是基本上只有分段的描述，没有提及如何实现的问题。文献[12]给出了具体的分段轨迹规划方法，但在研究过程中没有考虑风场大小和方向的影响。

控制策略的选择很大程度上取决于翼伞系统所采用的归航方法。针对简单归航，通常采用递推控制法来控制翼伞系统。最优归航法同时确定轨迹和控制量，一般采用开环控制方法。针对分段归航方案，需设计轨迹跟踪策略，典型的翼伞系统轨迹跟踪控制成果主要有文献[12]通过将翼伞系统的航迹跟踪问题简化为线性系统的输出跟踪问题，采用增益调节型模糊比例-微分(Proportion Differentiation，PD) 控制算法设计了航迹跟踪控制器。文献[13]利用拉格朗日插值法得到期望输出航向，并将模型预测控制的方法应用于翼伞系统轨迹跟踪控制。文献[14]将L1自适应控制方法应用在大型翼伞的航迹跟踪控制中。在实际翼伞空投应用中，ALEX型翼伞空投系统使用了简单的比例控制器进行归航控制[10]；Pegasus翼伞空投系统也使用了比例-积分-微分(Proportion Integration Differentiation，PID) 算法进行轨迹跟踪控制[15]。在轨迹跟踪研究中，通常的做法是将风的影响整个的看做外界的干扰来处理，由控制器加以修正。需要指出的是，控制器的抗风性能总是有一定限度的，风速过大会导致翼伞攻角过大或过小，造成系统失稳。因此，在归航控制策略设计中，针对性的对风场进行处理是必要的。

为克服未知风场对翼伞系统归航精度产生的影响，本文首先针对风场辨识问题，提出了一种基于仅利用GPS定位信息进行在线风场辨识的方法，然后在归航轨迹规划中考虑辨识的风向和风速信息，在轨迹跟踪控制中，将离散突风作为外界干扰，设计一种基于线性自抗扰控制(Linear Active Disturbance Rejection Control，LADRC)的轨迹跟踪控制器进行修正。仿真结果验证了本文所提出的未知风场中翼伞系统归航控制方法的可行性和有效性。

1 翼伞系统动力学模型

由于伞绳、吊带和连接带所选用的材料通常强度大、形变小，因此可忽略各绳索发生的弹性形变，从而限制了伞体和负载之间的相对滚转运动，只考虑两体之间的相对俯仰和相对偏航运动，建立翼伞系统八自由度动力学模型[16]，包括伞体的六个自由度和负载的两个相对伞体的转动自由度。

令Vp=[upvpwp]和Wp=[ppqprp]分别表示伞体的速度和角速度，Vw=[uwvwww]和Ww=[pwqwrw]分别表示负载的速度和角速度。利用动量和动量矩定理分别对伞体和负载进行分析，得

(1)

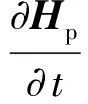
(2)

(3)

(4)

式中：下标p和w分别表示伞体和负载；上标aero、f、g和t分别表示气动力、摩擦力、重力和吊绳拉力；F和M分别为力和力矩。

伞体和负载的动量P和动量矩H表示为

(5)

(6)

式中：Aa和Ar分别为伞体的附加质量和真实质量矩阵；mw和Jw分别为负载的质量和转动惯量。

伞体和负载通过绳索连接，两者之间存在的约束关系为

Vw+Ww×Lw-c=Vp+Wp×Lp-c

(7)

Ww=Wp+τp+κw

(8)

式中：τp=[0 0ψr]，κw=[0θr0]，ψr和θr分别为伞体和负载的相对偏航角和相对俯仰角；Lw-c和Lp-c分别为负载质心和伞体质心到负载上两个悬挂绳的中心点C的距离。

联合式(1)～式(8)可以得到翼伞系统的八自由度的动力学模型，详细的建模推导过程参见文献[16]。

2 风场辨识方法

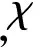
V、V0和Vf共同组成了翼伞系统在风场中的运动矢量三角形，根据图中所示的矢量关系可以得到

(9)

式中：Vx和Vy分别为V在x轴和y轴方向的速度分量；Vf,x和Vf,y分别为Vf在x轴和y轴方向的速度分量。

对式(9)中的两部分进行平方求和，并在翼伞系统的运动轨迹上取3个点，假设风速Vf不变，又因翼伞系统的空速V0是不变的，地速V可以通过GPS模块定位获得，进一步推导可得

(10)

图1 翼伞系统速度矢量关系图 Fig.1 Velocity vectors diagram of parafoil system

式中：Vi(i=1,2,3) 为位置点i相应的地速，Vxi和Vyi分别表示Vi在x轴和y轴方向上的速度分量。

至此，风场辨识即转化为求解二元一次方程组的问题，方程组的解即为风速在坐标轴的分量，表示为

(11)

引入带遗忘因子λ的最小二乘法实现对风场辨识结果的迭代更新，可得到风场辨识的更新公式。具体的推导过程见文献[5]。

3 分段归航轨迹规划

3.1 分段归航策略

利用辨识的风速和风向信息，在大地坐标系下对翼伞系统归航轨迹进行分段设计。考虑风场的最终作用效果，将整个飞行过程中风的影响转化为最终着陆目标点的偏移和着陆方向的偏转。因此，在初始投放高度确定的情况下，水平面的轨迹规划就是以虚拟目标点Gf为规划目标点，选择合适的圆弧和线段的组合。本文选择一种经典的分段归航策略[12]进行改进，如图2所示。图中，A点为翼伞空投系统的初始投放位置，Gr为实际着陆目标点，Gf为虚拟规划目标点，β1、β2、β3和β4分别表示分段轨迹AB、CD、DE和EF所对应的圆心角，γ为风场方向，两目标点连线GfGr与x轴的夹角也为γ，两目标点之间的距离可表示为

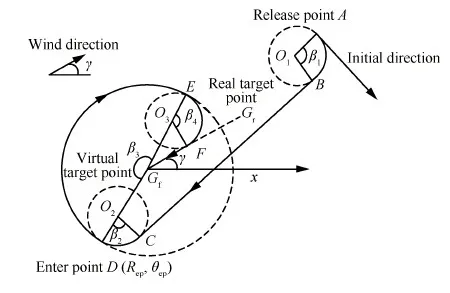
图2 分段归航轨迹规划 Fig.2 Multiphase homing trajectory planning

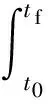
(12)

式中：t0为投放初始时刻；tf为着陆时刻，对于投放高度h已知的情况下，tf=h/vz，其中vz为翼伞系统平均下降速度。

分段轨迹优化的关键在于确定翼伞系统进入能量控制阶段DE的切入点D的位置，可用能量控制阶段圆形轨迹的半径Rep和虚拟目标点Gf和D点的连线与x轴的夹角θep来表示。翼伞系统归航轨迹规划的目的是实现着陆点与目标点距离最小，并在着陆时刻逆风，据此分段轨迹目标函数J定义为

J=|Rmin(β1+β2+β4)+Repβ3+

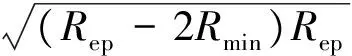
(13)

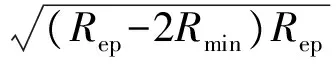
综上，利用大地坐标系下各分段的几何关系，将翼伞系统分段归航轨迹规划问题转化为参数优化问题。

3.2 优化算法

由于目标函数J定义为隐函数，无法显式表达，且被优化参量为实数，数目较少，因此所选用的优化算法应具有较好的搜索能力和精度以及较高的鲁棒性。本文选用一种改进的粒子群优化(Modified Particle Swarm Optimization,MPSO)算法作为J的优化算法。

在基本PSO中，初始种群通常为随机选取，当可行解空间较大时，不能保证初始粒子均匀分布，因此会减弱算法的全局搜索能力。算法在寻优过程中遇到局部极值，非常容易致使所有粒子都飞入该极值点停滞不前导致算法早熟[17-18]。这时就需要在算法中加入扰动，使部分粒子跳出局部极值点。

混沌优化算法具有对初值不敏感、易跳出局部极值、全局渐近收敛的特点[19]。混沌优化算法是把混沌变量从混沌空间映射到可行性解空间，然后利用混沌变量的遍历性进行搜索。本文提出的MPSO主要利用混沌算法在以下两方面改进基本PSO：① 混沌初始化种群代替随机初始化种群，使得初始粒子分布更加均匀；② 在最优解周围的区域内进行混沌迭代，以增强种群粒子的多样性，防止算法进入早熟。

本文采用Logistic混沌映射

Pi,N=4Pi-1,N(1-Pi-1,N)

(14)

式中：i=2,3,…,L，L为混沌初始化的种群数量；Pi,N为i×N维的随机数。

4 基于LADRC的轨迹跟踪控制

4.1 基于制导的2D轨迹跟踪策略

计算跟踪轨迹误差时，借鉴Breivik和Fossen提出的基于制导的路径跟踪的概念[20]，采用基于制导的2D轨迹跟踪策略设计翼伞系统轨迹跟踪的制导律，如图3所示。

假设跟踪目标是参考轨迹上的运动目标点pp，而pp的位置是按照尺度变量ϖ更新的，表示为pp(ϖ)=[xp(ϖ)yp(ϖ)]T，其变化率表示为

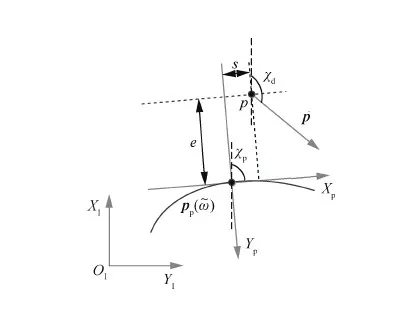
图3 基于制导的2D轨迹跟踪策略示意图 Fig.3 Geometric sketch of 2D guidance based trajectory tracking scheme

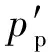
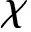
(15)

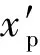
以pp的运动方向为x轴建立参考轨迹坐标系，为了将惯性坐标系下的描述转到参考轨迹坐标系下进行描述，建立旋转矩阵

(16)

因此，任意点p到参考轨迹点pp的距离误差表示为

(17)

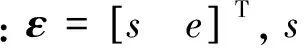
利用关于误差的李雅普诺夫函数可以证明在轨迹跟踪过程中，其前向误差s和横向误差e满足一定的约束条件是收敛的，具体证明过程见文献[20]。

对于翼伞系统来讲，在轨迹跟踪过程中的参考目标点pp对参考速度和尺度变量进行更新可以实现前向误差s的消除，因此只需设置横向控制器控制翼伞系统的偏航角ψ跟踪给出的参考方向角就能消除横向误差e。

4.2 LADRC控制器设计

ADRC是由中科院的韩京清研究员提出的一种新型控制方法。ADRC继承了PID不依赖于被控对象数学模型的优点，通过采用扩张状态观测器估计系统扰动，将系统扰动补偿为串联积分型，从而实现扰动抑制[21]。 ADRC最初是以一种非线性形式提出的，具有较多的整定参数，不易调试。随后，美国克里夫兰州立大学的高志强教授通过带宽参数化的方法，将ADRC简化为LADRC，易于调试和工程实现[22]。近些年来，ADRC以其良好的控制效果，在多个领域得到了推广应用[23-25]。

翼伞系统与跟踪轨迹之间的横向误差可以通过控制翼伞系统偏航角ψ进行消除，结合翼伞系统动力学方程，可得如下形式的翼伞系统偏航角的二阶形式：

(18)

式中：f1(·)为关于翼伞系统状态变量的表达式；f2(u)为含有控制量u的表达式。

为了便于LADRC控制器的设计，将式(18)改写为

(19)

令f=f1(·)+f2(u)-b0u，将f视为翼伞系统总扰动，构造翼伞系统航迹方位角的线性扩张状态观测器(Linear Extended State Observer, LESO)，利用LESO估计出翼伞系统当前航迹方位角、方位角的变化率及整个系统的总扰动，再通过误差状态反馈控制率的动态补偿，从而实现对翼伞系统航迹方位角的跟踪控制。

由于实际系统状态观测器存在瞬态响应极值，为避免系统输出饱和，引入饱和限幅函数sat(·)，限幅方式选取

(20)

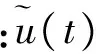
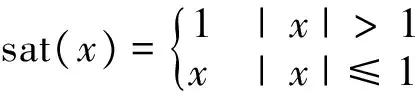
(21)

5 仿真实验

5.1 仿真环境设置

作为仿真实例，本文选用某一实际空投翼伞进行仿真实验，具体参数如表1所示。

根据所选的伞型，其初始运动参数为：初始速度(u,v,w)=(15.9,0,2.1) m/s,初始欧拉角(ξ,θ,ψ)=(0,0,0),初始角速度(p,q,r)=(0,0,0)。

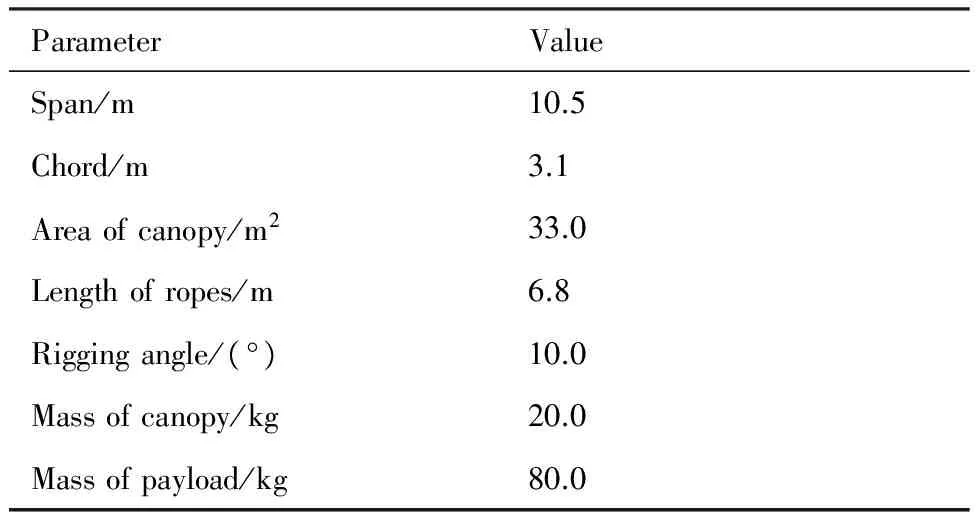
表1 翼伞系统参数Table 1 Parameters of parafoil system

为验证翼伞系统在未知风场中的归航控制方法，设置以下4种初始工况进行翼伞系统归航仿真实验，如表2所示。表中：(x0,y0,z0)为翼伞系统初始空投位置，α0为翼伞系统初始速度方向，(xf,yf,zf)为在仿真环境中加入的风场，这里，风场的大小和方向对于执行归航任务的翼伞系统是未知的，需要通过风场辨识的方法获得。设置着陆目标点为(0,0,0)。为了验证控制器的抗扰性，在115 s时刻向仿真环境中加入最大风速为3 m/s，方向沿y轴正向的NASA离散突风[26]。

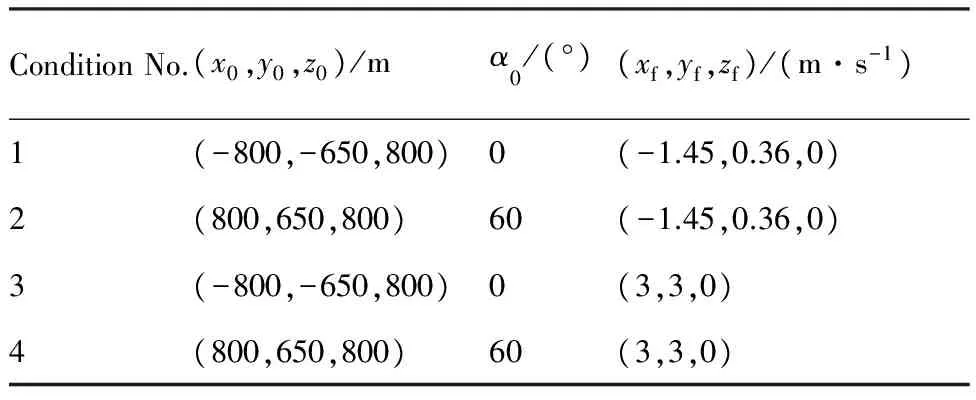
表2 初始工况Table 2 Initial conditions

MPSO参数设置如下：混沌初始化种群规模为100，种群规模为50，最大迭代次数为100；Rep的搜索空间为[245,500] m，θep的搜索空间为[-π,π]，扰动量设置为0.1。

采用本文构建的LADRC控制器与相同结构的PID控制器分别控制翼伞系统进行轨迹跟踪，最大控制量M=5。LADRC控制器的参数设置为：LESO带宽ωo=30，kP=0.18，kD=1，b0=0.04。PID控制器的参数设置为：kP=20，kD=100，kI=0.2。

5.2 工况1仿真结果

5.2.1 风场辨识

根据风场辨识原理，可在线辨识出翼伞系统在稳定转弯时的风速和风向，如图4所示。

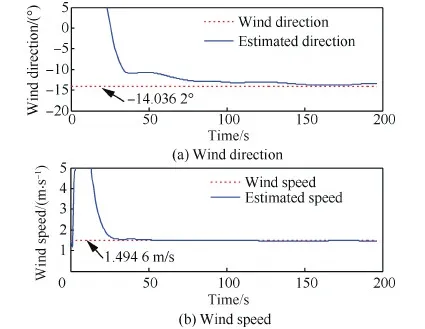
图4 风场辨识结果 Fig.4 Wind identification results

在使用最小二乘法进行递推更新时，所有的参数在初始化过程中设为0，因此在初始前25 s辨识值都是无效数据。从30 s开始风速和风向就能达到稳定的辨识效果。风向辨识结果的最终误差小于0.5°，风速辨识结果的最终误差小于0.1 m/s。可知，该风场辨识方法在风速和风向上均有较高的辨识精度。

5.2.2 分段轨迹规划

根据风场辨识结果，风向角γ=-14°，规划目标点Gf=(-400,100) m，基于MPSO优化所得的分段归航轨迹最优参数为Rep=330.3 m，θep=1.2 rad。规划出的分段归航轨迹如图5所示。从图中可看出，该分段归航轨迹能够实现翼伞系统在设定初始状态下的定点精确归航并在着陆时刻实现逆风对准。由于不考虑风场的中间作用效果，所规划归航轨迹为标准的圆弧和直线的组合，便于参数化，易实现跟踪控制。

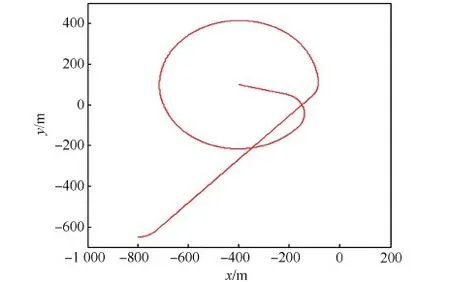
图5 分段归航轨迹 Fig.5 Multiphase homing trajectory

5.2.3 轨迹跟踪控制

分别利用LADRC和PID控制器在仿真风场环境中进行轨迹跟踪控制，图6～图8所示为仿真结果。

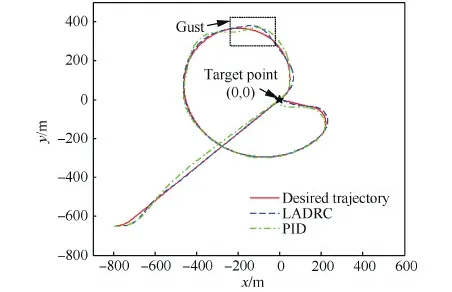
图6 平面轨迹跟踪效果 Fig.6 Trajectory tracking results on horizontal plane

图7 下偏操纵量 Fig.7 Deflection output

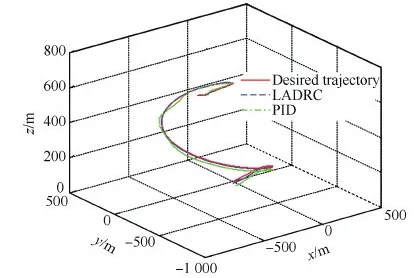
图8 三维空间轨迹跟踪效果 Fig.8 Trajectory tracking result in 3D space

图6为风场作用下理想分段归航轨迹以及LADRC和PID控制器控制翼伞系统跟踪规划轨迹在大地坐标系的效果图。由图中可知，两种控制器均能在风场影响下取得较好的轨迹跟踪效果。由于实际风场的影响贯穿了整个归航过程，翼伞系统跟踪轨迹随风场发生了一定的偏移，导致实际跟踪轨迹并不是由标准的圆弧和直线组成。由于平均风的影响在轨迹规划中予以考虑，在轨迹跟踪时可完全忽略，将突风视为外界干扰，在轨迹跟踪阶段由控制器修正。LADRC控制器将这种干扰作为系统的总扰动通过LESO进行观测并动态补偿，实现跟踪误差修正。从轨迹跟踪效果来看，LADRC控制器比PID控制器具有更高的轨迹跟踪精度。尤其在加入横向突风干扰后，两种控制器水平面轨迹都会有所偏移，跟踪误差增大，但LADRC控制器具有更快的跟踪误差收敛速度。LADRC控制器最终着陆偏差为2.3 m，而PID控制器着陆偏差为27.3 m。

图7为两种控制器输出的下偏操纵量曲线。其中，LADRC控制器输出在突风作用下产生震荡，在突风消失后迅速稳定，而PID控制器输出则处于较长时间的波动状态。

图8为翼伞系统三维空间下轨迹归航效果。从图中可以看出，翼伞系统在三维空间内能够较好的跟踪规划归航轨迹。一般来讲，传统的飞行器可对航迹倾斜角进行控制，但对于翼伞系统而言，由于双侧下偏操纵对翼伞系统纵向下降速度影响不大，翼伞系统以固定的航迹倾斜角向前做滑翔运动，由于在归航轨迹规划中充分考虑了翼伞系统的运动特性，因此翼伞系统归航轨迹与规划轨迹在纵向面也能够较好的吻合。

图9～图12为LADRC控制器控制翼伞系统跟踪归航轨迹过程中的状态变化情况。

图9为翼伞系统速度变化曲线。从图中可以看出，在整个归航过程中，翼伞系统的速度基本保持不变，其水平速度基本维持在11.1 m/s,垂直速度保持在2.8 m/s，在水平突风扰动下，其水平速度和垂直速度均发生了一定程度的震荡，这是由于翼伞系统水平面运动和纵向面运动存在着强耦合导致。由于惯性的存在，负载的水平速度和垂直速度在过渡阶段和风扰阶段总是略大于伞体的水平速度值。

图10为翼伞系统归航过程中滚转角变化曲线。由图可知，翼伞系统的滚转角仅在叠加突风作用时，波动较大，在稳定转弯或滑翔时，基本保持稳定。图11为翼伞系统俯仰角和相对俯仰角变化曲线。从图中可知，在翼伞系统归航过程中，伞体俯仰角基本稳定在-6.2°，负载与伞体之间的相对俯仰角维持在7.1°。在突风作用下，系统俯仰角震荡剧烈，相对俯仰角小幅波动。图12为翼伞系统在归航过程中的偏航角和相对偏航角变化曲线。从图中可知，其偏航角随着分段轨迹规律的变化，受突风影响较小；负载和伞体之间的相对偏航角则保持稳定，但在突风作用时产生高频振荡。

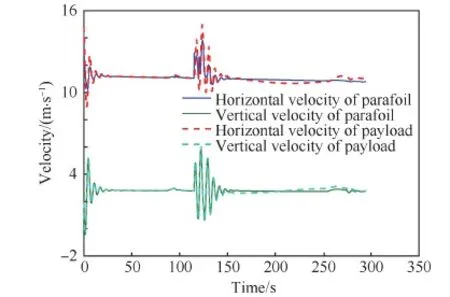
图9 速度变化曲线 Fig.9 Changing curves of velocities

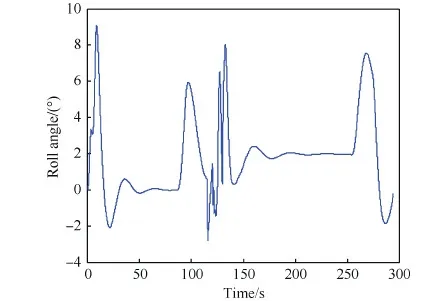
图10 滚转角变化曲线 Fig.10 Changing curves of roll angle

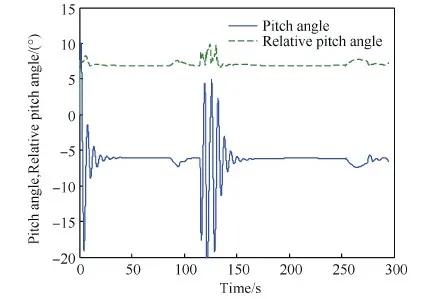
图11 俯仰角与相对俯仰角变化曲线 Fig.11 Changing curves of pitch angle and relative pitch angle

图12 偏航角与相对偏航角变化曲线 Fig.12 Changing curves of yaw angle and relative yaw angle

综上可知，翼伞系统在归航过程中可以保持自身姿态稳定，没有出现失速或失稳状况。

5.3 其他工况仿真结果

为简单起见，这里仅给出工况2～4下仿真得到的辨识风场的大小Vf和方向角γ，分段归航轨迹最优参数Rep和θep，以及分别利用LADRC和PID控制器进行轨迹跟踪控制最终着陆误差，如表3所示。

从表3中数据可以看出，风场对于翼伞系统归航精度的影响很大，随着风场强度的增大，着陆误差有增大的趋势。而采用本文提出的归航控制策略，在任一工况下，翼伞系统均能够较好跟踪规划好的归航轨迹准确的飞向目标点，且在目标点位置实现逆风对准。

表3 归航结果Table 3 Homing results

5.4 对比实验

作为比较，采用文献[12]提及的常用控制策略，即轨迹的规划在大地坐标系下进行，将风的影响整个的看做外界的干扰，与本文提出的归航控制策略相比，两者的区别在于对稳定平均风的处理。采用与3.1节类似的忽略所有风场影响的分段轨迹规划方案以及5.1节相同的LADRC和PID控制策略分别在表2所示的4种工况下进行归航实验，归航最终结果如表4所示。

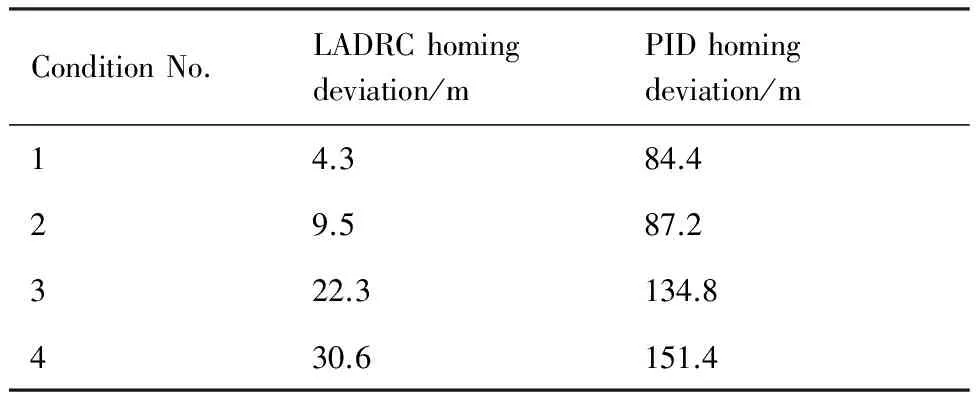
表4 常用控制策略归航结果Table 4 Results of homing with common control strategy

从表4中可以看出，采用普通归航控制方法，LADRC和PID控制器也都能实现一定精度的归航。与本文提出的归航控制策略相比，采用普通归航方法，两种控制器的归航偏差均增大。其中LADRC控制器的着陆偏差增幅较小，这得益于LADRC控制器良好的抗干扰能力。而PID控制器着陆偏差增幅较大，这是由于平均风的强干扰导致的。平均风与突风不同，其作用时间长，对翼伞系统而言，其对轨迹的影响仅依靠控制系统一般是难以消除的。因此，本文提出的归航控制方法可以减小风场尤其是较大风场扰动下对轨迹跟踪控制的影响和由此带来的系统失稳，对于提高翼伞系统的抗风性能和着陆精度有重要意义。

6 结 论

1) 通过GPS定位数据计算得到翼伞系统的飞行速度和方向，通过速度矢量三角形，采用最小二乘法实现了对风速和风向的在线辨识，仿真结果表明，该风场辨识方法可以有效准确的辨识出未知风场的风速和方向信息。

2) 考虑环境中风速和风向信息，对翼伞系统归航轨迹采用分段设计方法，引入虚拟着陆点的概念，将整个飞行过程中风的影响转化为着陆目标点的偏移和着陆方向的偏转，仿真结果表明，基于风场的归航轨迹规划方法能够规划出满足归航精度和逆风着陆的要求归航轨迹。

3) 借鉴基于制导的翼伞系统2D轨迹跟踪策略，通过李雅普诺夫方法得出了翼伞系统飞行的制导律，将对平面轨迹的跟踪问题转化为对翼伞系统航迹方位角的控制问题，并设计了基于LADRC的翼伞系统轨迹跟踪控制器。仿真结果表明，基于LADRC的轨迹跟踪控制器能够克服环境干扰，实现归航轨迹快速平稳跟踪，比PID控制器具有更好的控制精度和鲁棒性。

4) 本文提出的一整套归航控制方法较好的利用或消除了未知风场的影响，提高了翼伞系统归航过程中的抗风能力和着陆精度。

[1] YAKIMENKO O A. Precision aerial delivery systems: Modeling, dynamics, and control[M]. Reston: AIAA, 2015: 2-16.

[2] 朱旭, 曹义华. 翼伞平面形状对翼伞气动性能的影响[J]. 航空学报, 2011, 32(11): 1998-2007.

ZHU X, CAO Y H. Numerical simulation of planform geometry effect on parafoil aerodynamic performance[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 1998-2007 (in Chinese).

[3] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33(7): 1189-1200.

ZHU X, CAO Y H. Effects of arc-anhedal angle, airfoil and leading edge cut on parafoil aerodynamic performance[J]. Acta Aeronautica et Astronautica Sinica， 2012, 33(7): 1189-1200 (in Chinese).

[4] 张兴会, 朱二琳. 翼伞系统雀降性能及控制研究[J]. 航天控制, 2012, 30(1): 29-33.

ZHANG X H, ZHU E L. The study of the flare-landing performance and control of parafoil system[J]. Aerospace Control, 2012, 30(1): 29-33 (in Chinese).

[5] 檀盼龙， 孙青林， 高海涛， 等． 动力翼伞系统空投风场的辨识与应用[J]． 航空学报, 2016, 37(7): 2286-2294.

TAN P L, SUN Q L, GAO H T, et al. Wind identification and application of the powered parafoil system[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2286-2294 (in Chinese).

[6] LI Y, LIN H. Theoretical investigation of gliding parachute trajectory with deadband and non-proportional automatic homing control[C]//11th AIAA Aerodynamic Decelerator Systems Technology Conference. Reston: AIAA, 1991: 42-47.

[7] ZHANG L M, GAO H T, CHEN Z Q, et al. Multi-objective global optimal parafoil homing trajectory optimization via gauss pseudospectral method[J]. Nonlinear Dynamics, 2013, 72(1-2): 1-8.

[8] TAO J, SUN Q L, ZHU E L, et al. Quantum genetic algorithm based homing trajectory planning of parafoil system[C]//34th Chinese Control Conference (CCC). Piscataway, NJ: IEEE Press, 2015: 2523-2528.

[9] SIM A G, MURRAY J E, NEUFELD D C, et al. Development and flight testing of a deployable precision landing system[J]. Journal of Aircraft, 1994， 31(5): 1101-1108.

[10] JANN T. Advanced features for autonomous parafoil guidance, navigation and control: AIAA-2005-16428[R]. Reston: AIAA, 2005.

[11] SOPPA U, STRAUCH R. GNC concept for automated landing of a large parafoil: AIAA-1997-1464[R]. Reston: AIAA, 1997.

[12] 熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科学技术大学, 2005: 95-104.

XIONG J. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005: 95-104 (in Chinese).

[13] SLEGERS N J，YAKIMENKO O A．Optimal control for terminal guidance of autonomous parafoils: AIAA-2009-2958[R]. Reston: AIAA, 2009．

[14] BENJAMIN S C. Adaptive control of a 10K parafoil system: AIAA-2015-2107[R]. Reston: AIAA, 2015.

[15] KAMINER I I, YAKIMENKO O A. On the development of GNC algorithm for a high-glide payload delivery system[C]//42th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2003: 5438-5443.

[16] ZHU E L, SUN Q L, TAN P L, et al. Modeling of powered parafoil based on Kirchhoff motion equation[J]. Nonlinear Dynamics, 2015, 79(1): 617-629.

[17] 司维超, 韩维, 史玮韦. 基于PSO算法的舰载机舰面布放调度方法研究[J]. 航空学报, 2012, 33(11): 2048-2056.

SI W C, HAN W, SHI W W. Research on dech-disposed scheduling method of carrier planes based on PSO algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2048-2056 (in Chinese).

[18] 李丁, 夏露. 改进的粒子群优化算法在气动设计中的应用[J]. 航空学报, 2012, 33(10): 1809-1816.

LI D, XIA L. Application of improved particle swarm optimization algorithm to aerodynamic design[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1809-1816 (in Chinese).

[19] 刘玲, 钟伟民, 钱锋. 改进的混沌粒子群优化算法[J]. 华东理工大学学报(自然科学版), 2010, 36(2): 267-272.

LIU L, ZHONG W M, QIAN F. An improve chaos-particle swarm optimization algorithm[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2010, 36(2): 267-272 (in Chinese).

[20] BREIVIK M, FOSSEN T I. Principles of guidance-based path following in 2D and 3D[C]//44th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 2005： 627-634.

[21] HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.

[22] GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//American Control Conference. Piscataway, NJ: IEEE Press, 2003： 4989-4996.

[23] ZHANG H B, WANG J K, CHEN G Q, et al. A new hybrid control scheme for an integrated helicopter and engine system[J]. Chinese Journal of Aeronautics, 2012, 25(4): 533-545.

[24] 李自行, 李高风. 移动质心再入飞行器建模及自抗扰滚动控制[J]. 航空学报, 2012, 33(11): 2121-2129.

LI Z X, LI G F. Moving centroid reentry vehicle modeling and active disturbance rejection roll control[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2121-2129 (in Chinese).

[25] 王彦雄, 祝小平, 周洲, 等. 穿越微下冲气流的飞翼布局无人机控制方法[J]. 航空学报, 2015, 36(5): 1673-1683.

WANG Y X, ZHU X P, ZHOU Z, et al. A control method of flying wing UAV for penetration of microburst[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1673-1683 (in Chinese).

[26] 熊菁, 秦子增, 程文科. 回收过程中高空风场的特点及描述[J]. 航天返回与遥感, 2003, 24(3): 9-14.

XIONG J, QIN Z Z, CHENG W K. The characteristics and description of mid-high altitude wind in recovery[J]. Spacecraft Recovery and Remote Sensing, 2003, 24(3): 9-14 (in Chinese).

(责任编辑： 张玉， 李世秋)

URL：www.cnki.net/kcms/detail/11.1929.V.20170220.0926.002.html

Homingcontrolofparafoilsystemsinunknownwindenvironments

TAOJin1,SUNQinglin1,*,TANPanlong2,WUWannan1,CHENZengqiang1,HEYingping3

1.CollegeofComputerandControlEngineering,NankaiUniversity,Tianjin300350,China2.ElectricalEngineeringandEnergyCollege,Sino-GermanUniversityofAppliedSciences,Tianjin300191,China3.HongweiAircraftCo.,Ltd.,AviationIndustryCorporationofChina,Xiangyang441000,China

Itisimportantforparafoilsystemsinperforminghomingtasksinunknownwindenvironmentstoidentifythespeedanddirectionofthewind,soastotakeadvantageoreliminateimpactsofthewindinthehomingprocess.Torealizeaccuratehomingandflarelanding,awindidentificationmethodusingglobalpositionsystem(GPS)informationandleastsquaremethodisproposedtotheestimateunknownwinddisturbances.Amultiphasehomingtrajectoryisplannedwithconsiderationoftheinfluencesofthemeanwinds.Ahomingtrajectorytrackingcontrollerisdesignedbasedonlinearactivedisturbancerejectioncontrol(LADRC)strategytoobserveandcompensatethedisturbancesofgusts.Simulationexperimentsofhominginunknownwindyconditionsareconducted.Theresultsdemonstratethattheproposedhomingcontrolmethodisofgreatimportanceforimprovinghomingaccuracyandwindresistanceabilityofhomingofparafoilsystemsinunknownwindenvironments.

parafoilsystem;unknownwindenvironment;windidentification;homingtrajectory;trajectorytracking;linearactivedisturbancerejectioncontrol(LADRC)

2016-06-11；Revised2016-07-19；Accepted2016-09-20；Publishedonline2017-02-200926

s：NationalNaturalScienceFoundationofChina(61273138,61573197);KeyFundofTianjin(14JCZDJC39300);NationalKeyTechnologyResearchandDevelopmentProgramofChina(2015BAK06B04);KeyTechnologiesR&DProgramofTianjin(14ZCZDSF00022)

.E-mailsunql@nankai.edu.cn

2016-06-11；退修日期2016-07-19；录用日期2016-09-20； < class="emphasis_bold">网络出版时间

时间：2017-02-200926

www.cnki.net/kcms/detail/11.1929.V.20170220.0926.002.html

国家自然科学基金 (61273138，61573197)； 天津市重点基金 (14JCZDJC39300)； 国家科技支撑计划 (2015BAK06B04)； 天津市科技支撑计划重点项目 (14ZCZDSF00022)

.E-mailsunql@nankai.edu.cn

陶金， 孙青林， 檀盼龙， 等． 翼伞系统在未知风场中的归航控制J． 航空学报,2017,38(5):320523.TAOJ,SUNQL,TANPL,etal.HomingcontrolofparafoilsystemsinunknownwindenvironmentsJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):320523.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0258

V249.1； TP29

A

1000-6893(2017)05-320523-11