径流叶轮直纹叶片的参数化型线自动提取算法

2017-11-20周煜陈思莲杜发荣丁水汀

航空学报 2017年5期

周煜，陈思莲，杜发荣，丁水汀

1.北京航空航天大学交通科学与工程学院，北京 100083 2.新能源汽车高效动力传动与系统控制北京市重点实验室，北京 100083 3.北京航空航天大学能源与动力工程学院，北京 100083

周煜1,2，陈思莲1,2，杜发荣3,*，丁水汀3

流线族(SSL)作为复杂高精度径流式叶轮(RIT)的关键几何元素，对于RIT的建模和气动优化有着非常重要的作用。以RIT的多学科耦合设计为目标，研究了面向型面和特征的联合采集方法以获取RIT表面信息；基于线几何理论，提出了RIT直纹叶片子午流道几何(MS)及直母线矢量(SGVs)的提取方法；探讨了直纹母线矢量的等分算法；研究了可同时控制光顺和逼近程度的叶片型面流线族的拟合方法；建立起以SSL和子午流道几何为参数的径流式叶轮参数化模型，实现对任意RIT样件的SSL自动提取及叶轮的自动参数化建模，通过实例验证了该方法的有效性和可行性。

径流叶轮；直纹叶片；直纹母线矢量；流线族；逆向工程

径流式叶轮(Radial-Inflow Turbomachinery，RIT)如离心压气机叶轮(Centrifugal Compressor Impeller，CCI)是航空发动机、航空用涡轮增压器等旋转机械的关重件，其设计及制造水平对提高机器性能(如压气机效率，压比等)、缩短研发周期和降低制造成本有着重要的影响。随着航空发动机性能要求的提高和航空发动机叶轮设计技术的不断进步，RIT叶片的形状更趋复杂，其精确几何造型[1]成为了RIT加工和气动性能分析的必要前提，造型精度要求也更高。直纹曲面[2]由于其优良的加工性能[3]，被广泛应用于径流叶轮。离心压气机气动性能在很大程度上由直纹叶片型面(吸力面和压力面形状)和子午流道几何(Meridional Section，MS)所决定[4]。因此，精确表达叶片型面和子午流道几何是把握叶轮设计质量的关键因素。

目前，已有的计算机辅助设计技术(Computer-Aided Design，CAD)为复杂几何面的重构提供了多种有效的方法[5]。但由于气动试验与气动仿真分析结果之间存在一定的偏差，CCI的设计一定要根据调整气动仿真分析的相关参数重新进行计算并不断循环此过程，即高质量RIT的设计是几何造型系统、气动优化系统和气动试验系统逐步“迭代”的过程[6]，而目前各系统之间的耦合性较差，因此需要一种能将CAD和CFD建立快速连接的技术来提高设计质量。在气动分析模型建立方面，流线族(SSL)和MS既是径流式叶轮气动设计和几何造型的桥梁和纽带，也可以作为设计输入传递给几何造型系统进行设计和加工。因此，在几何造型中重视径流叶轮的直纹特征，灵活地提取SSL型线和子午流道几何特征对实现几何造型系统和气动优化系统的快速对接有非常重要的作用。

近年来，国内外学者在RIT的直纹特征提取和几何造型等方面做了大量的研究工作。其中，在直纹特征的提取方面，奥地利Pottmann小组[7-8]基于线几何理论将直纹面规划到直线几何范畴, 运用数学方法研究了曲面类型识别方法，为复杂曲面重构问题提供了理论基础；浙江大学柯映林和李岸[9]在旋转特征及母线矢量特征提取方面运用高斯映射、高斯球栅格化、聚类分析等技术手段提出了基于主方向高斯映射的旋转面特征提取方法；Zhang等[10]运用运动学方法将点和线组合构建了直纹曲面，在理论上推导了点—线轨迹和对偶四元素之间的关系；Chailie和Elber[11]采用四维动态规划算法解决直纹面分割和拟合的问题，但在基于散乱点的离散域构建上误差值稳定性不足；Perez-Arribas和Trejo-Vargas[12]讨论了有理直纹面的特征识别和参数化问题，通过曲线的双有理参数变换解决曲面参数化问题；在直纹叶轮可加工性研究方面，大部分成果[13]均集中在如何使不可展直纹面近似可展从而改善加工性能，而RIT叶轮直纹特征在几何造型的重要性往往被忽略。在几何造型方面，Lin等[14]提出以B样条曲线为基础的四边域孔斯曲面构造，该方法构造出的曲面的光顺度高，可加工性好，但曲面与点云的重合度较难保证；Xie等[15]提出在叶片散乱点云的基础上，构造低阶NURBS曲面，再通过逐渐升阶、控制点调整的方式逐步改善曲面的光顺性以及与点云的重合度，得到具有最小能量的高品质曲面。虽然该方法得到的曲面品质较高，能够满足设计要求，但对设计师的要求较高，可实现性较差[16]。

综合以上分析，RIT的系统化设计虽然已经有了长足的发展，但几何造型技术和气动优化技术的耦合性差，设计的自动化程度较低，需要研究设计方法来支持产品设计流程的自动化。本文提出了一种方法可以从RIT的样件中自动提取出SSL和MS并作为参数快速传递给气动优化系统进行气动计算，优化后的SSL和MS反馈给几何系统后能够参数化的生成更新后的模型，这对于高质量叶轮的快速设计具有非常重要的意义。本文的总体技术路线如图1所示。

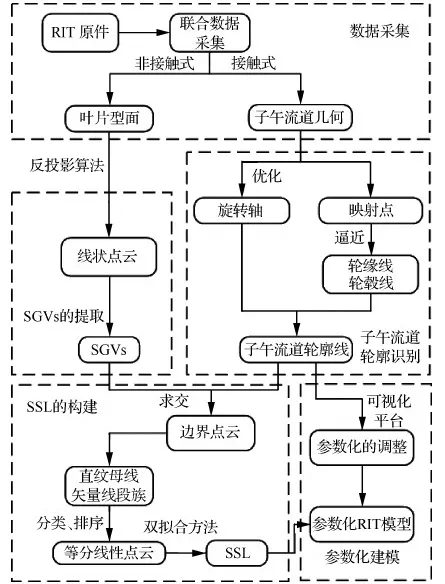
图1 本文的一般框架图 Fig.1 General structure of this paper

1 数据采集与子午轮廓线识别

1.1 点云采集

采用面向型面和特征的联合数据采集方法获取RIT的几何信息，如图2所示。由激光扫描系统Handyscan(TA)采集叶片型面点云数据，分别得到图2中A1和A2所示的高密度的散乱点云数据。由便携式三坐标系统Handyprobe(TB)采集回转柱面、轮毂面和轮缘面的特征点，分别得到图2中B1、B2和B3所示的离散点数据。具体采集设备和数据信息如图3、表1、表2所示。采用基于参考点拓扑关系[17]的坐标系统归一方法对分别由TA和TB采集到的点云数据进行坐标整合。

具体的测量过程是：

步骤1将圆形标记点均匀的粘贴在RIT模型上，标记点的圆心记为mark点，多个mark点构成骨架点点集信息(简称G-group)。

步骤2以G-group为参照，应用便携式光笔三坐标Handyprobe采集RIT样件的特征元素如轮缘轮毂型线等。

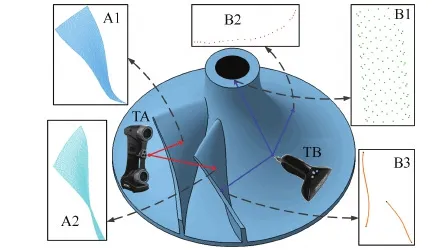
图2 数据采集 Fig.2 Data acquisition

图3 数据采集设备 Fig.3 Devices of data acquisition

表1 Handyscan和Handyprobe的关键参数Table 1 Key parameters of Handyscan and Handyprobe

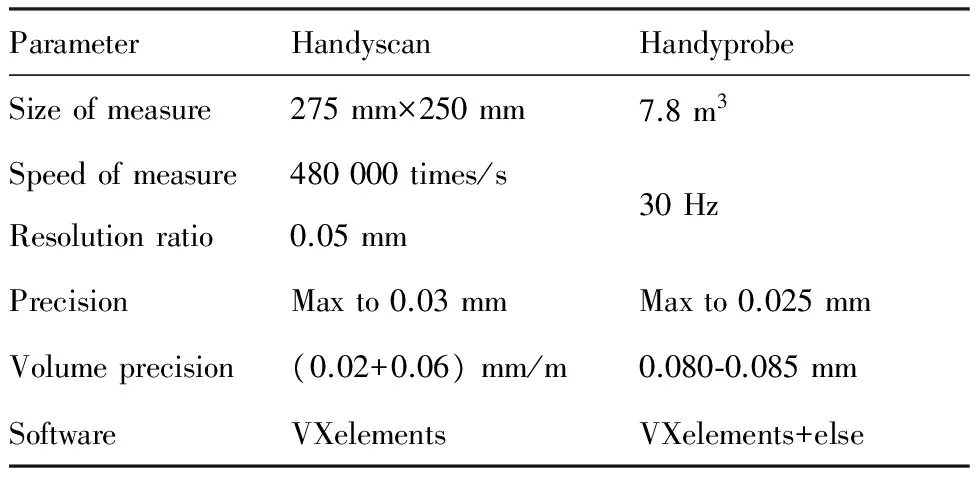
ParameterHandyscanHandyprobeSizeofmeasure275mm×250mm7．8m3SpeedofmeasureResolutionratio480000times/s0．05mm30HzPrecisionMaxto0．03mmMaxto0．025mmVolumeprecision(0．02+0．06)mm/m0．080⁃0．085mmSoftwareVXelementsVXelements+else

步骤3以G-group为参照，应用手持式激光扫描仪Handyscan扫描叶片型面数据。

步骤4基于两组点云数据中相同的G-group，以二次开发代码的形式将自动拼合程序集成在Creaform的软件系统VXelements中，借助该程序完成坐标系的自适应对齐。

鉴于目前的数据采集手段较为丰富，并不限于此一种采集和数据拼合方法，只要保证足够的拼合精度(平均拼合误差不高于0.05 mm)、足够的型面数据点密度(平均点间距不高于0.1 mm)即可。

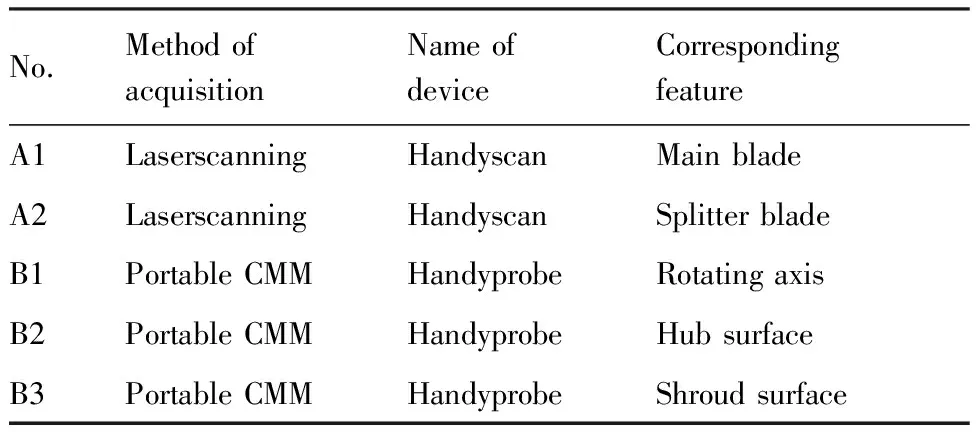
表2 数据采集细节信息Table 2 Detailed information of data acquisition

1.2 轮缘和轮毂母线的提取

对于旋转特征面上每一数据点，过该点且方向矢量为该点处法矢的直线理论上应该和旋转轴共面，此时旋转轴线的提取可以描述为求解约束优化问题，采用Lagrange-Newton法[18]求解方程，即可得到初始旋转轴线。

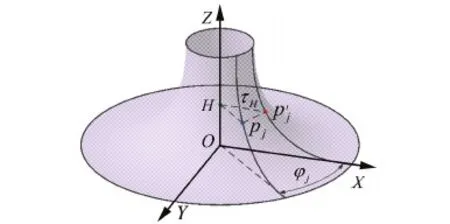
图4 旋转投影原理 Fig.4 Principle of rotation projection

2 直纹母线矢量的提取

直纹母线矢量(Straight Generatrix Vectors，SGVs)[19]是RIT非常重要的几何特征，采用反投影法提取直纹叶片曲面的直纹母线矢量。令大叶片的点云数据为Ct(t=1,2,…,s)，s表示大叶片点云中数据点的个数。反投影算法原理如图5所示，则提取SGVs的步骤为

步骤1构造点云Ct的最小二乘拟合平面，以该平面的法矢量作为Z轴，建立一个三维笛卡尔坐标系。并找出点云Ct在XOY平面投影的最小外接矩形，记为平面S。

步骤2过S平面的几何中心c1可作任一平面Υ11，且Υ11⊥S，则可得Υ11与Ct的截面点云w11。

步骤3对w11进行最小二乘拟合[20]，在平面Υ11上生成直线L11，若拟合误差超过阀值ξ，则根据Υ11绕c1旋转得到平面Υ12生成直线L12。若拟合误差仍超过ξ值，则继续得到平面Υ1j(j=3,…,n)和直线L1j(j=3,…,n)，若直线L1j(j=1,2,…,n)拟合误差小于ξ，则认为L1j(j=1,2,…,n)就是点云Ct中过c1的一条直纹母线矢量。

步骤4Υij与S的交线为li，Lij是根据li得到的直纹母线矢量。计算li的中点hi，则由li⊥hici+1得到ci+1，则同理可得li+1和Li+1,i。

其中，ξ的值由叶片尺寸和直纹母线矢量的数量决定，其建议值为ε/300，ε=|hici+1|是决定SGVs密度的设计阀值。

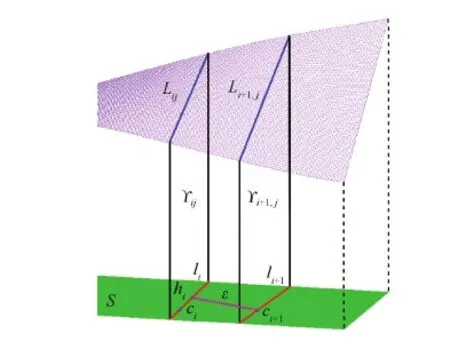
图5 反投影算法原理 Fig.5 Principle of reverse-projection algorithm

3 SSL的构建与RIT的参数化建模

3.1 SSL的提取

分别计算直纹母线矢量族与轮缘面和轮毂面的交点从而生成直纹叶轮的两组边界点。通过直纹母线矢量族与曲面的联合方程，采用数值迭代方法[21]找到所有的边界交点，则通过这些边界点能得出直纹母线矢量的线段族。

设Γi(i=1,2,…,m)为直纹母线矢量线段族，m表示直纹母线矢量线段的条数，给定等分数为Ne，则可计算得到每条直纹母线线段上的等分点ωig(i=1,2,…,m;g=1,2,…,Ne)，将g值相等的等分点依据i值大小进行排序，得到等分线形点云λi(i=1,2,…,Ne)，如图6所示。

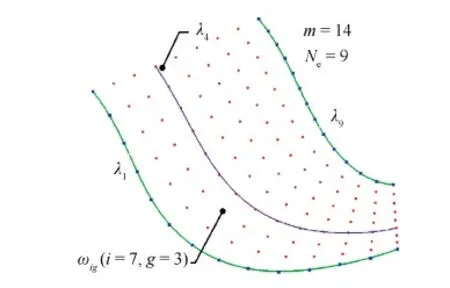
图6 等分线性特征点云 Fig.6 Uniform partition of line point cloud

采用二次拟合方法，即先利用插值的方法构造一条基准曲线，再构造B样条曲线逼近基准曲线，从而生成SSL。算法具体为

步骤1给定m+1个数据点q0,q1,…，qm，寻找一条k阶B样条曲线s(u)，使得s(u)通过或逼近这些数据点。

步骤2采用局部插值法，选用G1连续的三阶B样条曲线构造基准曲线t(u)。

步骤3采用最佳平方逼近方法逼近基准曲线，通过求解线性方程组来求解控制顶点以得到逼近曲线。给出目标函数：

(3)

为了提高拟合曲线的光顺程度，给出光顺目标函数：

(4)

式中：α、β为可控光顺近程度的权重因子。

Qa和Qs共同构成了逼近曲线的目标函数：

Q=γQa+Qs

(5)

式中：γ为曲线逼近程度的权重因子。

步骤4当α、β、γ值确定后，可得到一个以控制顶点为变量的优化系统，只需要令Q关于控制顶点D=[di](di表示第i个控制顶点)的n+1个偏导数为0，则得到一个关于D=[di]的线性方程组：WD=G，其中，

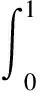
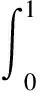
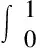
根据B样条基的差商定义[22]，可计算Wi,j和G，然后应用高斯消去法求解线性方程组WD=G，即可得到拟合曲线的控制顶点。

3.2 参数化模型的构建

SSL与直纹母线矢量族构成了RIT叶片的两

条参数曲线，通过参数化建模的方法生成RIT叶片的蒙皮曲面。所有叶片以回转轴为中心周向均布，叶片曲面的参数化是RIT参数化建模的必要条件。

以RIT叶轮为例，采用前述的方法对TA采集到的叶片子午流道几何中特征数据点进行B样条曲线拟合，分别生成轮缘型线与轮毂型线，分别绕回转轴旋转即可得到轮缘面和轮毂面，如图7 中的R1和R2所示，对采集到的RIT外轮廓圆柱点云进行圆柱特征识别，生成RIT的外廓圆柱面，如图中R3所示。由R1、R2、R3及前述方法得到的大叶片蒙皮曲面Y1和小叶片蒙皮曲面Y2，通过求交、裁剪、倒圆角等算法共同构建参数化RIT模型。图8所示为基于本文算法在Visual Studio平台中建立参数化RIT，该系统具备模型参数化修改和自动更新的能力。

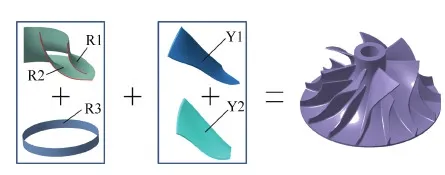
图7 RIT的参数化建模 Fig.7 Parameterized modeling for RIT

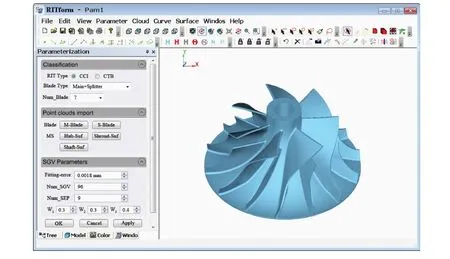
图8 基于RIT平台的CCI设计 Fig.8 Design of CCI based on RIT platform

4 实例验证

如图9所示，实验工件高为38.45 mm，外径为37.4 mm且大小叶片各有7片的CCI，以下出现的实验结果均在电脑型号为Intel Core i7 2.7 GHz CPU+16 RAM 和NVIDIA Quadro K2100M GPU中输出。其中，图9(a)所示为实验工件；图9(b)为使用本文方法所采集的点云，C1和C2分别为叶片吸力面和压力面高密度的线扫描点云数据，D1、D2和D3分别为转柱面、轮毂面和轮缘面特征点的离散点云数据；图9(c)为建立的参数化模型；图9(d)为使用本文方法所提取的大叶片的直纹母线矢量；图9(e)为小叶片提取的直纹母线矢量；图9(f)为使用本文方法所提取的大叶片的SSL；图9(g)为小叶片提取的SSL；图9(h)为大叶轮曲面与点云的重合度分析，其平均误差数值为0.009 2 mm。

基于本算法实例验证的相关参数如表3所示。

SSL、MS以及参数化模型能被传递给CFD解算器进行气动计算[23]。规定气动参数和配置的CCI在设计速度为82 000 r/min状态下的运行特性如图10～图12所示：静态压力分布如图10所示；相对马赫数分布如图11所示；流线族分布如图12所示。由气动计算结果可对轮缘线及轮毂线进行优化设计，优化后的轮缘线和轮毂线反馈给几何造型系统，RIT的几何模型可被参数化更新，如图13所示。

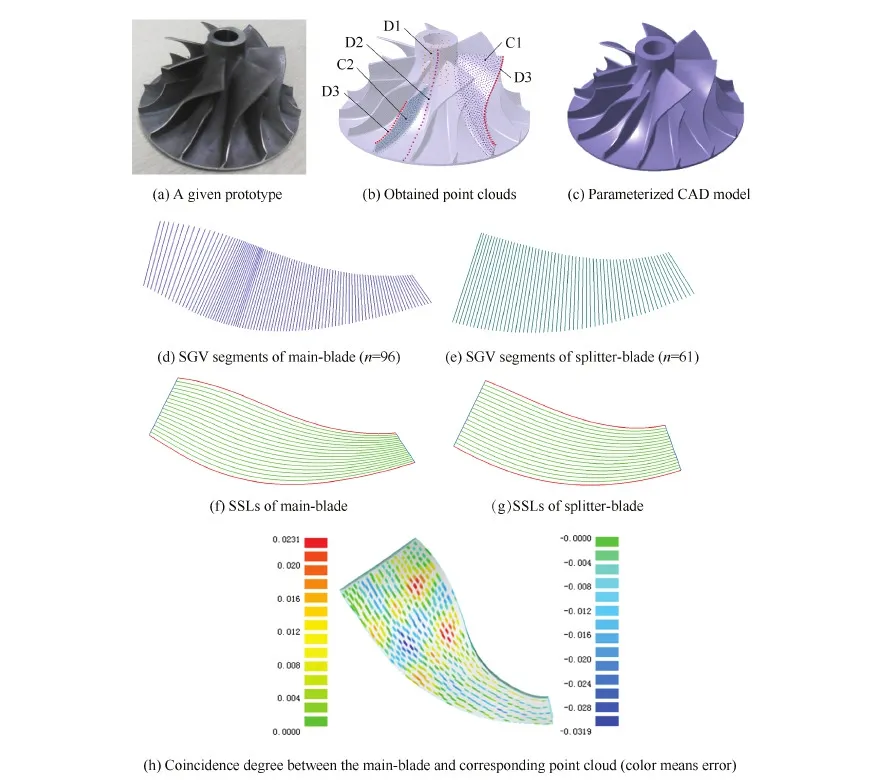
图9 基于本文算法的验证实例 Fig.9 A demonstrated example based on proposed algorithm

表3 本算法验证实例的参数Table 3 Parameters of proposed algorithm based on the above example

TypesofRITTypesofbladeNumberofbladesNumberofpointsSGVfittingerrorδ/mmNumberofSGVsAmountofequantpointsWeightfactorOperationtime/sαβγMSBladeCCIMain⁃blade7857960．00189690．300．300．40Splitter⁃blade7641370．00186190．300．300．400．221．180．75

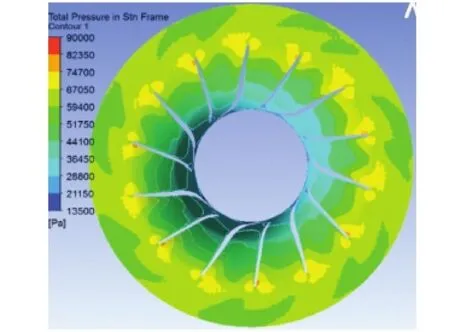
图10 静态压力分布 Fig.10 Static pressure distribution

图11 相对马赫数分布 Fig.11 Relative Mach-number distribution

图12 流线族分布 Fig.12 Streamlines distribution

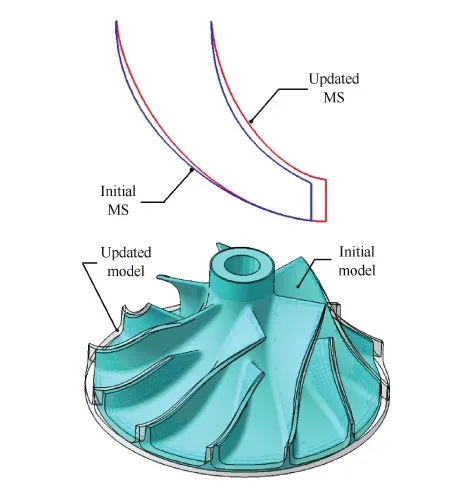
图13 原始与更新后的特征和模型的变化 Fig.13 Difference of feature and model between initial and updated

5 结论

1) 提出了一种径流直纹叶轮叶片型面流线族(SSL)和子午流道几何(MS)特征自动提取算法及径流叶轮参数化建模方法。该方法能从径流叶轮样件中自动提取SSL和MS，同时能使模型随着SSL和MS参数的修改而参数化更新。

2) 自动提取的SSL和MS作为RIT多学科耦合设计的桥梁和纽带，通用于CAD/CFD及AT系统中。

3) 该方法使得气动优化和几何造型的设计环节联系紧密，提高了RIT设计的自动化程度，为径流直纹叶轮的快速化、集成化设计提供了可行性，也为具有此类特征的复杂工件的设计和快速制造提供了理论依据。

4) 提出的方法虽然能很好地应用于单值直纹面叶轮或具有类似曲面特征的叶轮，但是在处理具有复杂数学模型和几何特征的叶轮上仍然存在不足。因此，扩展模型的适用性，也是未来的研究方向。

[1] WALTHER B, NADARAJAH S. Optimum shape design for multirow turbomachinery configurations using a discrete adjoint approach and an efficient radial basis function deformation scheme for complex multiblock grids[J]. Journal of Turbomachinery,2015, 137(8): 081006-1-081006-20.

[2] LIANG Q, WANG Y Z, FU H Y. Cutting path planning for ruled surface impellers[J]. Chinese Journal of Aeronautics, 2008, 21(5): 462-471.

[3] LI M Y, LIU X L, JIA D K. Interpolation using non-uniform rational B-spline for the smooth milling of ruled-surface impeller blades[J]. Proceedings of the Institution of Mechanical Engineers, 2015, 229(7): 1118-1130.

[4] XU C, AMANO R S. Meridional considerations of the centrifugal compressor development[J]. International Journal of Rotating Machinery, 2012, 2012(9): 1-11.

[5] TEODOR M. Impeller design using CAD techniques and conformal mapping method[J]. Centrifugal Pumps, 2012, 24(2): 33-64.

[6] KIM J H, CHOI J H, HUSAIN A. Multi-objective optimization of a centrifugal compressor impeller through evolutionary algorithms[J]. Journal of Power and Energy, 2010, 224(5): 711-721.

[7] POTTMANN H, PETERNELL M, RAVANI B. An introduction to line geometry with applications[J] .Computer-Aided Design, 1999, 31(1): 3-16.

[8] POTTMANN H, WALLNER J. Computational line geometry[M]. 2001.

[9] 柯映林，李岸．基于主方向高斯映射的旋转面特征提取[J]．浙江大学学报(工学版), 2006， 40(6)： 942-946.

KE Y L, LI A. Rotational surface extraction based on principal direction Gaussian image from point cloud[J]. Journal of Zhejiang University (Engineering Science), 2006， 40(6)：942-946 (in Chinese).

[10] ZHANG X M, ZHU L M, DING H. Kinematic generation of ruled surface based on rational motion of point-line[J]. Science China, 2012, 55(1): 62-71.

[11] CHAILIE C W, ELBER G. Multi-dimensional dynamic programming in ruled surface fitting[J]. Computer-Aided Design, 2014, 51(6): 39-49.

[12] PEREZ-ARRIBAS F, TREJO-VARGAS I. Computer-aided design of horizontal axis turbine blades[J]. Renewable Energy, 2012, 44(8): 252-260.

[13] BI Q Z, ZHU L M, WANG Y H. Analytical envelope surface representation of a conical cutter undergoing rational motion[J]. International Journal of Advanced Manufacturing, 2010, 47(5): 719-730.

[14] LIN K Y, HUANG C Y, LAI J Y, et al. Automatic reconstruction of B-spline surfaces with constrained boundaries[J]. Computers & Industrial Engineering, 2012, 62(1): 226-244.

[15] XIE W C, ZOU X F, YANG J D, et al. Iteration and optimization scheme for the reconstruction of 3D surfaces based on non-uniform rational B-splines[J]. Computer-Aided Design, 2012, 44(11): 1127-1140.

[16] AKEMI G, ANDRÉS I. Particle swarm optimization for non-uniform rational B-spline surface reconstruction from clouds of 3D data points[J]. Information Sciences, 2012， 192(6): 174-192.

[17] ALAN C L, CHANG H C. Automatic 3D measuring system for optical scanning of axial fan blades[J]. International Journal of Advanced Manufacturing, 2011, 57(4): 701-717.

[18] LU D J, LII K S, WANG Y. The formulae and algorithms for Lagrange-power basis transformation and Lagrange-Newton transformation[J]. Applied Mathematics and Computation, 2015, 32(5): 1-20.

[19] LAURENT B, MOHAMED E, ANDRE G. A computa tional study of ruled surfaces[J]. Journal of Symbolic Computation, 2009, 44(3): 232-241.

[20] ARANDIGA F, NOGUERA J J. Reconstructions that combine interpolation with least squares fitting[J]. Applied Numerical Mathematics, 2015, 97(11): 30-41.

[21] DARIO A, BINI A M. Computing curve intersection by means of simultaneous iterations[J]. Numerical Algorithms, 2006, 43(2): 151-175.

[22] WANG M H, YUE S. Error prediction and compensa-tion based on interference-free tool paths in blade milling[J]. International Journal of Advanced Manufacturing, 2014, 71(5): 1309-1318.

[23] ZHOU X, ZHANG Y X, JI Z L. The optimal hydraulic design of centrifugal impeller using genetic algorithm with BVF[J]. International Journal of Rotating Machinery, 2014： 845302.

(责任编辑：李世秋)

URL：www.cnki.net/kcms/detail/11.1929.V.20161019.1313.002.html

Automaticextractionalgorithmofparameterizedstreamlinesfromaradial-inflowturbomachineryruledblade

ZHOUYu1,2,CHENSilian1,2,DUFarong3,*,DINGShuiting3

1.SchoolofTransportationScienceandEngineering,BeihangUniversity,Beijing100083,China2.BeijingKeyLaboratoryforHigh-efficientPowerTransmissionandSystemControlofNewEnergyResourceVehicle,Beijing100083，China3.SchoolofEnergyandPowerEngineering,BeihangUniversity,Beijing100083，China

Asetofstreamlines(SSL),asasignificantgeometricelementincomplexradial-inflowturbomachinery(RIT)withhighprecision,playsavitalroleinmodelingandaerodynamicoptimizationofRIT.AimedatmultidisciplinarydesignofRIT,wedevelopanintegratedacquisitionmethodorientedtowardstheprofileandcharacteristicsofRITtoobtainthesurfaceinformationofRIT.Anextractionmethodofthemeridionalsection(MS)andstraightgeneratrixvectors(SGVs)oftheRITwiththeruledsurfaceisproposedbasedonlinegeometrytheory.ThedivisionalgorithmofSGVsisanlayzed.AmethodforSSLfittingispresentedtocontrolboththesmoothingandapproximationdegreeofthebladesurface.AparametricmodelofRITisestablishedbyusingSSLandMSasparameterstorealizeautomaticextractionofSSLfromarbitraryRITprototypeandautomaticparametricmodelingoftheimpeller.Acaseexampleisgiventodemonstratetheeffectivenessoftheproposedstrategy.

radial-inflowturbomachinery(RIT);ruledblade;straightgeneratrixvector;setofstreamlines(SSL);reverseengineering

2016-07-07；Revised2016-07-18；Accepted2016-09-05；Publishedonline2016-10-191313

NationalNaturalScienceFoundationofChina(51205015)

.E-maildufrong@hotmail.com

2016-07-07；退修日期2016-07-18；录用日期2016-09-05； < class="emphasis_bold">网络出版时间

时间：2016-10-191313

www.cnki.net/kcms/detail/11.1929.V.20161019.1313.002.html

国家自然科学基金(51205015)

.E-maildufrong@hotmail.com

周煜，陈思莲，杜发荣，等. 径流叶轮直纹叶片的参数化型线自动提取算法J. 航空学报，2017,38(5):420592.ZHOUY，CHENSL，DUFR，etal.Automaticextractionalgorithmofparameterizedstreamlinesfromaradial-inflowturbomachineryruledbladeJ.ActaAeronauticaetAstronauticaSinica，2017,38(5):420592.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0250

V232.4

1000-6893(2017)05-420592-09