近场试验条件对二维干涉仪测向系统的影响

李 琳，居 易

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

近场试验条件对二维干涉仪测向系统的影响

李 琳，居 易

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

基于干涉仪测向原理，分析了干涉仪测向系统近场试验验证时产生较大误差的2种原因，仿真给出了2种条件下二维干涉仪的测向结果受辐射源距离以及转台旋转角度的影响，推导出天线位置偏心时的测向误差校正公式，提出用仿真结果对试验中由于球面传播产生的测角误差进行补偿的方法。

干涉仪测向；误差；偏心；球面传播

0 引 言

干涉仪测向技术自出现以来就以其测向精度高、实时性好、成本低等优点被广泛应用于电子侦察领域。干涉仪测向的实质是利用无线电波在测向基线上形成的相位差来确定来波方向[1]。而二维干涉仪可同时对来波的方位角和俯仰角进行测向。

干涉仪测向系统使用前需通过试验验证和通道间相位差标校，在测试试验过程中，如果忽略试验条件近场特性而使相位标校引入较大误差，将严重影响测向系统应用时测向的正确性。

1 二维单基线测向原理

如图1所示的三元阵，阵元0，1的连接线与阵元0，2的连接线垂直，建立图1所示的坐标系。其中，θv为来波的俯仰角，θh为来波的方位角，d为单基线长度。

图1 二维单基线原理说明图

俯仰角和方位角的计算公式如下：

(1)

(2)

式中：φx为0，1基线相位差；φz为0，2基线相位差。

二维多基线干涉仪测向是利用多基线解模糊得到单基线相位差后经过式(1)、式(2)计算得到测向结果，多基线解模糊算法比较复杂，本文不再赘述。

2 近场试验条件下测向误差原因分析

2.1 天线阵安装位置偏心

测向系统试验时，是将接收天线阵安装在二维测试转台上，使用固定模拟目标向天线阵发射信号，以验证测向的准确性[2]。很多情况下，由于天线结构和测试转台结构的限制，天线阵安装位置会偏离二维测试转台的中心，使得同一目标对于二者有不同的方向，此时用测试转台旋转角度来衡量干涉仪测向结果会出现一定的误差。

下面以某二维L型天线阵为例，讨论天线安装位置偏心时，测向结果的误差。该L型天线阵在转台上的安装位置如图2所示，水平天线阵与转台的俯仰转轴平行。天线阵安装在与转台相交的斜面上。其中，以转台俯仰转轴为x轴，水平转轴为z轴，转台中心为原点O建立Oxyz坐标系，Otxtytzt坐标系是将Oxyz坐标系的原点O平移到L型天线阵顶点Ot得到的，那么可以在此基础上计算目标在两坐标系下的俯仰角和方位角的误差。

图2 偏心示意图

可以将测试时二维转台的旋转看作坐标系Oxyz的旋转。假设有一固定辐射源A，在Oxyz坐标系中坐标为(x,y,z)，试验时转台先绕x轴顺时针旋转角度α(垂直旋转角度)，再绕z轴旋转γ(水平旋转角度)，然后平移向量t，得到Otxtytzt坐标系，如图3所示。

图3 坐标系转换示意图

那么，固定位置辐射源在Otxtytzt坐标系中的坐标(xt,yt,zt)为：

(3)

(4)

(5)

式中：Aα，Aγ分别为绕x轴旋转角度α，绕z轴旋转角度γ的坐标系旋转矩阵；t为转台中心到L型天线阵顶点的向量OOt。

辐射源在两坐标系中的俯仰角和方位角为：

θh=arctan(x/y)

(6)

θv=arcsin(z/sqrt(x2+y2+z2))

(7)

(8)

(9)

以转台坐标系的测向结果作基准，俯仰角和方位角的误差可以表示为：

(10)

(11)

对图2所示的天线阵偏心所产生的测向误差进行仿真分析。假设相对于Oxyz坐标系，L型天线阵顶点坐标为(0.2,0.6,1.2)m，固定辐射源的初始坐标为(0.2,0.6,ly)m。选择ly=50,α,γ从-60°变化到60°，变化间隔为1°，仿真得到的测角误差如图4、图5所示。

图4 俯仰角误差

图5 方位角误差

观察俯仰角和方位角测角误差随转台的垂直旋转角度和水平旋转角度的变化，可以看出|e|最大值接近1.5°。图中分层规律显示，垂直旋转角度主要影响俯仰角，水平旋转角度主要影响方位角。

选择α=18°，γ=-55°，ly从10 m增加到100 m，俯仰角和方位角的误差如图6所示。俯仰角和方位角的误差随辐射源的距离增大而减小。并且在一定范围内，距离减小，误差急剧增大。距离为10 m时，俯仰角误差甚至达到7°。

图6 辐射源距离对俯仰角和方位角的影响

综上分析，由于天线安装位置的偏心，使得测向系统的测向结果与转台坐标系的定向结果之间存在误差。

综合图4、图5、图6，该误差在辐射源距离50 m时还能达到接近1.5°，辐射源距离越近，误差越大。可见在内场试验时，偏心对测向结果有相当大的影响，如果不对偏心的影响进行分析和校正，简单地以转台旋转角度衡量测向结果，会严重影响对测向系统的试验验证。

2.2 近场电磁波球面传播的影响

由辐射源发出的电波是球面波，到接收天线的距离很大(与波长相比)时，可以近似认为平面波[3]，干涉仪测向系统是在这一理论基础上建立的。但试验场受空间限制，辐射源距离一般不满足近似平面波条件。

以一维单基线两阵元为例，说明电磁波的球面传播模式下阵元间相位差与近似平面波传播时相位差的计算方式不同，如图7所示，O为辐射源，A、B为接收阵元。

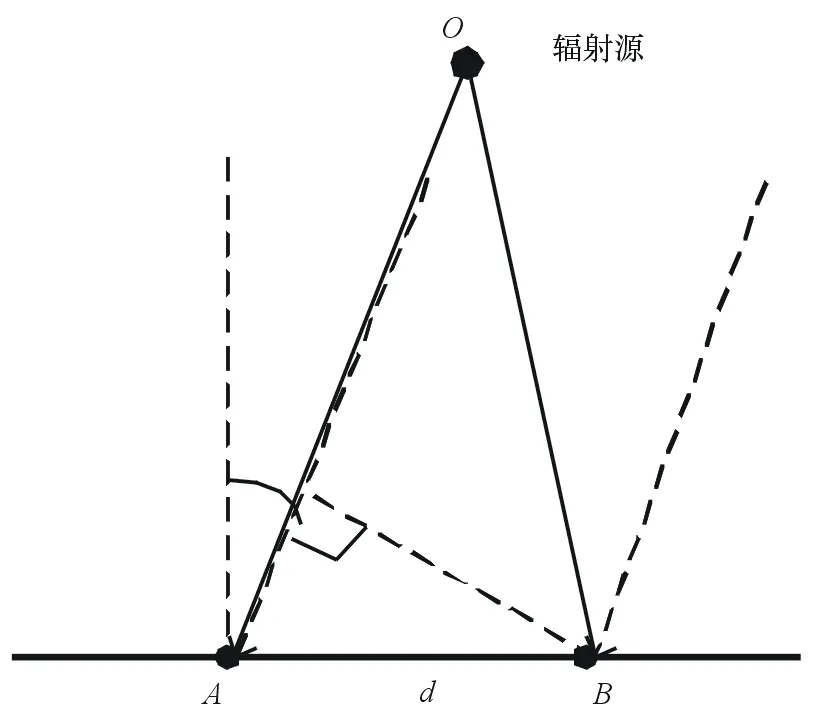
图7 一维单基线测向说明图

辐射源距离远大于阵元间距d时，电磁波近似为平面波传播，A，B接收到的信号波达角近似相同(如图7虚线所示)，波达角为θ，波程差为dsinθ，相位差φ为：

(12)

而球面波传播时，波程差为OA-OB(如图7实线所示)，相位差φ为：

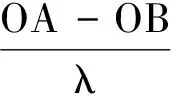
(13)

干涉仪测向系统是在式(12)的基础上计算波达角的。但是近场试验时，实际相位差的理论值为式(13)的结果，最终造成测向误差。

仍以图2所示的天线阵为例，采用适当的基线比可得到各接收阵元的坐标，通过式(13)计算出阵元间相位差，经过适当的解模糊算法，从而模拟出干涉仪测向系统的测角结果，与通过坐标计算得到的方位角和俯仰角的精确结果进行对比分析。因为考虑的是测向系统本身的测向误差，所以仅在Otxtytzt坐标系下分析。俯仰角和方位角的测角误差为：

(14)

(15)

式中：θhc,θvc为干涉仪测向系统得到的方位角和俯仰角。

固定辐射源的初始坐标为(0,0,ly)。ly分别选20，35，50,α,γ从-60°变化到60°，变化间隔为1°。仿真的结果如图8、图9所示。

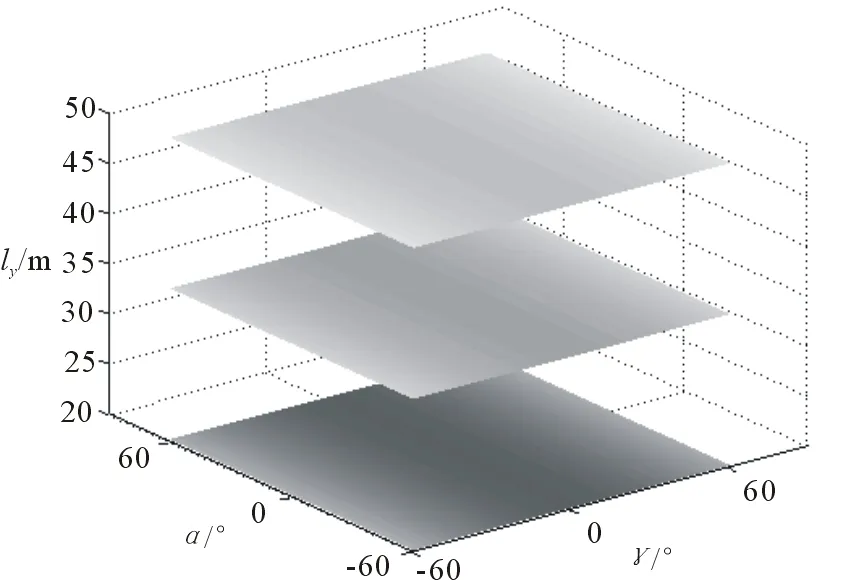
图8 俯仰角测角误差

图9 方位角测角误差

从图中可以看出，辐射源的距离和转台的旋转角度，都对测角误差有影响。方位角测角误差受距离影响较大，而俯仰角误差也受距离影响，两者都随着距离的增大而减小。

为了进一步分析这3个因素的影响，以方位角误差为例，转台旋转角度选取(45°,45°)和(60°,60°)，得到图10。

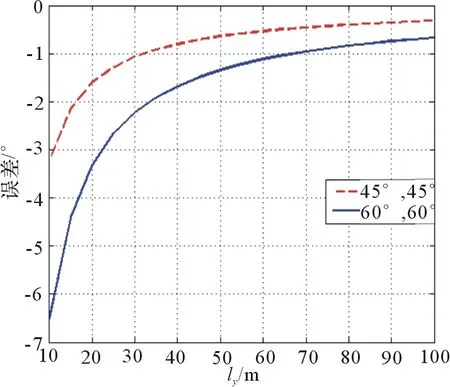
图10 球面传播距离的影响

图10显示，距离对测角结果影响很大。(45°,45°)的情况，距离近时，误差可以达到3°；距离增大到60 m，误差才减小到0.5°以内。由图9也可以看出，仿真选取的转台旋转角度(45°,45°)并不是最恶劣的情况，若是旋转角度选取更恶劣的情况，会造成同一距离产生的误差相对增大，如图10中实线所示。

旋转角度选择(45°,45°)，相位噪声服从均值为0、方差为0.05×2π的正态分布，采样间隔为1 s，观测10 s，仿真得到方位角误差，并用图10中的结果对其进行校正，结果如图11所示。

在电磁波实际以球面传播时，不论是距离还是转台旋转角度，都对测向结果产生较大的误差，这种影响是不能忽略的，如果没有考虑到近场球面传播时的这类误差，也会对测向系统的试验验证造成严重影响。

图11 方位角误差校正结果

3 结束语

干涉仪测向系统产生误差的原因有很多[4]，本文仅分析了由于试验时的近场条件，二维干涉仪测向系统产生测向误差的相关因素，仿真了产生的测角误差，得出以下结论：

(1) 天线安装位置偏心会使干涉仪测向结果与转台旋转结果产生较大偏差，在试验时可利用式(10)、式(11)进行校正。

(2) 试验不满足远场条件，会使干涉仪测向系统本身的测角结果产生很大误差，可尽可能地增大辐射源的距离、减小转台旋转范围来减小误差。

(3) 受试验场空间限制，辐射源距离无法增大时，可以对不同距离、不同转台旋转角度的测角误差进行仿真计算，形成完备的测角误差数据库，对干涉仪测向结果进行校正，此方法有待于进一步仿真验证。

[1] 肖秀丽.干涉仪测向原理[J].中国无线电,2006(5):43-49.

[2] 王晨晨,房景仕.二维测试转台偏心误差修正技术研究[J].自动化与信息工程,2013,34(4):11-15.

[3] 薛建彬.现代通信技术[M].北京:北京理工大学出版社,2013.

[4] 张娟,刘恒,何冠良.干涉仪测向系统相位误差校准方法[J].雷达与对抗,2014,34(3):23-26.

InfluenceofNear-fieldTestConditionsonTwo-dimensionalInterferometerDirection-findingSystem

LI Lin,JU Yi

(The 723 Institute of CSIC,Yangzhou 225001,China)

Based on the principle of interferometer direction-finding,this paper analyzes two reasons of measurement error when the interferometer direction-finding system is in near-field test,simulates the impact of emitter distance and rotation angle of the turntable on 2D interferometer direction-finding results under the two conditions,educes the direction-finding error correction formula when the antenna position is off-center,proposes the method using the simulation result to compensate the angle measurement error caused by the spherical propagation in tests.

interferometer direction-finding;error;off-center;spherical propagation

TN971

A

CN32-1413(2017)05-0044-04

10.16426/j.cnki.jcdzdk.2017.05.009

2017-09-06