IFF模式5高精度测频方法研究

詹银芳，王姜铂

(中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033)

IFF模式5高精度测频方法研究

詹银芳，王姜铂

(中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033)

基于敌我识别(IFF)模式5询问信号，在采样点数较少、不能增加点数情况下研究了提高测频精度的方法，无噪声与加入高斯白噪声的情况下，采用快速傅里叶变换(FFT)测频粗估计信号载波频率，利用谱峰位置插值校正的方式减小频率估计误差，提高测频精度。仿真结果表明该方法简单，能够有效提高测频精度。

敌我识别；测频；快速傅里叶变换；精度

0 引 言

敌我识别(IFF)是对目标敌我属性进行识别，可以提高作战的准确性、灵活性与有效性。目前，各国都在研制MARK XIIA，它是新一代敌我识别系统，其核心是模式5。它具有改进的询问、应答识别方式，采用了扩频技术，提高了系统的抗干扰能力。Mode 5信号频率测量是敌我识别的重要环节，有时需要在短时间内对信号的频率进行精确估计。但在频谱监测过程中，截获信号的频率是未知的，所以需要通过信号的频谱获取载频信息。用于载频估计的方法有很多，如采集更多的数据和补零，这2个方法都增加计算量，快速傅里叶变换 (FFT)谱连续细化傅里叶变换分析法在频率成分泄漏影响大的情况下会估算不准确。考虑工程实现性强与频率估计的准确性，本文采用对Mode 5信号平方谱做FFT粗估计信号的频率，再根据谱峰位置插值法校正信号频谱，得到频率的精确估计值。通过仿真表明，实现信号测频精度的提高是完全可行的，可在工程中广泛应用。

1 IFF模式5信号分析

1.1 Mode 5信号

IFF模式5有4级工作模式，其中Level 1、Level 2询问信号的格式如图1所示，Level 3和Level 4的技术规范还投有完全定义。其中，P1～P4为4个同步脉冲，变化量由加密机S1～S3分别产生；L1～L2为2个旁瓣抑制脉冲；D1～D11为11个数据脉冲，经过(11,9,1)RS编码得到44 bit数据信息。模式5询问脉冲信号采用最小频移键控(MSK)调制[1]，码速率是16 Mb/s。

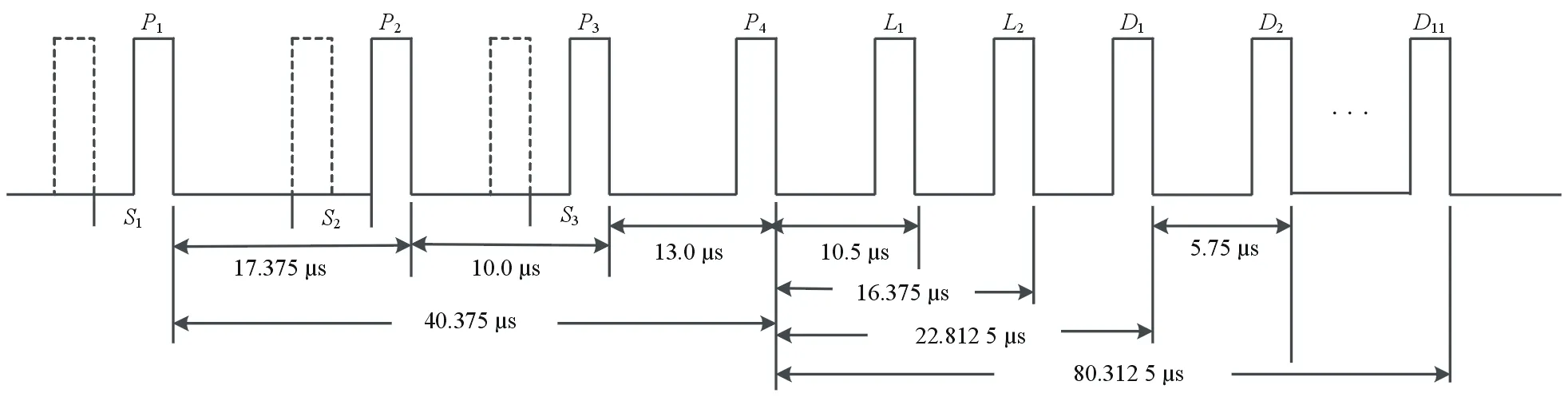
图1 IFF Mode 5询问信号格式

模式5 Level1 和 Level2 询问信号脉冲持续时间为1 μs。同步脉冲P1～P4用于询问模式识别，P1～P4的间隔可变，变化量由加密机产生，分别是S1、S2和S3，旁瓣抑制脉冲L1、L2用于抑制询问旁瓣。数据脉冲D1～D11，每个数据脉冲含有4 bit 信息，11 个数据脉冲共44 bit 信息，它由加密机产生36 bit 加密询问信息，经过(11,9)RS 编码后得到。询问脉冲经过扩频和MSK 调制后发射出去，询问信号频率1 030 MHz。

1.2 Mode 5信号载波频率

Mode 5询问信号调制后的MSK频谱可以直观地反映信号功率在频率上的分布情况，频谱会产生很大的直流分量，需要做去直流处理。MSK信号倍频后调制指数变为 1，在平方谱中会出现2根明显的离散谱线，即为二倍传号频率2fH和二倍空号频率2fL。根据MSK信号特征，很容易得到载波频率fc和码速率fp，与2根离散谱线直接关系为：

(1)

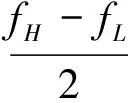
(2)

在一定信噪比条件下，当2个频率成份非常接近时，由于彼此的泄漏对对方的影响很大，会使得次大值趋近于噪声电平，故不能用上面的式子求载波频率fc，这时可以使用下面式子进行计算:

(3)

式中：fmax为平方谱中谱线最大值的频率。

2 测频方法分析

Mode 5 MSK信号经过采样，对信号平方谱做快速傅里叶变换 (FFT)，粗估计信号的频率，再根据谱峰位置插值法校正信号频谱，得到频率的精确估计值。

2.1 快速傅里叶变换测频分析

Mode 5 MSK的信号表达式为[2]：

(4)

式中：fc为载波频率；Tb为码元周期；φk为第k个码元的相位常数。

信号加噪声后混合波形为：

x(t)=s(t)+z(t)

(5)

假设信号采样率为fs，码元速率为ps，采样点数为N，经过数字化采样并对信号平方谱进行FFT处理后，信号的频率分辨率为：

Δf=fs/N

(6)

根据谱线的最大值估计信号频率，若信号频率正好在谱线上，则频率测量结果是精确的。但大多数情况，信号频率在2根谱线之间，由最大值谱线位置反映的频率存在误差，最大测频误差为Δf/2[3]。

对MSK信号使用FFT算法的处理后，N点信号的离散谱如图2所示。根据谱线的最大值估计信号频率，若信号频率正好在谱线上，则频率测量结果是精确的。但发现大多数情况下，信号频率在2根谱线之间，很少位于FFT频率谱线上。从图中可以看出信号谱的峰值位于x=7和x=8 FFT频率谱线之间，发现频谱幅度最大的点更靠近x=7的频率谱线，故信号位于x=7和x=7.5频率单元中心。此时，由最大值谱线位置反映出频率存在误差，最大测频误差为Δf/2。

图2 N点信号的离散谱

从式(6)看出，可以通过增加点数或者降低采样率来提高测频精度，假设采集4N个时域信号采样点并进行4N个点的FFT，得到频率单元间距为fs/4N的频谱，或者对原N点时间采样点补充3N个0值采样点，如图3所示。在图中，频谱峰值位于x=26，估计信号的频率与信号的频率分辨率如下：

(7)

(8)

图3 4N点信号的离散谱

采集更多的数据和补零这2个方法都会增加计算量，而且在有噪声时，补零也不能改善信噪比。在低信噪比下，定位频谱峰值点可能出现错误，造成测频误差增大。降低采样率使得信号频率分析范围降低，在实际采集MSK信号时，信号长度和采样率会受到限制。故需要对FFT粗测得的载频采用一种计算简单的频率校正算法，进一步提高测频精度。

2.2 谱峰位置插值法分析

谱峰位置插值是利用频谱峰值两侧的2根FFT谱线，对FFT最大谱线位置进行校正，根据修正频率变量的方程求解得到修正频率值，以实现对信号频率更高精度的估计。

IFF模式5询问信号是脉内带调制的复杂信号类型，可以采用各种信号处理方法转化为普通正弦波信号。

仿真模拟一个MSK信号进行FFT后，频率是离散的谱线，其轮廓为辛格函数[4]，如图4所示。可以看出，信号的中心频率fz与辛格函数的最大值不一致，真实频率可以使用下面式子估计[5]：

fr=fz±real(δ)

(9)

(10)

式中：fz为最大幅度A(fz)对应的频率索引；A(fz+1)和A(fz-1)为频谱峰值两边的采样值;δ为校正因子。

若频率次大值在最大值的右边，频率的精确值fr位置应该在fz与fz+1之间，更靠近fz，式子取-号；若频率次大值在最大值的左边，则频率的精确值fr位置应该在fz与fz-1之间，更靠近fz，式子取+号。

在进行谱峰位置搜索时，找出最大峰值与次大峰值的位置就可以计算信号基于索引坐标的频率fr，并将其用于下式来估计频谱峰值频率:

(11)

图4 谱峰位置插值频谱图

通过上述可知，在进行谱峰位置搜索时，只需要找出频谱最高峰和次高峰的位置，通过计算就可以得出较精确的信号频率。这个频谱峰值估计算法很简洁且准确，不需要对原信号加窗。

3 仿真验证分析

为验证上一章的方法，下面进行仿真分析。采样率为fs=500 MHz，采样点数N=500，码速率ps=16 MHz，模拟载波频率为130 MHz，加入10 dB信噪比高斯白噪声。

在未加入噪声与加入高斯白噪声2种情况下，模拟产生IFF模式5 MSK信号，对信号的频谱做直流处理去除直流分量，低通滤波后将频谱做平方，并进行FFT运算。仿真结果如图5所示。

图5 未加入噪声MSK平方谱和加入噪声后MSK平方谱

由图5可知，对FFT结果求最大值，粗测1次得到载波频率均为130.5 MHz,测频误差为0.5 MHz，再根据平方谱峰值位置插值法原理，进一步估计载频。使用谱峰值位置法后，测量获得的载波频率未加入噪声与加入高斯白噪声2种情况下，测频误差分别为10.7 kHz、65 kHz。

以采样率为fs=500 MHz，采样点数N=500，码速率ps=16 MHz，模拟不同的载波频率(为130～140 MHz，间隔0.1 MHz)，加入10 dB信噪比高斯白噪声,连续101次测频，未加噪声与加噪声的测频误差如图6所示。

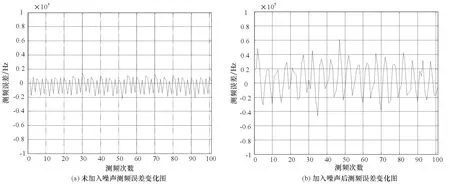
图6 未加入噪声测频误差变化图和加入噪声后测频误差变化图

由图6可知,未加入噪声时最大测频误差不超过22 kHz，均方误差为11.4 kHz；加入噪声后最大测频误差不超过62 kHz，均方误差为23.4 kHz。测频误差大大降低。

以采样率为fs=500 MHz，采样点数N=500，码速率ps=16 MHz，模拟相同载波频率(为130 MHz)，加入10 dB信噪比高斯白噪声,连续101次测频，未加噪声与加噪声的测频误差如图7所示。

由图7可知,未加入噪声时最大测频误差不超过42 kHz，均方误差为11.9 kHz；加入噪声后最大测频误差不超过60 kHz，均方误差为16.8 kHz。测频误差大大降低。

以采样率为fs=1 000 MHz，采样点数N=500，码速率ps=16 MHz，模拟不同的载波频率(为210～260 MHz，间隔0.1 MHz)，加入10 dB信噪比高斯白噪声,连续501次测频，未加噪声与加噪声的测频误差如图8所示。

图7 未加入噪声测频误差变化图和加入噪声后测频误差变化图

图8 未加入噪声测频误差变化图和加入噪声后测频误差变化图

由图8可知,未加入噪声时最大测频误差不超过21 kHz，均方误差为12.9 kHz;加入噪声后最大测频误差不超过55 kHz，均方误差为25.9 kHz。测频误差大大降低。

以采样率为fs=1 000 MHz，采样点数N=500，码速率ps=16 MHz，模拟相同载波频率(为210 MHz)，加入10 dB信噪比高斯白噪声，连续501次测频，未加噪声与加噪声的测频误差如图9所示。

由图9可知,未加入噪声时最大测频误差不超过36 kHz，均方误差为11.1 kHz；加入噪声后最大测频误差不超过70 kHz，均方误差为11.0 kHz。 测频误差大大降低。

不同仿真测试结果如表1所示。

由仿真结果可知，未加噪声的测频误差小于加入噪声的测频误差。在加入噪声的情况下，最大测频误差不超过70 kHz，最大均方误差不超过30 kHz。在采样点数较少、又不能增加采样点数的情况下，频率估计精度提高，使得IFF模式5可以在短时间内提高信号的测频精度。

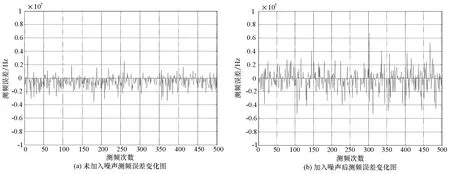
图9 未加入噪声测频误差变化图和加入噪声后测频误差变化图

表1 IFF模式5 MSK信号测频精度测试结果

4 结束语

本文所论述方法简单有效，不需要对原信号加窗，运算量小，易实现快速精确测频。这对于提高IFF模式5的MSK信号测频精度是有益的。经过试验仿真证明，该方法可用于IFF模式5，能够提高作战的准确性，具有一定的实际意义与应用价值。

[1] 邱宏坤，杨建波，毛虎.MARK XIIA Mode5系统仿真及抗干扰性能分析[J].火力与指挥控制,2011,36(2):104-106.

[2] 祝远平.中频数字接收机MSK信号调制解调及频率估计技术研究[D].成都:电子科技大学，2010.

[3] 谢春胜.一种高精度测频方法[J].电子信息对抗技术, 2008(23):18-21.

[4] 谢然.基于循环谱的通信信号参数估计算法研究与实现[D].郑州：解放军信息工程大学，2011.

[5] LYONS R G.数字信号处理[M].北京：机械工业出版社,2006.

ResearchintoHighAccuracyFrequencyMeasurementMethodofIFFMode5

ZHAN Yin-fang,WANG Jiang-bo

(The 36th Research Institute of CETC,Jiaxing 314033,China)

This paper studies the method to improve the accuracy of frequency measurement based on identification of friend or foe (IFF) mode 5 interrogation signal in the conditions of the number of sampling points is small and the number of points can't be increased,uses fast Fourier transform (FFT) frequency measurement to evaluate the signal carrier wave frequency roughly,utilizes spectrum peak position interpolation correction mode to reduce the frequency estimation error and increase the accuracy of frequency measurement in the case of nosie-free and adding Gaussian white noise.Simulation results show that the method is simple and can effectively improve the accuracy of frequency measurement.

identification friend or foe;frequency measurement;fast Fourier transform;accuracy

TN971.1

A

CN32-1413(2017)05-0012-06

10.16426/j.cnki.jcdzdk.2017.05.003

2017-05-08