一种时差定位系统模糊分析
2017-11-20齐永梅刘铸华陈凯翔
齐永梅,刘铸华,陈凯翔
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
一种时差定位系统模糊分析
齐永梅,刘铸华,陈凯翔
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
针对四站时差定位系统求解非线性方程组出现的模糊问题,从定位效能、布站优化、先验信息提取方面进行综合考虑,分析了消除模糊值的3种方式,并通过工程项目的仿真分析,得到一种时差定位系统的最优配置方式。
时差定位;模糊;效能;布站;先验信息
0 引 言
四站时差定位系统具有定位精度高、战场隐蔽能力强等优点,对于现役装备抗打击、灵活布放等要求具有较高的适应能力。四站时差定位系统采用三维空间内的4个观察站数据,进行时差参数提取,进而反推目标位置。
一般情况下,三维定位需要4个观测站同时接收辐射源信号,得到3组互不相关的时差,从而规定目标所在的3个双曲面,其交点就是目标位置。但是由于定位方程组的非线性,因此解算过程会出现多解的情况,即模糊产生。
针对一种空间四站时差定位系统的模糊产生原理进行分析,本文从模糊区对定位效能的限制、布站对消模糊的优化、先验信息对消模糊的影响进行仿真分析,给出了一种时差定位系统的最优配置方式。
1 四站时差定位原理
在三维空间中,辐射源信号到达2个观测站的时间差可以确定以2个观测站为焦点的双曲面。4个观察站规定的双曲面即为辐射源位置。
设空间时差定位系统由1个主站O(x0,y0,z0)和3个副站A(x1,y1,z1)、B(x2,y2,z2)和C(x3,y3,z3)构成,辐射源为X(x,y,z),如图1所示。通过比较信号到达4个站的时间,即可测量得到3个时差:

图1 四站时差定位示意图
(1)
定义距离:

i=0,1,2,3
(2)
因此上述时差测量实质为距离差:
(3)
式中:c为电磁波的传播速度。
将距离公式(2)代入式(3)进行移项并平方后,整理可得:
(x0-xi)x+(y0-yi)y+(z0-zi)z=
ki+r0·Δri,i=1,2,3
(4)

为求解式(4)所确定的非线性方程组,可先将r0看做一个已知量,从而得到如下表达式:
AX=F
(5)

当3个副站在x、y、z这3个方向均不等值时,A可逆,并且有:
(6)
令A-1=[aij]x×3,由式(6)可计算得到辐射源坐标:
(7)
其中:
(8)
将式(7)代入式(2)中r0的表达式,得到:
(9)
(10)
通过式(9)求解r0,即可得到辐射源位置[1]。
2 模糊区对定位效能影响分析

由于基线长度决定了时差测量精度,进而影响定位精度,根据实际应用要求,主站与副站之间基线长度控制在5 km~10 km。受空间观察站的灵敏度和视角范围影响,为保证一定的地面探测区域,需要将观察站控制在200 km~100 km以内。选取三角形布站进行分析,站间距离及高度如图2所示。

图2 三角布站示意图
选取主站O(0,0,0)和3个副站A(-5,5,0.1)、B(0,5,-0.2)和C(5,5,-0.1)。辐射源X(x,y,z)中的z表示相对高度,由200 km下降到100 km。因此模糊区如图3所示。

图3 三角布站模糊区随基线、高度变化示意图
三角形布站时,选择5 km固定基线,高度从200 km到达100 km过程中,模糊区变化如图4所示。

图4 固定5 km基线模糊区随高度变化示意图
可见在5 km的固定基线长度下,主副站高度被限定在130 km以上,才能保证对地面半径为120 km的圆范围内无模糊探测。
在200 km的固定主副站高度下,基线长度由5 km进行拉伸,模糊区随基线长度变化情况如图5所示。

图5 固定200 km高度模糊区随基线变化示意图
可见在200 km的高度下,要保证6.3 km以内的基线长度才能保证无模糊探测。
在选择三角形布站形式下,主副站基线5 km条件下,要保证半径120 km的探测范围,需保证130 km以上高度;保证同等探测范围,且保持200 km以上的高度,主副站基线可以拓展到6.3 km。综合考虑探测距离与抛投高度的限制,调整基线长度和探测高度来消除模糊区意义不大。
3 布站对模糊区影响分析
考虑到上一节的结论,从布站优化角度来消除模糊区。
选择星状布站时,站间距离及高度如图6所示。
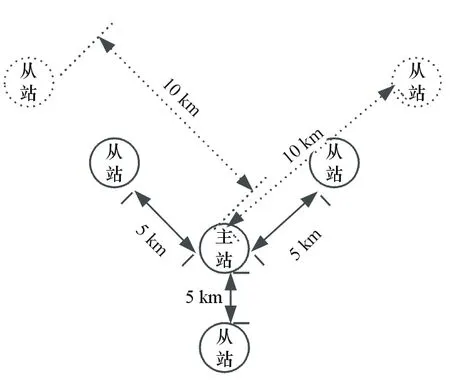
图6 星状布站示意图
选取主站O(0,0,0)和3个副站A(-5×cos30°,2.5,0.1)、B(5×cos30°,2.5,-0.2)和C(0,-5,-0.1)。辐射源X(x,y,z)中的z表示相对高度,由200 km下降到100 km。模糊区变化如图7所示。

图7 星状布站模糊区示意图
采用菱形布站时,布站形式如图8所示。
选取主站O(0,0,0)和3个副站A(5×cos30°,2.5,0.2)、B(5×cos30°,-2.5,-0.2)和C(10×cos30°,0,-0.2)。辐射源X(x,y,z)中的z表示相对高度,由200 km下降到100 km。模糊区变化如图9所示。
为保证时差定位精度及站间通信可靠性,主副站之间基线长度限定为5 km~10 km;为保证地面探视区域范围,受波束宽度限定,主副站高度范围限定为200 km~100 km。因此,从布站方式上选择星状布站可以从根源上消除模糊区的产生[2]。

图8 菱形布站示意图
4 利用先验信息消除模糊
采用星状布站时,根据公式(3),在进行主副站之间的时差测量时r1-r0=Δr1=c×Δt1,如果Δt1内仅存在单脉冲,则r0解唯一。当Δt1内出现多个脉冲时,如果多站间的脉冲不匹配,则会出现以下的模糊解[3]:
(11)


图9 菱形布站模糊区示意图
为方便分析,假定各观测站与辐射源之间的距离内具有等量的脉冲。由公式(11)可知,脉冲匹配错误,会根据脉冲数N具有N4种时差测量匹配结果,其中4为观察站的个数。模糊值的个数为:
n=N4-N
(12)
选择星状布站,主站为O(0,0,0)和3个副站A(-5×cos30°,2.5,0.1)、B(5×cos30°,2.5,-0.2)和C(0,-5,-0.1),当N=3时,投影结果和空间定位结果如图10所示。

图10 星状布站脉冲匹配模糊示意图

由于具有GPS定位等辅助手段,因此可以将目标定位值限定在以真实位置为圆心、60 km为半径的圆内。由目标分布规律,可以将目标定位值限定在地理表面10 km高度范围内。利用该先验信息,可以将目标的定位模糊值进行剔除,剔除结果如图11所示。
经过先验信息的剔除,可以得到较真实的轨迹。但是,由于虚假值的剔除,样本数量将会减少,在面对相控阵体制等具有低截获能力的雷达时,定位结果可信度将大大降低。为此,主从站截获脉冲均应传至主站进行脉冲匹配处理,从匹配全集中得到真值子集,提升样本可信度和完备度。

图11 星状布站消除脉冲匹配模糊示意图
5 结束语
本文对一种四站时差定位系统消模糊问题进行了研究,探讨了模糊区产生原理,从模糊区对定位效能影响、布站对消模糊的优化、先验信息对消模糊的改善进行了仿真分析。参照工程应用实际,给出了一种星状布站、近地目标定位的四站时差定位方案,具有较好的定位效果。
[1] 王永波,张令坤.多站时差定位技术研究[J].现代雷达,2003,25(2):1-4.
[2] 俞志强,叶朝谋.四站三维时差定位模糊分析[J].空军预警学院学报,2009,23(5):370-372.
[3] 任文娟,胡东辉,丁赤飚.一种新的利用时差相关性的时差分选配对方法[J].西安电子科技大学学报(自然科学版),2012,28(6):89-96.
AmbiguityAnalysisofATDOAPositioningSystem
QI Yong-mei,LIU Zhu-hua,CHEN Kai-xiang
(The 723 Institute of CSIC,Yangzhou 225001,China)
Aiming at the problem that ambiguity may occur while using 4-station time difference of arrival (TDOA) positioning system to resolve non-linear equations,this paper synthetically considers the positioning efficiency,station distribution optimization,extraction of transcendental information,analyzes three ways to eliminate ambiguity,and fetches an optimal configuration mode of TDOA positioning system through simulating and analyzing the engineering project.
time difference of arrival positioning;ambiguity;efficiency;station distribution;transcendental information
TN971.1
A
CN32-1413(2017)05-0006-06
10.16426/j.cnki.jcdzdk.2017.05.002
2017-05-19
