雷达运动目标模拟平台解算方法

周红峰，张友益

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

雷达运动目标模拟平台解算方法

周红峰，张友益

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

介绍了一种雷达运动目标模拟平台，基于D-H方法建立了这种平台的运动模型，用不同方法对平台进行了正运动学及逆运动学分析，采用对比法对分析结果进行验证，通过仿真验证了建立的运动学模型的准确性。

摇臂；雷达模拟；运动目标;解算方法

0 引 言

随着雷达技术的发展和雷达仿真试验要求的不断提高，需要在暗室内场条件下或者外场条件下实现雷达运动目标的模拟。根据这样的需求，为了实现从雷达角度看到俯仰及方位的运动目标，通常采用移动的信号源方法。按照这样的模拟原理，可采用喇叭阵列、矩形扫描架、摇臂平台等几种实现方案来实现信号源运动。

喇叭阵列方案采用二维平面空间排布的喇叭阵列，通过不同喇叭之间的切换模拟目标的运动。由于喇叭与喇叭之间是离散排布，目标空间覆盖是离散的，导致模拟出来的目标轨迹也是离散的，存在较大的离散误差。

采用扫描框架方案，需要比较大的框架以及横竖移动机构。内场应用时，由于较小场景相对容易实现，外场应用时需要大跨度支撑框架以及横竖移动机构，实现复杂，灵活性差。

摇臂式目标运动模拟方案相对前2个方案能够实现连续的目标轨迹，布置灵活，安装相对简单，但控制相对复杂。

本文对摇臂式目标模拟方案原理及解算数学模型进行了理论分析和推导。具体的摇臂运动平台可以依据解算模型设计伺服控制系统软件，结合具体的平台参数实现目标的模拟。

1 摇臂平台目标模拟原理

图1 目标模拟原理图

摇臂模拟平台布置在雷达与将要模拟的目标之间。摇臂平台控制信号源三维运动，使信号源始终位于雷达与要模拟目标之间的连线上。模拟器的方位俯仰运动，通过图1的关系可以转换成模拟目标的方位俯仰运动。数学上，摇臂的运动轨迹为目标运动轨迹在摇臂运动曲面上的投影。具体投影方法为：雷达目标和雷达的连线与摇臂运动曲面相交，交点为投影点。

2 摇臂平台运动链与正运动学分析

要研究摇臂系统，首先要进行摇臂运动平台运动链及运动学分析研究。对摇臂平台运动学分析是对摇臂平台运动控制的基础。摇臂运动平台运动学问题包含正向解和逆向解问题。正向解问题是摇臂根据每个运动副设定关节变量值，得到信号源的空间位置和方向的解算过程。逆向解问题是根据信号源运动轨迹和方向的要求，解出各个运动副关节的变量(未知的关节参数)。本节先研究摇臂运动链及正向解问题，下节研究逆向解问题。

摇臂运动平台是典型的串联机械手结构，由简单的运动链所组成。如图2所示的摇臂运动平台由0到5号6个杆件组成。其组成的每个杆件最多只和2个其他杆件相连。端部的2只杆件只和1个杆件相连，第0号杆件为基座，第5号杆件是末端执行器(即信号源)。除了端部的杆件，其它的杆件都包含2个运动副，而且都是转动副(rotating pair)。1号到4号杆件为中间杆件，它们都为双运动副杆件，其两端转动副分别为R1～R5。

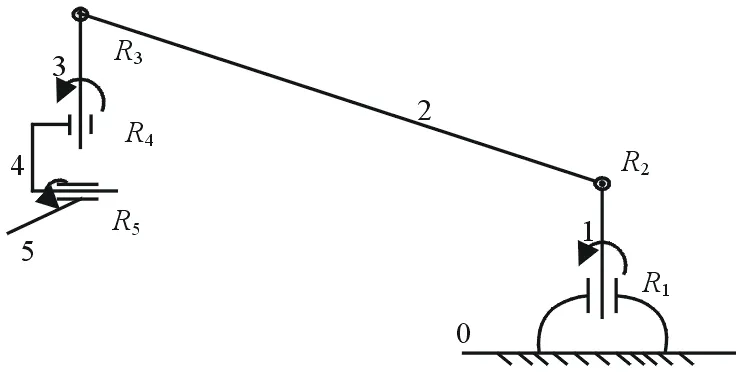
图2 摇臂运动模拟平台运动链杆件图

为了唯一描述运动链的结构，即确定相邻2个运动副之间的相对位置与方向，这里采用Denavit-Hartenberg提出的D-H方法[1]。

图2所示的摇臂平台结构由5个转动副构成。描述摇臂平台的状态，可以用这5个转动副的关节变量以及表征运动副之间位置关系的关节参数表示。

根据D-H方法，在图2中已经定义i=0,…,5号杆件，0号为基座，5号为执行器。以下为了叙述方便采用i=0,…,5计数多个连续的运动副、杆件、坐标系等。

定义0,…,5号运动副的轴Zi(i=0,…,5)。Xi同时与Zi-1和Zi垂直，方向为Zi-1到Zi，符合右手定则。Zi-1与Zi之间距离定义为ai，Xi+1与Zi的交点在Zi上的坐标为bi。Zi-1与Zi之间夹角定义为αi，Xi与Xi-1之间夹角定义为θi。对于摇臂运动链结构(摇臂结构的形位和姿态)，可以用每个运动副Ri的参数ai，bi，αi，θi等描述，表示为Ri(ai，bi，αi，θi)。根据上述定义，对于本文的摇臂平台，θi是未知量，是关节变量，而其他参数在设计具体摇臂时都已确定。

D-H方法可以描述摇臂平台，用以确定信号源在杆件坐标系的结构、形位或姿态。为了进一步对摇臂平台进行运动分析，需要定义相关信号源的笛卡尔坐标系关节坐标系，如图3所示。

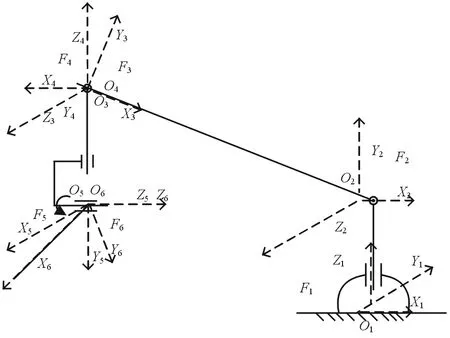
图3 摇臂运动平台D-H法分析

具体过程如下：定义Fi为以Oi为原点，(Xi，Yi，Zi)为轴的坐标系，Fi固定在i-1号杆件上。正向求解可以通过相关的坐标旋转、移动等实现。设Qi为坐标系Fi(Xi，Yi，Zi)旋转到坐标系Fi+1(Xi+1，Yi+1，Zi+1)的旋转矩阵。设Ai为Oi到Oi+1的矢量。矩阵Qi可以按照几何学定义，用ai，bi，αi，θi参数实现：

(1)

设Q为末端信号源的方向，A为末端执行器工作点的位置，则：

Q=Q1Q2Q3Q4Q5

(2)

A=A1+Q1A2+Q1Q2A3+Q1Q2Q3A4+

Q1Q2Q3Q4Q5A5

(3)

对于具体的摇臂平台，在设计时相邻轴间多采用垂直或平行关系，如Z2⊥Z1，Z3∥Z2，Z4⊥Z3，Z5⊥Z4，解耦相关运动关系，简化旋转矩阵复杂度，也方便最终的摇臂控制。

3 摇臂平台逆运动学分析

对于本文中逆向解问题是按照设定好的目标轨迹要求，通过逆运动解算，获得控制信号源的空间位置的每个运动副未知变量数值。在模拟过程中正向用这些数值控制运动副关节运动，复原出信号源空间位置，使信号源按要求正好位于雷达与模拟目标的连线上。

经前节分析每个关节运动副的参数除θi未知，其余都是已知量，所以摇臂运动平台逆向问题就是求解未知的变量θi。具体可以采用上节D-H法得出的公式和具体的约束条件列写相关方程进行求解。但这个逆解算过程需要通过消元后解非线性方程组得到解答，过程比较复杂，还会出现多重根的情况。

根据摇臂模拟平台的目标模拟原理，具体的约束条件是，平台输入是目标的空间坐标位置，只能够确定目标与雷达之间的连线，要求摇臂平台控制的信号源在这条连线上，并且辐射源要方向要对准雷达。

由上分析可知，摇臂承载负载信号源的位置没有直接给出，需根据约束要进行求解。根据摇臂平台的具体要求得到:

(4)

式中：T为目标的位置坐标；Tr为雷达的位置坐标；第1个方程表示信号源的指向于目标与雷达的连线平行；第2个方程表示A位于雷达与目标的连线上；第3个方程表示杆3与杆1平行，都垂直于基座，这是摇臂运动的附加约束条件。

将式(1)、(2)和(3)的关系带入式(4)，可以得到5元的非线性方程组，解这个方程组，能够得到摇臂每个关节转角角度θi的值。

上述方法求解比较复杂，对于简单的结构能够获得闭式的解，复杂的结构有可能需要通过数值方法给出解。针对文中的摇臂平台，本文给出了一种相对简单的几何解析法来求解摇臂平台逆运动问题。该方法充分利用摇臂平台设计特殊的空间结构，尽量多地进行运动解耦，简化摇臂平台的解算过程。

首先分析由这5个转动副构成的运动学链。摇臂平台模型如图4所示。

图4 摇臂运动平台结构及运动副转角定义

平台为5轴系统，通过运动副的特殊位置设置，满足摇臂平台运动模拟要求，同时对5轴系统运动关系进行简化。ψ1、β1构成一级向上叉架结构，垂直相交；ψ2、ψ3构成向下的叉架结构，垂直相交；β1、β2轴向平行，可认为是一个平面机构；β1、β2互补，保证ψ1、ψ2轴平行且与大地垂直。

对运动目标模拟的方法为控制ψ1、β1、β2、ψ2、ψ3，使信号源始终处于雷达天线与目标连线上，使信号源始终对准雷达。根据上述定义，建立相关坐标系如图5所示。

雷达位于坐标原点，雷达与摇臂基座连线为X轴方向，Z方向垂直向上，Y方向符合右手定则。

图5 摇臂运动平台几何解析法分析模型

设虚拟的圆心在O(a,b,c)，摇臂臂长R，摇臂垂直于XY平面，且垂点位于X上(为了简化)。S(x,y,z)为信号源位置,S′是S在XY平面的投影点。T(xt,yt,zt)为模拟的目标位置。

计算S(x,y,z)点：

(5)

a2+b2+c2-R2=0

(6)

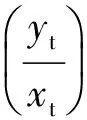
(7)

这里取较小的根，即：

(8)

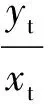
根据图5 模型可解出ψ1、ψ2、ψ3、β1、β2等角度。

4 模型验证

为了验证前述不同模型的正确性，采用2种模型相互验证的方法来实现。具体思路为：设置摇臂平台的基本参数、目标位置、雷达位置，根据这些输入参数代入逆运动几何解析法模型，得到摇臂平台的控制参数及信号源位置坐标。将摇臂的控制参数代入，用D-H法得出正向解算模型，得到信号源位置坐标，验证两模型信号源位置坐标是否相同，由此来验证2个模型的一致性。

设置摇臂参数，如图2中杆1长2 m，杆2长2 m，杆3长5 m；图3中Z3到Z5距离2 m，X1到X2距离2 m，Z2到Z3距离5 m，X4到X5距离2 m。

目标在以雷达为原点的坐标系中的位置为(20 000,500,2 000)，单位m。雷达到摇臂平台距离100 m。

逆运动几何解析法模型计算如下：

根据第3节中描述的模型以及摇臂输入参数，得出模型的输入参数：a=100 m,b=0 m,c=2 m,R=5 m,xt=20 000 m,yt=500 m,zt=2 000 m。计算得到：信号源位置为S(95.715 4，0.957 2，2.392 9)，ψ1=12.592 7°，ψ2=13.165 7°，ψ3=1.432 2°，β1=118.592 5°，β2=61.407 5°。

D-H法正运动模型计算：根据摇臂输入参数、第2节中相关定义和图3得到模型的输入参数α1=0°，α2=90°，α3=0°，α4=90°，α5=90°；A1到A5矢量为A1=(0,0,2)′，A2=(-5cosθ2, -5sinθ2,0)′，A3=(0, 0,0)′，A4=(0, 0,-2)′，A5=(0, 0,0)′。

根据图3和图5的模型，以及第1节描述的方法，依据逆运动模型计算结果，可得到：θ1=-12.592 7°,θ2=-28.592 5°,θ3=151.407 5°,θ4=13.165 7°,θ5=1.432 2°。各旋转副的关节参数为：

R1(a1=0 m,b1=2 m,α1=0°,θ1=-12.592 7°)；

R2(a2=0 m,b2=0 m,α2=90°,θ2=-28.592 5°)；

R3(a3=5 m,b3=0 m,α3=0°,θ3=151.407 5°)；

R4(a4=0 m,b4=-2 m,α4=90°,θ4=13.165 7°)；

R5(a5=0 m,b5=0 m,α5=90°,θ5=1.432 2°)。

根据公式(2)、(3) 得到：

A=(-4.284 6,0.957 2,2.392 9)′

A为信号源位置矢量，由于图3和图5之间坐标系原点X方向差100 m，换算到图5坐标系中：

(-4.284 6+100,0.957 2,2.392 9)=(95.715 4，0.957 2，2.392 9)

结果与S相等，验证了这2种模型的正确性。

5 结束语

摇臂式运动平台的运动学分析是摇臂平台设计的基础，也是目标模拟的基本模型。本文给了摇臂式雷达目标模拟平台的模拟原理，分析了摇臂式运动平台的运动链并进行了运动学分析，给出了相关仿真验证。在摇臂平台具体技术设计过程中必须进行动力学分析，即研究摇臂平台在运动过程中速度、加速度等问题。动力学问题可以以运动学研究为基础，利用运动学研究的结果和相关公式。另外摇臂平台的伺服控制也是建立在摇臂运动学和动力学分析的基础上。本文的研究为摇臂雷达目标模拟器的控制研究提供了基础的运动学解算模型和方法，更深入的研究还需要进一步开展。

[1] 宋伟刚.机器人学[M].北京：科学出版社，2007.

[2] 数学手册编写组.数学手册[M].北京：人民教育出版社，1979.

SolvingMethodofSimulationPlatformofRadarMovingTarget

ZHOU Hong-feng,ZHANG You-yi

(The 723 Institute of CSIC,Yangzhou 225001,China)

This paper introduces a simulation platform of radar moving target,builds the moving model of the platform based on D-H method,performs the analysis of forward kinematics and inverse kinematics to the platform through different methods,adopts comparison method to validate the analyzing result,validates the veracity to build moving dynamatic model through simulation.

rocker arm;radar simulation;moving target;solving method

TN955.2

A

CN32-1413(2017)05-0040-04

10.16426/j.cnki.jcdzdk.2017.05.008

2017-09-10