如何培养初中生利用二次函数解决问题的能力
2017-11-17江苏省丰县创新外国语中学唐义琴
江苏省丰县创新外国语中学 唐义琴
如何培养初中生利用二次函数解决问题的能力
江苏省丰县创新外国语中学 唐义琴
二次函数属于初中数学内容的一部分,它与代数、三角函数等相联系。近几年,由于二次函数题目灵活,难度较大,因此在综合题型中所占比例较大。基于此,本文对如何培养初中生利用二次函数解决问题的能力进行研究,采用文献法、实例论证法等,从利用几何画板视角,提出培养初中生利用二次函数解决问题能力的方法,为数学教育工作者教授二次函数提供一定的帮助,对推进素质教育具有重要的现实意义。
初中生;二次函数;解决问题;能力
目前,由于受传统教学方法的影响,初中生对数学知识的利用能力不强,特别是利用二次函数解决问题的能力较弱,这不仅是由于二次函数所涉及的内容较多,还与学生自身的学习能力有关。为了培养初中生利用二次函数解决问题的能力,本文从自主探究方法、数形结合法及化归转换法使用去解决相关问题,以此提高初中生利用二次函数解决问题的能力。
一、利用自主探究方法解决函数图形变化中说理问题
在数学学习中,学生是学习的主人,通过老师的引导参与到学习活动中去,从而获得各种知识。而自主研究类题目是先对给定的一个图形进行研究,然后在某些条件发生改变时,则相应给定的图形会发生改变,相关的理论也会发生改变。
例如:在如下的直角坐标系中,点A是二次函数y=x2在第二象限内的任意一点,连接OA,过点O作OB⊥OA,与图象相交于点B,分别以OB、OA为边构造矩形ACBO。如图1所示,当点A的横坐标为 时,矩形ACBO是一个正方形。

图1
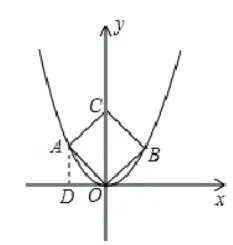
图2
分析:过点A作x轴的垂线,垂足为点D,因为四边形AOBC为正方形,所以∠COA为45°,那么,∠AOD=45°。通过证明得到△AOD是等腰直角三角形,将A点的坐标设为 (-a,a),把点A坐标代入y=x2计算即可。
解:(1)如图2,过点A作AD垂直x轴于点D,
∵矩形AOBC是正方形, ∴∠AOC=45°,
∴∠AOD=45°,
∴△AOD是等腰直角三角形,
设点A(-a,a)(a≠0),
∴(-a)2=a,
∴a1=-1,a2=0(不合题意,舍去),
∴-a1=-1,
∴当点A的横坐标为 -1 时,矩形ACBO是一个正方形。
二、利用数形结合法解决函数图形变化中蕴含的函数问题
函数图形变化的试题比较难,通常在考试压轴题中出现。图象运动变化作为主要特征,在变化的过程中,需要找到两个变量之间的某种关系,根据题目的要求,以此求解自变量的取值范围,最终寻找出符合题目条件的特殊性,这种特殊性需要应用数形结合思想。
例如:如图3,已知直线l:y=-x+2与y轴相交于点A,二次函数y=(x-1)2+k经过点A,顶点为点B,另一个函数y=(x-h)2+ 2-h(h>1)的顶点为点D,两个二次函数的图象相交于点C。(1)求出点B的坐标,并说明点D在直线l上;(2)设交点C的横坐标为m,则交点C的纵坐标为多少?由此进一步探究m关于h的函数关系式。

图3

图4
分析:对于此题,若想求m的大小,需要将以上的数值进行求解,具体步骤如下:
解:(1)当x=0 时,y=2, ∴A(0,2),
∴1+k=2 ,∴k=1, ∴B(1,1)。
∵D(h,2﹣h),
∴当x=h时,y=﹣x+2=﹣h+2=2﹣h。
∴点D在直线l上。
(2)∵点C为两二次函数图象交点,

三、利用化归转换法解决函数图象中动点形成的相似问题
二次函数是初中函数的主要内容,作为高中圆锥曲线的基础,通常与相关的几何图形相联系,其涉及最大面积、最小距离的问题,需要建立二次函数关系式,通过运用二次函数解决实际问题。对于函数图象中动点形成的相似问题,需要根据图形之间的数量关系,利用数形结合思想与方程思想,形成一元二次方程,求解点的坐标,得到函数解析式。利用几何画板,反映其几何关系,当条件和结论变化时,从诸多方面对数学问题的变化进行分析,在不同条件下找到解决问题的方法,将代数问题转化为几何问题,把抽象问题转化为形象问题,以此促进学生积极思考。
例如:如图5,二次函数y=ax2+bx+c的图象与x轴的交点A的坐标为(1,0),交点B的坐标为 (2,0),与y轴相交于点C(0,2),过点A、点C画直线AC。(1)求二次函数的解析式; (2)若点P在x轴的正半轴上,并且PA=PC,求线段OP的长度。

图5
分析:(1)已知图象与x轴的两个交点A、B的坐标,设交点式解析式,先将点C(0,2 )代入,求二次项系数a的值也就不难了,从而得到抛物线解析式。(2)假设OP=x,那么PC=PA=x+1,在直角三角形COP中,依据勾股定理列一元二次方程,解方程得出OP的长度。
解:(1)根据题意,设 y=a(x+1)(x-2)( a≠0),
∵C(0,-2),∴﹣2=a(0+1)(0-2),
∴a=1, ∴ y=(x+1)(x﹣2),
即 y=x2-x-2。
(2)假设OP=x,那么PC=PA=x+1,
在 Rt△ POC 中,x2+22=(x+1)2,
∴ x=OP=1.5。
综上所述,要培养初中生利用二次函数解决问题的能力,可以从自主探究方法、数形结合法及化归转换法的使用进行展开,通过具体实例进行分析,有利于学生利用二次函数解决相关问题,为数学教育工作者教授二次函数提供一定的帮助,对推进素质教育具有重要的现实意义。
[1]唐娟.初中生二次函数学习困难的原因分析及对策[D].海南师范大学,2015.
[2]尹玉珍.利用几何画板提高初中生二次函数解题能力的方法研究[D].宁波大学,2014.
[3]张晓娟.二次函数的教学策略[J].语数外学习(初中版中旬),2014(04):37.…
[4]高永慧.初中生理解二次函数实际问题困难的原因及对策[D].山东师范大学,2013.
[5]赵立国.浅谈二次函数的重要作用[J].考试(教研),2011(03):62.…
