一种回归模型异方差性的检验方法*

2017-11-16朱元正

重庆工商大学学报（自然科学版） 2017年6期

关键词：数据量样本量方差

朱元正

(重庆工商大学数学与统计学院，重庆 400067)

一种回归模型异方差性的检验方法*

朱元正

(重庆工商大学数学与统计学院，重庆 400067)

针对现有回归模型异方差性检验的局限性，借鉴尺度参数检验与重抽样方法的思想，通过对残差序列进行随机抽样，提出了一种可行的非参数检验方法；该方法具有更强的适用性，Monte Carlo模拟结果表明，其检验效果良好，尤其针对样本量较小的情形。

回归模型;异方差性;随机抽样;假设检验

0 前言

经典回归分析中，随机干扰项的方差齐性作为一项基本假定，保证了通常的t检验、F检验、以及模型预测等统计推断得以顺利实施。在该前提条件不成立时，若仍直接采用一般方法估计模型，将无法取得理想的拟合效果，也会获得一些虚假结论。因而异方差性的检验方法成为回归分析中一项重要课题。

观察残差图是异方差检验最为简单直观的方法，也可以通过残差分析[1]来构造相关检验；Goldfeld S和Quandt R[2]针对单调情况的异方差提出了分组样本的F检验；Park R，Glejser H认为异方差的产生与某一解释变量有关[3]，并分别提出了各自的检验方法；Halbert White[4]利用LM检验思想得到经典的White检验方法；随后Cook与Weisberg提出另一种LM检验[5]，Davidian 与Carroll、Carroll与Ruppert分别得到异方差的伪似然检验[6]。这些方法均基于随机干扰项的正态假定来研究，而Bickel[7]则把检验框架拓展到非正态的情况。此外，还有诸如Spearman相关系数法，非参数蒙特卡罗(NMCT)等检验方法[6]。

上述检验方法尽管有所不同，但存在一个共同思路：随机干扰项的异方差性与解释变量有关。在模型设定不存在偏误的情况下，这种检验思想具有一定合理性，既能判断异方差存在与否，又能确定其来源。然而，由于现实数据的多样性与复杂性，往往会受到解释变量之外诸多因素的综合影响。就截面数据而言，不同样本点间通常存在空间“异质性”，对于时间序列数据，往往具有自相关性；同时，大部分检验方法通过“辅助回归”得以具体实施，此时的辅助回归模型中，其随机干扰项本身就可能不满足基本假定[3]。综上，传统的异方差性检验方法仍具有较强的局限性。

鉴于此，本文将在非参数框架下，借鉴多样本尺度参数与重抽样的检验思想，通过对残差序列随机抽样得到的分组数据，检验异方差存在性。该方法相比传统检验拥有更强的适用性，同时具有良好的检验效果。

1 理论基础

总体回归模型的一般形式是：

yi=fXi,β+εi，i=1,2,…,n

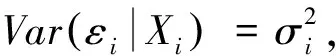
经典非参数统计方法对总体假定相对较少，以“秩”作为基础，研究“秩”及其统计量的分布，具有更好的稳健性，适用范围更广。其中，关于多样本尺度参数，即分布离散程度的检验有一些常见方法[8]，它们对混合样本进行排序，通过衡量各总体在混合序列中分散程度的差异来判断方差是否一致。不同方法间的区别在于对混合样本重新定义了不同的“秩”，各自设定的检验统计量也随之不同。其中，平方秩检验是最常用的方法，且与异方差检验问题特点相符，因此本文选择该方法进行探讨。

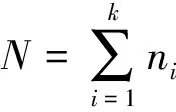
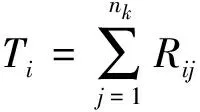
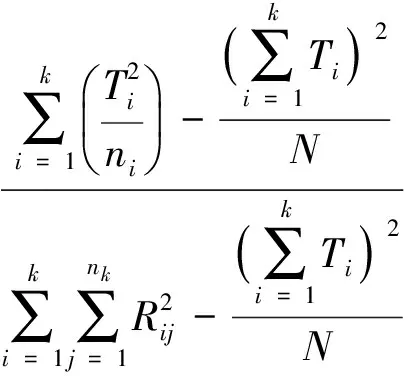
T用来衡量各Ti间的差异大小。在原假设下，检验统计量T渐进服从χ2k-1，可通过计算或查表得到p值，从而进行判断。

2 异方差性的检验方法

回归模型异方差性的检验问题为

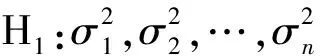
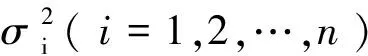
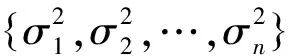
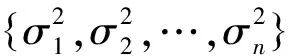
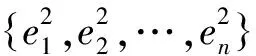
(3) 对这k组数据进行平方秩检验，若拒绝原假设，则停止，否则转至(2)，直至重复m次后结束。

3 Monte Carlo模拟

通过Monte Carlo方法产生理论参考数据验证上述异方差性检验方法的效果，试验重复次数T=10 000。

设定多元线性回归模型：

yi=β0+β1x1i+β2x2i+εi

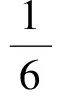
为了方便操作，设定各组样本量相同，即n1=n2=…=nk=l，选择不同的分组数k、各组样本量l进行试验，探究这些参数对检验效果的影响，运用R 3.3.0软件编程计算，部分检验结果如表1所示。

通过表1可知，无论参数如何设置，10 000次试验中均有85%以上能够检验出存在的异方差性，检验整体效果良好。由于抽样的随机性，在参数k，l相同时，检验结果也会存在较小差异；当k，l不相同时，分组数k对检验影响较小，每组样本量l越大检验效果往往越好。数据量的增大不会影响检验结果，甚至会提高效果，其原因在于数据量越大，关于随机干扰序列的信息越多，异方差性的表现就越明显。

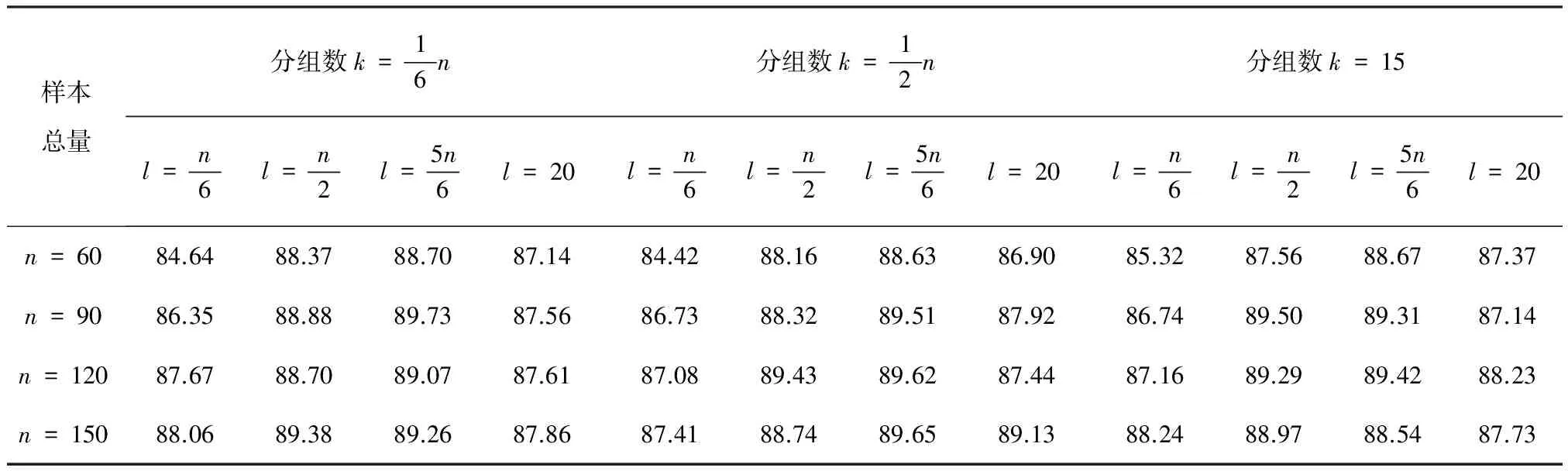
表1 不同参数下异方差性检验效果

由表1知，当k=15，l=20时，检验效果已经能够达到较高水平，此时计算量也适当，故在使用该方法时可以选择固定参数，即k=15，l=20。为进一步验证本文方法的有效性，在相同条件下采用White检验、B-P检验对模拟数据的异方差性进行探索，运用R 3.3.0软件编程计算，检验结果如表2所示。

表2 其他检验方法效果

结果表明：在样本量较少时，本文的异方差性检验方法具有更好的检验效果，这与重抽样方法的相关结论一致，也印证了该检验思想的合理性与科学性。但随着样本量的增加时，White检验等方法的效果会有明显的提高，当样本量充分多时，能够非常有效地检验出异方差。相对而言，本文的方法受数据量的影响较小，检验效果更稳定，在数据量很大时，其效果可能略逊于其他方法。

4 结论

针对传统异方差性假设检验方法的局限性，提出了一种新的非参数检验方法，适用性更强，其检验效果良好，尤其针对样本量较小的情形，但该方法计算量较大，需要借助计算工具才能实现。值得提出的是，当对实际数据有一定认识时，主观经验也可以用来产生特定的分组数据，以减少由随机分组带来的重复次数，计算效率可能更高。同时，通过计算发现，本文方法犯第一类错误的概率高于White检验等方法。因此，在具体使用时，应该先通过观察残差图等方法，在初步判定回归模型可能存在异方差性后，再通过该方法进一步推断。

[1] CARROLL R，RUPPERT D．Transformation and Weighting in Regression[M]．New York：Chapman and Hall， 1988

[2] GOLDFELD S，QUANDT R．Some Tests for Heteroskedasticity[J]．Journal of the American Statistical Association，1965(60):539-547

[3] 李子奈，潘文卿．计量经济学[M]. 3版．北京：高等教育出版社，2010

LI Z N，PAN W Q．Econometrics[M]．3rd edn. Beijing：Higher Education Press，2010

[4] WHITE H. A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity[J]．Econometrica，1980(48): 817-838

[5] 韦博成，林金官，吕庆哲．回归模型中异方差或变离差检验问题综述[J]．应用概率统计，2003 (10):210-220

WEI B C，LIN J G，LU Q Z．Developments of the Tests for Heteroskedasticity or Varying Dispersion in Regression Models[J]．Chinese Journal of Applied Probability and Statistics，2003(10):210-220

[6] 朱力行，许王莉．非参数蒙特卡罗检验及其应用 [M]．北京：科学出版社，2008

ZHU L X，XU W L．Non-parametric Monte Carlo Tests and Its Applications [M]．Beijing：Science Press，2008

[7] BICKEL P．Using Residuals Robustly I: Tests for Heteroscedasticity，Nonlinearity[J]．Annals of Statistics，1978(6):266-291

[8] 吴喜之．非参数统计[M]．2版. 北京：中国人民大学出版社，2006

WU X Z．Non-parametric Statistics[M]． 2nd edn. Beijing：China Renmin University Press，2006

[9] GIVENS，HOETINg J．Computational Statistics[M]．New York：Wiley， 2005

A Test for Heteroskedasticity in Regression Model

ZHUYuan-zheng

(School of Mathematics and Statistics，Chongqing Technology and Business University，Chongqing 400067，China)

In view of the deficiencies of heteroskedasticity tests existing in regression model，by using the ideas of multi-sample scale parameter test and resampling method，through sampling the residual sequence randomly，a feasible non-parametric test method is proposed．The method has a stronger applicability，and Monte Carlo simulation shows that it has a good test power，especially in cases of small sample size．

regression model; heteroskedasticity; stochastic sampling; hypothesis test

O212.1