绩效评价中分值聚合的多目标优化方法*

2017-11-16李茜婷陈培章赵克全

重庆工商大学学报（自然科学版） 2017年6期

关键词：对模型分值遗传算法

李茜婷，陈培章，赵克全

(重庆师范大学数学科学学院,重庆 401331)

绩效评价中分值聚合的多目标优化方法*

李茜婷，陈培章，赵克全

(重庆师范大学数学科学学院,重庆 401331)

评价分数的优化处理在绩效评价中具有重要意义，绩效评价中的分值处理过程包括评价分数的归一化处理和分数的聚合两个阶段；针对绩效评价中评价分数的聚合问题，建立了新的多目标优化模型，并利用遗传算法对模型进行了求解，其研究结果克服了最近由Andrés等人提出的360度绩效模型存在的一些不足。

绩效评价；分值处理；多目标优化；遗传算法

0 引言

众所周知，绩效评价在企业员工综合业绩考核，高校教师或行政管理人员工作质量考核，银行员工综合业绩考核，生态环境考核等诸多方面均有十分广泛的应用。绩效评价的发展历史悠久，从发展历史看，非正式的绩效评价有着极其悠久的历史，1980年Devris等人在文献[1]中指出，据历史考证中国人至少在公元3世纪已经应用正式的绩效评价。1987年Raymond在文献[2]中指出，1813年美国军方开始采用绩效评价，1842年美国联邦政府则将绩效评价应用于对政府公务员的考核。在此基础上，关于绩效评价的研究受到了大量学者的关注[3-5]。

最近，Andrés等人在文献[6]中提出了360度绩效评价方法，通过建立优化模型重点研究了评价分数的最优聚合问题。360度评价法也称全视角考核或多个考评者考核，它是一种全方位考核方法，由被评价者的上级、下级、同事、客户以及本人担任考评者，从多个角度对被评价者进行全方位的考核。360度评价法被广泛应用于企、事业单位对员工综合业绩的评价，它在人力资源部门考核员工绩效时有着重要的地位[7-9]。

值得注意的是，Andrés 等人[6]提出的360度绩效模型存在一些不足，例如，线性加权法权重向量的确定主观性太强；极小极大规划模型的多目标优化模型一般情况下是非光滑的，求解可能比较困难。受文献[6, 10]研究工作的启发，本文将针对绩效评价中评价分数的聚合问题，建立新的多目标优化模型，并利用遗传算法对模型进行求解。

1 问题提出

最优化模型与方法目前已被用于研究评价分数的处理问题，见文献[11-17]。特别地，Andrés等人在文献[6]中基于距离函数法，在传统360度评价模型的基础上提出了新的绩效评价方法，即360度绩效模型，并进行了数值实验。该方法将分值处理过程分为3个阶段，即归一化阶段、聚合阶段、评分阶段。针对分值的聚合问题建立了如下模型：

模型I

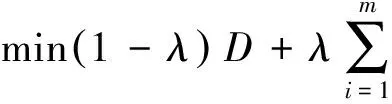
其中λ∈0,1，ηi和ρi分别表示目标分值与个体评估值的负、正偏差的绝对值；y*表示目标分值；ωi表示第i个标准相对于各个评价者的重要性；λ是针对每个被评价者的权系数；m表示评价标准个数。值得注意是模型I等价于如下模型：

模型II

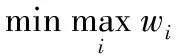
由于通常的极小极大规划模型一般是非光滑的，且其求解可能比较困难。因此，如何建立新的多目标优化模型以研究绩效评价中的分值聚合问题具有重要意义。

2 模型建立

本文在模型 I的基础上，建立如下修正的双目标优化模型以研究分值的最优聚合问题，并利用遗传算法对模型进行求解。具体的双目标优化模型如下：

模型III

minD

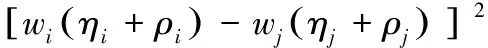
3 数值实验

为了对模型的数值实验效果进行比较，本文采用文献[6]中的数据。令X1和X2代表文献[6]中的两个被评价对象，Z1和Z2代表本文中的两个被评价对象。将评价分值进行归一化处理后的数据如表1所示。

将表1中的数据代入模型III中，并用遗传算法对模型进行求解，随机选取每层得到的有效分值代入下一层运算。随机选取的20组最终聚合分值见表2。Z1,Z2最终聚合分值的变化趋势如图1所示。

由表2和图1可知，Z1的聚合分值VZ1始终大于Z2的聚合分值VZ2，即VZ1>VZ2，很明显，利用本文所建立的双目标优化模型获得的聚合分值的变化较小，分布比较稳定且各聚合分值之间的差异较小。

为了与文献[6]中所采用的方法进行比较，将表1中的数据代入模型I中，并利用遗传算法进行求解，得到当λ取不同值时评价对象X1、X2的聚合分值见表3。X1、X2最终聚合分值的变化趋势如图2所示。

由表 3和图2可知，采用文献[6]中的方法而得到的最终聚合分值会随λ值的变动而改变，没有稳定的变化趋势且各聚合分值间的差异相对较大。

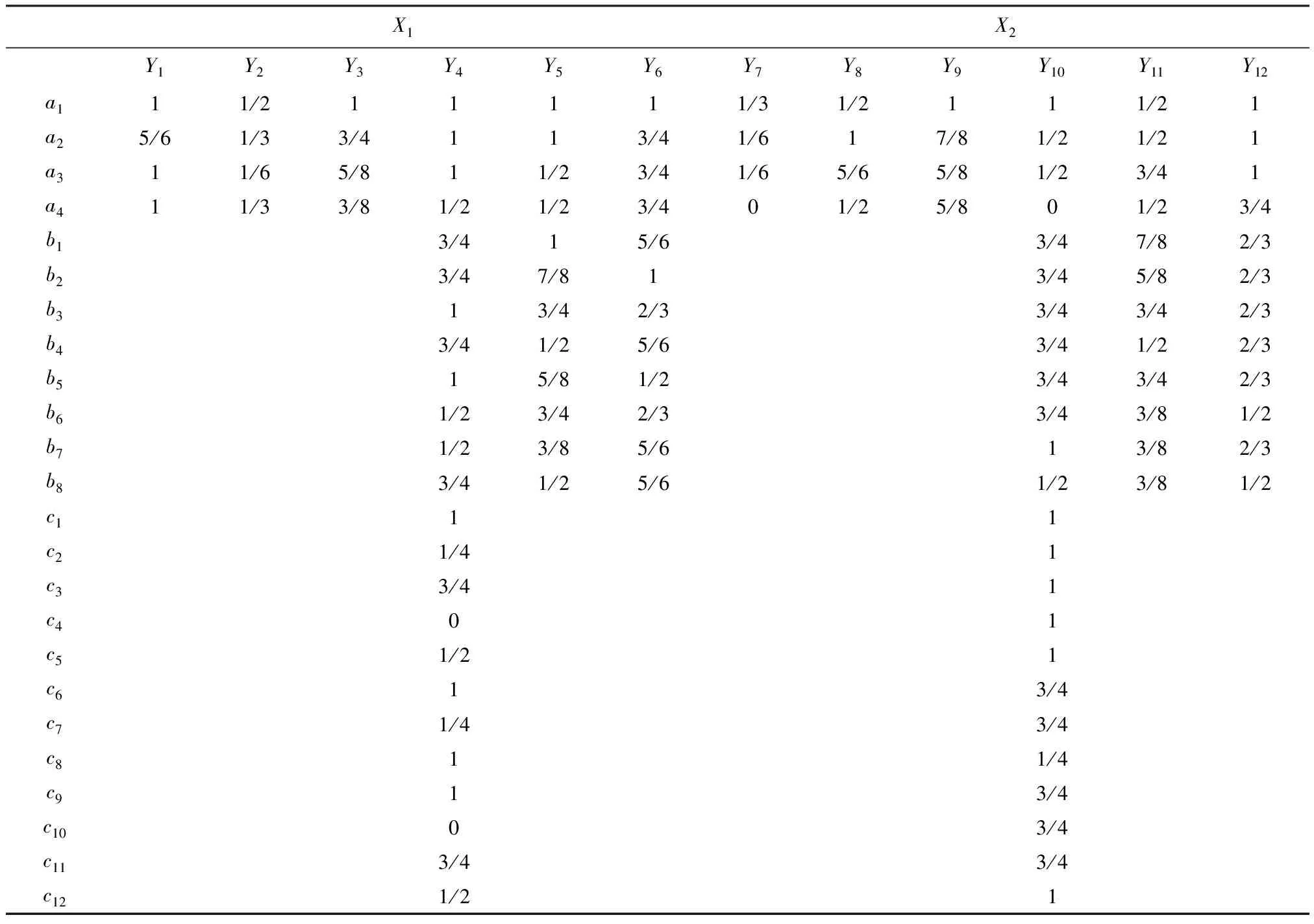
表1 归一化后的评价分值

表2 Z1、Z2的最终聚合分值

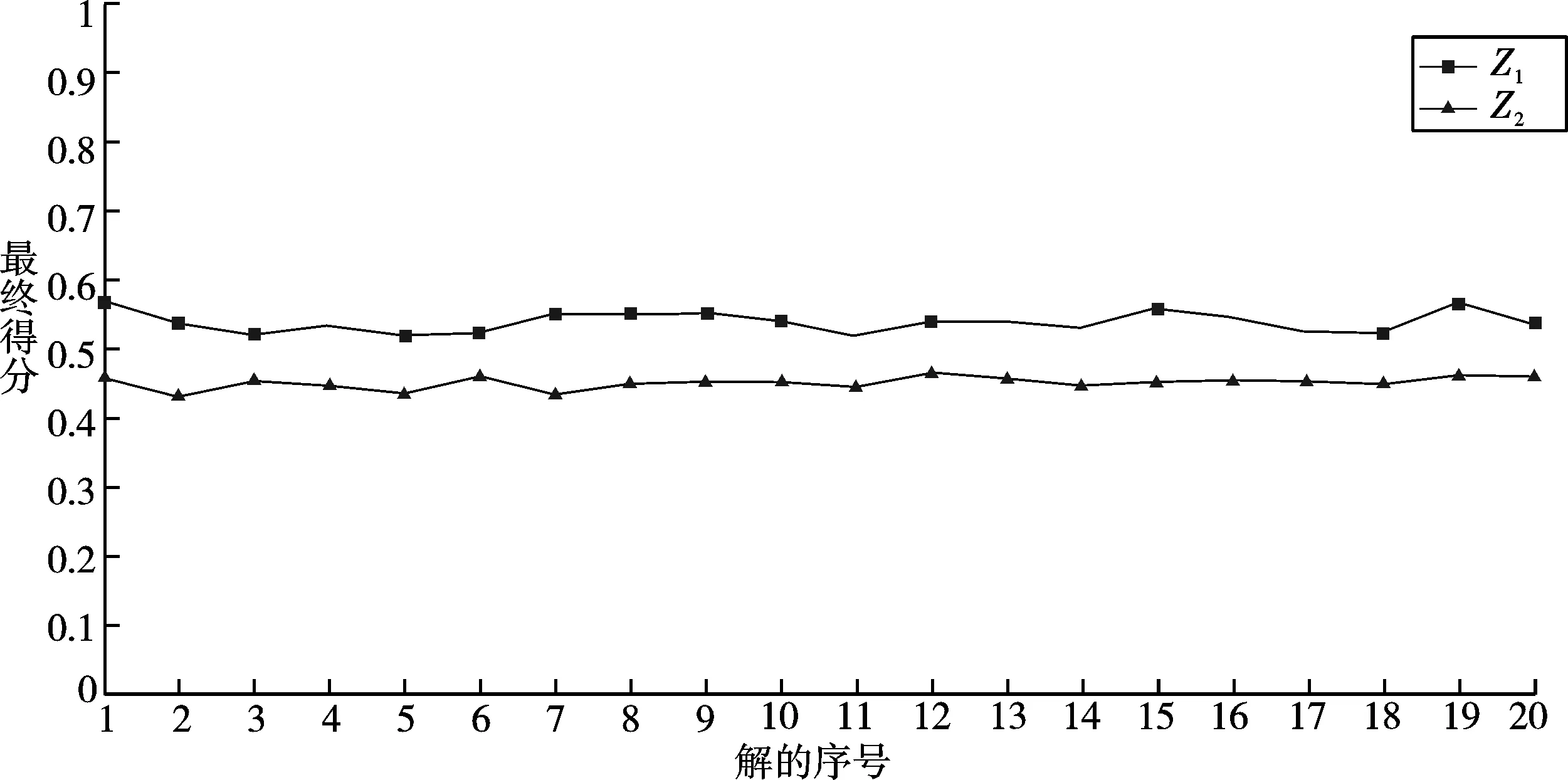
图1 Z1、Z2最终聚合分值的变化趋势Fig.1 The change trend of the final aggregation scores for Z1 and Z2

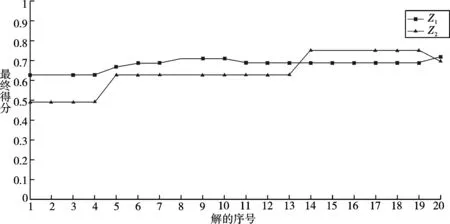
图2 X1、X2最终聚合分值的变化趋势Fig.2 The change trend of the final aggregation scores for X1 and X2

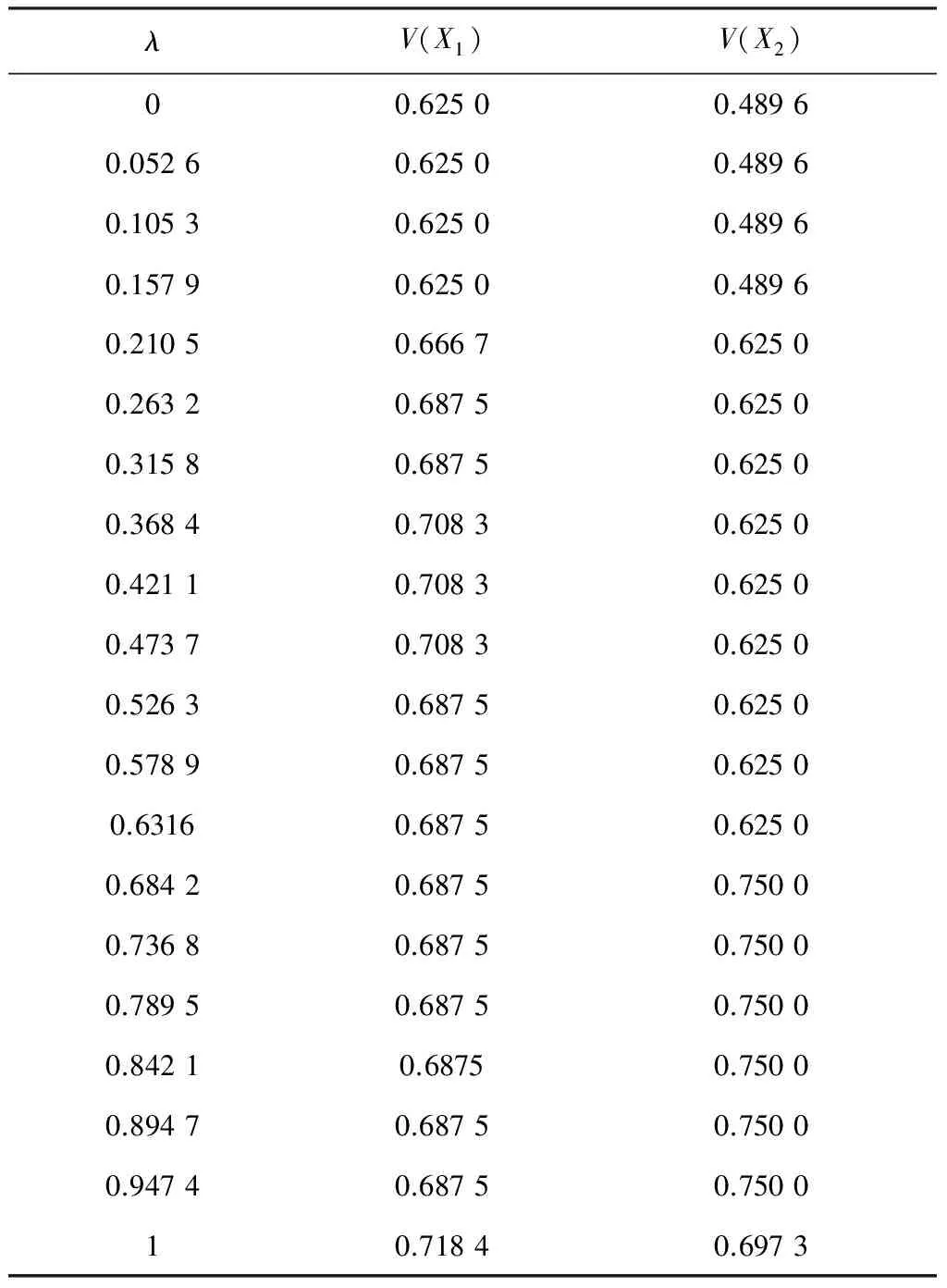
表3 X1、X2的最终聚合分值

4 结语

本文针对绩效评价中评价分数的聚合问题，建立了新的多目标优化模型，并利用遗传算法对模型进行求解。研究结果克服了最近由Andrés等人提出的360度绩效模型所存在的一些不足。数值实验结果表明：本文所采用的方法与文献[6]中的方法相比具有比较明显的优势。值得注意的是如何进一步研究本文所建立的多目标优化模型的一些性质是非常有意义的课题。

[1] DEVRIS D L, MORRISON A M, SHULLMAN S L. Performance Appraisal on the Line[J].Greensboro, NC: Center for Creative Leadership, Technical Report , 1980, 16:1-16

[2] RAYMOND J C. Concise Encyclopedia of Psychology[M]. John & Wiley and Sons Inc, 1987

[3] BRETZ R D, MILKOVICH G T, READ W. The Current State of Performance Appraisal Research and Practice: Concerns, Directions, and Implications[J]. Journal of Management, 1992, 18(2):321-352

[4] 陈正伟. 综合评价技术及应用[M]. 成都: 西南财经大学出版社, 2013

CHEN Z W. Comprehensive Evaluation Technology and Application[M]. Chengdu: Southwestern University of Finance and Economics Press, 2013

[5] 刘思峰, 郭本海, 方志耕. 系统评价:方法、模型、应用[M]. 北京：科学出版社, 2015

LIU S F, GUO B H, FANG Z G. System Evaluation: Methods, Models and Applications[M]. Beijing: Science Press, 2015

[6] ANDRéS R D, GARCíA-LAPRESTA J L, GONZáLEZ-PACHóN J. Performance Appraisal Based on Distance Function Methods[J]. European Journal of Operational Research, 2010, 207(3): 1599-1607

[7] LONDON M, BEATTY R W. 360-degree Feedback as a Competitive Advantage[J]. Human Resource Management, 1993, 32(2-3):353-372

[8] ATWATER L, WALDMAN D. 360 Degree Feedback and Leadership Development[J]. International Journal of Selection and Assessment, 1998, 6(1):35-44

[9] 陆昌勤, 方俐洛, 凌文辁. 360度反馈及其在人力资源管理中的效用[J]. 中国管理科学, 2001, 9(3):74-80

LU C Q, FANG L L, LING W Q. 360 Degree Feedback and Its Application in Human Resource Management[J]. Chinese Journal of Management Science, 2001, 9(3):74-80

[10] 林锉云, 董家礼. 多目标最优化的方法与理论[M]. 吉林: 吉林教育出版社, 1992

LIN C Y, DONG J L. Method and Theory of Multiobjective Optimization[M]. Jilin: Jilin Education Press, 1992

[11] ANTES J, CAMPEN L, DERIGS U, et al. SYNOPSE: A Model-based Decision Support System for the Evaluation of Flight Schedules for Cargo Airlines[J]. Decision Support Systems, 1998, 22(4):307-323

[12] GONZáLEZ-PACHóN J, ROMERO C. Distance-based Consensus Methods: a Goal Programming Approach[J]. Omega, 1999, 27(3):341-347

[13] 杨杰, 方俐洛, 凌文辁. 对绩效评价的若干基本问题的思考[J]. 中国管理科学, 2000, 8(4):74-80

YANG J, FANG L L, LING W Q. Reflections on Some Basic Problems of Performance Evaluation[J]. Chinese Journal of Management Science, 2000, 8(4):74-80

[14] 李志学, 王平心. 建立公平绩效评价的分值转换模型研究[J]. 中国管理科学, 2005, 13(3):126-130

LI Z X, WANG P X. On the Model of Performance Evaluation to Establish a Fair Incentive System[J]. Chinese Journal of Management Science, 2005, 13(3):126-130

[15] BRIEC W, KERSTENS K. Multi-horizon Markowitz Portfolio Performance Appraisals: A General Approach [J]. Omega, 2009, 37(1):50-62

[16] EHRGOTT M. Multicriteria Optimization[M]. Berlin, Heidelberg: Springer, 2005

[17] 赵洁, 陈林, 赵克全. 一类多目标规划问题的混合型对偶[J]. 重庆工商大学学报(自然科学版), 2011, 28(2):145-146

ZHAO J, CHEN L, ZHAO K Q. Mixed Type Duality for a Class of Multi-objective Programming Problems[J]. Journal of Chongqing Technology and Business University (Natural Science Edition) , 2011, 28(2):145-146

Multiobjective Optimization Method of Score Aggregation in Performance Appraisal

LIXi-ting,CHENPei-zhang,ZHAOKe-quan

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

It is of great significance to optimizing the evaluation scores in performance appraisal. There are two stages in the score processing of performance appraisal, including the normalization information phase and the aggregation information phase. In this paper, a new multi-objective optimization model is established based on the aggregation of evaluation scores in performance appraisal, and the model is solved by genetic algorithm. The results of this paper overcome some shortcomings of the 360-degree appraisal model proposed recently by Andrés et al.

performance appraisal; score processing; multiobjective optimization; genetic algorithm

李茜婷 (1988-)，女，重庆市人，硕士研究生，从事多目标优化理论与应用研究.

O221.6