基于固定费用问题的整数规划模型注记*

2017-11-16陈修素

重庆工商大学学报（自然科学版） 2017年6期

关键词：清华大学出版社工商大学运筹学

陈修素，陈睿

( 1.重庆工商大学数学与统计学院,重庆400067; 2.重庆工商大学信息化办公室,重庆 400067)

基于固定费用问题的整数规划模型注记*

陈修素1，陈睿2＊＊

( 1.重庆工商大学数学与统计学院,重庆400067; 2.重庆工商大学信息化办公室,重庆 400067)

分析了运筹学经典教材中整数规划内容里面关于引入0-1变量的实际问题中的一个经典的例子——关于固定费用的问题(Fixed cost Problem)，其建模过程中的一个有待商榷的问题，给出了两种情形的解决方案；并指出了其他部分运筹学教材中的相关问题及其解决思路。

固定费用; 整数规划; 0-1变量；数学模型

由李德和钱颂迪主编的清华大学出版社出版的运筹学[1]自1982年出版以来，深受工科院校从事运筹学教学的老师和学习运筹学的学生们的欢迎和推崇，1990年修订版[2]被国家教委管理工程类专业教材委员会推荐为经济管理类通用教材。经过多年教学过程中的吸收、总结和修改。多次再版[1-4]和多次印刷，印数近百万册，其出版对我国运筹学教学、管理类专业人才的培养以及促进运筹学的研究都有着重要的意义。

在上述运筹学教材的多个版本中都有整数规划中的0-1型整数规划作为一节的内容，在其中首先介绍的是“引入0-1变量的实际问题”，这里面第3个例子是“关于固定费用的问题(Fixed cost Problem)” 。现回忆第一版的运筹学[1]中的该例子的内容如下：

在讨论线性规划时，有些问题是要求使成本为最小．那时总设固定成本为常数，并在线性规划的模型中不必明显列出，但有些固定费用(固定成本)的问题不能用一般线性规划来描述，但可改变为混合整数规划来解决，如例1所示。

例1[1]某工厂为了生产某种产品，有几种不同的生产方式可供选择，如选定的生产方式投资高 (选购自动化程度高的设备)，由于产量大，因而分配到每件产品的变动成本就降低；反之，如选定的生产方式投资低，将来分配到每件产品的变动成本可能增加，所以必须全面考虑。今设有3种方式可供选择，令xj表示采用第j种方式时的产量；cj表示采用第j种方式时每件产品的变动成本；kj表示采用第j种方式时的固定成本。

为了说明成本的特点，暂不考虑其他约束条件。采用各种生产方式的总成本分别为

在构成目标函数时，为了统一在一个问题中讨论，现引入0-l变量yj，令

(1)

于是目标函数：

minz=(k1y1+c1x1)+(k2y2+c2x2)+(k3y3+c3x3)

式(1)这个规定可由下述3个线性约束条件表示：

(2)

式(2)中，M是个充分大的常数，式(2)说明，当xj>0时，yj必须为1；当xj=0时，只有yj为0才有意义，所以式(2)可以完全代替式(1)。

注记1：在该运筹学教材的多个不同的版本中，该例子的介绍除了部分文字和式子的编号略有改动外，其余均无变动。但在上述问题中式(2)是不能完全代替式(1)的，因为由式(2)可知，当xj=0时，yj可以为0，也可以为1。因此式(2)不能完全刻画式(1)规定的要求。为此分情况给出上述问题如下的两种解决方案。

情形1：如果产品的计件单位是整数，即每种生产方式的产品的产量均是整数，此时的模型可以改进如下：

即用

yj≤xj≤yjMj=1,2,3

(3)

代替式(1)，因为由式(3)的右端不等式可知，当xj>0时，yj≠0，从而yj必须为1，且由于xj取值为整数，此时式(3)左端自然成立。当xj=0时，满足式(3)的yj只能为0，由此分析可见，式(3)完全替代了式(1)的要求。

情形2：如果产品的计件单位不是整数，即每种生产方式的产品的产量是非负实数，此时的模型可以改进如下：

其中yj=sgn(xj)表示符号函数。

徐永仁在其编写的《经济管理运筹学》[5]的4.2节“0-1规划问题与隐枚举法”中的第一部分“0-1规划问题”的第4个例子(详见参考文献[5]中的第92页)介绍了通过引入0-1变量y及其中的约束条件式(4)—式(7)来表示带有分段性质的如下目标函数：

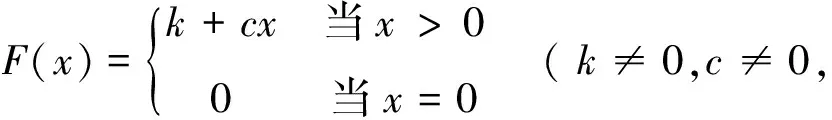
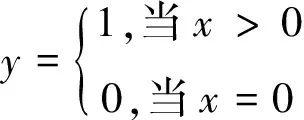
把分段形式的目标函数表示如下带约束条件的线性函数：

F(x)=ky+cx

(4)

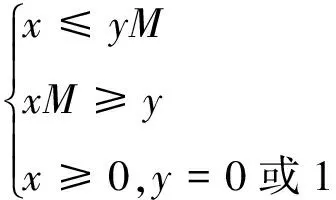
(5)

(6)

(7)

其中M为一个充分大的数。

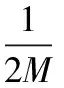
因此，利用式(4)—式(7)是不能表示出例4的分段性质的目标函数的，可以利用前面介绍的方法，分如下两种情形作处理。

当x取值非负整数时，其分段形式的目标函数可表示成如下带约束条件的线性函数：

F(x)=ky+cx

(8)

(12)

(13)

当x取值非负实数时，其分段形式的目标函数可表示为带约束条件的如下线性函数：

F(x)=ky+cx

(11)

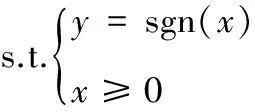
(12)

(13)

西南交通大学的省级精品课程运筹学中的”运筹学A课件”里的整数规划中的第四节 0-1 规划里面的模型实例中的第3例 “固定费用问题”涉及利用3种资源生产3种产品，由于不同产品的生产组织方式不同，生产相应产品的固定费用互不相同，问题是要制定一个使总的净收益最大的生产计划，利用3个0-1变量yj(j=1,2,3),建立了含有3种资源约束的、以总的净收益最大的整数规划模型：

maxz=4x1+5x2+6x3-100y1-150y2-200y3

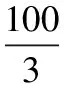
注记3：上述模型中的后面四行约束与第一个案例一样，可以由xj>0导出yj=1，但不能由xj=0导出yj=0，因此上述建模未能解决原问题。如果利用前面情形(1)的解决方法可得该问题如下的线性规划整数模型：

maxz=4x1+5x2+6x3-100y1-150y2-200y3

[1] 《运筹学》试用教材编写组.运筹学[M].12th edt.北京：清华大学出版社,1982

Trial Teaching Material Drawing Board of Operations Research. Operations Research[M]. Beijing: Tsinghua University Press,1982

[2] 《运筹学》教材编写组：运筹学(修订版)[M].2版,北京：清华大学出版社,1990

Teaching Material Drawing Board of Operations Research. Operational Research (Revised Edition)[M].2nd edt, Beijing: Tsinghua University Press, January 1990

[3] 《运筹学》教材编写组.运筹学[M].3版. 北京：清华大学出版社,2005

Teaching Material Drawing Board of Operations Research, Operational Research[M]. 3rd edt. Beijing: Tsinghua University Press,2005

[4] 《运筹学》教材编写组. 运筹学(本科班)[M]. 4版. 北京：清华大学出版社,2005

Teaching Material Drawing Board of Operations Research. Operational Research (Undergraduate Class)[M]. 4th edt, Beijing: Tsinghua University Press, 2005

[5] 徐永仁. 经济管理运筹学[M]. 哈尔滨：哈尔滨工业大学出版社,1996

XU Y R. Operations Research in Economic Management[M]. Harbin: Harbin Industrial University Press, 1996

Notes about Integer Programming Model for Fixed Cost Problems

CHENXiu-su1,CHENRui2

(1. School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China; 2. Information Office, Chongqing Technology and Business University, Chongqing 400067, China)

This paper analyzes the introduction of a classic example in practical problem of 0-1 variables in the integer programming content in the classic textbook of operational research, proposes that fixed cost problem is worth being discussed in the process of modeling, gives the solutions for two kinds of situation and points out the related problems and their solutions in other textbooks of operational research.

fixed cost; integer programming; 0-1 variables; mathematical model

O317