代理模型帮助的SA层性能差分演化优化算法*

杜 欣，吴晓斌+，倪友聪,2，叶 鹏，李 松

1.福建师范大学 软件学院，福州 350117

2.伦敦大学学院 计算机科学学院，英国 伦敦 WC1E 6BT

3.武汉纺织大学 数学与计算机学院，武汉 430200

代理模型帮助的SA层性能差分演化优化算法*

杜 欣1，吴晓斌1+，倪友聪1,2，叶 鹏3，李 松1

1.福建师范大学 软件学院，福州 350117

2.伦敦大学学院 计算机科学学院，英国 伦敦 WC1E 6BT

3.武汉纺织大学 数学与计算机学院，武汉 430200

为了在庞大空间中搜索软件体系结构（software architecture，SA）层最优性能改进方案，当前已涌现出一些以NSGA-II为代表的性能优化算法。然而这些算法大多未充分考虑性能改进空间的离散特性和性能评估的高计算代价特点，导致了解质量不高和优化时间过长的问题。针对这一问题，提出一种代理模型帮助的SA层性能差分演化优化算法SMDE4PO（surrogate model assisted differential evolution algorithm for performance optimization）。该算法采用多种交叉和变异策略以增大搜索空间和提高收敛速度，并运用随机森林作为代理模型以大幅减少实际性能评估的次数。在4个不同规模案例上的实验结果表明：（1）在贡献度、世代距离和超体积3个指标上SMDE4PO显著优于NSGA-II算法；（2）通过使用随机森林代理模型，在最好情况下SMDE4PO较NSGA-II算法的运行时间可降低48%。

软件体系结构；性能优化；差分演化；代理模型

1 引言

软件体系结构（software architecture，SA）在较高抽象层次上描述了构成软件系统的元素以及元素之间的交互关系[1]。基于SA进行性能分析评估[2]，可以尽早地发现资源使用率过高，响应时间过长和吞吐量过小等性能问题，并通过相应的设计改进来缓解或消除这些问题，进而可在软件生命周期的早期达到性能优化的目的。然而随着软件系统的规模越来越大，复杂性越来越高，影响性能的因素也随之增多，使得基于SA的性能改进空间也在不断增大。

文献[3]描述了业务报告系统（business report system，BRS），其初始SA如图1所示。BRS的初始SA包括server1至server4共4台硬件服务器和9个组件。每台服务器的处理器速率（processing rate，PR）都为10.0 GHz。BRS的SA中有处理器速率、组件部署和组件选择3类不同的可变元素（又称自由度）。具体的，4台服务器的PR值可在[5.0,20.0]GHz上变化；而9个组件中的每一个均可部署在4台服务器中的任意1台；此外WebServer组件有可替代组件Web-Server2供选择。因而，BRS的SA共有14个可变元素，且这些元素不同取值都对性能产生复杂的非线性影响。即使每个服务器的PR只考虑取20个可选值，BRS例子中可能的改进方案也将超过839亿。如何在庞大的性能改进空间中获得最优SA已成为学术界和工业界高度关注的研究主题[4]。近年来已涌现出基于规则和基于元启发两类SA层性能的自动优化方法[5]。

基于规则的方法[6-7]将SA层性能改进知识运用机器可处理的规则形式予以描述。规则的条件部分用于诊断性能问题，而动作部分则按一定幅度对可变元素的值进行改进。基于规则的方法还按照一定的策略组合使用预定义的规则以搜索最优性能改进方案。受制于规则预定义的改进幅度和所采用的搜索策略，基于规则的方法往往只能搜索受限的改进空间，常常只能获取局部最优的性能改进方案。而基于元启发的方法则直接对SA中可变元素进行编码以表示出性能改进方案，并进一步设计元启发算法搜索最优性能改进方案。与规则方法相比，元启发方法可以搜索更大的空间，能够获取更优的性能改进方案。最近一些元启发方法还将性能、硬件成本或其他质量属性作为多个目标，并运用NSGA-II算法进行演化优化。然而已有的元启发方法大多未充分考虑以下两个问题：

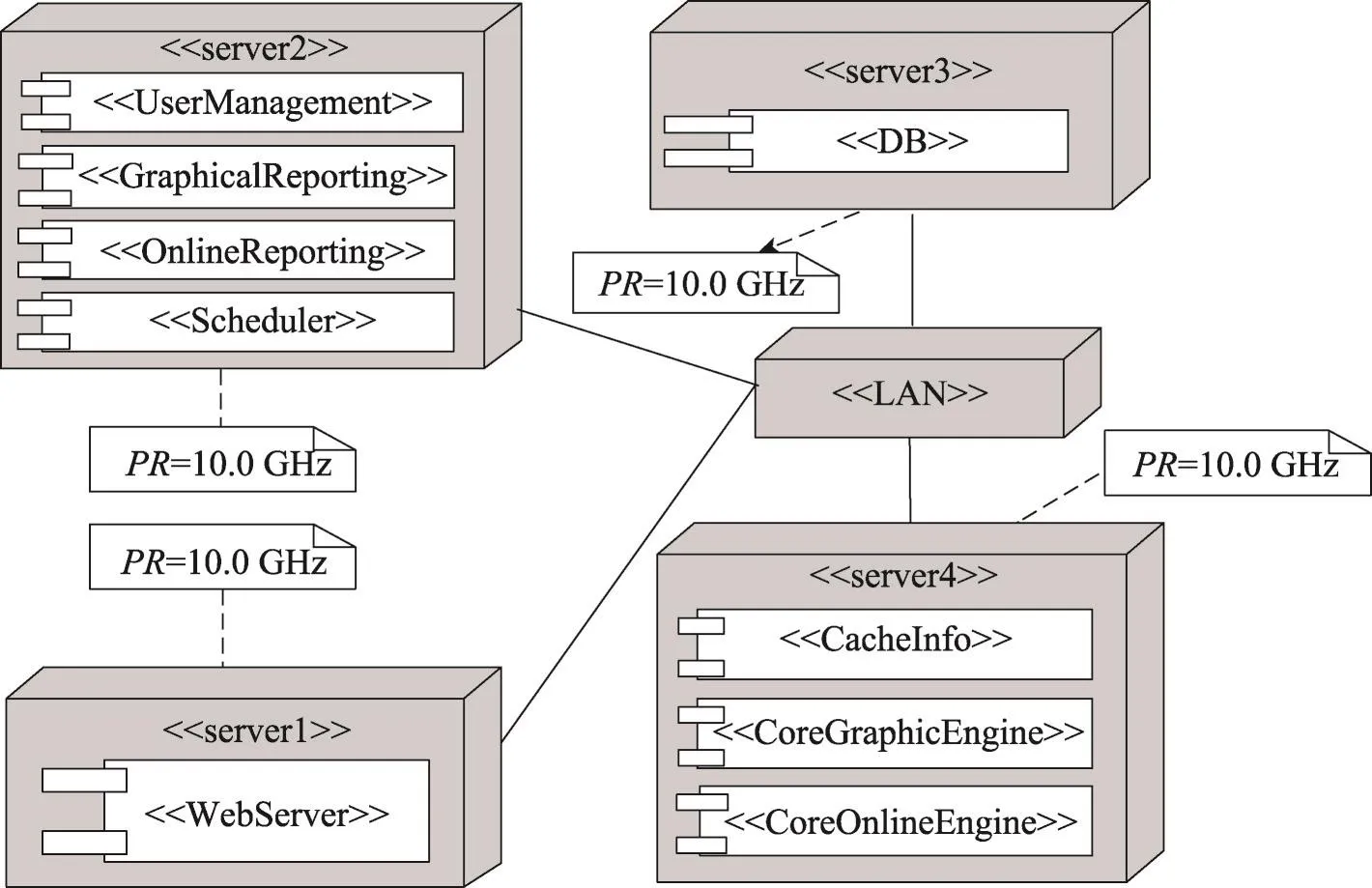
Fig.1 Schematic diagram of initial software architecture of business reporting system图1 业务报告系统的初始软件体系结构

（1）SA中可变元素不仅有不同的取值类型，如数值和类属（category）等，而且还需要满足一定的取值约束和限制。这将导致性能改进空间呈现高度的非连续形态。例如：BRS案例中4台服务器的PR取实数类型的值；而每个组件的部署只能取类属类型的值，即取集合{server1,server2,server3,server4}中的1个元素作为值；对于WebServer组件的取值也是类属类型。此外，BRS例中PR取值在[5.0,20.0]内连续变化；若将组件部署和组件选择的类属类型取值映射到从1开始的整数集，则它们的取值约束分别为[1,4]和[1,2]。因此，性能改进方案的编码将呈现实数和整数混合编码的形式。这给优化算法搜索全局最优解带来一定的困难。

（2）在演化过程中，通过SA性能评估而获取性能指标值（如系统响应时间）是一个高代价和耗时长的计算步骤。在2.66 GHz处理器、2 GB内存及Win8.1操作系统环境下，根据文献[3]迭代200次共评估性能6 000次的参数设定，图2给出了NSGA-II算法的运行时间以及性能评估耗时的对照情况。从图2中可以看出，将近一半的运行时间要用于SA的性能评估。

Fig.2 Running time of NSGA-II algorithm and consuming time of performance evaluation in BRS case图2 BRS案例中NSGA-II算法运行时间与性能评估耗时

针对已有的元启发方法因未充分考虑性能改进空间的离散特性和性能评估的高计算代价特点，而导致解质量不高和优化时间过长的问题，本文提出了一种代理模型帮助的SA层性能差分演化优化算法。主要贡献如下：

（1）通过4个不同规模的案例对多项式回归（polynomial regression，PRS）、Kriging、径向基函数网络（radial basis function network，RBFN）、支持向量机（support vector machine，SVM）与随机森林（random forest，RF）等5种常用的预测模型进行实验对比，实证了RF更加适合用作SA层性能演化优化过程中的代理模型。

（2）设计了一种代理模型帮助的SA层性能差分演化优化算法SMDE4PO（surrogate model assisted differential evolution algorithm for performance optimization）。该算法采用多种交叉和变异策略，并运用RF作为代理模型预估系统响应时间值，以提高解质量，并降低演化时间。

（3）在4个不同规模的案例上与NSGA-II算法进行实验对比，结果表明本文SMDE4PO算法在贡献度、世代距离和超体积3个质量指标上显著优于NSGA-II算法。与此同时，在最好情况下SMDE4PO较NSGA-II算法的运行时间可降低48%。

本文组织结构如下：第2章阐述相关工作；第3章描述SA层性能优化问题；第4章给出差分演化算法SMDE4PO的具体步骤和总体流程；第5章给出案例研究及实验结果；第6章总结全文，并给出未来工作。

2 相关工作

下面简要介绍基于SA层性能评估、基于元启发的SA层性能优化方法及用于演化算法的代理模型等相关工作。

2.1 SA层性能评估

为了能够在设计阶段基于SA进行软件性能评估，人们已提出了排队网（queueing net，QN）[8]、分层排队网（layered queueing net，LQN）[9]、随机Petri网[10]、随机进程代数[11]和马尔可夫链[12]等性能模型及其分析工具，并在此基础上，提出了一些SA层性能评估方法[2]。图3示意了SA层性能评估过程。待建系统的SA经过变换器的变换可生成某种性能模型的一个实例，再通过解析分析器对该性能模型进行处理并输出相应的性能评估报告，最后借助读取器可从评估报告中获取待建系统的各项性能指标（如响应时间、吞吐量和资源使用率等），本文仅讨论系统响应时间。值得注意的是：在SA层性能优化过程中，性能评估是一个计算代价相对较高和耗时相对较长的步骤。

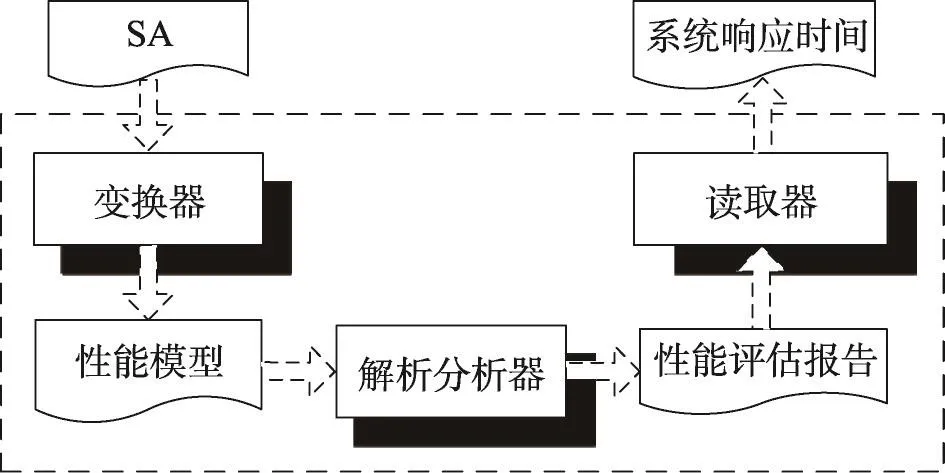
Fig.3 Process of performance evaluation at SAlevel图3 SA层性能评估过程

2.2 基于元启发的SA层性能优化方法

针对不同的SA建模语言，并通过设计不同的元启发算法，人们已提出了一些基于元启发的SA层性能优化方法。

（1）基于PCM（Palladio component model）建模语言，Martens[13]和Saed[14]分别运用爬山算法和粒子群算法优化系统响应时间。Koziolek等人[15]使用NSGA-II算法优化系统的响应时间和硬件成本。Martens等人[16-17]利用NSGA-II算法优化系统的性能、可靠性和硬件成本。

（2）基于 East-AADL（architecture analysis and design language）建模语言，Li等人[18]使用NSGA-II算法优化系统的数据流延迟、处理器使用率和代价。Etemaadi等人[19-22]应用NSGA-II算法优化系统的性能、安全性和硬件成本。Walker等人[23]使用NSGA-II算法优化系统的性能、可信性和硬件代价。

（3）基于AADL建模语言，Meedeniya[24]和Rahmoun等人[25]运用NSGA-II算法优化系统的性能和可靠性。

已有的元启发优化方法可以对单个性能指标进行优化也可以对多个性能指标进行优化，甚至还将性能、硬件成本及其他质量属性作为多个目标进行优化。在多目标性能的元启发优化方法中，NSGA-II往往是它们首选的演化优化算法。

2.3 用于演化算法的代理模型

演化算法在求解复杂的非线性优化问题时，往往需要用很高的代价计算目标函数的值，常常导致求解效率低和演化时间长的问题。通过构建代理模型预估个体的目标函数值，减少演化算法调用目标函数的次数，为解决这一问题提供了一种较好的手段。文献[26-27]指出多项式回归[28]、Kriging[29]、径向基函数网络[30]、支持向量机[31]和随机森林[32]等常被用作演化算法[33-36]的代理模型。

演化算法在运行过程中有3种训练代理模型的控制策略[27]：一是无演化控制策略，仅在初始种群产生之前训练生成代理模型，并在整个演化过程中一直运用代理模型预估目标函数值，而不再训练生成新的代理模型。二是固定的演化控制策略，当预估目标值的个体数或演化代数达到预定义的数目时，重新训练并生成新的代理模型，并用新模型预估个体的目标函数值。三是自适应的演化控制策略，当代理模型的性能下降到预设的下界时，重新训练并生成新的代理模型，并用新模型预估个体的目标函数值。第一种策略[37]更多适用于低维问题，第二种策略[38-39]因能获取良好的性能而得到广泛应用，第三种策略[40]常由于控制过程的复杂性而较少在实际中使用。

3 SA层性能优化问题的描述

下面以系统响应时间和硬件成本为目标，给出SA层性能优化问题的描述。

定义1定义rest(SA)和cost(SA)分别表示根据软件体系结构SA进行性能和成本评估，而获取的系统响应时间和硬件成本的值。

rest(SA)的计算需要对SA进行性能模型的变换、解析和分析，因而计算代价相对较高，计算时间相对较长。本文采用文献[3,15]的方法计算cost(SA)，只需要根据SA中各硬件服务器的处理速率PR值进行计算。

定义2若SA中有D个可变元素，且每个元素可以取一定范围内变化的实数或整数值，则SA层性能优化问题的解X可表示为满足式（1）的D维向量(x1,x2,…,xD)。式（1）中分别表示第j维变量取值的上下界。

可变元素处理器PR值往往取指定范围内的实数。若将组件部署、组件选择等类属类型取值映射到从1开始的整数集，则它们可以取特定范围内的整数。

定义3定义函数genSA(X)表示根据解X定义的各可变元素的值，修改初始软件体系结构SA0而生成的结果软件体系结构。

定义4SA层性能优化可以抽象为式（2）定义的两目标优化问题。式（2）中目标函数f1(X)和f2(X)分别表示根据解X生成的结果软件体系结构，获取系统响应时间和改进代价的值。式（3）和式（4）给出式（2）问题对应的Pareto最优解集Opt。在式（3）和式（4）中，≺和Ω分别表示支配关系和代表解空间。

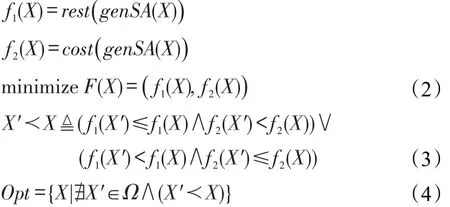
4 代理模型帮助的SA层性能差分演化优化算法SMDE4PO

为了求解式（2）定义的问题，本文基于DEMO（differential evolution for multiobjective optimization）算法[41]提出一种SA层性能差分优化算法SMDE4PO。下面先阐述SMDE4PO算法的主要遗传操作，再给出其总体流程。

4.1 初始化种群

SMDE4PO算法初始化种群中第i个体的编码可按式（5）和式（6）定义的方法进行随机生成。式（5）和式（6）中，xj,i(0)表示第0代初始种群中第i个体的第j维编码。rand(0,1)表示在[0,1]区间产生均匀分布的随机数，而ceil表示上取整函数。实数编码和整数编码的维度可分别按式（5）和式（6）随机生成。

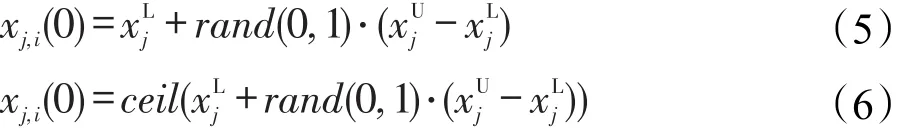
4.2 适应度评估

SMDE4PO算法的适应度评估主要是依据个体编码x获取硬件成本和系统响应时间两个目标值，其过程如图4所示。硬件成本的计算分成两个步骤：首先计算genSA(x)获取结果软件体系结构SA*；然后计算cost(SA*)并输出硬件成本的值。由于计算系统响应时间的代价高，耗时长，SMDE4PO算法引入随机森林代理模型预估系统响应时间。具体的系统响应时间目标值的求解过程由解析阶段、预测阶段，以及这两个阶段之间的转化构成，如图4中3个虚线框所示。

在解析阶段，首先根据结果软件体系结构SA*求解rest(SA*)获取实际的系统响应时间rst*；然后将(x,rst*)作为样本进行收集和存储。当收集的样本超过预定义的数目时，则由解析阶段向预测阶段进行转化。在转化过程中，首先随机森林学习算法被启动，并运用解析阶段采集的样本构建代理模型，然后进入预测阶段。

在预测阶段，个体编码x被输入到随机森林代理模型预测其对应的系统响应时间。当预测次数超过预定义的大小时，预测阶段向解析阶段进行转化。系统响应时间目标值的求解将进入下一个解析阶段并重新收集新的训练样本。

4.3 变异操作

SMDE4PO算法的变异操作分为两个步骤：第一步从预定义的差分策略池中随机选取一种策略对个体编码xi（又称目标向量）进行变异，并生成变异向量vi；第二步对vi的每个分量j进行越界检查，若实数编码部分违反，则依据式（7）进行修复，若整数编码部分违反，则按式（8）修复。

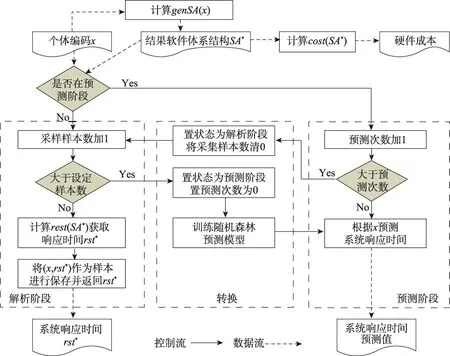
Fig.4 Process for fitness evaluation of SMDE4PO algorithm图4SMDE4PO算法的适应度评估过程

为了防止种群陷入局部搜索，并考虑加快收敛速度，从文献[42]定义的差分策略中选取4种构建SMDE4PO算法的策略池，如表1所示。表1“DE/x/y”中的x和y分别表示目标向量、差分向量的个数。x可以是当前种群中的随机（rand）个体xri、最优（best）个体xb或当前（current）个体xc。xri(g)表示第g代种群中第ri个体，F为缩放因子。

Table 1 Mutation strategies used by SMDE4PO algorithm表1 SMDE4PO算法选用的变异策略

4.4 交叉操作

SMDE4PO算法从预定义的交叉策略池中随机选取一种交叉策略，并对目标向量xi和变异向量vi进行交叉，以生成试验向量ui。交叉策略池是由二项分布和指数分布两种交叉策略所构成的。

式（9）给出了二项分布交叉操作。其中，NP为种群大小，jrand为[1,NP]上的随机整数，CR称为交叉概率，取值范围为[0,1]。而指数分布交叉操作是先在[1,D]上随机产生uj,i(g)的开始交叉位置k，并按图5生成连续交叉的位数l，再依据式（10）和式（11）确定交叉范围[low,high]。ui(g)中在交叉范围内的每个分量置为vj,i(g)，而其他分量则置为xj,i(g)。

Fig.5 Pseudo code for generating cross over bits图5 生成交叉位数的伪代码

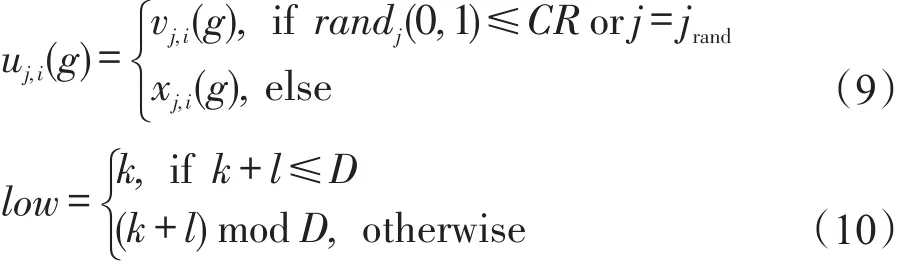
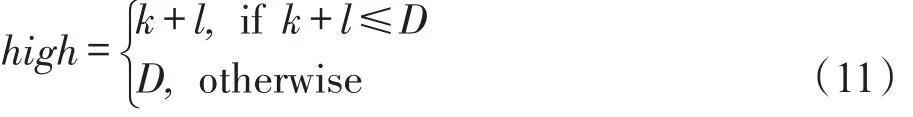
4.5 选择操作

SMDE4PO算法采用式（12）表示贪婪策略选择下一代种群的个体。式（12）中，P͂(g)表示第g代的临时种群，在第g代种群演化前置空。≺表示支配关系，它的含义由式（3）定义。

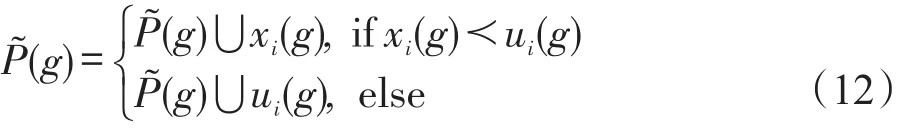
4.6 算法流程

SMDE4PO算法流程如下所示。第12行对临时种群P͂(g)的截断方法与文献[41]相同，都是按非支配等级和拥挤距离进行排序后，从中选取NP（种群大小）个个体。

5 案例研究

为了验证本文SMDE4PO算法的有效性，下面首先给出验证的问题及度量指标；然后简介案例并阐述所使用的统计方法；最后说明实验的安装，并展示实验结果。

5.1 验证研究的问题及度量指标

问题1（RQ1）多项式回归（PRS）、Kriging模型、径向基函数网络（RBFN）、支持向量机（SVM）和随机森林（RF）等5种常用的预测模型哪一种更适合作为SA层性能演化优化算法的代理模型？SMDE4PO算法使用代理模型预估个体的系统响应时间，并作为选择个体的依据。因而代理模型的优劣直接影响到SMDE4PO算法的性能。文献[24-25]综述了用于演化算法的各种代理模型，并指出PRS、Kriging、RBFN、SVM和RF是最常使用的5种代理模型。故SMDE4PO算法重点考虑这5种模型。

为了公平评判各种代理模型，本文考虑SA层性能优化问题的特点和文献[26]评估代理模型的方法，选用训练+预测执行时间（time of execution for training+prediction，TTP）和等级保持（ranking preservation，RP）作为回答RQ1的两个指标。TTP定义为在训练样本数和测试样本数都为100的情况下，代理模型的训练和预测所需的时间总和。RP较TTP复杂，下面先阐述保序性的概念，再具体给出计算方法。

称代理模型对个体x和y的目标值预估具有保序性，当且仅当式（13）定义的h(x,y)为真。在式（13）中，分别是目标函数和预测函数。当预测从1开始顺序编号的N个个体的目标值时，RP值的计算如式（14）和式（15）所示。其中，函数u表示按编号获取对应的个体。从式（14）和式（15）可以看出：RP度量了代理模型在预测的N个个体中有多少对个体具有保序性，并将这个数字规一化到[0,1]区间内。RP值越大说明代理模型越优。

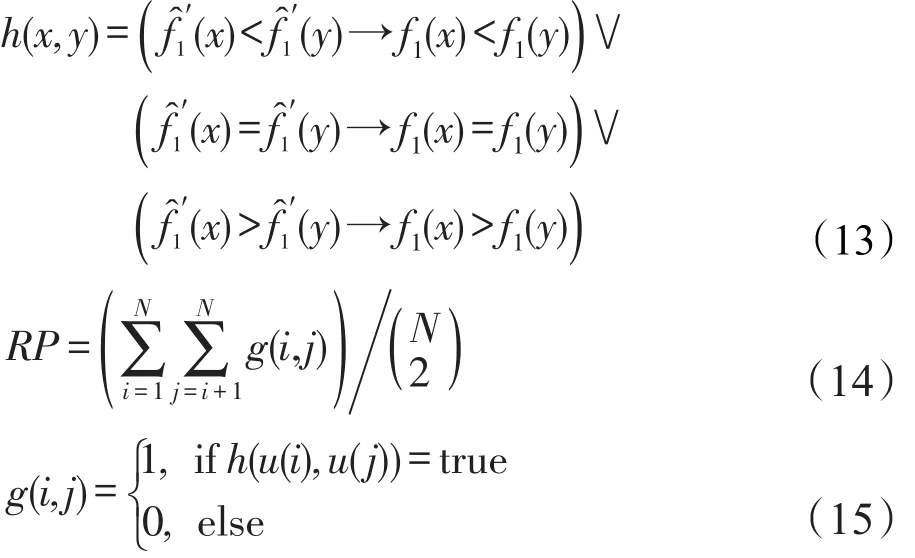
问题2（RQ2）SMDE4PO算法的解质量是否优于NSGA-II算法？NSGA-II算法是目前SA层性能优化采用最多的，同时也是获取较优结果的一种算法。因而通过回答这一问题，以验证SMDE4PO算法的有效性和有用性。

为了定量回答RQ2，本文使用贡献度（contribution）、世代距离（generational distance）和超体积（hyper volume）3个指标，并依次将它们简记为IC、IHV和IGD。在说明IC、IHV和IGD之前，先假设 SMDE4PO和NSGA-II算法求出的Pareto解集分别为S1和S2，且这两个解集对应的参考Pareto解集为RS（对S1和S2的并集求取非支配解集）。

IC指标[43]用于度量S1和S2对RS的贡献度。IC指标值在[0,1]之间变化，其值越大说明对RS贡献越多。IHV指标[44]用于度量S1和S2在目标空间中所覆盖的超体积。IHV值在[0,1]之间变化，其值越大说明在目标空间中支配其他解的数目也越多。IGD指标[45]用于度量S1和S2与RS在目标空间中的接近程度。为了使IGD与IC、IHV具有相同的取值范围和优劣变化的方向，将文献[45]的指标值进行反向并归一化到[0,1]。本文定义的IGD指标如式（16）所示。其中d(x,y)表示解x和y在目标空间中的欧氏距离，而|RS|表示RS中解的个数。IGD越大说明解集Si与RS在目标空间中越接近。IC、IHV和IGD的值越大，表明解质量越优。

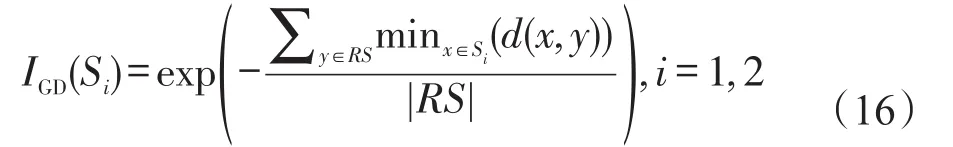
问题3（RQ3）在获取更高质量解的前提下，SMDE4PO算法较NSGA-II算法是否显著降低了运行时间？通过这一问题进一步验证代理模型引入的合理性和有效性。

5.2 案例简介

商业报告系统BRS[3]、多媒体文件存取系统MS[46]、过程控制系统PCS[47]和简单设计策略例子STE（https://svnserver.informatik.kit.edu/i43/svn/code/Palladio/Examples/SimpleHeuristicsExample）被用作回答RQ1、RQ2和RQ3的案例。表2给出了这4个案例的规模。从表2中可以看出，规模从大到小依次是PCS、BRS、MS和STE，这与各案例可变元素的数目一致。此外，经对比可变元素的取值范围，发现各案例性能改进空间的大小与它们的规模大小也是一致的。

5.3 使用的统计方法

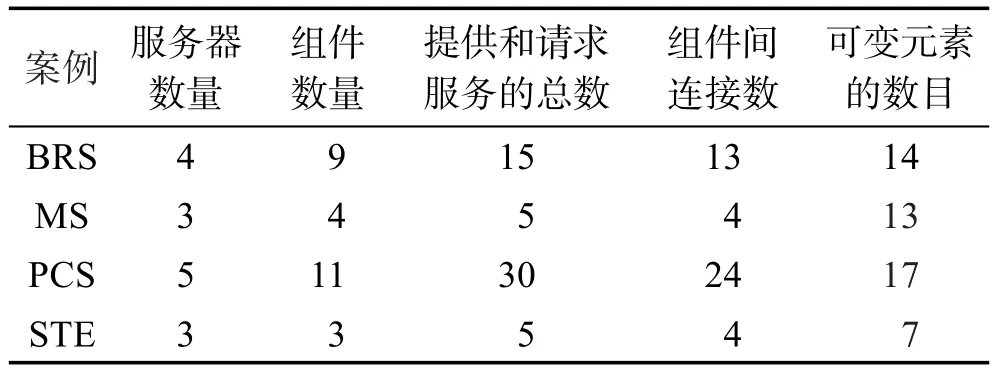
Table 2 Scale of BRS,MS,PCS and STE cases表2 BRS、MS、PCS和STE案例的规模

本文采用Wilcoxon秩和检验对实验数据进行统计分析，并将置信水平α的值设为0.05。Wilcoxon秩和检验能够给出对比数据在统计学上显著的差异性。为了进一步观测差异程度的大小（effect size），本文采用Vargha-Delaney[48]的作为 effect size的直观度量。的值域为[0,1]，其值越大说明差异程度越大。

5.4 实验安装

（1）代理模型训练参数的设定

为了避免因模型参数设定不当而导致评价有失公平，在表3设定的参数范围内训练各个模型并取测试中平均平方误差（mean squared error，MSE）最小的模型作为参与比较的模型。

（2）算法参数的设定

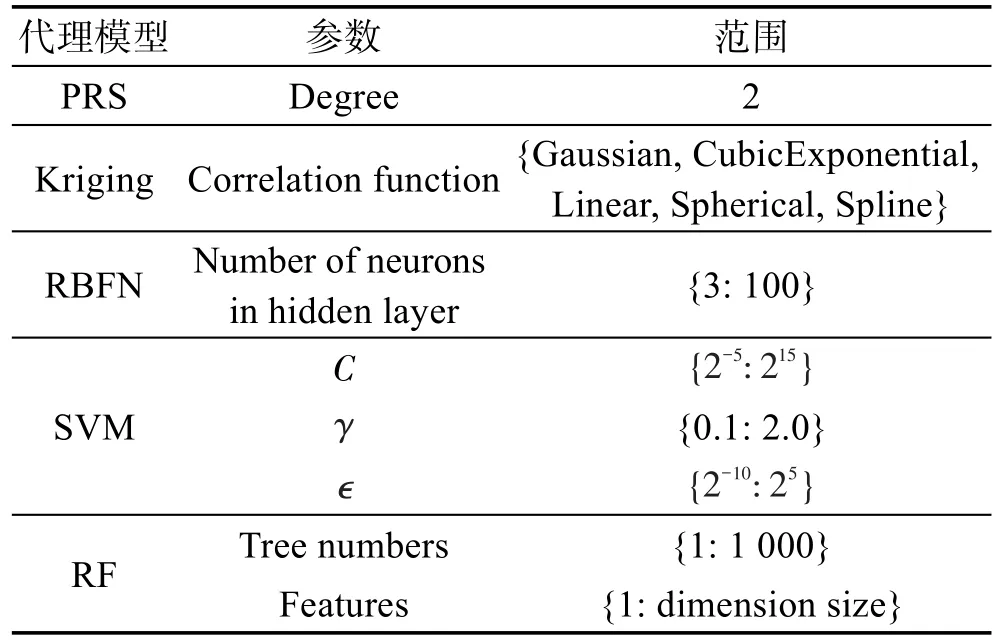
Table 3 Value or range of parameters used to train surrogate model in SMDE4PO algorithm表3 SMDE4PO算法代理模型训练参数及范围设定

表4给出NSGA-II和SMDE4PO两种算法的参数设定，为了公平起见，这两种算法每次运行过程中个体评估次数都为6 000次。对每个案例，NSGA-II和SMDE4PO算法都独立运行30次。

（3）实验过程

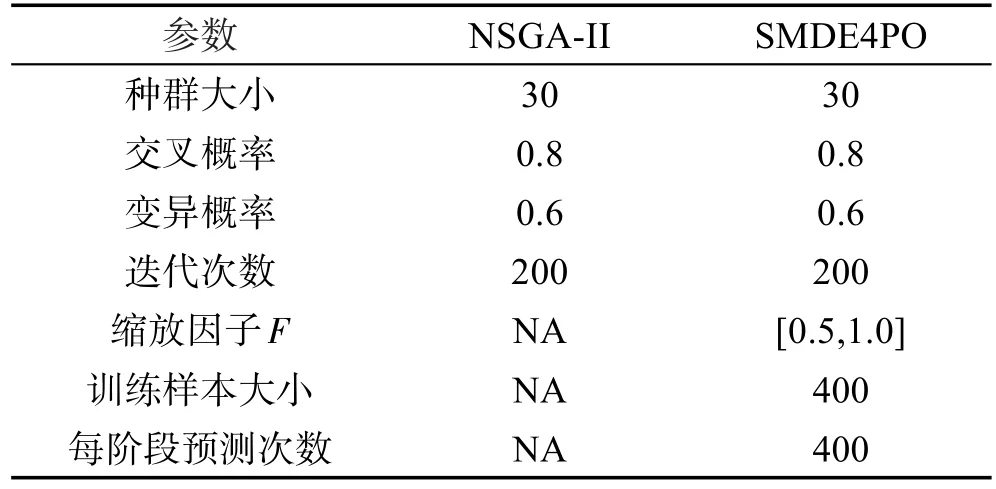
Table 4 Parameters setting in NSGA-II and SMDE4PO algorithms表4 NSGA-II和SMDE4PO算法参数设定

实验过程可按下面的4个步骤进行。

步骤1对每个案例按照拉丁超立方体抽样的思想生成200个解，并通过性能评估获取这些解对应的系统响应时间。将每个解及其对应的系统响应时间作为一个样本，则每个案例可生成包含200个样本的数据集。BRS、PCS、MS和STE案例共生成4个数据集。

步骤2根据步骤1生成的每个数据集，与文献[24]一样，先随机均匀抽取100个样本作为训练样本并将剩下样本作为测试样本；再按照表4设定的参数范围对PRS、Kriging、RBFN、SVM和RF模型分别进行训练，记录最优模型下RP值和TTP值，并进行统计分析，回答RQ1。

步骤3 针对各个案例（BRS、PCS、MS和STE），按表5的参数设置独立运行NSGA-II和SMDE4PO算法各30次，记录每次运行所获取的Pareto最优解集和所消耗的时间。

步骤4根据步骤3记录的结果，先计算NSGA-II和SMDE4PO算法的解质量指标IC、IHV和IGD；再对IC、IHV、IGD和运行时间分别进行统计分析后回答RQ2和RQ3。

5.5 实验结果

在Intel®CoreTM2 2.66 GHz处理器、2 GB内存及Win8.1操作系统实验环境下，按上一节阐述的方法安装和运行实验，并完成实验数据的收集和相关图表的绘制。下面具体给出3个问题RQ1、RQ2和RQ3的实验结果。

（1）RQ1的结果

表5显示了BRS、MS、PCS和STE案例下5种模型PRS、Kriging、RBFN、SVM和RF在最优训练参数下获取的等级保持RP、训练和预测运行时间TTP两个指标的值。从表5中可以看出，对所有的4个案例，RF的RP和TTP值优于其他4个模型。

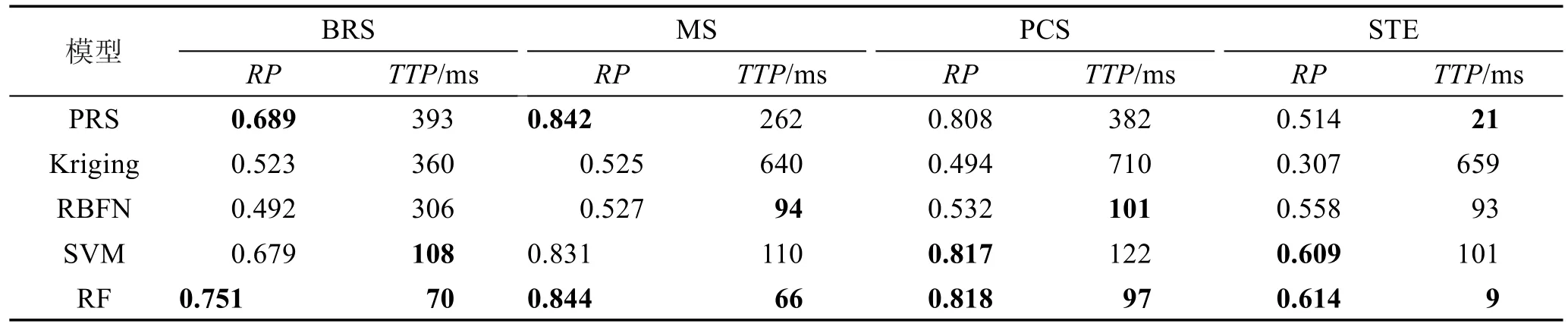
Table 5 Measure of TTP and RP applied to PRS,Kriging,RBFN,SVM and RF models in BRS,MS,PCS,and STE cases表5 PRS、Kriging、RBFN、SVM和RF模型在BRS、MS、PCS和STE案例下的RP和TTP值

为了便于比较，除了对表5中RF行对应的最优RP和TTP值进行了加粗标记外，还加粗标出了各案例中第二优的RP和TTP值。具体地，在BRS、MS、PCS和STE案例中，RF的RP值较第二优的RP值分别提高了8.3%、0.2%、0.1%和0.8%；而RF的TPP值较第二优的TPP值分别降低了35.2%、29.8%、4.0%和57.1%。这一实验结果表明，RF较PRS、Kriging、RBFN和SVM模型更适合作为SA层性能演化优化算法的代理模型。

（2）RQ2的结果

表6显示了BRS、MS、PCS和STE案例下NSGAII和SMDE4PO算法的IC、IGD和IHV指标的秩和实验结果。从表6中p-value值可以看出，SMDE4PO算法的IC、IGD和IHV指标显著优于NSGA-II算法。这一结论与统计盒图6观测的结果是一致的。表7显示了IC、IGD和IHV指标对应的effect size的大小。从表7中可以得出两个结论：一是在所有案例上，IC指标的effect size都为1，这说明SMDE4PO算法总能获取一些两个目标值均优于NSGA-II的解；另一是BRS和PCS对应的IGD和IHV指标的effect size优于MS和STE，这说明在案例规模和性能改进空间较大时，SMDE4PO算法获取的解集较NSGA-II算法不仅更加接近于参考Pareto解集，并且能够覆盖更多解空间。

Table 6 p-value obtained in Wilcoxon experiments applying NSGA-II and SMDE4PO algorithms to BRS,MS,PCS and STE cases表6 BRS、MS、PCS和STE案例下NSGA-II和SMDE4PO算法的Wilcoxon实验对应的p-value值

（3）RQ3的结果

表8和图7显示了BRS、MS、PCS和STE案例下NSGA-II和SMDE4PO算法运行30次的平均耗时情况。从表8和图7中可以看出，BRS和PCS的耗时较MS和STE长，说明案例的规模和性能改进空间越大，NSGA-II和SMDE4PO算法的耗时也越长。另外，从表8中可以看出SMDE4PO算法较NSGA-II算法耗时降低的比例，从PCS案例的43%到BRS案例的48%。这一实验结果表明：运用代理模型可以有效地减少性能评估的次数，进而能够大幅地降低运行时间。

6 结论和未来工作

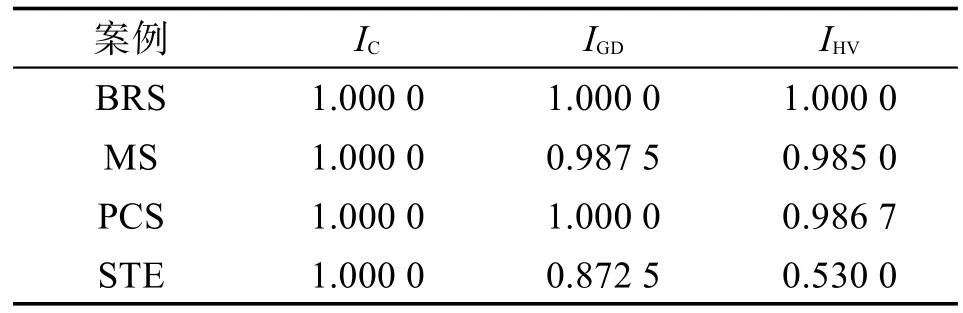
Table 7 Effect size obtained in Wilcoxon experiments applying NSGA-II and SMDE4PO algorithms to BRS,MS,PCS and STE cases表7 BRS、PCS、MS和STE案例下NSGA-II和SMDE4PO算法的Wilcoxon实验对应的effect size值

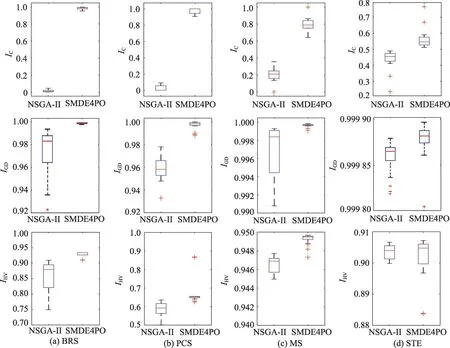
Fig.6 Boxplots of IC,IGD,and IHVapplying NSGA-II and SMDE4PO algorithms in BRS,PCS,MS and STE cases图6 BRS、PCS、MS和STE案例下NSGA-II和SMDE4PO算法的IC、IGD和IHV盒图

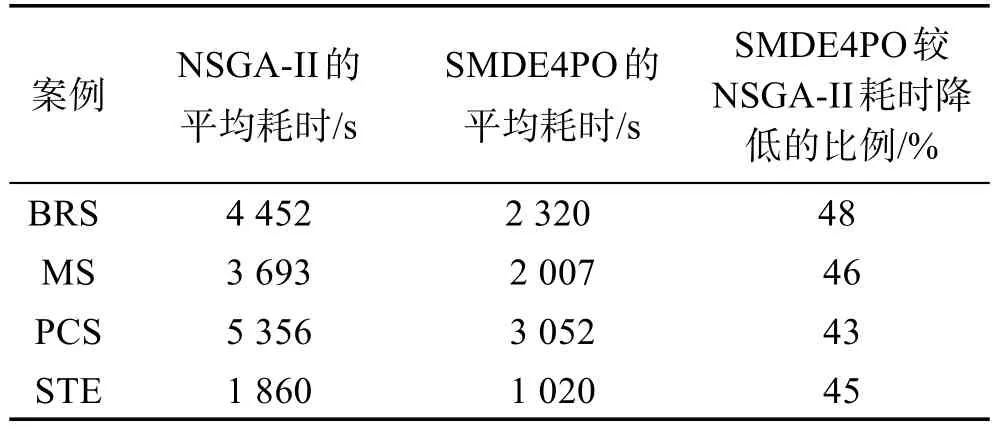
Table 8 Average consuming time between NSGA-II and SMDE4PO algorithms by 30 runs in BRS,PCS,MS,and STE cases表8 BRS、MS、PCS和STE案例下NSGA-II和SMDE4PO算法运行30次的平均耗时

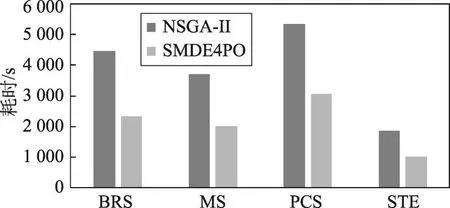
Fig.7 Time-consuming comparison between NSGA-II and SMDE4PO algorithms in BRS,MS,PCS and STE cases图7 BRS、MS、PCS和STE案例下NSGA-II和SMDE4PO算法耗时对比

本文提出了一种SA层性能差分演化优化算法SMDE4PO。SMDE4PO算法采用多种交叉和变异策略增大搜索空间和提高收敛速度，以期在离散解空间中获取高质量的解。SMDE4PO算法还引入随机森林作为代理模型预估性能指标，以解决因SA层性能评估的计算代价大而导致优化时间长的问题。与NSGA-II算法在4个不同规模案例上的实验结果表明，SMDE4PO算法在显著降低运行时间的同时，能够有效地提高解的质量。未来将扩展本文算法同时优化性能、硬件成本、可用性和可靠性等多个质量属性，以提出一种代理模型帮助的软件体系结构演化优化方法。

[1]Taylor R N,Medvidovic N,Dashofy E M.Software architecture:foundations,theory,and practice[M].New York:Wiley Publishing,2009:471-472.

[2]Brosig F,Meier P,Becker S,et al.Quantitative evaluation of model-driven performance analysis and simulation of component-based architectures[J].IEEE Transactions on Software Engineering,2015,41(2):157-175.

[3]Koziolek A,Ardagna D,Mirandola R.Hybrid multi-attribute QoS optimization in component based software systems[J].Journal of Systems&Software,2013,86(10):2542-2558.

[4]Aleti A,Buhnova B,Grunske L,et al.Software architecture optimization methods:a systematic literature review[J].IEEE Transactions on Software Engineering,2013,39(5):658-683.

[5]Koziolek A.Automated improvement of software architecture models for performance and other quality attributes[M].Karlsruhe:KIT Scientific Publishing,2014.

[6]Du Xin,Ni Youcong,Ye Peng,et al.An evolutionary algorithm for performance optimization at software architecture level[C]//Proceedings of the 2015 IEEE Congress on Evolutionary Computation,Sendai,Japan,May 25-28,2015.Piscataway,USA:IEEE,2015:2129-2136.

[7]Du Xin,Ni Youcong,Ye Peng.A multi-objective evolutionary algorithm for rule-based performance optimization at software architecture level[C]//Proceedings of the 2015 Genetic and Evolutionary Computation Conference,Madrid,Spain,Jul 11-15,2015.New York:ACM,2015:1385-1386.

[8]Kounev S.Performance modeling and evaluation of distributed component-based systems using queueing Petri nets[J].IEEE Transactions on Software Engineering,2006,32(7):486-502.

[9]Tribastone M.A fluid model for layered queueing networks[J].IEEE Transactions on Software Engineering,2013,39(6):744-756.

[10]Distefano S,Scarpa M,Puliafito A.From UML to Petri nets:the PCM-based methodology[J].IEEE Transactions on Software Engineering,2010,37(1):65-79.

[11]Tribastone M,Gilmore S,Hillston J.Scalable differential analysis of process algebra models[J].IEEE Transactions on Software Engineering,2010,38(1):205-219.

[12]Koziolek A,Ardagna D,Mirandola R.Hybrid multi-attribute QoS optimization in component based software systems[J].Journal of Systems&Software,2013,86(10):2542-2558.

[13]Martens A,Koziolek H.Automatic,model-based software performance improvement for component-based software designs[J].Electronic Notes in Theoretical Computer Science,2009,253(1):77-93.

[14]Saed A A,Kadir W M N W.Applying particle swarm optimization to software performance prediction an introduction to the approach[C]//Proceedings of the 5th Malaysian Conference in Software Engineering,Johor Bahru,Malaysia,Dec 13-14,2011.Piscataway,USA:IEEE,2011:207-212.

[15]Koziolek A,Koziolek H,Reussner R H.Peropteryx:automated application of tactics in multi-objective software architecture optimization[C]//Proceedings of the 7th International Conference on the Quality of Software Architectures and 2nd International Symposium on Architecting Critical Systems,Boulder,USA,Jun 20-24,2011.New York:ACM,2011:33-42.

[16]Martens A,Koziolek H,Becker S,et al.Automatically improve software architecture models for performance,reliability,and cost using evolutionary algorithms[C]//Proceedings of the 1st Joint WOSP/SIPEW International Conference on Performance Engineering,San Jose,USA,Jan 28-30,2010.New York:ACM,2010:105-116.

[17]Reussner R.Domain-specific heuristics for automated improvement of PCM-based architectures[D].Karlsruhe:University of Karlsruhe,2010.

[18]Li Rui,Etemaadi R,Emmerich M T M,et al.An evolutionary multiobjective optimization approach to componentbased software architecture design[C]//Proceedings of the 2011 IEEE Congress on Evolutionary Computation,New Orleans,USA,Jun 5-8,2011.Piscataway,USA:IEEE,2011:432-439.

[19]Etemaadi R,Chaudron M R.Varying topology of componentbased system architectures using metaheuristic optimization[C]//Proceedings of the 38th Euromicro Conference on Software Engineering and Advanced Applications,Izmir,Turkey,Sep 5-8,2012.Washington:IEEE Computer Society,2012:63-70.

[20]Etemaadi R,Lind K,Heldal R,et al.Quality-driven optimization of system architecture:industrial case study on an automotive sub-system[J].Journal of Systems&Software,2013,86(10):2559-2573.

[21]Etemaadi R.Quality-driven multi-objective optimization of software architecture design:method,tool,and application[D].Leiden:Leiden University,2014.

[22]Etemaadi R,Chaudron M R.New degrees of freedom in metaheuristic optimization of component-based systems architecture:architecture topology and load balancing[J].Science of Computer Programming,2015,97:366-380.

[23]Walker M,Reiser M O,Tucci-Piergiovanni S,et al.Automatic optimisation of system architectures using EAST-ADL[J].Journal of Systems&Software,2013,86(10):2467-2487.

[24]Meedeniya I,Aleti A,Avazpour I,et al.Robust archeopterix:architecture optimization of embedded systems under uncertainty[C]//Proceedings of the 2nd International Workshop on Software Engineering for Embedded Systems,Zurich,Switzerland,Jun 9,2012.Piscataway,USA:IEEE,2012:23-29.

[25]Rahmoun S,BordeE,Pautet L.Automatic selection and composition of model transformations alternatives using evolutionary algorithms[C]//Proceedings of the 2015 European Conference on Software Architecture Workshops,Dubrovnik/Cavtat,Croatia,Sep 7-11,2015.New York:ACM,2015:25.

[26]Díaz-ManríquezA,Toscano-Pulido G,Gómez-Flores W.On the selection of surrogate models in evolutionary optimization algorithms[C]//Proceedings of the 2011 IEEE Congress on Evolutionary Computation,New Orleans,USA,Jun 5-8,2011.Piscataway,USA:IEEE,2011:2155-2162.

[27]Díaz-Manríquez A,Toscano-Pulido G,Barron-Zambrano J H,et al.A review of surrogate assisted multi-objective evolutionary algorithms[J].Computational Intelligence&Neuroscience,2016,4:1-14.

[28]Box G E P,Wilson K B.On the experimental attainment of optimum conditions[M]//Breakthroughs in Statistics.New York:Springer-Verlag,Inc,1992:270-310.

[29]Matheron G.Principles of geostatistics[J].Economic Geology,1963,58(8):1246-1266.

[30]Babu G S,Suresh S.Sequential projection-based metacognitive learning in a radial basis function network for classification problems[J].IEEE Transactions on Neural Networks&Learning Systems,2013,24(2):194-206.

[31]Cortes C,Vapnik V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.

[32]Breiman L.Random forests[J].Machine Learning,2001,45(1):5-32.

[33]Mallipeddi R,Lee M.An evolving surrogate model-based differential evolution algorithm[J].Applied Soft Computing,2015,34(C):770-787.

[34]Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[35]Ciccazzo A,Pillo G D,Latorre V.A SVM surrogate modelbased method for parametric yield optimization[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2016,35(7):1224-1228.

[36]Akhtar T,Shoemaker C A.Multi objective optimization of computationally expensive multi-modal functions with RBF surrogates and multi-rule selection[J].Journal of Global Optimization,2016,64(1):17-32.

[37]Husain A,Kim K Y.Enhanced multi-objective optimization of a microchannel heat sink through evolutionary algorithm coupled with multiple surrogate models[J].Applied Thermal Engineering,2010,30(13):1683-1691.

[38]Isaacs A,Ray T,Smith W.An evolutionary algorithm with spatially distributed surrogates for multiobjective optimization[C]//LNCS 4828:Proceedings of the 3rd Australian conference on Progress in Artificial Life,Gold Coast,Australia,Dec 4-6,2007.Berlin,Heidelberg:Springer,2007:257-268.

[39]Jin Yaochu.A comprehensive survey of fitness approximation in evolutionary computation[J].Soft Computing,2005,9(1):3-12.

[40]Gaspar-Cunha A,Vieira A.A multiobjective evolutionary algorithm using neural network to approximate fitness evaluations[J].International Journal of Computers,Systems&Signals,2005,6:18-36.

[41]Robič T,Filipič B.DEMO:differential evolution for multiobjective optimization[C]//LNCS 3410:Proceedings of the 2005 International Conference on Evolutionary Multi-Criterion Optimization,Guanajuato,Mexico,Mar 9-11,2005.Berlin,Heidelberg:Springer,2005:520-533.

[42]Mendes R,Mohais A S.DynDE:a differential evolution for dynamic optimization problems[C]//Proceedings of the 2015 IEEE Congress on Evolutionary Computation,Edinburgh,UK,Sep 2-4,2005.Piscataway,USA:IEEE,2005:2808-2815.

[43]Meunier H,Talbi E G,Reininger P.A multiobjective genetic algorithm for radio network optimization[C]//Proceedings of the 2000 Congress on Evolutionary Computation,La Jolla,USA,Jul 16-19,2000.Piscataway,USA:IEEE,2000:317-324.

[44]Zitzler E,Thiele L.Multiobjective evolutionary algorithms:a comparative case study and the strength Pareto approach[J].IEEE Transactions on Evolutionary Computation,1999,3(4):257-271.

[45]Van Veldhuizen D A,Lamont G B.Multiobjective evolutionary algorithm research:a history and analysis[J].Evolutionary Computation,1999,8(2):125-147.

[46]Brosch F,Buhnova B,Koziolek H,et al.Reliability prediction for fault-tolerant software architectures[C]//Proceedings of the Joint ACM SIGSOFT Conference-ISARCS on Quality of Software Architectures-QoSA and Architecting Critical Systems,Boulder,USA,Jun 20-24,2011.New York:ACM,2011:75-84.

[47]Koziolek H,Schlich B,Bilich C,et al.An industrial case study on quality impact prediction for evolving service-oriented software[C]//Proceedings of the 33rd International Conference on Software Engineering,Honolulu,USA,May 21-28,2011.New York:ACM,2011:776-785.

[48]Goulden K J.Effect sizes for research:a broad practical approach[J].Journal of Developmental&Behavioral Pediatrics,2006,27(5):419-420.

2016-09,Accepted 2016-11.

Surrogate Model Assisted Differential Evolutionary for Performance Optimization at SALevel*

DU Xin1,WU Xiaobin1+,NI Youcong1,2,YE Peng3,LI Song1
1.Faculty of Software,Fujian Normal University,Fuzhou 350117,China
2.Department of Computer Science,University College London,London,WC1E 6BT,UK
3.College of Mathematics and Computer,Wuhan Textile University,Wuhan 430200,China
+Corresponding author:E-mail:a1072466135@163.com

A few of evolutionary algorithms for performance optimization at software architecture(SA)level have been proposed to obtain the near optimal performance improvement solutions in large search space,and the NSGAII is the typical representative of these algorithms.However,most of these algorithms do not fully consider two factors:the performance improvement space with discrete feature and the performance evaluation with the high computational effort.As a result,the solutions obtained by these algorithms are not good and the corresponding processes of performance optimization are also considerably time-consuming.Aiming at this problem,this paper proposes a surrogate model assisted differential evolution algorithm for performance optimization at SA level,which is named by SMDE4PO.In the SMDE4PO,many strategies of crossover and mutation are adopted to enlarge the search space and accelerate the convergence.Furthermore,the random forest is regarded as surrogate model to substantially reduce the number of performance evaluation.The experimental results from four different size of cases show that(1)The SMDE4PO is significantly better than the NSGA-II in three indicators of contribution,generation distance and hyper volume;(2)By means of the random forest to predict performance indices,the run time of the SMDE4PO is reduced by 48%than the NSGA-II in the best results in the experiments.

software architecture;performance optimization;differential evolution;surrogate model

10.3778/j.issn.1673-9418.1609032

*The National Natural Science Foundation of China under Grant Nos.61305079,61370078(国家自然科学基金);the Natural Science Foundation of Fujian Province under Grant No.2015J01235(福建省自然科学基金);the JK Project of the Education Department of Fujian Province under Grant No.JK2015006(福建省教育厅JK类项目);the Open Fund of State Key Laboratory of Software Engineering of Wuhan University under Grant No.SKLSE 2014-10-02(武汉大学软件工程国家重点实验室开放基金).

CNKI网络优先出版:2016-11-11,http://www.cnki.net/kcms/detail/11.5602.TP.20161111.1627.006.html

DU Xin,WU Xiaobin,NI Youcong,et al.Surrogate model assisted differential evolutionary for performance optimization at SAlevel.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1733-1746.

A

TP311

DU Xin was born in 1979.She received the Ph.D.degree from Wuhan University in 2010.Now she is an associate professor and M.S.supervisor at Fujian Normal University.Her research interests include search-based software engineering and evolutionary computing,etc.

杜欣（1979—），女，新疆石河子人，2010年于武汉大学获得博士学位，现为福建师范大学软件学院副教授、硕士生导师，主要研究领域为基于搜索的软件工程，演化计算等。

WU Xiaobin was born in 1991.He is an M.S.candidate at Fujian Normal University.His research interest is searchbased software design.

吴晓斌（1991—），男，安徽安庆人，福建师范大学硕士研究生，主要研究领域为基于搜索的软件设计。

NI Youcong was born in 1976.He received the Ph.D.degree from Wuhan University in 2010.Now he is an associate professor and M.S.supervisor at Fujian Normal University.His research interests include search-based software design and software architecture,etc.

倪友聪（1976—），男，安徽肥西人，2010年于武汉大学获得博士学位，现为福建师范大学软件学院副教授、硕士生导师，主要研究领域为基于搜索的软件设计，软件体系结构等。

YE Peng was born in 1976.He is a lecture at Wuhan Textile University.His research interests include search-based software design and software architecture,etc.

叶鹏（1976—），男，湖北武汉人，武汉纺织大学数学与计算机学院讲师，主要研究领域为基于搜索的软件设计，软件体系结构等。

LI Song was born in 1993.He is an M.S.candidate at Fujian Normal University.His research interest is searchbased software design.

李松（1993—），男，湖北广水人，福建师范大学硕士研究生，主要研究领域为基于搜索的软件设计。