电子现金协议研究综述*

李舟军，张江霄，冯春辉，隋春荣

1.北京航空航天大学 软件开发环境国家重点实验室，北京 100191

2.邢台学院 数学与信息技术学院，河北 邢台 054001

电子现金协议研究综述*

李舟军1，张江霄2+，冯春辉2，隋春荣2

1.北京航空航天大学 软件开发环境国家重点实验室，北京 100191

2.邢台学院 数学与信息技术学院，河北 邢台 054001

随着互联网的快速发展，电子商务的规模越来越大，电子现金（e-cash）作为电子商务的一种重要支付方式，吸引了国内外很多学者对其进行研究，并设计出具有条件性、可分性、可传递性和多银行性的电子现金协议，因此如何设计出安全的具有各个特性的电子现金协议是一个非常重要的研究课题。介绍了电子现金协议的基本模型；从电子现金协议的四个特性出发，介绍了具有各个特性电子现金协议的定义、发展现状和存在问题，并给出每个特性在电子现金协议中的应用场景；分析了构造电子现金协议所需要的重要的密码学原语，以及证明了电子现金协议安全的可证明安全理论；最后综述了电子现金协议存在的问题，同时探讨了电子现金协议的最新研究方向。

电子商务；电子现金协议；标准模型；零知识证明；匿名性；区块链

1 引言

现实货币作为人们进行交换的一种基础媒介，可以被用来购买商品、货物等，具有方便、及时等特点。随着互联网的普及，电子商务壮大起来，从而导致多种电子支付方式的兴起，虽然方便了电子商务，但是电子支付普遍存在很大缺陷：（1）在支付过程中银行必须在线，银行成为快速频繁交易的瓶颈；（2）很多电子支付不是匿名的，随时可以查询进行这笔交易的用户身份，导致电子商务信息的泄露。随着网络信息安全的加强，越来越多的人重视个人隐私，而电子支付在电子商务中的无隐私性，即想要查询某人在哪个时段进行了哪方面的交易，直接造成交易双方的隐私泄露。另外，网络购物的热潮，也使得电子支付的使用越来越频繁，其中银行是同时进行大量电子支付的瓶颈所在。

电子现金是现实货币的电子对应物，是能克服以上缺点的一种电子支付方式，利用电子现金，可以很方便地完成在线交易。一个完整的电子现金协议的一般模型由取款协议、花费协议和存款协议三个子协议组成，包括用户、商家和银行三类参与者。首先，用户从银行提取电子现金；然后，用户为获得商品，向商家花费该电子现金；最后，商家把电子现金存入银行。一般电子现金模型如图1。

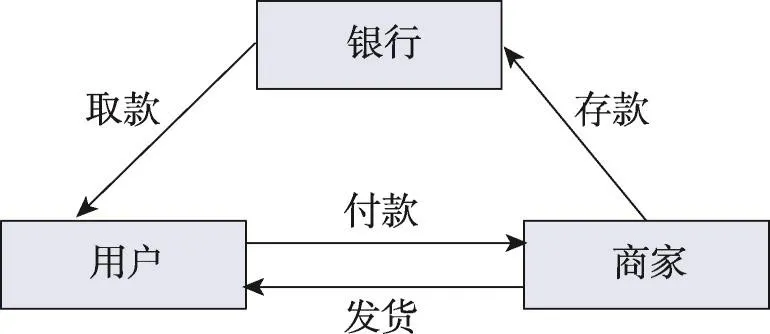
Fig.1 Model of e-cash protocol图1 电子现金协议模型

电子现金协议根据银行在花费协议中是否在线，分为在线的电子现金协议和离线的电子现金协议。其中在线的电子现金协议的安全性虽然高，但是当同时有大量的、频繁的交易时，银行往往成为电子支付的支付瓶颈，因此对于在线电子现金协议的研究不多。离线的电子现金协议，允许花费协议中银行无需参与，这就减少了银行的计算量和通信量，也就避开了在线电子现金协议所存在的问题。为了保证用户的隐私，电子现金协议还具有另一个重要的基本属性——匿名性，该属性保证了恶意的攻击者、商家和银行的联合，他们都无法知道该电子现金的花费情况。这就保证了花费用户的隐私性。

特别是电子现金所具有的离线性和匿名性，使得电子现金的应用受到了人们的重视。为了能更好地应用电子现金，一般从四个特性来进行电子现金协议的研究，即条件性、可分性、可传递性和多银行性。其中的条件性允许用户和商家基于某个未知结果的条件，根据条件结果进行最终的花费；可分性保证了用户对小于已提取电子现金的任意面额的花费性；可传递性保证了商家在收到用户花费的电子现金时，无需存入银行，就可以直接花费该电子现金；多银行性仿照了现实货币的情况，允许电子现金可以在多个银行之间进行流通。以上的四个特性，都是为了在保证电子现金离线性和匿名性的前提下，对电子现金协议的扩展，使得电子现金能更好地实现现实货币的功能。

安全性是电子商务的一个基础保障，也是电子现金协议的一个重要衡量标准，一个完整的电子现金协议应具有以下基本的安全属性：匿名性、不可伪造性、不可重复花费性和不可诬陷性。匿名性是最基础的一种安全属性；不可伪造性是指用户、恶意的攻击者和商家的联合，用户也无法花费多于所提取的电子现金总额；不可重复花费性保证了用户、恶意的攻击者和商家的联合，用户无法花费同一个电子现金两次；不可诬陷性是指银行和恶意攻击者联合，也无法诬陷诚实用户发生了重复花费。

如果设计的电子现金协议不安全，再好的特性也是没有用的。因此电子现金协议被构建后，还需要从安全证明的角度来证明协议所具有的安全性，常用的安全证明模型是随机预言机模型和标准模型。其中的随机预言机模型，把哈希函数看作真正的随机函数，借助它来证明电子现金协议的安全性；而标准模型无需随机预言机假设，直接把攻击者攻破电子现金协议的某个安全属性归约到一个困难问题上，只要攻击者解决了该困难问题，也就攻破了电子现金协议的某个安全属性。由于标准模型下证明的合理性，基于标准模型下证明安全的电子现金协议才是最安全的电子现金协议。

本文首先围绕电子现金协议的四大安全特性，从各个安全特性的定义出发，介绍具有某个安全特性的电子现金协议的发展现状，并综述该安全特性对应的模型，同时指出具有该安全特性的电子现金协议的最新研究成果，分析存在的问题，并提出一些建设性的解决方法。然后概述电子现金协议的安全性证明的两大安全模型，并给出基于标准模型下的电子现金协议的最新研究成果。最后指出电子现金协议的最新发展方向。

2 四个安全特性的电子现金协议研究现状

第一个电子现金协议由Chaum[1]在1983年提出，为了更好地模拟现实中的货币，电子现金应具有以下四个安全特性：条件性、可分性、可传递性和多银行性。下面分别针对电子现金的四个安全特性，来介绍电子现金的国内外研究现状。

2.1 条件电子现金协议

条件电子现金协议具有条件性，条件性是指基于某个未知结果的条件，用户向商家花费该电子现金，只有在条件结果公布后，猜对正确条件结果的一方（用户/商家）才可以从银行提取该电子现金；所构建的电子现金协议可以被应用到很多新的场景。如：在线赌博系统，假设用户1和用户2进行在线赌博，用户1认为事件A是正确的，但是用户2认为事件A是错误的，此时就可以利用条件电子现金来保证，当事件A的正确性在公布后，只有一个用户才能获胜，获得相应的赌金。云计算中的外包计算问题也可以利用条件电子现金来保证，在外包计算中，工人和计算的拥有者之间是互不信任的，工人不相信在工作完成后，拥有者会付承诺的佣金，同样拥有者也不相信在付承诺的佣金后，工人的计算是否完整，并符合要求。条件电子现金协议的模型如图2所示。

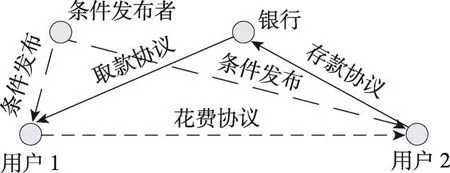
Fig.2 Model of conditional e-cash图2 条件电子现金模型

2007年Shi等人[2]首次引入条件电子现金的概念，并构建了第一个条件电子现金协议。为了提高条件电子现金协议的效率，Blanton[3]在2008年提出了一个高效的条件电子现金协议。Carbunar等人[4]借助条件电子现金的模型，解决了云计算中工人和计算拥有者之间的不信任问题。2010年Li等人[5]考虑了基于多条件的条件传递电子现金，从而用户可以在基于多个条件的情况下花费条件电子现金，提高了条件可传递电子现金的实用性。2011年Carbunar等人[6]考虑了云计算中的公平付费问题，利用该协议，用户和外包者之间就不用担心付费问题，从而实现云计算中的公平付费。2012年张江霄等人[7]构建了一个匿名的条件电子现金协议，该条件电子现金协议解决了Blanton[3]遗留的公开问题，同时条件电子现金协议的效率很高。Chen等人[8]在2013年也构建了一个具有可传递性的条件电子现金协议。2015年张江霄等人[9]引入新的框架，构建了一个具有最优匿名性的条件电子现金协议，并在标准模型下给出了协议的安全性证明。2016年Haddad等人[10]构建了一个条件的多付费协议，该协议考虑了用户的消费计划，利用条件性来满足用户的个人消费计划。

通过上面分析，可知条件电子现金条件性有很广泛的应用场景，迫切需要研究如何构建一个高效、安全、匿名的条件电子现金协议，为达到这个目标，需要进一步改进条件模型，只有条件模型合理了，才能构建出一个高效的条件电子现金协议。

2.2 可分电子现金协议

可分电子现金协议允许用户可以花费小于等于所提取电子现金的任意面额。可分性是电子现金最重要、最基础的一个特性，现存的可分电子现金协议一般都是利用一棵二叉树来实现，二叉树的根节点表示最大的面额，即用户从银行提取的最大面额的电子现金，二叉树的叶子节点代表最小面额的电子现金，即单位电子现金1，二叉树中的任何孩子节点所代表的电子现金总额是其父亲节点的一半。图3是一棵面额为8的二叉树。

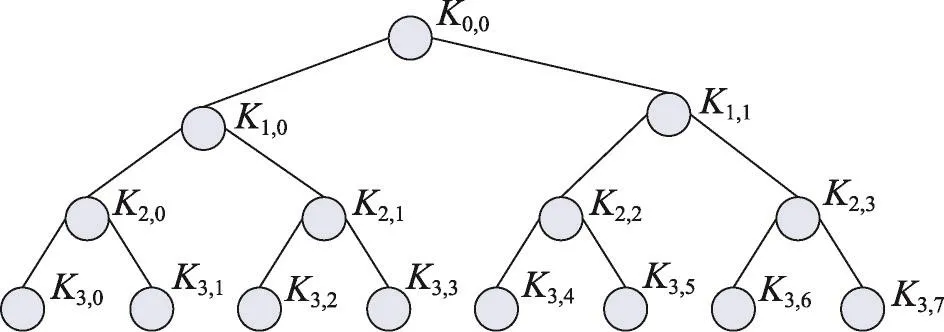
Fig.3 Binary tree with denomination of 8图3 面额为8的二叉树

1991年Okamoto等人[11]构建了第一个可分电子现金协议。Eng等人[12]在1994年基于典型的二叉树结构，构建了一个单条可分电子现金协议，在计算节点的序列号时，从二叉树的叶子节点开始计算，从而减少了用户和银行之间的交互次数。但是用户花费一个电子现金所需要的计算量和电子现金的总额成比例，因此可分电子现金的效率不高。随后，在1995年Okamoto[13]又提出了一个有效的可分电子现金协议，该协议利用位承诺协议，基于大整数分解的困难问题，构建了一个有效的可分电子现金协议。但是该协议的开户效率很低，即用户为了进行取款协议，首先要从银行申请一个一次性的电子牌照，在用户申请电子牌照的过程中，效率是很低的。1998年Chan等人[14]针对Okamoto所构造电子现金开户效率低的问题，构建了一个实用的可分电子现金协议，首先基于离散对数假设，构建了一个有限范围承诺，提高了开户协议的效率，从而在整体上提高了可分电子现金协议的效率。但是该协议中用户花费的电子现金是可链接的。陈凯等人[15]基于概率的方法构建了一个可分电子现金协议。为了满足电子现金协议的不可链接性，Nakanishi等人[16]构建了一个具有不可链接性的电子现金协议，该协议基于群签名协议[17]，使得用户花费的电子现金是不可链接的。但在基于零知识证明的签名证明过程中，使用了切割选择算法，导致该协议的效率比较低。为了撤销重复花费用户的身份，该可分电子现金协议使用了一个可信第三方，诚实用户的身份也可以被可信第三方恢复出来。

为了设计第一个无可信第三方的可分电子现金协议，Camenisch等人[18]在2005年基于CL签名协议，构建了第一个无可信第三方的可分电子现金，但是用户在花费一个价值为N的电子现金时，需要执行N次花费协议，虽然达到了可分性，但是协议的整体效率很低。彭冰等人[19]基于零知识证明和强RSA构建了一个可分电子现金协议。为了进一步提高可分电子现金协议的效率，2007年Canard等人[20]构建了一个真正匿名的可分电子现金协议，该协议使用了CL签名和二叉树，但是由于用户在向银行证明自己花费路径的正确性时，利用了零知识证明技术，从二叉树的根节点逐层证明花费路径的正确性，所需的计算量是很大的，因此协议的效率不高。利用累加器原理，Au等人[21]在2008年构建了一个高效的可分电子现金协议，从而用户在花费协议中，可以直接证明用户花费的正确性，提高了花费协议的效率。由于在花费协议中用户没有证明自己花费路径的正确性，因此该协议中用户存在一定的欺骗概率，可以花费多于所提取的电子现金，即该电子现金系统安全性不具有不可伪造性。2008年陈恺等人[22]构建了一个可撤销的可分电子现金协议。2009年，刘文远等人[23]基于新的二叉树结构，构建了一个可直接计算的可分电子现金协议，该协议基于二叉树和节点可直接计算技术，但是为了证明用户花费的正确性，所需的计算量仍然很大。为了保证可分电子现金协议的安全性，Canard等人[24]构建了一个具有不可伪造性的可分电子现金协议。但是以上所有的可分电子现金协议都是基于随机预言机模型的，现存的一些协议在随机预言机模型下证明是安全的，但是无法在实际中进行实例化，因此Belenkiy等人[25]构建了第一个在标准模型下证明安全的电子现金协议。在2012年Izabachène等人[26]构建了第一个标准模型下证明安全的可分电子现金协议。2013年张江霄等人[27]利用新的签名协议，构建了一个高效的可分电子现金协议。2014年张江霄等人[28]引入了一个新的二叉树结构，基于新的结构，构建了一个标准模型下证明安全的可分电子现金协议。2015年Canard等人在标准模型下，构建了有效的可伸缩的可分电子现金协议[29]和实用的可分电子现金协议[30]。2016年Yang等人[31]构建了一个实用的、匿名的、适合移动设备的可分电子现金协议，该协议利用可信区域，构建一个花费协议效率比较高的可分电子现金协议。

综上所述可知，可分电子现金协议的可分性是电子现金一个最基础的属性，但是可分电子现金协议的效率一般都很低，为了在标准模型下，构建高效的、匿名的无可信第三方的电子现金协议，就需要进一步优化可分电子现金所基于的二叉树模型，只有二叉树模型优化了，才能进一步提高取款协议、花费协议和存款协议的执行效率。

2.3 可传递的电子现金协议

可传递的电子现金协议允许商家在收到用户所花费的电子现金后，无需联系银行，就可以直接把该电子现金花费给其他用户。因此，可传递电子现金协议减少了用户和银行之间的通讯次数，降低了银行的计算量，其基本模型如图4所示。

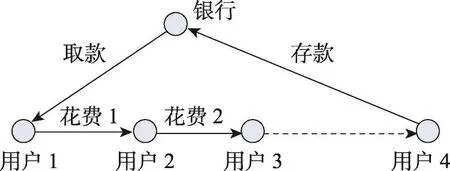
Fig.4 Model of transferable e-cash图4 可传递电子现金模型

Kamoto等人[11]在1991年构建了第一个实用的电子现金协议，该协议具有可传递性。Antwerpen[32]首次对可传递的电子现金给出一般的描述，该描述适合于构建一大类电子付费协议。1991年Okamoto等人[33]构建了一个理想的不可追踪的电子现金协议，该协议具有可分性、可传递性、匿名性等；虽然Okamoto等人构建的可传递的电子现金协议都具有匿名性，但是都只是弱匿名性。1992年Chaum等人[34]分析了可传递电子现金协议的本质，并得出结论：电子现金的长度与用户传递的次数成正比。正因为这个缺点，在很长时间内，可传递的电子现金协议没有进展。但是随着密码学原语的发展，Canard等人[35]在电子现金的存储量和用户与银行的交互次数之间找到了一个平衡，构建了两个可传递的电子现金协议。2008年Canard等人[36]又分析了可传递电子现金协议的匿名性，认为可传递电子现金协议的匿名性和具有其他安全属性的电子现金的匿名性不同，并把可传递电子现金所具有的匿名性称为最优匿名性，即同时具有完美匿名性、最优匿名性1和最优匿名性2。以上所有的可传递电子现金协议都在标准模型下给出了安全证明。基于Groth-Sahai的非交互式零知识证明[37]，Fuchsbauer等人[38]构建了一个常量大小的可传递的电子现金协议。为了解决Fuchsbauer等人[38]遗留的问题，Blazy等人[39]在2011年构建了一个具有最优匿名性的可传递电子现金协议，并在标准模型下给出了协议的安全性证明。2015年张江霄等人[40]引入了花费链构建法，基于新的构建法，在标准模型下给出了一个具有最优匿名性的长度不变的可传递电子现金协议。为了实现 全匿名的可传递电子现金协议，张江霄等人[41]在TASE2015上构建了一个全匿名的可传递电子现金协议。在2015年PKC（International Workshop on Public Key Cryptography）上，Baldimtsi等人[42]构建了一个无可信第三方的完全匿名的可传递电子现金协议。

针对以上问题，为构建一个传递长度是等长的、高效的和匿名的可传递电子现金协议，需要使用可更新签名协议，使得在电子现金传递过程中，可更新电子现金的签名和零知识证明等，以形成一个高效的、等长的和全匿名的可传递电子现金协议。

2.4 多银行电子现金协议

多银行电子现金协议允许用户和商家可以在多个银行开账户，在提取电子现金后，用户向商家花费该电子现金。最后，商家把该电子现金存入银行，由于存在多个银行，用户提取电子现金的银行，与商家存入电子现金的银行很可能是不相同的。多银行电子现金协议的模型如图5所示。

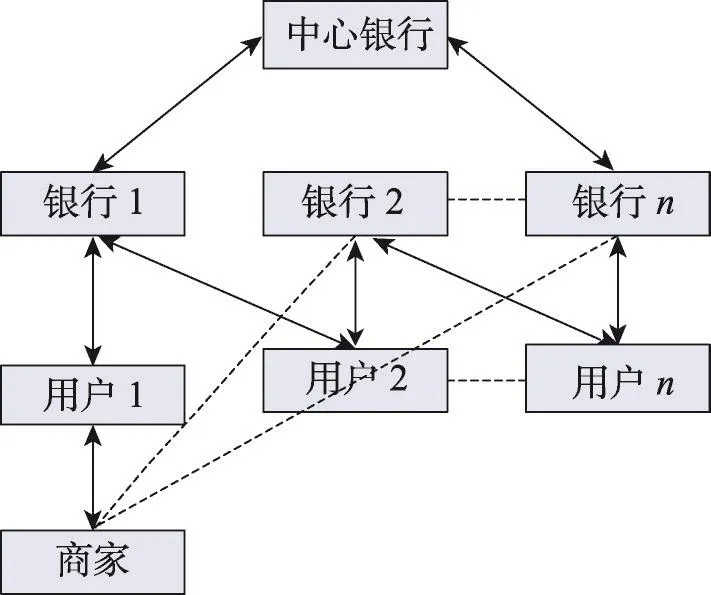
Fig.5 Model of multiple-bank e-cash图5 多银行电子现金模型

1998年Lysyanskaya等人[43]首次引入了多银行电子现金的概念。为了满足公平性，Jeong等人[44]在2000年实现了一个具有公平性的多银行电子现金协议，并指出多银行电子现金协议与一般的电子现金协议的匿名性是不同的，多银行电子现金协议的匿名性不仅包括用户匿名性，还包括银行匿名性，从而更好地保护用户的隐私。2008年Wang等人[45]构建了一个多银行电子现金协议，但是该协议不具有不可伪造性。为了进一步提高Wang等人[45]多银行电子现金协议的安全性，Chen等人[46]在2012年构建了一个满足不可伪造性的多银行电子现金协议。2013年张江霄等人[47]在标准模型下构建了一个多银行电子现金协议。

多银行电子现金协议的构建是为了方便用户存取，更好地模拟现实中的电子现金，这需要一个高效的群盲签名协议，以便为构建高效的多银行电子现金协议，提供坚实的理论基础。

3 常用的密码学原语

电子现金协议很复杂，一般包括取款子协议、花费子协议和存款子协议，为了完成电子现金协议，需要很多密码学原语，下面给出常用的密码学原语。

（1）零知识证明

零知识证明即zero-knowledge proof，是由Goldwasser等人[48]在1985年提出的，指的是证明者不向验证者提供任何有用信息的前提下，验证者能相信证明者能证明某个论断是正确的，如证明者在不泄露私钥的情况下，向验证者证明自己知道某个公钥的私钥。它分为交互式零知识证明和非交互式零知识证明。由于交互式零知识证明的效率比较低，现在基本利用非交互式零知识证明作为构造电子现金协议的基本密码学原语。常用的非交互式零知识证明是Groth-Sahai（GS）证明[37]，具体描述如下：

在标准模型下给出有关双线性群中等式的非交互式零知识证明，它适合多种双线性群中群元素关系的等式，具体包括双线性乘积等式、多标量乘法等式和二次等式，其中基于SXDH（symmetric external Diffe-Heuman）假设下的双线性乘积等式最常用，如下：

给出χ1,χ2,…,χn,Αi∈G1,y1,y2,…,yn,Βi∈G2,t3∈G3,γi,j∈Zn。下面给出双线性等式：

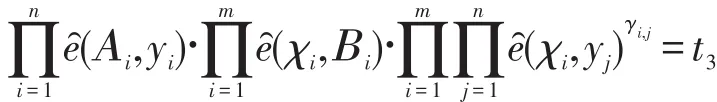
然后利用双线性乘积等式给出证明，最后证明者发送变量承诺以及相关的证明给验证者，验证者就可以验证所给的变量是否满足双线性等式。

在电子现金协议中，一个电子现金经常由序列号、安全序列号和零知识证明组成，零知识证明可以在不泄露电子现金信息的前提下，证明电子现金是正确的，如由银行签发的。

（2）盲签名

盲签名是由Chaum[49]在1982年提出的，消息者先将签名的消息盲化，再由签名者对盲化的消息进行签名，但是签名者并不知道所签的消息具体是什么，最后消息者得到签名的消息。为了便于构造电子现金，它被演化成多种盲签名，如群盲签名、自同态盲签名等。自同态盲签名[50]是一个结构保存签名，即被签名消息、验证密钥和签名都是由群元素组成的，从而该盲签名可以与GS证明完美结合。

在电子现金协议中，电子现金由银行签发并进行盲签名，既保证了电子现金的盲化性，又允许银行对电子现金进行签发。

（3）安全多方计算协议

安全多方计算协议由Yao[51]在1982年提出，当两个或者更多方参与到一起，在保护各自秘密输入的前提下，完成这个计算或者问题。基于安全多方计算，可以实现基于多方的匿名的电子投票系统，从而在保证投票方身份和投票内容保密的前提下，完成投票，也可以被用来构建匿名的电子拍卖系统等。

4 电子现金协议的可证明理论

为了在理论上证明电子现金协议的安全性，需要对所构建的电子现金协议进行安全性分析，最早的安全分析方法是启发式分析。这种安全分析方法假设利用现有最强的攻击方法都无法破解方案，因此在现有计算条件下，不存在一个能够破解该方案的攻击者。但是启发式分析方法只能考查密码方案对已知攻击手段或方法的抵抗能力，而不能确保先前所不知道的攻击手段或方法是否能够破解该方案。为了解决上述问题，可证明安全理论应运而生。

可证明安全理论[52]以计算复杂度理论和概率论为基础，通过归约的方式对协议的安全性证明给出一个有效变换，从而将攻击转变成一个计算复杂性理论中困难问题的重大突破，并分析归约成功的概率。可证明安全首先确定某个方案应满足的安全目标，然后根据攻击者的能力构建一个安全模型，并且定义它对该方案的安全性，最后利用归约方式对攻击者攻破协议的可能性进行具体的概率分析。

可证明安全的思想起源于1984年Goldwasser和Micali等学者的开创性工作，他们提出了语义安全的定义，将概率引入了密码学[53]。粗略地说，可证明安全理论是一种“归约”方法[54]。使用该方法时，首先确定方案或协议的安全目标；然后根据攻击者的能力构建一个安全模型；在构建安全模型中充分考虑攻击者的能力，并给攻击者提供所需要的一切资源，最后指出攻击者为了攻破协议的安全性，只有解决某个困难问题，即把攻击者攻破协议的能力归约到一个困难问题上。利用可证安全技术证明一个密码方案安全性的基本步骤是：

（1）安全性定义，即定义密码方案应能抵抗的攻击目标；

（2）形式化定义安全模型，即严格定义攻击者所掌握的攻击手段和资源；

（3）安全性证明，即将密码方案的安全性“归约”到一个已知的计算难题的过程。归约意味着针对某个密码方案的成功攻击者能够被转化为解决某个已知计算难题的有效算法，这个算法通过模拟攻击者攻击环境的方法来达到目的。由于相信针对某些计算难题的有效算法是不存在的，得到结论：不存在攻击者，能够以不可忽略的优势破解该密码方案。

到现在为止，电子现金协议的安全性证明可分为基于随机预言机模型和标准模型两种。随机预言机模型最早是由Bellare等人[52]于1993年提出，从Fiat等人[55]的思想中受到启发而从哈希函数抽象出来的一种通用证明模型。它要求将密码哈希函数看作真正的随机函数，即对应于不同的输入，它的输出是真正随机的。现有的大部分电子现金协议都是在随机预言机模型下证明其安全性的。利用随机预言机模型来证明协议的安全性的效率比较高，但是已经有一些协议虽然在随机预言机模型下被证明是安全的，但是在实际的方案中无法利用哈希函数来实例化，也就不能保证在实际情况下协议的安全性。标准模型无需随机预言机假设，直接把协议归约到一个困难问题上，直到2008年Groth和Sahai[37]提出第一个有效的非交互式零知识证明，利用此证明技术和P签名[56]，Belenkiy等人[25]构建了第一个标准模型下的电子现金协议。Izabachène等人[26]在标准模型下构建了第一个可分电子现金协议，但是其花费协议和存款协议的效率非常低。2015年Canard[29-30]和Baldimtsi等人[42]分别在标准模型下构建了可分电子现金协议和可传递电子现金协议。虽然基于标准模型的电子现金协议安全性比较强，但效率比较低。

5 电子现金协议现存的问题和研究展望

电子现金作为电子商务的重要支付手段，很多学者对其进行了研究，并从四个安全属性：条件性、可分性、可传递性和多银行性进行研究，为了保证所构建的协议是安全的，一般在随机预言机模型或者标准模型下进行证明。

综上所述，电子现金协议主要存在如下问题：

（1）现有的在标准模型下给出的电子现金协议，要么效率低下，要么不实用；

（2）现有的电子现金协议都是基于某个安全属性进行构建，为了方便使用，急需具有综合特性的电子现金协议；

（3）随着移动互联网的普及，越来越多的人使用智能手机来进行网络购物，而这都需要电子现金作为基础。但是，由于智能手机受电池和运行内存的限制，需要轻量级的电子现金协议作为基础。

因此，电子现金将来的研究重点如下：

（1）如何在标准模型下构建具有多种复合安全属性的高效电子现金协议

为了在标准模型下构建具有多种复合安全属性的电子现金协议，就需要一个有效的标准模型下的签名方案和零知识证明方案，然后基于有效的标准模型，借用签名和零知识证明，来构建有效的标准模型下的具有多种复合安全属性的电子现金协议。

（2）随着智能手机和移动支付的普及，如何构建具有各种安全属性的轻量级电子现金协议

轻量级电子现金协议是必经之路，为了能构建适合在智能手机上运行的电子现金协议，这就需要考虑新的可信模型，以便可以在普通智能手机上运行安全、可信赖的轻量级电子现金协议。

（3）区块链技术在电子现金领域的应用

区块链技术，特别是公开的无需许可的区块链能带来真正的电子现金。它被称为是人类信用进化史上继血亲信用、贵金属信用、央行纸币信用之后的第四个里程碑。区块链（blockchain）首次在Nakamoto发表的文章中[57]出现。区块链可分为三类[58]:

①区块链1.0是货币，它的应用都与货币有关，比如货币转移、汇兑和支付。

②区块链2.0是合约，顾名思义，区块链2.0就如同合约一样，不仅仅局限于现金的转移，它覆盖了经济、市场、金融全方面的应用，诸如债券、股票、贷款、期货、产权、智能合约和智能资产。

③区块链3.0的应用超越货币、金融、市场等领域，真正地实现全行业应用覆盖，例如政府、科学、文化、医疗和艺术等领域。

区块链具有如下特征：去中心化（decentralized）、去信任（trustless）、集体维护（collectively maintain）、可靠数据库（reliable database）。区块链是指通过去中心化和去信任的方式集体维护一个可靠数据库的技术方案。该技术方案让参与系统中的任意多个节点，把一段时间系统内全部信息交流的数据，通过密码学算法计算和记录到一个数据库block，并且生成该数据块的指纹用于连接chain下个数据库和校验，系统所有参与节点来共同认定记录是否为真。

2016年1月20日中国人民银行专门就数字货币召开了专题研讨会，指出：“发行数字货币既可以降低传统纸币发行、流通的高昂成本，又可以提升经济交易活动的便利性和透明度等作用。”区块链技术为比特币系统解决了数字加密货币领域长期以来所必须面对的两个重要问题，即双重支付问题和拜占庭将军问题。区块链作为未来新一代的底层基础技术，除了可以被应用到数字加密货币领域，还能延伸到金融、经济、科技和政治等其他领域。

6 结束语

本文首先概述了电子现金协议组成部分，并给出电子现金协议的一般模型，然后从四个安全特性出发，分析了不同安全特性的电子现金协议的国内外现状，并给出一些建设性的解决方法，再从随机预言机模型和标准模型出发，分析了当下电子现金协议的安全性证明进展。基于以上分析，给出了现有的电子现金协议存在的问题和最新的研究进展。

[1]Chaum D.Blind signatures for untraceable payments[C]//Proceedings of the Advances in Cryptology,Santa Barbara,USA,Aug 23-25,1982.New York:Springer Science Business Media,1983:199-203.

[2]Shi L,Carbunar B,Sion R.Conditional e-cash[C]//LNCS 4886:Proceedings of the 11th International Conference on Finan-cial Cryptography and Data Security,Scarborough,Trinidad and Tobago,Feb 12-16,2007.Berlin,Heidelberg:Springer,2007:15-28.

[3]Blanton M.Improved conditional e-payments[C]//LNCS 5037:Proceedings of the 6th International Conference on Applied Cryptography and Network Security,New York,Jun 3-6,2008.Berlin,Heidelberg:Springer,2008:188-206.

[4]Carbunar B,Tripunitara M.Conditional payments for computing markets[C]//LNCS 5339:Proceedings of the 7th International Conference on Cryptology and Network Security,Hong Kong,China,Dec 2-4,2008.Berlin,Heidelberg:Springer,2008:317-331.

[5]Li Ying,Chen Lusheng.Multi-conditional e-cash with transferability[C]//Proceedings of the 2010 International Conference on Wireless Communications,Networking and Information Security,Beijing,Jun 25-27,2010.Piscataway,USA:IEEE,2010:381-385.

[6]Carbunar B,Shi Weidong,Sion R.Conditional e-payments with transferability[J].Journal of Parallel and Distributed Computing,2011,71(1):16-26.

[7]Zhang Jiangxiao,Li Zhoujun,Guo Hua.Anonymous transferable conditional e-cash[C]//Proceedings of the 8th International ICST Conference on Security and Privacy in Communication Networks,Padua,Italy,Sep 3-5,2012.Berlin,Heidelberg:Springer,2013:45-60.

[8]Chen Xiaofeng,Li Jin,Ma Jianfeng,et al.New and efficient conditional e-payment systems with transferability[J].Future Generation Computer Systems,2014,37(7):252-258.

[9]Zhang Jiangxiao,Guo Hua,Li Zhoujun,et al.Transferable conditional e-cash with optimal anonymity in the standard model[J].IET Information Security,2014,9(1):59-72.

[10]Haddad G E,Hage H,Aïmeur E.E-payment plan:a conditional multi-payment scheme based on user personalization and plan agreement[C]//Proceedings of the 7th International Conference on E-Technologies:Embracing the Internet of Things,Ottawa,Canada,May 17-19,2017.Berlin,Heidelberg:Springer,2017:285-299.

[11]Okamoto T,Ohta K.Universal electronic cash[C]//LNCS 576:Proceedings of the 11th Annual International Cryptology Conference on Advances in Cryptology,Santa Barbara,USA,Aug 11-15,1991.Berlin,Heidelberg:Springer,1991:324-337.

[12]Eng T,Okamoto T.Single-term divisible electronic coins[C]//LNCS 950:Proceedings of the Workshop on the Theory and Application of Cryptographic Techniques,Perugia,Italy,May 9-12,1994.Berlin,Heidelberg:Springer,1994:306-319.

[13]Okamoto T.An efficient divisible electronic cash scheme[C]//LNCS 963:Proceedings of the 15th Annual International Cryptology Conference on Advances in Cryptology,Santa Barbara,USA,Aug 27-31,1995.Berlin,Heidelberg:Springer,1995:438-451.

[14]Chan A,Frankel Y,Tsiounis Y.Easy come-easy go divisible cash[C]//LNCS 1403:Proceedings of the 1998 International Conference on the Theory and Applications of Cryptographic Techniques,Espoo,Finland,May 31-Jun 4,1998.Berlin,Heidelberg:Springer,1998:561-575.

[15]Chen Kai,Zhang Yuqing,Xiao Guozhen.A divisible e-cash system based on probabilistic audit[J].Journal of Computer Research and Development,2000,37(6):752-757.

[16]Nakanishi T,Sugiyama Y.Unlinkable divisible electronic cash[C]//LNCS 1975:Proceedings of the 3rd International Workshop on Information Security,Wollongong,Australia,Dec 20-21,2000.Berlin,Heidelberg:Springer,2000:121-134.

[17]Camenisch J,Stadler M.Efficient group signature schemes for large groups[C]//LNCS 1296:Proceedings of the 17th Annual International Cryptology Conference on Advances in Cryptology,Santa Barbara,USA,Aug 17-21,1997.Berlin,Heidelberg:Springer,1997:410-424.

[18]Camenisch J,Hohenberger S,Lysyanskaya A.Compact ecash[C]//LNCS 3494:Proceedings of the 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques,Aarhus,Denmark,May 22-26,2005.Berlin,Heidelberg:Springer,2005:302-321.

[19]Peng Bing,Hong Fan,Cui Guohua.Divisible e-cash based on signatures of zero-knowledge proof and strong-RSA problem[J].Journal on Communications,2006,27(7):12-19.

[20]Canard S,Gouget A.Divisible e-cash systems can be truly anonymous[C]//LNCS 4515:Proceedings of the 26th Annual International Conference on the Theory and Applications of Cryptographic Techniques,Barcelona,Spain,May 20-24,2007.Berlin,Heidelberg:Springer,2007:482-497.

[21]Au M H,Susilo W,Mu Yi.Practical anonymous divisible ecash from bounded accumulators[C]//LNCS 5143:Proceedings of the 12th International Conference on Financial Cryp-tography and Data Security,Cozumel,Mexico,Jan 28-31,2008.Berlin,Heidelberg:Springer,2008:287-301.

[22]Chen Kai,Hu Yupu,Xiao Guozhen.Anonymity revocable divisible e-cash system[J].Journal of Xidian University:Natural Science,2001,28(1):57-61.

[23]Liu Wenyuan,Zhang Jiangxiao,Hu Qinghua,et al.Divisible e-cash system with direct computation and efficiency[J].Acta Electronica Sinica,2009,37(2):367-371.

[24]Canard S,Gouget A.Multiple denominations in e-cash with compact transaction data[C]//LNCS 6052:Proceedings of the 14th International Conference on Financial Cryptography and Data Security,Tenerife,Canary Islands,Jan 25-28,2010.Berlin,Heidelberg:Springer,2010:82-97.

[25]Belenkiy M,Chase M,Kohlweiss M,et al.Compact e-cash and simulatable VRFs revisited[C]//LNCS 5671:Proceedings of the 3rd International Conference on Pairing-Based Cryptography,Palo Alto,USA,Aug 12-14,2009.Berlin,Heidelberg:Springer,2009:114-131.

[26]Izabachène M,Libert B.Divisible e-cash in the standard model[C]//LNCS 7708:Proceedings of the 5th International Conference on Pairing-Based Cryptography,Cologne,Germany,May 16-18,2012.Berlin,Heidelberg:Springer,2012:314-332.

[27]Zhang Jiangxiao,Li Zhoujun,Guo Hua,et al.Efficient divisible e-cash in the standard model[C]//Proceedings of the 2013 IEEE International Conference on Green Computing and Communications and IEEE Internet of Things and IEEE Cyber,Physical and Social Computing,Beijing,Aug 20-23,2013.Piscataway,USA:IEEE,2013:2123-2128.

[28]Zhang Jiangxiao,Guo Hua,Li Zhoujun.Efficient divisible e-cash system based on reverse binary tree[J].Journal of Electronics&Information Technology,2014,36(1):22-26.

[29]Canard S,Pointcheval D,Sanders O,et al.Scalable divisible e-cash[C]//LNCS 9092:Proceedings of the 13th International Conference on Applied Cryptography and Network Security,New York,Jun 2-5,2015.Berlin,Heidelberg:Springer,2015:287-306.

[30]Canard S,Pointcheval D,Sanders O,et al.Divisible e-cash made practical[C]//LNCS 9020:Proceedings of the 18th IACR International Conference on Practice and Theory in Public-Key Cryptography,Gaithersburg,USA,Mar 30-Apr 1,2015.Berlin,Heidelberg:Springer,2015:77-100.

[31]Yang Bo,Yang Kang,Zhang Zhenfeng,et al.AEP-M:practical anonymous e-payment for mobile devices using ARM trustzone and divisible e-cash[C]//LNCS 9866:Proceedings of the 19th International Conference on Information Security,Honolulu,USA,Sep 3-6,2016.Berlin,Heidelberg:Springer,2016:130-146.

[32]Antwerpen H.Electronic cash[D].Eindhoven:Eindhoven University of Technology,1990.

[33]Okamoto T,Ohta K.Disposable zero-knowledge authentications and their applications to untraceable electronic cash[C]//LNCS 435:Proceedings of the 1989 Conference on the Theory and Applications of Cryptology,Advances in Cryptology,Santa Barbara,USA,Aug 20-24,1989.Berlin,Heidelberg:Springer,1990:481-496.

[34]Chaum D,Pedersen T.Transferred cash grows in size[C]//LNCS 658:Proceedings of the 11th Annual International Conference on the Theory and Applications of Cryptographic Techniques,Balatonfüred,Hungary,May 24-28,1992.Berlin,Heidelberg:Springer,1993:390-407.

[35]Canard S,Gouget A,Traoré J.Improvement of efficiency in(unconditional)anonymous transferable e-cash[C]//LNCS 5143:Proceedings of the 12th International Conference on Financial Cryptography and Data Security,Cozumel,Mexico,Jan 28-31,2008.Berlin,Heidelberg:Springer,2008:202-214.

[36]Canard S,Gouget A.Anonymity in transferable e-cash[C]//LNCS 5037:Proceedings of the 6th International Conference on Applied Cryptography and Network Security,New York,Jun 3-6,2008.Berlin,Heidelberg:Springer,2008:207-223.

[37]Groth J,Sahai A.Efficient non-interactive proof systems for bilinear groups[C]//LNCS 4965:Proceedings of the 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques,Istanbul,Turkey,Apr 13-17,2008.Berlin,Heidelberg:Springer,2008:415-432.

[38]Fuchsbauer G,Pointcheval D,Vergnaud D.Transferable constant-size fair e-cash[C]//LNCS 5888:Proceedings of the 8th International Conference on Cryptology and Network Security,Kanazawa,Japan,Dec 12-14,2009.Berlin,Heidelberg:Springer,2009:226-247.

[39]Blazy O,Canard S,Fuchsbauer G,et al.Achieving optimal anonymity in transferable e-cash with a judge[C]//LNCS 6737:Proceedings of the 4th International Conference on Cryptology in Africa,Dakar,Senegal,Jul 5-7,2011.Berlin,Heidelberg:Springer,2011:206-223.

[40]Zhang Jiangxiao,Li Zhoujun,Gao Yanwu,et al.Transferable e-cash system of equal length with optimal anonymity based on spending chain[J].Acta Electronica Sinica,2015,43(9):1805-1809.

[41]Zhang Jiangxiao,Huo Lina,Liu Xia,et al.Transferable optimalsize fair e-cash with optimal anonymity[C]//Proceedings of the International Symposium on Theoretical Aspects of Software Engineering,Nanjing,China,Sep 12-14,2015.Piscataway,USA:IEEE,2015:139-142.

[42]Baldimtsi F,Chase M,Fuchsbauer G,et al.Anonymous transferable e-cash[C]//LNCS 9020:Proceedings of the 18th IACR International Conference on Practice and Theory in Public-Key Cryptography,Gaithersburg,USA,Mar 30-Apri 1,2015.Berlin,Heidelberg:Springer,2015:101-124.

[43]Lysyanskaya A,Ramzan Z.Group blind digital signatures:a scalable solution to electronic cash[C]//LNCS 1465:Proceedings of the 2nd International Conference on Financial Cryptography,Anguilla,British West Indies,Feb 23-25,1998.Berlin,Heidelberg:Springer,1998:184-197.

[44]Jeong I R,Lee D H.Anonymity control in multi-bank ecash system[C]//LNCS 1977:Proceedings of the 1st International Conference on Cryptology in India,Progress in Cryptology,Calcutta,India,Dec 10-13,2000.Berlin,Heidelberg:Springer,2000:104-116.

[45]Wang Shangping,Chen Zhiqiang,Wang Xiaofeng.A new certificateless electronic cash scheme with multiple banks based on group signatures[C]//Proceedings of the International Symposium on Electronic Commerce and Security,Guangzhou,China,Aug 3-5,2008.Piscataway,USA:IEEE,2008:362-366.

[46]Chen Mingte,Fan C I,Juang W S,et al.An efficient electronic cash scheme with multiple banks using group signature[J].International Journal of Innovative Computing,Information and Control,2012,8(7):4469-4482.

[47]Zhang Jiangxiao,Li Zhoujun,Guo Hua.Multiple-bank ecash without random oracles[C]//LNCS 8300:Proceedings of the 5th International Symposium on Cyberspace Safety and Security,Zhangjiajie,China,Nov 13-15,2013.Berlin,Heidelberg:Springer,2013:40-51.

[48]Goldwasser S,Micali S,Rackoff C.The knowledge complexity of interactive proof-systems[C]//Proceedings of the 17th Annual ACM Symposium on Theory of Computing,Providence,USA,May 6-8,1985.New York:ACM,1985:291-304.

[49]Chaum D.Blind signatures for untraceable payments[C]//Proceedings of the Crypto 82,Advances in Cryptology,Santa Barbara,USA,Aug 23-25,1982.Berlin,Heidelberg:Springer,1982:199-203.

[50]Abe M,Fuchsbauer G,Groth J,et al.Structure-preserving signatures and commitments to group elements[C]//LNCS 6223:Proceedings of the 30th Annual Cryptology Conference on Advances in Cryptology,Santa Barbara,USA,Aug 15-19,2010.Berlin,Heidelberg:Springer,2010:209-236.

[51]Yao A C.Protocols for secure computations[C]//Proceedings of the 23rd Annual Symposium on Foundations of Computer Science,Chicago,USA,Nov 3-5,1982.Washington:IEEE Computer Society,1982:160-164.

[52]Bellare M,Rogaway P.Random oracles are practical:a paradigm for designing efficient protocols random oracles are practical:a paradigm for designing efficient protocols[C]//Proceedings of the 1st ACM Conference on Computer and Communications Security,Fairfax,USA,Nov 3-5,1993.New York:ACM,1993:62-73.

[53]Goldwasser S,Micali S.Probabilistic encryption[J].Journal of Computer and System Sciences,1984,28(2):270-299.

[54]Feng Dengguo.Research on theory and approach of provable security[J].Journal of Software,2005,16(10):1743-1756.

[55]Fiat A,Shamir A.How to prove yourself:practical solutions to identification and signature problems[C]//LNCS 263:Proceedings of the 1986 Conference on the Theory and Applications of Cryptographic Techniques,Advances in Cryptology,Santa Barbara,USA,Aug 11-15,1986.Berlin,Heidelberg:Springer,1987:186-194.

[56]Belenkiy M,Chase M,Kohlweiss M,et al.P-signatures and noninteractive anonymous credentials[C]//LNCS 4948:Proceedings of the 5th Theory of Cryptography,New York,Mar 19-21,2008.Berlin,Heidelberg:Springer,2008:356-374.

[57]Nakamoto S.Bitcoin:a peer-to-peer electronic cash system[EB/OL].(2009).https://bitcoin.org.bitcoin.pdf.

[58]Swan M.Blockchain:blueprint for a new economy[M].Sebastopol,USA:O'Reilly Media Press,2005.

附中文参考文献：

[15]陈恺,张玉清,肖国镇.基于概率验证的可分电子现金系统[J].计算机研究与发展,2000,37(6):752-757.

[19]彭冰,洪帆,崔国华.基于零知识证明签名和强RSA问题的可分电子现金[J].通信学报,2006,27(7):12-19.

[22]陈恺,胡予濮,肖国镇.可撤消匿名性的可分电子现金系统[J].西安电子科技大学学报:自然科学版,2001,28(1):57-61.

[23]刘文远,张江霄,胡庆华,等.可直接计算的高效的可分电子现金系统[J].电子学报,2009,37(2):367-371.

[28]张江霄,郭华,李舟军.基于逆序二叉树的高效可分电子现金系统[J].电子与信息学报,2014,36(1):22-26.

[40]张江霄,李舟军,高延武,等.基于花费链最优匿名的等长可传递电子现金系统[J].电子学报,2015,43(9):1805-1809.

[54]冯登国.可证明安全性理论与方法研究[J].软件学报,2005,16(10):1743-1756.

2017-06,Accepted 2017-09.

Survey on E-Cash Scheme*

LI Zhoujun1,ZHANG Jiangxiao2+,FENG Chunhui2,SUI Chunrong2
1.State Key Laboratory of Software Development Environment,Beihang University,Beijing 100191,China
2.Mathematics and Information Technology Institute,Xingtai University,Xingtai,Hebei 054001,China
+Corresponding author:E-mail:orange_0092008@163.com

With the rapid development of the network,the scale of e-commerce is getting bigger and bigger.Electronic cash(e-cash)is an important payment method to e-commerce and attracts a lot of scholars at home and abroad to study it and design a conditional,divisible,transferable or multi-bank e-cash protocol.How to design a safe e-cash protocol with various characteristics is a very important research topic.This paper firstly introduces the basic model of the e-cash protocol.Secondly,this paper introduces the definition,development status and existing problems of the e-cash protocol from various characteristics and gives the application of the e-cash protocol.Thirdly,the important cryptographic primitives are given to construct the e-cash protocol and the provable security theory is described to prove the security of the e-cash protocol.Finally,the problems of the e-cash protocol are summarized and the latest research direction is given.

e-commerce;e-cash scheme;standard model;zero-knowledge proofs;anonymity;blockchain

10.3778/j.issn.1673-9418.1706050

*The Social Science Foundation of Hebei Province under Grant No.HB16TQ016(河北省社会科学基金项目).

CNKI网络优先出版:2017-09-05,http://kns.cnki.net/kcms/detail/11.5602.TP.20170905.1205.008.html

LI Zhoujun,ZHANG Jiangxiao,FENG Chunhui,et al.Survey on e-cash scheme.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1701-1712.

A

TP309

LI Zhoujun was born in 1963.He received the Ph.D.degree in computer from National University of Defense Technology in 1999.Now he is a professor and Ph.D.supervisor at Beihang University,and the senior member of CCF.His research interests include network and information security,etc.

李舟军（1963—），男，湖南湘潭人，1999年于国防科技大学获得计算机博士学位，现为北京航空航天大学教授、博士生导师，CCF高级会员，主要研究领域为网络与信息安全。

ZHANG Jiangxiao was born in 1983.He received the Ph.D.degree in network information security from Beihang University in 2014.Now he is a lecturer at Xingtai University,and the member of CCF.His research interests include e-commerce,e-cash and block-chain,etc.

张江霄（1983—），男，河北邢台人，2014年于北京航空航天大学获得网络信息安全博士学位，现为邢台学院数学与信息技术学院讲师，CCF会员，主要研究领域为电子商务，电子现金，区块链等。

FENG Chunhui was born in 1964.She is a professor at Xingtai University.Her research interest is database technology.冯春辉（1964—），女，河北隆尧人，邢台学院数学与信息技术学院教授，主要研究领域为数据库技术。

SUI Chunrong was born in 1969.She received the M.S.degree from Hebei University in 1993.Now she is an associate professor at Xingtai University.Her research interest is computer network.

隋春荣（1969—），女，黑龙江虎林人，1993年于河北大学获得硕士学位，现为邢台学院数学与信息技术学院副教授，主要研究领域为计算机网络。