双约束条件下PMVS的改进算法

杨文博，孙博文

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

双约束条件下PMVS的改进算法

杨文博，孙博文+

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

PMVS（patch-based multi-view stereo）算法以其良好的表现，在多视立体领域得到广泛应用。然而，算法存在重建模型细节丢失与重建点位置不够精确的问题，这种情况在输入图片较少，重建场景纹理不明显时尤为严重。针对这些不足，对去除候选误匹配点及对种子点置信度的排序进行了研究：引入USAC（Universal-RANSAC）去除候选误匹配点方法；提出双约束条件策略，筛选出候选空间点中置信度较高的点作为种子点。重建模型细节与原物体的契合度有了很大提高，纹理较少模型的重建点云数明显增加，漏洞也明显减少。通过在真实数据集上的实验，验证了改进算法具有更强的有效性和实用性。

PMVS算法；Universal-RANSAC；双约束条件；多视立体重建

1 引言

作为计算机视觉的研究热门，三维重建技术不管是从理论方面还是从实践方面都日臻成熟。理论上，SFM（structure from motion）技术[1-2]中Bundler算法[3]的提出及完善[4]进一步促进了三维重建技术的发展。实践中，三维重建技术在诸如医疗、测量、文化遗产保护、3D电影娱乐、军事以及虚拟现实等领域的广泛应用，使得更多的研发人员加入到开发使用三维重建技术[5]的行列。传统的三维重建技术由于其自动化程度较低，并且开发周期较长，设备昂贵及只适用于室内场景等缺陷，应用受到了很大限制。多视立体重建技术则克服了以上缺点，得到了广泛研究[6-7]。

把输出场景再现作为基准来对多视立体算法进行分类，目前最为流行的多视立体算法分为如下4类：

（1）基于点云的方法[8-9]；

（2）基于深度图的方法[10-11]；

（3）基于体积标量场的方法[12-13]；

（4）基于网格的方法[14-15]。

在上述4类方法中，后3种方法都需要一些初始信息，如对视差范围、表面进行初始化等。这一要求极大地限制了它们在重建复杂大场景中的应用，而是仅仅适用于重建单个物体，因为在复杂大场景情况下，几乎是无法正确估计所需的初始信息的。与这3种方法有所差异，前者不会用到任何初始化信息。该方法是由Furukawa等人提出的PMVS（patchbased multi-view stereo）算法，不管是在重建精度还是在重建完整性上都具有非常好的表现，该算法是这类算法的代表，同时也代表了当前多视重建所达到的水平。该算法在很多场景重建特别是室外大场景重建中都有很好的重建效果[16-17]。尽管这样，在实际的应用中，会发现该算法仍然有需要改进的地方。本文针对原始PMVS算法的不足提出了一些改进方法。

2 PMVS算法及其改进

PMVS算法是一种对物体从多个角度拍摄所形成的多张图像进行匹配，然后依据一定几何约束条件重建三维点云的算法。其核心思想可以理解为以下几步：首先将每幅图像中的特征点用Harris+DoG算子提取出来，并对特征点对进行匹配，在满足极线几何约束的条件下，采用三角化方法生成以三维空间点为中心的矩形面片，该面片被称为以法向量为具体方向的种子面片；然后以相邻点云片的两个相似特性为条件（法向量和空间点位置），一步步将种子点云片的邻近相似点云片扩散并重建出来；最后，扩散结束后需要进行过滤处理操作，将不满足一致性的错误面片剔除。其中PMVS在扩散和过滤阶段需要迭代运行n次，n一般取值为3。通过这种方式，算法可以鲁棒性地扩散出稠密的三维空间面片。

2.1 基本定义

按照文献[7]，基本定义如下：

定义1（面片模型）面片（又称点云片）p是一个小平面矩形，该平面与所重建物体表面近似相切。每个面片p对应一个参考图像R(p)，R(p)对p保持可见。

c(p)为面片p的中心；n(p)为面片p的单位法线；R(p)为面片p的参考图像；V(p)为面片p的准可见图像集（所有包含面片p的图像集合，图像集中包含那些面片p应该被看到但是由于运动模糊、遮挡、高光等而不被看到的图像）；V*(p)为图像集中面片p都能被看到的图像集。其中：

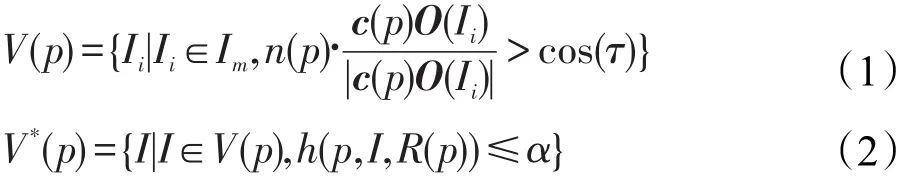
式（1）中O(Ii)为参考图像光心，不等式左边表示面片p的单位法向量与经过p中心与O(Ii)形成向量的单位向量的点积，τ=π/3。

定义2（图像模型）将图像集合Ii中的每一幅图像都划分成大小为β×β像素的图像小块Ci(x,y（)实验中β取值为2）。这里x、y是图像块的下标，i表示的是第i张图像。Qi(x,y)是用于记录投射到V(p)中每个图像块Ci(x,y)的所有点云片的集合。

C(p)为点云片p在V(p)中的毗邻块形成的集合。

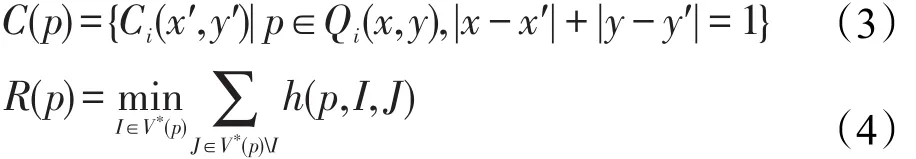
定义3（灰度一致性函数）对于一个点云片p，在其集合V*(p)上的灰度一致性函数g*(p)被定义为：

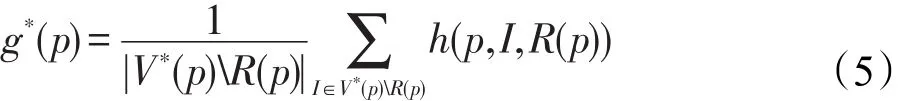
式（5）中，h(p,I,R(p))为R(p)和图像I之间的灰度一致性度量函数。

2.2 重建流程

（1）特征点的提取、匹配以及种子面片的生成。首先使用Harris和DoG算子对图像集合中的全部相关特征点进行提取，对于每一幅图像Ii中的每一个特征点，在图像集的其余图像中分别找到该特征点与R(p)光心O(Ii)所形成直线在每幅图像中的投射直线，专业上称这条线为极线。将极线周围两个像素误差内的所有特征点作为该特征点的潜在匹配点进行匹配，从而形成该特征点的匹配点对，然后再采用三角化方法将这些匹配点对形成三维空间点，最后根据这些三维空间点到该特征点所对应的参考图像光心O(Ii)的距离从小到大进行排序，依照这样的顺序，对该距离所对应的三维空间点依次尝试生成面片p，直到生成面片成功为止。其中面片的中心c(p)为能够成功生成面片的三维空间点，而该有向面片的单位法向量n(p)为c(p)指向参考图像光心O(Ii)的单位法向量。通过式（1）、（2）来确定面片的准可视图像集V(p)和可视图像集V*(p)。然后对c(p)和n(p)进行优化，优化过程是通过最小化式（5）来完成的。优化完成后再次利用式（1）、（2）对V(p)和V*(p)进行更新，其中τ的值保持不变，由于优化前后面片的灰度一致性度量值会显著提高，从而α的值变为0.3。最后，如果优化后的可视图像集V*(p)满足大于等于γ（取值为3）的条件，则表示重建成功，此时将所创建的面片p存储到V(p)和V*(p)对应的图像块中，同时对集合Qi(x,y)和进行更新。

（2）对初始种子面片进行扩散。对点云片进行扩散这一环节是以尽量使得Ci(x,y)中的点云数不小于1为目标的。首先使用式（3）确定面片p所对应的邻域图像块集C(p)，从该图像块集合中选出满足一定约束条件的图像块Ci(x′,y′)，对其尝试扩散出一个新的面片p′，这里将面片p所在平面与穿过Ci(x,y)中心的可视光线所形成的交点作为面片p′的初始中心值，即c(p′)。将面片p的n(p)、V(p)、R(p)作为p′的初始值分别赋值给n(p′)、V(p′)、R(p′)，用式（2）对可视图像集V*(p)进行初始化。然后再对c(p′)和n(p′)进行优化，优化之后，根据深度测试条件来判断面片p′对应的准可视图像，将准可视图像加入到V(p′)中，并利用式（3）再次对V*(p′)进行更新。最后，如果V*(p′)满足条件V*(p′)≥γ，则新扩散出的面片是可接受的。

（3）过滤。整个过滤过程是通过3个过滤器来实现的，前两个过滤器是利用可视一致性约束条件来剔除重建表面的内点和外点。而第三个过滤器则是通过强加一个较弱的规则实现的。整个算法流程如图1所示。

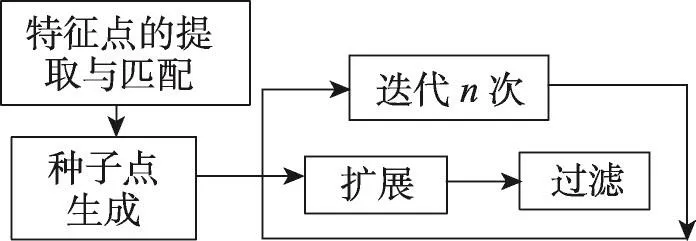
Fig.1 Flowchart of PMVS algorithm图1PMVS算法流程

2.3 存在问题

PMVS算法存在以下问题：

（1）在重建种子面片的过程时，该算法存在相对较大的匹配误差及选取候选三维空间点误差，而误差的累积使得重建出点云空间位置不够精确，累积达到一定程度，甚至会出现错误点。这样，在稠密匹配阶段，如果得到的种子点不够准确，就会产生大量不准确的重建点。这对于输入图像较少，提取特征点不多的情况，以及所重建物体表面纹理较少的情况来说，其影响是巨大且不可忽略的。因此，减少重建过程中的各种误差，谨防误差过度积累，是重建结果进行优化的一个重要方面。

（2）原算法通过匹配点生成三维空间点后，会将这些点按照距离从小到大进行排序，然后依次尝试生成面片，直到成功，该方法存在一定的盲目性。

2.4 PMVS算法的改进

本文改进后的算法流程如图2所示。

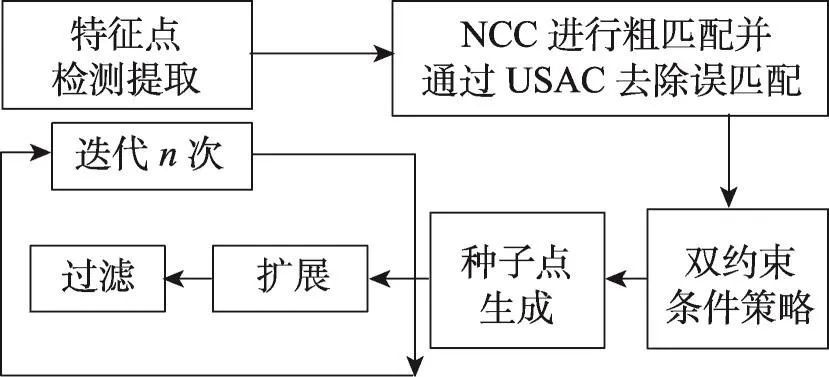
Fig.2 Flowchart of the proposed algorithm图2 本文算法运行流程图

对于第一个问题，本文在特征点检测后使用NCC（normalized cross correlation）算法[18]对其进行粗匹配，之后，误匹配的消除是通过使用Universal-RANSAC[19]（该算法解决了经典RANSAC算法在效率、精度、退化三方面上的局限性，几乎所有比较前沿的RANSAC改进算法都是它的一个特例，简称USAC）来实现的，从而一些鲁棒性较差的点被消除，有效地减少扩散阶段误匹配的累积，同时该阶段运行的时间也有减少，区域的搜索范围也有缩小，整个系统的计算速度也有所增加。而减少候选三维空间点的误差，在问题（2）的解决方案中得到了很好的解答。

对于问题（2），本文提出双约束条件来对三维空间点进行选取，从而提高创建种子点的运行速度及所创建种子点的置信度。其中，双约束条件即去最值取平均策略和点的置信度策略。

（1）去最值求平均策略

用匹配点对使用三角化方法生成一系列三维空间点，然后将这些点按照距离O(Ii)从小到大进行排序，假设有n个这样的三维点。首先根据n值的大小来设定一个合适的阈值，该阈值的作用有两个，判断是否对最值点进行去除以及去除两端最值的百分比，从而解决了问题（1）中所说的减少选取候选三维空间点误差问题，然后求得剩余距离总和的均值d。优先选取距离均值d最近的距离，并以其对应的三维空间点为中心，开始尝试重建面片。

本策略依据的是正态分布原理。为了验证此依据的正确性，本文将由匹配点对集合（极线几何一致性约束条件）生成的一系列三维空间点作为输入数据，分别对这些点在x、y、z坐标轴上进行正态分布测试，其测试结果如图3（a）所示。根据直方图所绘制的曲线看起来很像正态分布曲线，其中高概率点基本都位于曲线对称轴左右。为了进一步证明这些点数据符合正态分布，本文通过正态Q-Q图进行检验。如图3（b）所示，可以看出各点近似围绕着直线，说明数据呈近似正态分布。

（2）点的置信度策略

利用上述算法对待匹配特征点和候选匹配点进行匹配时，每一对匹配点对都会得到相应的相似度匹配分数，创建种子云面片时，选择满足一定条件的最高分，这里将该匹配点对所获得的三维空间点附加一个阈值限制条件。本文定义该限制条件为，当前云面片距离不小于双约束条件（1）中所计算平均距离时，其云面片距离与平均距离之比小于等于1.3（阈值）；当前云面片距离不大于双约束条件（1）中所计算平均距离时，云面片距离与平均距离之比大于等于0.7（阈值）；从而提高点的置信度。

综合本文提出的两种策略作为约束条件，实现对三维空间点的选取。

2.5 原算法以及改进算法参数寻优策略

通过2.3节可知，原PMVS算法依次尝试生成面片的过程具有一定的盲目性。假设能够成功生成的空间点位于距离比较大的位置，那么比该距离小的所有空间点都得依次尝试生成面片，并都会以失败告终，这些操作是耗时并且没有必要的。即使距离光心距离较小的点能够成功创建面片，也不一定是在最优的三维空间点位置创建的。再者，如果生成的面片点恰好是误匹配点或者置信度不太高的匹配点生成的，就会产生错误的种子点或者置信度不高的种子点。这一点不处理好的话，扩散阶段，误差的累积就会产生错误的或不准确的面片，使得重建模型细节不能够很好地重建出来，增加了区域增长的运行时间，同时也占用了不少的内存资源。

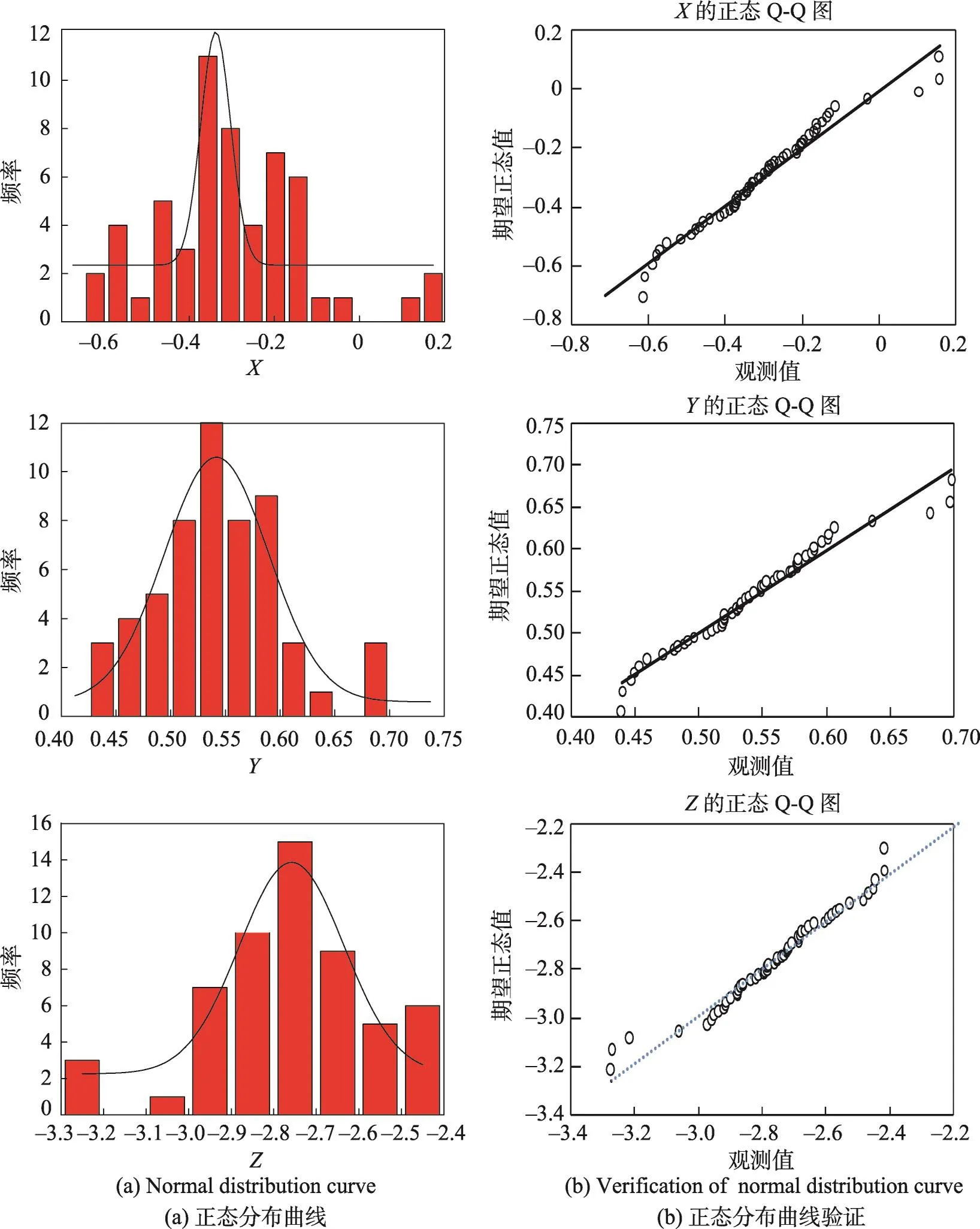
Fig.3 Detection of normal distribution图3 正态分布检测

通过2.4节可知，改进算法在通过匹配点生成三维空间点后，同样会将这些点按照距离从小到大进行排序，但并非像原算法那样从小到大依次尝试生成面片，而是通过本文提出的双约束条件策略对这些有序点进行选取，选取那些能够成功生成面片概率较大并且置信度较高的点，将平均值点及其左右周围点依次插入数组中，然后从数组中选取点尝试生成面片，直到成功。

2.6 原算法以及改进算法时间复杂度分析

本文是对初始面片的生成阶段进行研究，该阶段原算法伪代码详细步骤归纳如下。

本文在选取特征点集合F时利用USAC算法去除误匹配点，并使用双约束条件将集合F中置信度较高的点插入到集合F的前端，然后进入算法第三步。改进算法伪代码如下。

其中，算法步骤2.3为根据创建点时的分数以及该点的距离两条件设置阈值，将不符合条件点进行剔除，进一步提高点置信度。算法步骤3之后操作与原算法相同，这里省略。

算法时间复杂度分析：假设总共有m张图片，每张图片被分为p×q大小的网格，并假设网格中只有一个特征点，而利用极线几何约束条件找到该特征点在其他图像中的匹配点数总和为n,即集合F中点的个数，这里n为原算法步骤3的规模。设步骤3中代码的实际运行次数是s。为了方便计算，这里忽略原算法步骤3中的删除p对应图像块中的所有特征点这一操作，则原算法的时间复杂度为O(m×p×q×s)。由于原算法选取点的盲目性，使得s的值趋近于n/2。即实际时间复杂度为O(m×p×q×n/2)，本文通过对置信度较高的点进行选取，从而使得s的范围基本在1～3之间，由此本文在该阶段时间复杂度为O(m×p×q)。可以看出，当n的规模不大时，本文算法与原算法在时间上基本无差别，但重建精度及重建面片数却有很大提高；当n的规模较大时，本文算法在时间以及重建结果上就可以很好地表现出来，这一点在本文实验中的Buddha数据集上得到了验证。

此外，由于本文改进算法在初始面片选取阶段选取了置信度较高的种子点，而扩散阶段，面片是以这些种子点为基准进行扩散的，从而使得扩散出的点置信度也较高。迭代该过程3次使得最终面片的精度以及重建面片的数量都得到了提高。

3 实验

本文利用提出的改进算法与其PMVS原算法进行三维重建结果的对比，并用7组数据对其进行分析和验证。这里所采用的数据都是公共数据集，实验环境为Intel®CoreTMi7-4790K，8 GB内存，处理器主频为4.0 GHz，在Windows7 64操作系统下，利用VS2010对所有算法进行了实现。

文中使用 PER（patch enhancement rate）和 ERR（error reduction rate）来分别表示面片提高率及面片错误降低率，并使用NORP（number of reconstructed patches）、NOPAR（number of patches after remove）及ROP（rate of patch）来分别代替重建面片数、去杂点后面片数、面片错误率。文中对面片提高率、错误降低率以及面片错误率的定义如下：设改进算法去除杂点后面片数、原算法去除杂点后面片数、原算法面片错误率、改进算法面片错误率分别为M、N、X、Y。

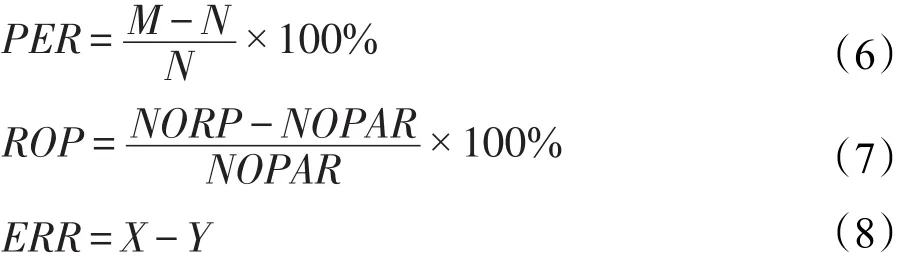
本文的实验数据集包括Kermit、ET、Dino、Temple、Buddha、清华生命科学楼（下文使用QHB来代替）、教堂。算法对各个数据集的重建效果如图4～图10所示，实验中所涉及的各参数与原算法保持一致，数据集中所有图像用Bundler获得摄像机参数。

如图4（a）所示，Kermit[20]模型纹理比较清晰，输入11张图片就能很好地完成模型的创建。PMVS算法和改进算法重建的效果都比较好，但是PMVS算法在头部和身体等某些细节部分的体现并不是很理想，如图4（b）红色椭圆标记区域。从整体模型的重建完整度得知，本文改进算法漏洞很少，头部、身体等部位的重建完整性更好，如图4（c）红色椭圆标记区域。原算法重建点云面片数为9 944，本文算法则为12 624。

如图5（a）所示，该Dino模型比较光滑，纹理相对较少，每幅图片获得的特征点较少，需要输入几十张照片才能创建出效果较好的模型，如图5（b）所示。PMVS算法对该数据集的重建效果并不是很理想，很多细节部位都存在较大漏洞，算法创建的面片数也只有8 370，时间为11 s。相比之下，如图5（c）所示，改进后的模型效果则好很多，重建的面片数为11 267，时间也减少为8 s。

图5～图7是文献[21-22]中的Dino、Temple以及ET。从数据集在PMVS算法和本文改进算法的基础上的应用结果得知，本文算法相对于PMVS原算法来说都有很大的提高。

Fig.4 Results of reconstructed Kermit by PMVS and improved algorithm图4 PMVS和改进后PMVS重建Kermit的结果

Fig.5 Results of reconstructed Dino by PMVS and improved algorithm图5 PMVS和改进后PMVS重建Dino的结果

图8是Autodesk 123D Catch中的实例图片，图9的数据集来源于中国科学院自动化研究所模式识别国家重点实验室（http://vision.ia.ac.cn/data），图10的数据集来源于网站下载（http://www.robots.ox.ac.uk/～vgg/data/data-mview.html）。原算法和本文改进算法都对模型有了很好的重建，但PMVS算法对某些细节有些丢失，如图8（b）、图9（b）、图10（b）所示。改进后的重建效果则弥补了这一不足，如图8（c）、图9（c）、图10（c）所示。图8中PMVS算法重建点云数（面片数）为278 209，本文改进算法则为288 986。生成面片的提高率达到8.04%，生成面片错误降低率更是达到了4.21%，重建的时间也从原算法的328 s变为现在的284 s。图9中原算法重建点云面片数为70 707，本文算法则为76 558。面片的提高率为8.275%，生成面片的错误降低率为2.663%。图10中PMVS算法重建点云面片数为7 042，本文改进算法则为9 081，面片的提高率为28.950%，生成面片的错误降低率为4.562%。两算法相较而言，本文算法生成面片的提高率及错误的降低率都有了很大的提升。

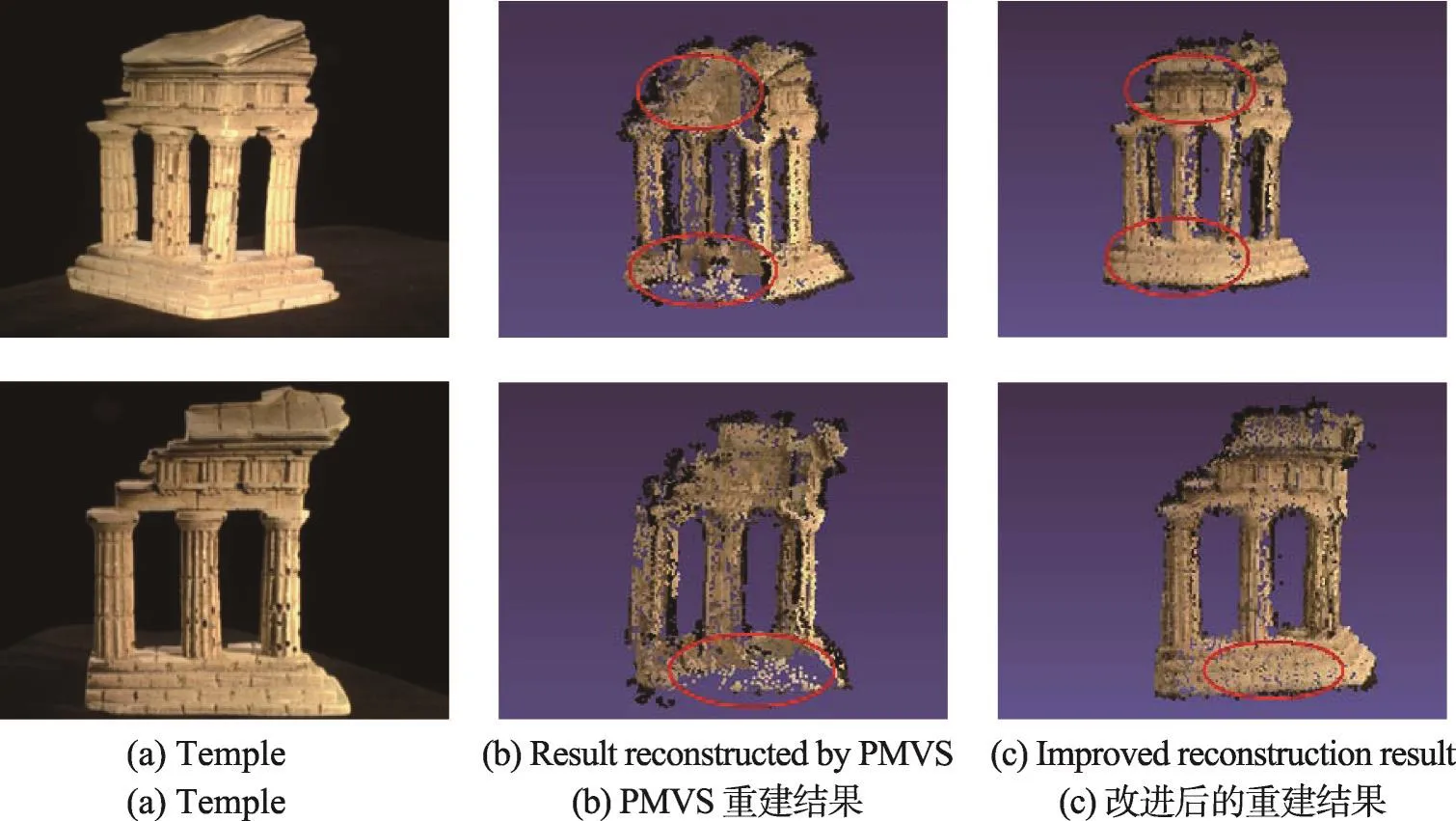
Fig.6 Results of reconstructed Temple by PMVS and improved algorithm图6 PMVS和改进后PMVS重建Temple的结果

Fig.7 Results of reconstructed ET by PMVS and improved algorithm图7 PMVS和改进后PMVS重建ET的结果

Fig.8 Results of reconstructed Buddha by PMVS and improved algorithm图8 PMVS和改进后PMVS重建Buddha的结果

表1为PMVS算法与本文算法在给定实验数据集上得到的面片数以及运行时间的对比。从表中可以看出，除了第四组数据，本文算法在其他数据集上得到的点云数据相比于PMVS算法都有很大提高，这种提高在输入图片较少并且图像纹理较弱的数据集上表现尤为明显。在运行时间基本相同，甚至减少的情况下，Kermit、Dino、Church重建面片数分别从原算法的9 944、8 370、7 042变为本文算法的12 624、11 267、9 081，面片数增加幅度显著。针对于第四组数据，本文在下面会给予解释。这里，表中的面片数是去除杂点后的面片数。

Fig.9 Results of reconstructed Tsinghua by PMVS and improved algorithm图9 PMVS和改进后PMVS重建清华生命科学楼的结果

Fig.10 Results of reconstructed church by PMVS and improved algorithm图10 PMVS和改进后PMVS重建教堂的结果

Table 1 Comparison of PMVS and improved algorithm for reconstruction of facet number and running time表1 原算法与改进算法重建面片数及时间对比分析结果

表2、表3为各个实验数据集合上，PMVS算法和本文算法产生的面片错误率。表中第三行是所计算的面片错误率。从表中得知PMVS原算法的重建面片错误率都高于本文算法。其中，Kermit、Buddha、Church重建面片的错误率分别从4.595%、12.258%、8.020%降低为0.001%、8.041%、3.460%，降低幅度显著，特别是在输入图像较少，模型表面纹理少的Dino数据集上，错误率从12.438%降为5.533%。

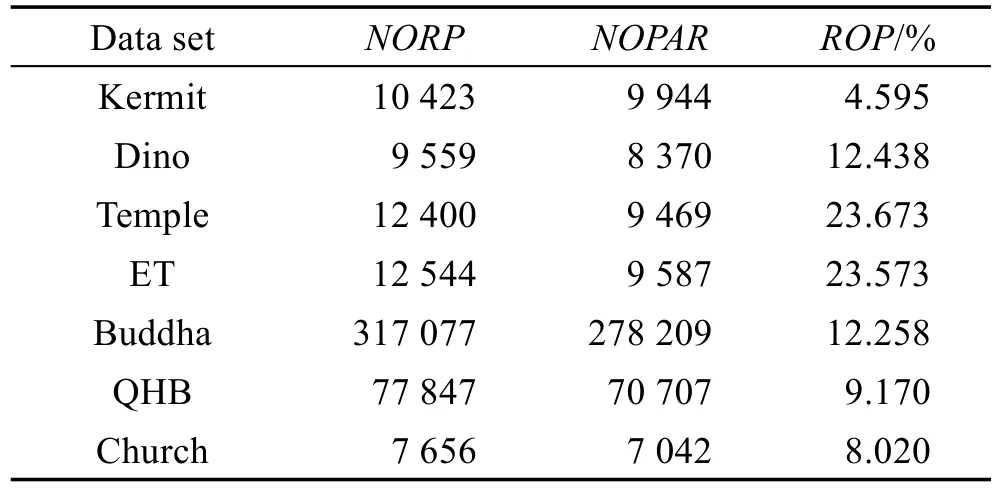
Table 2 PMVS algorithm for reconstructing error rate of point cloud表2 PMVS算法重建点云错误率

Table 3 Improved algorithm for reconstructing error rate of point cloud表3 改进算法重建点云错误率

表4为本文算法与PMVS算法在实验数据集合上，对面片提高率、错误降低率进行的比较结果。从表中可以得知，各组数据面片的提高率以及面片的错误降低率都有了很大的提高。最为显著的莫过于纹理较少的Dino数据集，面片提高率高达34.612%，错误降低率也高达6.905%，很好地解决了原算法在图像纹理较少时，面片重建精度不高的问题。表1中数据之所以会不同，是因为输入图片数量较少，重建正确面片数相差不多且数据量不大的情况下，正确率就显得极为重要，这一点可以从图7重建的结果对比中清晰地表达出来。

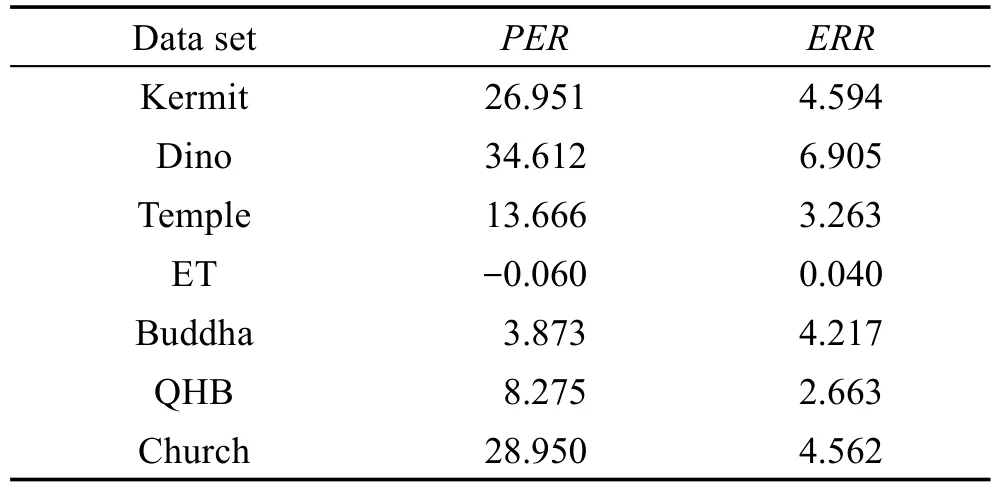
Table 4 Patch enhancement rate and error reduction rate of improved algorithm表4 改进算法的面片提高率及面片错误降低率 %

国内对PMVS算法的研究有很多，但大多都是从特征点的检测与提取阶段入手，使用其他特征匹配算法来代替该阶段的匹配算法，还有一些从扩散阶段面片的方向优化入手等，其结果也是差强人意。史颖等人[6]与本文一样也是对种子点置信度的排序进行研究，提出了MFPMVS（patch with multiple features based multi-view stereopsis）算法，并且取得了很好的重建效果。这里，将本文改进算法与之进行对比，其结果如表5所示。表中的面片数与表1中的数据不同，是因为这里需要与MFPMVS算法保持同步，即使用的是去除杂点前的数据。从表中可知本文算法与MFPMVS算法重建面片数基本相同，而MFPMVS算法是在牺牲时间效率的前提下进行的，但本文改进算法在达到重建结果基本相同的条件下，同时也降低了时间复杂度。

Table 5 Comparison of improved algorithm and MFPMVS for reconstruction of facet number表5 本文改进算法与MFPMVS算法重建面片数对比分析结果

4 结束语

本文在PMVS算法的基础上，针对其细节重建效果不佳，创建稠密点云错误点较多，对纹理不太明显物体重建效果极差等缺点进行了改进。所测数据，生成稠密点云中点云的错误降低率提高了0.040%～6.905%，使得点云扩建细节问题得到了很好的解决。点云的面片提高率为3.873%～34.612%，使得纹理不太明显物体重建出点云片较少问题得到了很好的解决。可以得知，本文算法具有更强的稳定性和实用性。

[1]Wu Changchang.Towards linear-time incremental structure from motion[C]//Proceedings of the 2013 International Conference on 3D Vision,Seattle,Washington,USA,Jun 29-Jul 1,2013.Washington:IEEE Computer Society,2013:127-134.

[2]Zheng E,Wu Changchang.Structure from motion using structure-less resection[C]//Proceedings of the 2015 International Conference on Computer Vision,Santiago,Chile,Dec 7-13,2015.Washington:IEEE Computer Society,2015:2075-2083.

[3]Triggs B,McLauchlan P F,Hartley R I,et al.Bundle adjustment—a modern synthesis[C]//LNCS 1883:Proceedings of the 1999 International Workshop on Vision Algorithms:Theory and Practice,Corfu,Greece,Sep 21-22,1999.Berlin,Heidelberg:Springer,1999:298-372.

[4]Wu Changchang,Agarwal S,Curless B,et al.Multicore bundle adjustment[C]//Proceedings of the 24th Conference on Computer Vision and Pattern Recognition,Colorado Springs,USA,Jun 20-25,2011.Washington:IEEE Computer Society,2011:3057-3064.

[5]Vazquez-Duchêne M D,Freis O,Denis A,et al.Virtual reality for skin exploration[C]//Proceedings of the 2013 Virtual Reality International Conference,Laval,France,Mar 20-23,2013.New York:ACM,2013:5.

[6]Shi Ying,Wang Wenjian,Bai Xuefei.3D dense reconstruction method based on multiple features[J].Journal of Frontiers of Computer Science and Technology,2015,9(5):594-603.

[7]Shi Limin,Guo Fusheng,Hu Zhanyi.An improved PMVS through scene geometric information[J].Acta Automatica Sinica,2011,37(5):560-568.

[8]Furukawa Y,Curless B,Seitz S M,et al.Towards internetscale multi-view stereo[C]//Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition,San Francisco,USA,Jun 13-18,2010.Washington:IEEE Computer Society,2010:1434-1441.

[9]Furukawa Y,Ponce J.Accurate,dense,and robust multiview stereopsis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(8):1362-1376.

[10]Taveira G,Fernandes L A F.Automatic alignment and reconstruction of facial depth images[J].Pattern Recognition Letters,2014,50(C):82-90.

[11]Matyunin S,Vatolin D,Berdnikov Y,et al.Temporal filtering for depth maps generated by kinect depth camera[C]//Proceedings of the 3DTV Conference:The True Vision-Capture,Transmission and Display of 3D Video,Antalya,Turkey,May 16-18,2011.Piscataway,USA:IEEE,2011:1-4.

[12]Pons J P,Keriven R,Faugeras O.Multi-view stereo reconstruction and scene flow estimation with a global imagebased matching score[J].International Journal of Computer Vision,2007,72(2):179-193.

[13]Tran S,Davis L.3D surface reconstruction using graph cuts with surface constraints[C]//LNCS 3952:Proceedings of the 9th European Conference on Computer Vision,Graz,Austria,May 7-13,2006.Berlin,Heidelberg:Springer,2006:219-231.

[14]Zaharescu A,Boyer E,Horaud R.TransforMesh:a topologyadaptive mesh-based approach to surface evolution[C]//LNCS 4844:Proceedings of the 8th Asian Conference on Computer Vision,Tokyo,Japan,Nov 18-22,2007.Berlin,Heidelberg:Springer,2007:166-175.

[15]Furukawa Y,Ponce J.Carved visual hulls for image-based modeling[J].International Journal of Computer Vision,2009,81(1):53-67.

[16]Furukawa Y,Curless B,Seitz S M,et al.Manhattan-world stereo[C]//Proceedings of the 2009 Conference on Computer Vision and Pattern Recognition,Miami,USA,Jun 20-25,2009.Washington:IEEE Computer Society,2009:1422-1429.

[17]Furukawa Y,Curless B,Seitz S M,et al.Towards internetscale multi-view stereo[C]//Proceedings of the 23rd Conference on Computer Vision and Pattern Recognition,San Francisco,USA,Jun 13-18,2010.Washington:IEEE Computer Society,2010:1434-1441.

[18]Lewis J P.Fast normalized cross-correlation[J].Vision Interface,1995,10(1):120-123.

[19]Raguram R,Chum O,Pollefeys M,et al.USAC:a universal framework for random sample consensus[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2013,35(8):2022-2038.

[20]Furukawa Y.Patch-based multi-view stereo software[EB/OL].(2014-07-17).http://www.di.ens.fr/pmvs/.

[21]The middlebury computer vision pages[EB/OL].(2014-07-17).http://vision.middlebury.edu/mview/.

[22]Robot vision group pages[EB/OL].(2014-07-17).http://vision.ia.ac.cn/zh/data/index.html.

附中文参考文献：

[6]史颖,王文剑,白雪飞.多特征三维稠密重建方法[J].计算机科学与探索,2015,9(5):594-603.

[7]史利民,郭复胜,胡占义.利用空间几何信息的改进PMVS算法[J].自动化学报,2011,37(5):560-568.

2017-04,Accepted 2017-06.

Improved PMVSAlgorithm with Double Constraints

YANG Wenbo,SUN Bowen+
School of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China
+Corresponding author:E-mail:Sunbw01@163.com

The PMVS(patch-based multi-view stereo)algorithm is widely used in the multi-view stereo field because of its good performance.However,the surface details of the reconstructed model are lost and the exact location of the reconstruction points is not accurate.These problems are very serious in some cases,especially while the input images are few and the texture of the reconstructed model is less.In order to solve these problems,this paper studies the removal of mismatched candidate points and the ranking of seed point reliability:firstly,use USAC(Universal-RANSAC)to remove the candidate matching error;then,put forward the double constraint strategy,meanwhile select the candidate space point which has high reliability as seed.The details of the reconstruction model fit to the original object more.Meanwhile the number of reconstruction points in the model with less texture has been significantly increased and the holes of the texture model are obviously reduced.The validity of the improved algorithm is proven to be more effective and practical.

PMVS algorithm;Universal-RANSAC;double constraints;multi-view stereo reconstruction

10.3778/j.issn.1673-9418.1703097

CNKI网络优先出版:2017-06-27,http://kns.cnki.net/kcms/detail/11.5602.TP.20170627.1246.004.html

YANG Wenbo,SUN Bowen.Improved PMVS algorithm with double constraints.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1804-1815.

A

TP391.9

YANG Wenbo was born in 1989.He is an M.S.candidate at Harbin University of Science and Technology.His research interests include virtual reality and computer simulation,etc.

杨文博（1989—），男，河南安阳人，哈尔滨理工大学计算机科学与技术学院硕士研究生，主要研究领域为虚拟现实，计算机仿真等。

SUN Bowen was born in 1963.He is an associate professor at Harbin University of Science and Technology,and the member of CCF.His research interests include virtual reality and computer simulation,etc.

孙博文（1963—），男，辽宁开元人，哈尔滨理工大学副教授，CCF会员，主要研究领域为虚拟现实，计算机仿真。