循环谱分析在心律失常分类中的应用研究*

褚晶辉，卢莉莉，吕 卫，李 喆

天津大学 电子信息工程学院，天津 300072

循环谱分析在心律失常分类中的应用研究*

褚晶辉，卢莉莉，吕 卫+，李 喆

天津大学 电子信息工程学院，天津 300072

心电信号心律失常分类性能主要取决于有效的特征提取和分类器设计。针对传统心律失常分类研究中，多数研究直接利用时域或者频域特征实现心律失常分类，对于多类别的分类性能仍有待提高。鉴于此，选用循环谱分析方法实现心律失常多分类任务。假设信号处于非平稳状态，建立更符合心电信号实际状态的模型去捕捉心电信号中的隐含周期实现心律失常分类。在提取形态特征和时频域小波系数特征之外，利用循环谱技术提取了谱相关系数特征用于后续多分类任务。除此之外，比较了人工神经网络、传统支持向量机和超限学习机分类器在该实验环境下的分类性能，通过多组对比实验，结果表明，利用循环谱技术结合超限学习机分类器进行心律失常分类，可以区分10类心律失常并在MIT-BIH心律失常数据库上实现了98.13%的平均分类准确率。

心律失常分类；循环谱；超限学习机

1 引言

心电图反映心脏的周期性活动，被心脏科医师广泛应用于心脏类疾病的诊断。心律失常是指由某种活动引起的心脏活动规律异常的现象。由于心电信号的非平稳特性，心脏科医师只通过短时间的心电图波形变化无法准确高效地诊断多类心律失常类型，难以避免误诊漏诊情况。通常来说，即使是同一个人的心电波形在不同运动状态或者不同时刻也会不同，甚至不同类型的心律失常在心电图中呈现相似的形态特征，这增加了人工诊断心律失常的难度。因此，利用计算机进行自动分析和辅助诊断是提高诊断精度和效率的必然趋势。

正常的心电波形图通常包含P波、QRS复合波和T波。其中，P波代表左右心房除极时的电位变化，QRS复合波形代表心室去极化过程中的电位变化，同时描述了心拍的位置、宽度和幅度，T波代表心室复极时的电位变化[1]。心电图中包含的多类心律失常可以总结为五大类，即房性心律失常、室性心律失常、交界性心律失常、心脏传导阻滞性心律失常以及起搏器引起的心律失常等。房性心律失常主要包含房性早搏、异常房性早搏、房性逸搏以及房性扑动。室性心律失常主要包含室性早搏、室性逸搏以及心室颤动。交界性心律失常主要包括交界性早搏和交界性逸搏心拍。心脏传导阻滞性心律失常主要包含左束支传导阻滞以及右束支传导阻滞心拍。准确诊断多类心律失常类型对于临床心脏类疾病的预防和治疗具有重要的意义。

基于信号处理技术的心电图（electrocardiogram，ECG）信号分类方法通常是通过特征提取来选择有效特征或者通过改善分类器设计来提高分类性能。研究人员在心律失常分类算法方面做了大量研究，并取得了不错的进展。其中，Thomas等人[2]提取QRS复合波段的功率、峰态、偏态以及RR间隔特征，并利用双树复小波变换系数结合人工神经网络分类器，将心律失常分为5类。文献[3]对R-T间隔样本数据进行离散小波变换实现心拍分类。除此之外，高阶累积量特征作为非线性特征用于房性心律失常分类[4]，利用线性判别方法取得较好的分类效果。Karaye等人[5]也利用了高阶谱特征对ECG心拍进行分类，并给出双谱图和谱系数图用于分析。除以上特征外，心率变异性（heart rate variability，HRV）特征也常用于心律失常分类，其中Kim等人结合不同分类器将心律失常分为3类[6]，Jovic等人对比使用随机森林和Ada-Boosted C4.5作为分类器将心律失常类型分为9类[7]。基于S变换的方法也用于心律失常检测，Das等人[8]分别使用了基于S变换神经网络（S-transform neural networks，ST-NN）和基于S变换支持向量机分类器进行5类心律失常分类的对比实验。

多数方法均直接利用从时域或者频域提取的特征，忽略了使用非线性变换提取新的特征。目前多数学者提取的特征可以实现心律失常分类，但是对于多分类的性能仍有待提高，因此需要挖掘ECG信号中的隐藏信息提高分类性能。鉴于此，本文采用循环平稳信号分析方法，通过假设信号处于非平稳状态，建立更符合ECG信号实际状态的模型去捕捉ECG信号中的隐含周期用于心律失常分类。分别采用人工神经网络（artificial neural networks，ANN）[2]、支持向量机（support vector machine，SVM）[9]和超限学习机（extreme learning machine，ELM）[10]作为分类器进行多分类心律失常对比实验，结果表明选用本文所提特征可获得更好的分类性能。在实验中，ELM和SVM分类器具有相近的平均分类准确率，同时ELM的分类时间要小于SVM。

本文组织结构如下：第2章介绍心律失常分类特征提取过程；第3章进行实验分析；第4章总结全文。

2 特征提取

ECG信号心律失常分类过程共分为3个步骤：信号预处理，特征提取，模型训练和预测。信号预处理的目的是提高心拍检测精度，鉴于目前一些文献报道的心拍检测算法的检测准确率已经高达99%[11]，本文不再对心拍检测过程进行讨论。本文方法的系统框图如图1所示，主要包含两部分：特征提取和模型训练与预测。

2.1 特征子集

提取ECG信号特征常用处理方法主要是时域分析[12]、频域分析[13]以及时频域分析[14]，这些方法具有较好的二分类效果，但是对于心律失常多分类任务的分类性能仍有待提高。寻找合适的ECG信号特征捕捉ECG信号中隐藏周期，并提取隐藏周期中的隐藏特征信息是更可取的方法。本文使用3种不同类别的特征进行心律失常类型识别，包括形态特征子集、小波变换系数特征子集和谱相关系数特征子集。其中形态特征子集用于捕捉其形态特征，小波变换系数特征子集用于捕捉心电信号时频域特征，谱相关系数特征子集用于捕捉ECG信号中隐藏周期的隐藏特征。

2.1.1 形态特征

QRS复合波特征和RR间隔特征是检测ECG心律失常最直接的两种临床诊断依据。其中，QRS复合波蕴含了心电周期的绝大部分能量，而RR间隔反映了两个连续心电周期的R波峰值间隔变化特征[15]。本文提取前向RR间隔（Pre-RR）、后向RR间隔（Post-RR）、局部RR间隔（Local-RR）、QRS复合波以及T波构成形态特征子集。其中，前向RR间隔是指当前R波和前一个R波之间的间隔，后向RR间隔是指当前R波和后一个R波之间的间隔，局部RR间隔定义如下：

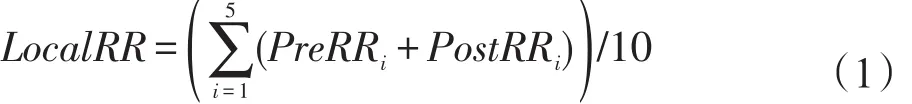
其中，PreRRi(i=1,2,…,5)，PostRRi(i=1,2,…,5)分别表示当前R点的第i个Pre-RR间隔和第i个Post-RR间隔。

2.1.2 离散小波变换系数特征

小波变换在时域和频域具有多尺度分析特性，因此小波变换适合处理时变信号，且多数医学信号均属于时变信号。本文为选择合适的母小波，分别比较了“Coif”、“Sym”、“Db”小波家族，各小波家族的识别准确率如表1所示，其中识别准确率根据式（10）计算，最终选择“Coif4”作为本文实验方法的母小波。对于离散小波变换（discrete wavelet transform，DWT），采样ECG信号x(n)可以表示为：

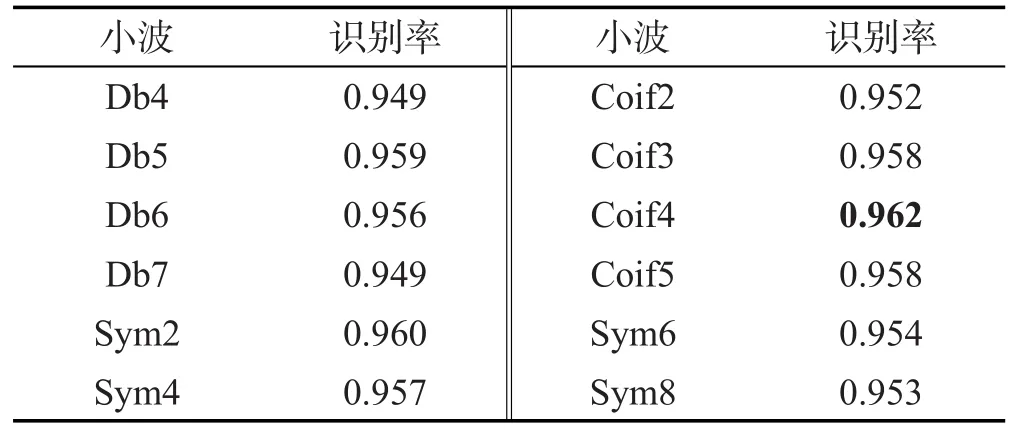
Table 1 Recognition rate comparison of wavelet families表1 小波家族的识别率比较

其中，Ai,k代表第i尺度的概貌信号；Di,k代表第i尺度的细节信号；k是母小波函数的位置。

ECG信号通过DWT进行四尺度分解。已知ECG信号的大部分能量分布在0.5～40 Hz[11]范围，可见小波系数能量主要集中在第3和第4尺度。本文DWT系数特征矢量由第2、3、4尺度的细节系数和第4尺度的概貌系数的归一化标准差、均值、最小值和最大值组成。

2.1.3 谱相关系数特征

大多数的信号分析处理技术中利用的信号是人工合成信号，或是假设信号的统计参数是相对时间固定。实际上，多数待分析信号均具有时变特性。为了获得可靠的信号参数估计，信号应被建模为具有时变统计参数的非平稳过程。循环谱分析即是对非平稳过程信号进行信号分析。循环谱分析的另一个优点是它能够揭示隐藏的信号周期性，离散时间信号x(n)被认为是n阶周期平稳过程，经过n阶的非线性变换之后，它可以被分解成一系列正弦波分量[16]，检测隐藏信息的同时可以去除噪声的影响，因为噪声不存在任何循环统计参数[17]。

心电信号是由心脏肌肉收缩引起的自然周期现象具有近似循环统计参数，因而可被建模为循环平稳过程。本文用二阶统计量即谱相关来描述ECG信号的二阶循环平稳过程。

对于连续时间信号x(t)的非线性变换y(t)在频率f处会产生一条谱线，其中f＞0，在f处的傅里叶变换系数不为0，其计算公式如下：

其中，T是循环周期；f为循环频率。

x(t)的相关函数计算如下：

其中，τ为时延参数。将式（4）带入式（3），可以得到循环自相关函数：

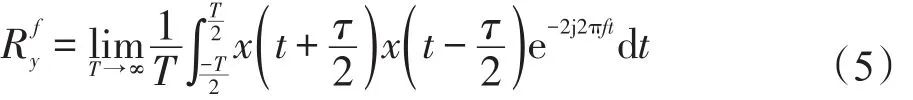
将函数分解为一组具有不同振幅的正弦波是谱分析的主要目的，这种方法可以提取到隐含的信息。谱相关函数是循环自相关函数的傅里叶变换，变换过程如下：

(f0)是关于频率f0和循环频率f的双频平面函数。谱相关平面上若存在f0=f≠0的谱线，则循环自相关具有一阶周期性，而对应的信号x(t)具有二阶周期性。

本文将在循环频率f处的谱相关系数的均值、最大值和方差作为实验的谱相关特征，图2给出了8类典型心律失常对应的谱相关轮廓图。

2.2 分类器

对于心律失常多分类任务，为了有足够的样本数据建立模型，本文使用了MIT-BIH心律失常数据库[18]第一通道的所有心电记录。除选取有效的特征之外，选择合适的分类器，对于精确诊断心律失常类型也是至关重要的。本文的对比实验分别选用人工神经网络、支持向量机和超限学习机作为分类器，并通过实验测试选择各分类器的最佳参数设置。

2.2.1 人工神经网络

人工神经网络（ANN）分类器采用误差反转算法和自适应学习算法可以实现对模型中输入特征和待分类间的映射[19]。传统ANN网络结构一般采用三层架构，输入层、隐含层和输出层。在模型训练学习过程中，一般输入层中的神经元数量取决于输入特征向量的维数，同时输出中的神经元数量等于特征向量所属的类的数量。隐含节点的选择影响着ANN分类器的分类性能，但是目前没有最优的隐含层节点选择技术，一般依靠经验设定。如果神经元数量较少，则建立的神经网络可能不足以对复杂的模型进行建模；如果神经网络的神经元数量过多，可能会导致训练集过拟合问题，降低分类器的泛化能力。由此可见，合理选择神经元数量进行心律失常分类是很有必要的。

2.2.2 支持向量机

Vapnik提出SVM可以用来进行分类任务[9]，但是在多分类任务中使用SVM经常会遇到因不同类别具有相似信息带来的类间不可分问题。为了解决这个问题，许多方法采用多分类策略，常用的策略是一对多分类（one against all，OAA）和一对一策略（one against one，OAO）。两种策略相比，OAA分类策略使用较少的SVM模型，同时具有高效的性能，分类结果至少和其他方法一样准确[20]。因此本文选择LIBSVM（a library for support vector machines）[21]实现SVM，并采用一对多分类策略，进行心律失常分类实验。

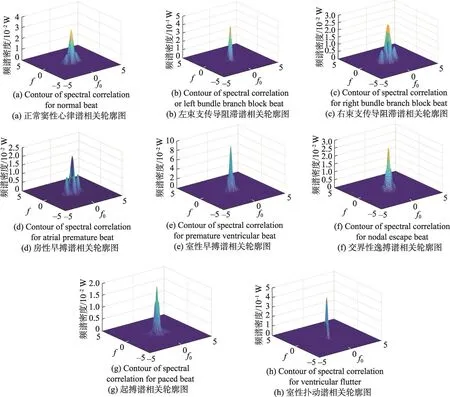
Fig.2 Eight typical types of arrhythmias contour plot for spectral correlation图2 8类典型心律失常谱相关轮廓图

2.2.3 超限学习机

超限学习机属于单隐层前馈神经网络，近年来在许多应用方面取得了不错的进展，其特点是隐层参数均为随机产生，不需要迭代性地调整隐含层参数[10]。对于N个样本的数据集{xi,yi}，其中xi∈R，yi是其对应的标签，ELM的表达式输出为：

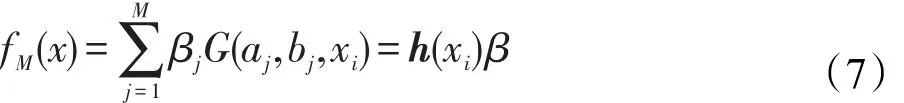
其中，aj、bj分别为第j个隐节点的输入参数；βj是第j个隐节点的输出权值；G(aj,bj,xi)是第j个隐含层节点相应输入变量xi的输出函数；h(xi)是输出函数G的向量形式。

上式可以表示为：

则结合式（7）、式（8）可知，给定任意aj、bj，可以求得β而不必调节隐含层的节点。

ELM算法可以分为3个步骤：

步骤1根据样本分布，通过随机生成隐含层参数(aj，bj)分配隐含层节点。

步骤2计算隐含层输出矩阵H。

步骤3计算输出权重β，β=H-1Y。

3 实验

3.1 ECG数据

样本数据来自MIT-BIH心律失常数据库，包含48条30 min的两通道ECG记录，其中心电信号采样频率为360 Hz。表2给出了MIT-BIH心律失常数据库中心律失常类型和数据分布。多数研究者选用第一通道数据进行训练和性能评估，本文也选用第一通道数据进行实验验证，并选择五折交叉验证方法[22]进行6组对比实验。

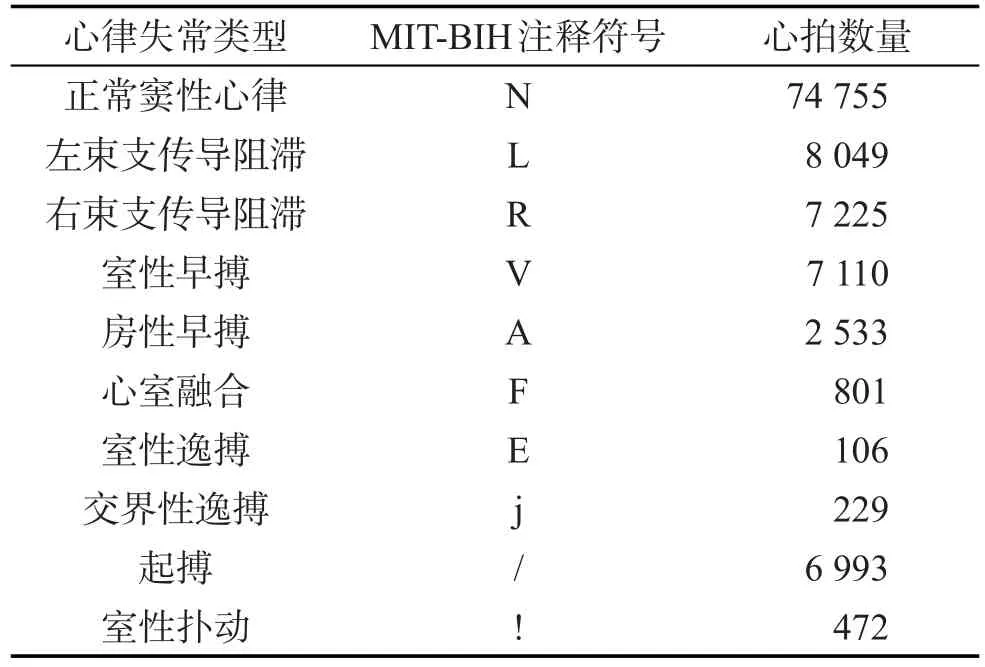
Table 2 Types of arrhythmias and data distribution in MIT-BIH database表2 MIT-BIH数据库心律失常类型及数据分布

3.2 实验结果

本文的分类性能评估准则由准确率(Acc),灵敏度(Sen)和特异性(Spe)组成，其计算公式如下：

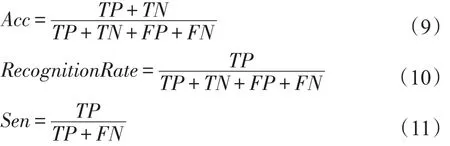
其中，TP是正阳性代表正样本正确分类的数量；FN是负阴性代表为正样本被误分为负样本的数量；TN为正阴性代表负样本正确分类的数量；FP为负阳性代表负样本被错误分类的数量。

为验证本文所提谱相关系数特征的有效性，实验中使用了SVM、ELM、ANN这3种在心律失常分类中表现优异的分类器，分别使用不包含循环谱特征的特征向量(mf+wtf)和包含循环谱特征的特征向量(mf+wtf+csf)进行分类。表3对分类结果进行了对比并给出了每类心律失常类型的灵敏度和特异性情况以及整体平均分类准确率。由表3可以看出，在同一分类器下，带有谱相关系数特征的特征集获得了更好的分类效果，实验表明谱相关系数特征在心律失常分类中的有效性。同时通过表3可知，在3种不同的分类器下，在加入谱相关系数特征后均获得了更好的分类效果，表明了谱相关系数特征具有较好的通用性。

在包含谱相关系数特征的3组实验中，由表3可知，采用ANN分类器获得的平均分类准确率低于SVM和ELM。一般地，ANN分类器在实际应用中对于样本数据间的类别平衡要求较高，且学习过程易陷入局部极小值。在本次实验中，尽管ANN分类器已经取得了较好的分类效果，但是其训练时间较长，且分类效果不如SVM和ELM。

SVM和ELM在本实验条件下获得了相似的平均分类准确率。其中对SVM分类器通过网格寻优进行参数寻优，选择径向基函数为SVM分类器的核函数，核函数中gamma参数设为0.095 5，惩罚因子C设为9.189 6；ELM分类器选择Sigmoid核函数，同时通过多次实验，设置隐含层节点数为3 000。在图3和图4中给出了各自的混淆矩阵，可以得知，SVM作为分类器得到的平均准确率为97.95%，ELM作为分类器得到的平均准确率为98.13%。

从图3和图4中可以看出，L、R、E、j、！以及起搏心拍，这6类心律失常几乎完全可分，但N和V、F、A会产生少数误分类情况，特别是正常窦性心律和房性早搏，观察图2可以发现，两者循环谱轮廓比较相似，且具有相似的谱线分布，仅在幅度上有差别，因此在某些情况下容易产生误分类情况。

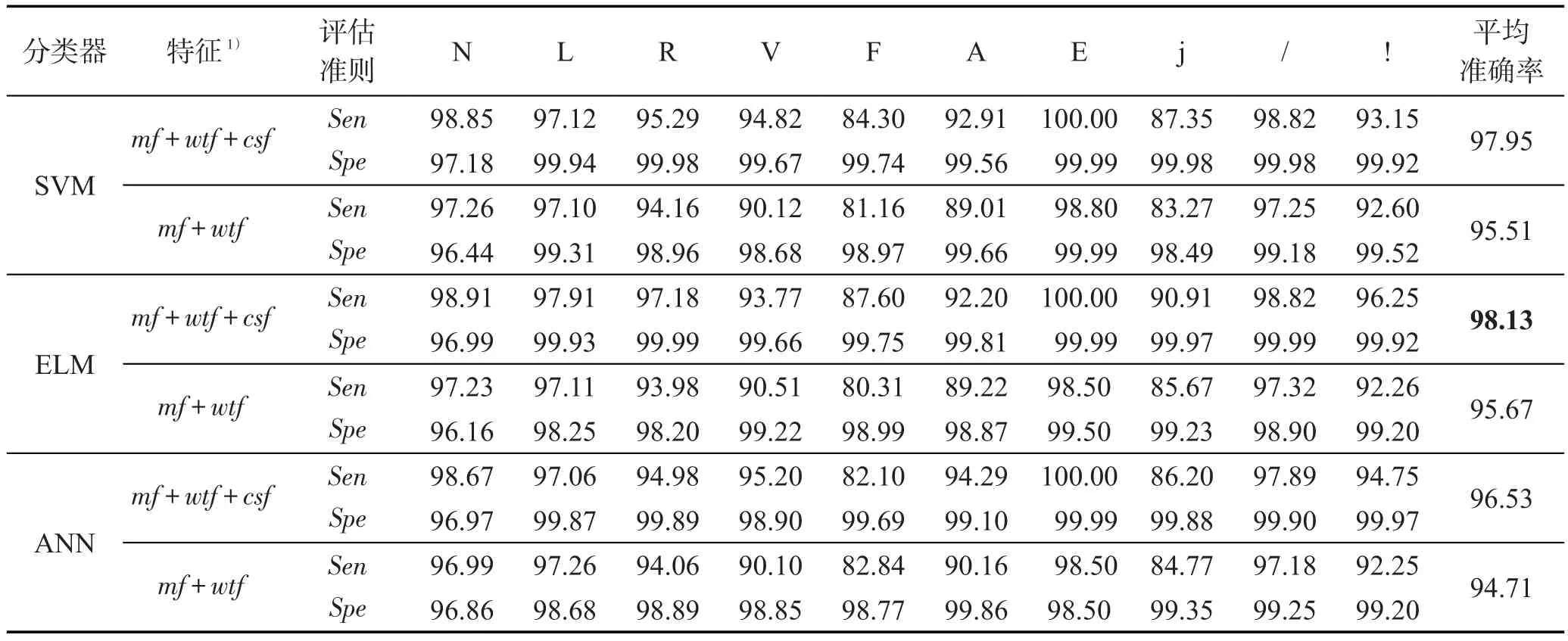
Table 3 Classification performance of six groups of experiments表3 6组实验分类性能比较表 %

Fig.3 Confusion matrix of SVM classifier in MIT-BIH arrhythmia database图3SVM分类器在MIT-BIH数据库上分类混淆矩阵

Fig.4 Confusion matrix of ELM classifier in MIT-BIH arrhythmia database图4ELM分类器在MIT-BIH数据库上分类混淆矩阵

在相近平均分类准确率的情况下，ELM的分类速度快于SVM分类器，因此本文最终选择ELM作为分类器。表4给出了本文方法和其他方法的性能比较结果。将本文方法和其他现有方法进行t-test检验，在检验精度为0.05时，本文实验结果显著性明显(p=0.026 6)，说明本文方法在性能上显著优于其他几种对比方法。表4的实验结果说明本文方法通过利用谱相关技术挖掘隐藏特征具有较高的平均分类准确率，获得了较好的分类性能。

Table 4 Classification accuracy of proposed method compared with other methods表4 本文方法与其他方法平均分类准确率比较表

4 结论

本文将循环谱分析技术用于多类心律失常分类，除提取常用的形态特征和小波系数特征之外，提取了循环谱特征，用于表征形态和时频域不能捕捉的隐藏周期特征。本文分别选取ANN、SVM和ELM作为分类器，进行10类心律失常分类实验。在本实验环境下，SVM和ELM具有相近的平均分类准确率，ELM分类速度快于SVM分类速度，因此最终选择ELM作为本文方法的分类器。实验结果表明，本文的方法在MIT-BIH心律失常数据库上实现了98.13%的平均准确率，相比于其他分类方法，具有更好的分类性能，同时支持更多类型的心律失常分类。

[1]Zhang Wenbo,Li Yuerong.ECG diagnostic manual[M].3rd ed.Beijing:People's Military Medical Press,2007.

[2]Thomas M,Das M K,Ari S.Automatic ECG arrhythmia classification using dual tree complex wavelet based features[J].AEU-International Journal of Electronics and Communications,2015,69(4):715-721.

[3]Saminu S,Özkurt N,Karaye I A.Wavelet feature extraction for ECG beat classification[C]//Proceedings of the 6th International Conference on Adaptive Science&Technology,Ota,Nigeria,Oct 29-31,2014.Piscataway,USA:IEEE,2014:1-6.

[4]Martis R J,Acharya U R,Prasad H,et al.Application of higher order statistics for atrial arrhythmia classification[J].Biomedical Signal Processing&Control,2013,8(6):888-900.

[5]Karaye I A,Saminu S,Özkurt N.Analysis of cardiac beats using higher order spectra[C]//Proceedings of the 6th International Conference on Adaptive Science&Technology,Ota,Nigeria,Oct 29-31,2014.Piscataway,USA:IEEE,2014:1-8.

[6]Kim W S,Jin S H,Park Y K,et al.A study on development of multi-parametric measure of heart rate variability diagnosing cardiovascular disease[C]//Proceedings of the World Congress on Medical Physics and Biomedical Engineering,Seoul,Aug 27-Sep 1,2006.Berlin,Heidelberg:Springer,2007:3480-3483.

[7]Jovic A,Bogunovic N.Evaluating and comparing performance of feature combinations of heart rate variability measures for cardiac rhythm classification[J].Biomedical Signal Processing&Control,2012,7(3):245-255.

[8]Das M K,Ari S.Electrocardiogram beat classification using S-transform based feature set[J].Journal of Mechanics in Medicine and Biology,2014,14(5):396-411.

[9]Vapnik V N.Statistical learning theory[J].Encyclopedia of the Sciences of Learning,2010,41(4):3185-3185.

[10]Huang Guangbin,Zhu Qinyu,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1/3):489-501.

[11]Pan Jiapu,Tompkins W J.A real-time QRS detection algorithm[J].IEEE Transactions on Biomedical Engineering,1985,32(3):230-236.

[12]Javadi M,Arani S AAA,Sajedin A,et al.Classification of ECG arrhythmia by a modular neural network based on mixture of experts and negatively correlated learning[J].Biomedical Signal Processing&Control,2013,8(3):289-296.

[13]Nygards M E,Hulting J.Recognition of ventricular fibrillation utilizing the power spectrum of the ECG[J].Computers in Cardiology,1977:393-397.

[14]Nikias C L.Higher-order spectral analysis[C]//Proceedings of the 15th Annual International Conference on Engineering in Medicine and Biology Society,San Diego,USA,Oct 28-31,1993.Piscataway,USA:IEEE,1993:319.

[15]De C P,Reilly R B.A patient-adapting heartbeat classifier using ECG morphology and heartbeat interval features[J].IEEE Transactions on Biomedical Engineering,2006,53(1):2535-43.

[16]Gardner W A.Cyclostationarity in communications and signal processing[R].Piscataway,USA:IEEE,1994.

[17]Derakhshani M,Le-Ngoc T,Nasiri-Kenari M.Efficient cooperative cyclostationary spectrum sensing in cognitive radios at low SNR regimes[J].IEEE Transactions on Wireless Communications,2011,10(11):3754-3764.

[18]Moody G B,Mark R G.The impact of the MIT-BIH arrhythmia database[J].IEEE Engineering in Medicine&Biology Magazine the Quarterly Magazine of the Engineering in Medicine&Biology Society,2001,20(3):45-50.

[19]Yao Xin.Evolving artificial neural networks[J].Proceedings of the IEEE,1999,87(9):1423-1447.

[20]Rifkin R,Klautau A.In defense of one-vs-all classification[J].Journal of Machine Learning Research,2004,5(1):101-141.

[21]Chang C C,Lin C J.LIBSVM:a library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology,2011,2(3):389-396.

[22]Kohavi R.A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence,Montreal,Canada,Aug 20-25,1995.San Francisco,USA:Morgan Kaufmann Publishers Inc,1995:1137-1143.

[23]Karpagachelvi S,Arthanari M,Sivakumar M.Classification of electrocardiogram signals with support vector machines and extreme learning machine[J].Neural Computing&Applications,2012,21(6):1331-1339.

附中文参考文献：

[1]张文博,李跃荣.心电图诊断手册[M].3版.北京:人民军医出版社,2007.

2016-08,Accepted 2016-12.

ECGArrhythmias Classification with Cyclic SpectralAnalysis*

CHU Jinghui,LU Lili,LV Wei+,LI Zhe
School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China
+Corresponding author:E-mail:luwei@tju.edu.cn

The performance of ECG arrhythmia classification mainly depends on both the effective feature extraction and the optimal design of the classifier.Most of the classic methods extract the time domain features or frequency domain features directly to achieve the arrhythmia classification,but the classification performance still needs to be improved for multi-classification tasks.For this issue,the cyclic spectrum analysis technique is used to achieve the multi-arrhythmia classification.The method assumes that the signal is in non-stationary state,and arrhythmia classification can be implemented through establishing a model to capture the hidden period in the ECG signal,which is more appropriate with the actual state of ECG signals.In order to implement the arrhythmia classification,the morphological features and wavelet coefficients time-frequency domain features are extracted.In addition,the cyclic spectrum technology is adopted for extracting the spectral correlation features for the subsequent multi-classification task.Besides,a comparison on the classification performance is also conducted among the artificial neural networks,the traditional support vector machine classifier and extreme learning machine.Experimental results show that the proposed method based on the extreme learning machine can classify ten types of arrhythmias and achieve an average classification accuracy of 98.13%on the MIT-BIH arrhythmia benchmark dataset.

arrhythmia classification;cyclic spectral;extreme learning machine

10.3778/j.issn.1673-9418.1608083

*The National Natural Science Foundation of China under Grant No.61271069(国家自然科学基金).

CNKI网络优先出版:2016-12-07,http://www.cnki.net/kcms/detail/11.5602.TP.20161207.0922.006.html

CHU Jinghui,LU Lili,LV Wei,et al.ECG arrhythmias classification with cyclic spectral analysis.Journal of Frontiers of Computer Science and Technology,2017,11(11)：1783-1791.

A

TP391

CHU Jinghui was born in 1969.She received the Ph.D.degree in signal and information processing from Tianjin University in 2006.Now she is an associate professor at Tianjin University.Her research interests include digital video technology and pattern recognition,etc.

褚晶辉（1969—），女，天津人，2006年于天津大学获得博士学位，现为天津大学Altera EDA/SOPC联合实验室副教授，主要研究领域为数字视频技术，模式识别等。

LU Lili was born in 1994.She is an M.S.candidate at Tianjin University.Her research interests include digital video technology and pattern recognition,etc.

卢莉莉（1994—），女，内蒙古人，天津大学Altera EDA/SOPC联合实验室硕士研究生，主要研究领域为数字视频技术，模式识别等。发明专利受理2篇。

LV Wei was born in 1976.He received the Ph.D.degree in signal and information processing from Tianjin University in 2003.Now he is an associate professor at Tianjin University.His research interests include digital video technology,embedded system design and pattern recognition,etc.

吕卫（1976—），男，江苏常熟人，2003年于天津大学获得博士学位，现为天津大学Altera EDA/SOPC联合实验室副教授，主要研究领域为数字视频技术，嵌入式系统设计，模式识别等。发表学术论文10余篇，主持国家自然科学基金1项。

LI Zhe was born in 1992.He is an M.S.candidate at Tianjin University.His research interests include data mining,machine learning,pattern recognition and recommender systems,etc.

李喆（1992—），男，山西太原人，天津大学Altera EDA/SOPC联合实验室硕士研究生，主要研究领域为数据挖掘，机器学习，模式识别，推荐系统等。发表科研论文3篇。