基于Schur分解和正交邻域保持嵌入算法的故障数据集降维方法

刘韵佳 赵荣珍 王雪冬

兰州理工大学机电工程学院，兰州,730050

基于Schur分解和正交邻域保持嵌入算法的故障数据集降维方法

刘韵佳 赵荣珍 王雪冬

兰州理工大学机电工程学院，兰州,730050

针对转子故障特征数据集降维问题，提出一种基于Schur分解和正交邻域保持嵌入算法的故障数据集降维方法——Schur-ONPE降维方法。该方法首先应用小波包分解提取不同频带内的能量以组成故障特征值集合，然后运用Schur分解和ONPE算法将高维特征集向低维投影，使降维后类内散度最小化及类间分离度最大化,最后将降维后得到的低维特征集输入K近邻分类器进行模式识别。通过双跨转子试验台的故障特征数据集进行验证，结果表明该方法能够有效地解决转子故障特征集的降维问题。

故障诊断；数据降维；Schur分解；正交邻域保持嵌入算法

0 引言

提取和故障状态识别等。在工程实践中，随着设备复杂度和信息量的增大，人们需要获得的原始特征数据集变得越来越庞大和复杂，这就导致了维数灾难问题，因此，故障特征集维数约简的特征降维问题不可避免地成为基于数据驱动故障诊断技术的一个重要研究方向[2]。

故障振动信号具有很强的非平稳特性，导致故障特征之间往往表现出明显的非线性关系，给降维过程带来了比较大的难度。邻域保持嵌入(neighborhood preserving embedding, NPE) 算法[3]是流形学习中的一种线性降维算法，它能够保持数据在流形上的局部邻域结构，因而得到了广泛应用[4-5]，但NPE算法获取的基特征是非正交的。针对该问题，LIU等[6]提出了正交邻域保持嵌入(orthogonal neighborhood preserving embedding，ONPE)算法，该算法保持了局部邻域内的非线性流形结构及其内在低维特征，是一种能将局部子空间中的保持向量转换为正交基向量的有监督型流形学习算法。然而ONPE算法的正交迭代过程过于繁琐，计算复杂，严重限制了它的应用。

针对上述问题，本文将NPE算法与Schur正交分解技术[7]结合，围绕对ONPE算法的改进开展研究，预期目标是通过将该算法应用于转子故障数据集的降维，为降低故障诊断难度提供理论参考依据。

1 降维算法原理

1.1NPE算法

NPE算法[3]是一种线性降维技术，可以对训练数据进行映射，也可以对测试数据进行估计，同时能够在流形上保持数据的局部邻域结构。用矩阵将局部线性嵌入算法中隐含的非线性映射转变为显式的线性投影，新的样本通过矩阵就可以直接找到嵌入空间中对应的投影点。NPE算法得到的低维空间能够最优地保持原高维空间的局部几何结构，因此可以发现高维空间中的低维流形。该算法的数据处理过程如下。

用数据集X=(x1,x2,…,xN)表示用于学习的训练样本集，其中，元素xi∈RD(i= 1,2,…,N)分别属于C个类，每类有n个训练样本。NPE算法的思想就是最小化目标函数J，并通过线性变换寻找一个最优变换矩阵A，由此可把D维空间的数据映射到一个相对低维的d维空间中(d≪D)，使得样本集X在低维空间的可分性更好。NPE算法认为，如果权值矩阵Wij能在D维空间里重建数据点xi，那么它也可以在d维空间中找到对应的点yi。

NPE算法通式如下：

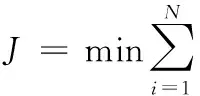
(1)

yi=ATxi

(2)

式中，K表示近邻数。

式(2)所示的线性变换矩阵A可以通过求解最小值问题获得，即

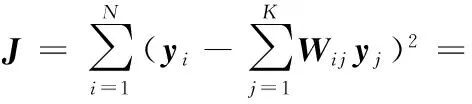
(3)

约束条件为ATXXTA=1,其中，M=(I-W)T(I-W)。

求解式(3)可以转换为求解广义特征向量的最小特征值问题，即

XMXTa=λXXTa

(4)

式中，a是变换矩阵A的基向量。

很明显，XMXT和XXT都是对称的，和半正定的d个最小的非零特征值所对应的特征向量a1，a2，…，ad构成变换矩阵A=[a1a2…ad]。

1.2ONPE算法

ONPE算法能在降维的同时有效地保持样本固有的局部流形结构，可避免局部子空间的结构失真，具有更好的分类能力。该算法能保证模式识别的高精度要求，并且符合特征提取和故障诊断的自动化衔接流程。

依据ONPE算法，则变换矩阵A=[a1a2…ad]可通过求解下式所示的最小值问题得到解决:

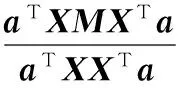
(5)

对应的约束条件如下:

(6)

ONPE算法的计算过程如下：

(1)定义

A(d-1)=[a1a2…ad-1]
S(d-1)=(A(d-1))T(XXT)-1A(d-1)

(2) 迭代计算基向量a1和最小特征向量ad。其中，a1为最大特征值对应的特征向量，ad为下式中J的最小特征值所对应的特征向量:

J(d)=

(I-(XXT)-1A(d-1)(S(d-1))-1(A(d-1))T)(XXT)-1XMXT

(7)

1.3Schur-ONPE算法

ONPE算法的最优矩阵A可以通过求解下式的特征值问题获得:

(XXT)-1XMXTa=λiaλ1<λ2<…<λd

(8)

ONPE算法中使用的是正交迭代理论，其推导过程繁琐,而且计算量较大，而Schur正交分解是通过求解最优向量，得到所需的数据,并没有复杂的理论迭代过程,所以计算也相对简单。

本文利用Schur分解原理[7]，以一种相对简单的方式来解决如何获得正交基向量的问题，由此可以求取出最优的嵌入映射矩阵A：

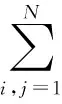
(9)

minJ(A)=mintrace[AT(XXT)-1XMXTA]

(10)

若对式(10)中的(XXT)-1XMXT进行Schur正交分解，则有(XXT)-1XMXT=UTUT，其中，正交矩阵U=[u1u2…uD]，UUT=I，T为上三角对角矩阵，其对角线元素为(XXT)-1XMXT的特征值λ1，λ2，…，λd。若对式(9)所示的目标函数加入约束条件ATXMXTA=I,则正交向量矩阵具有唯一性，即U=V，得

(XXT)-1XMXT=VTVT

即T的d个对角线上元素λ1<λ2<…<λd对应的U中的特征向量为所求的正交投影向量。

(1)主成分分析法(PCA)预处理。为避免因样本特征数大于样本数的情况出现，导致XXT变为奇异矩阵，从而使计算变得更为复杂，可将数据点xi在不丢失本征信息的条件下投影到PCA子空间，使XXT变为非奇异矩阵。将PCA投影矩阵表示为APCA，同时为方便描述，将PCA投影后的矩阵仍用X描述。

(2)构造局部邻域图G并计算权重W。通过K近邻分类器 (K-nearest neighbors classifier，KNNC)[8]对数据集X构造类内、类间邻接图。设G表示有n个节点的邻接图，第i个节点与xi对应，分别在类内和类间寻找与其相近的j个近邻xj，并连接节点i与节点j。若xi与xj属于同类，则xi和xj构成局部邻接矩阵，计算重构权重矩阵Wij。若不属于同类，则权重为零。

(3)构建局部嵌入函数f(a)。用Schur正交分解算法求解正交基函数，可得到最优正交嵌入映射矩阵A。计算训练样本在经Schur-ONPE算法处理后得到的特征值，找出每类故障的聚类中心。利用Schur-ONPE算法得到测试样本的特征值yi=ATxi。

2 故障数据降维方法流程

本文使用的原始数据采集于文献[9]中介绍的双跨度转子试验台，以此试验台测量出的振动信号的集合去构造训练样本和测试样本。利用小波包分析后得到的不同频带范围内的能量，作为高维故障特征集，然后通过本文的算法进行降维处理，从而得到低维敏感故障特征数据集。评判标准为故障分类的辨识准确率。

基于Schur-ONPE算法的故障诊断流程如图1所示。具体流程如下：

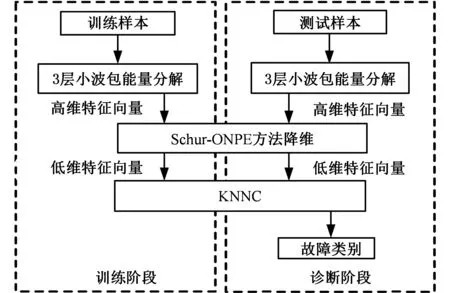
图1 基于Schur-ONPE算法的故障诊断模型Fig.1 Fault diagnosis model based on Schur-ONPE

(1)分别对样本进行3层小波包分解，3层小波分解可以保证更好的频带划分效果，同时兼顾了运行效率;然后求其各个频带范围内的能量，以此作为故障特征信息。

(2)将小波分解后得到的特征信息输入Schur-ONPE算法模型进行训练，然后对样本进行维数约简。

(3)使用KNNC根据训练样本的类标签信息和邻域信息对约简后的测试样本进行故障类别的分类决策。

3 实验结果与分析

在主轴转速为3000 r/min、采样频率为5000 Hz的情况下，对该转子试验平台分别进行了正常转动、轴承松动、质量不平衡、动静碰摩及轴系不对中实验，分别得到以上5种状态振动信号各100组，选取每类状态中的40组作为训练样本，剩余的60组样本作为测试样本。实验振动信号通过布置在转子实验台上的12个电涡流传感器进行采集。对各样本信号进行层数为3的德比契斯(Daubechies)小波函数分解，得到第3层信号的8段频带。具体频带范围见表1。由于样本信号共有12个通道，因此整个样本信号经小波包分解后一共得到12×8=96个能量特征，若将这些特征直接输入分类器，必然会导致分类器识别时间延长、识别正确率降低等问题,因此需要用降维算法去降低故障特征集的空间维度。

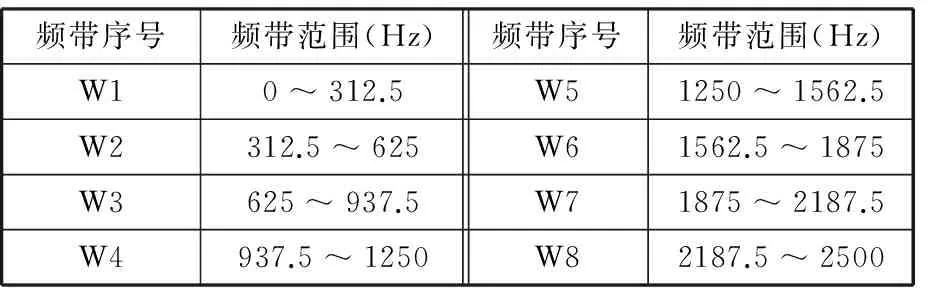
表1 各频带对应的频率范围

为了验证Schur-ONPE降维方法的可行性与有效性，我们同时运用NPE与ONPE两种算法进行实验对比。为了充分涵盖原始数据集的本质信息，将目标维数统一降维到4维(目标维数等于状态类别数减一)，得到测试样本的前两维特征的效果图为图2～图4。

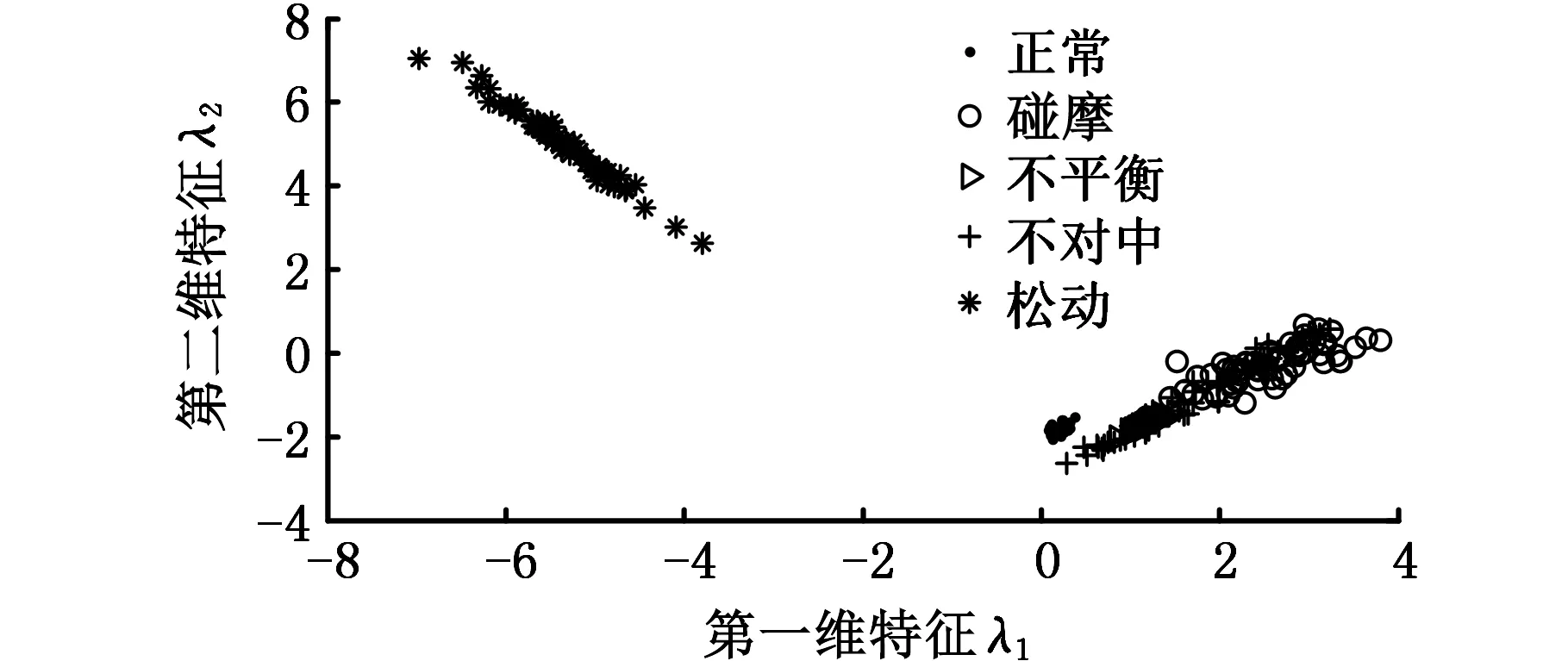
图2 测试样本基于NPE方法降维结果Fig.2 Test sample based on NPE dimension reduction method results

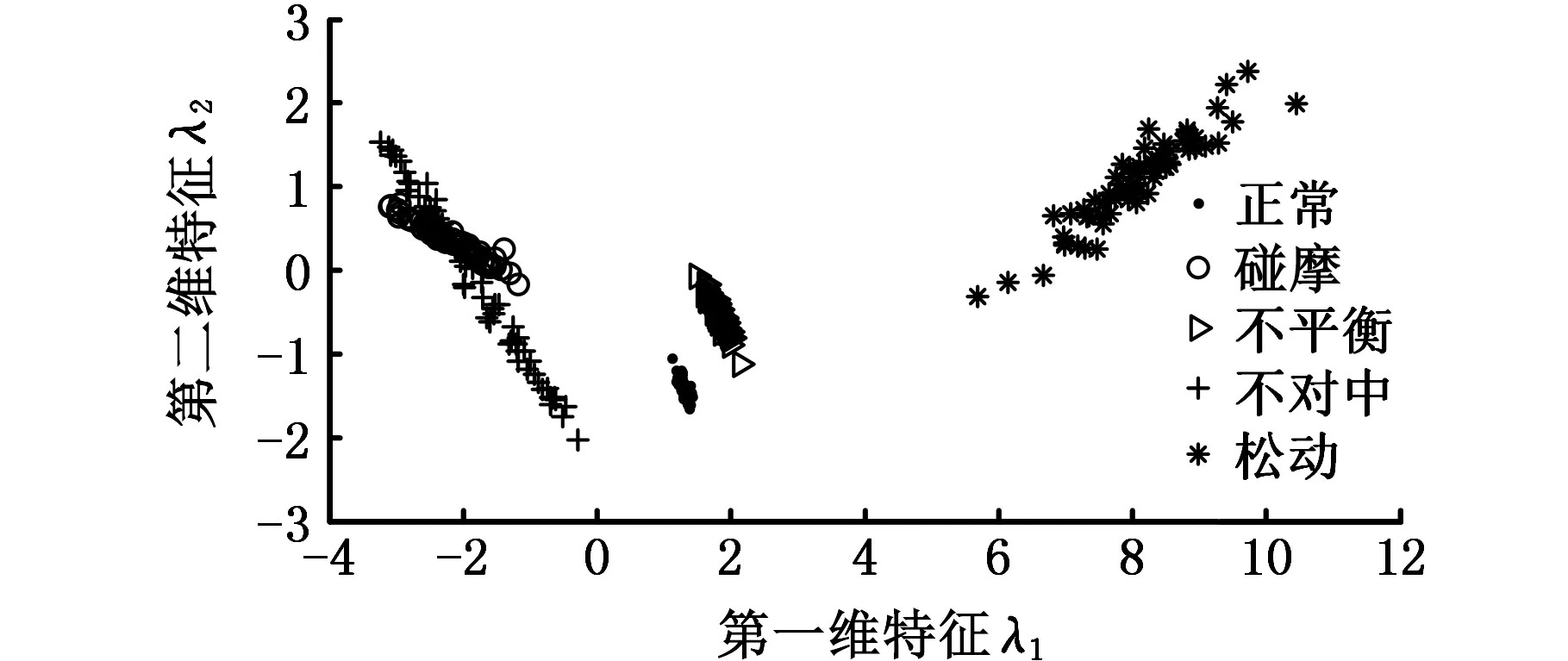
图3 测试样本基于ONPE方法降维结果Fig.3 Test sample based on ONPE dimension reduction method results

图4 测试样本基于Schur-ONPE方法降维结果Fig.4 Test sample based on Schur-ONPE dimension reduction method results

由图2可以看出，使用NPE算法降维后，碰摩故障、不平衡故障以及不对中故障均存在严重的重叠现象，说明碰摩故障、不平衡故障以及不对中故障未能有效分类，只有松动故障的分类效果较好，能够明显与正常情况和其他故障情况区分开。在图3中，基于ONPE算法降维后，只有不对中故障和碰摩故障的数据点发生了明显的混淆重叠现象，说明只有不对中故障和碰摩故障未能有效分类，而松动故障、不平衡故障以及正常状态均得到了良好的分类。而在图4中，使用Schur-ONPE算法能够清晰地辨识出各故障类型，并且聚类效果良好。

为了更客观地描述上述三种方法的降维效果并与原始高维特征集进行比较，本文将NPE、ONPE、Schur-ONPE三种算法降维后得到的特征数据集输入到KNNC中，得到的辨识准确率见表2。对表2进行分析可以得出：

(1)正交的ONPE算法对故障的识别准确率要高于非正交的NPE算法；在正交算法中，Schur-ONPE算法的故障识别率更优秀。

(2)由于原始高维特征集中融入了大量的非敏感以及干扰特征，从而导致识别正确率有所降低。而经过Schur-ONPE算法降维处理的数据，因采用了Schur分解原理，使原有的特征值得到了修正，并进一步去除了原始特征集中相应的干扰信息，因此识别准确率得到了一定的提升。

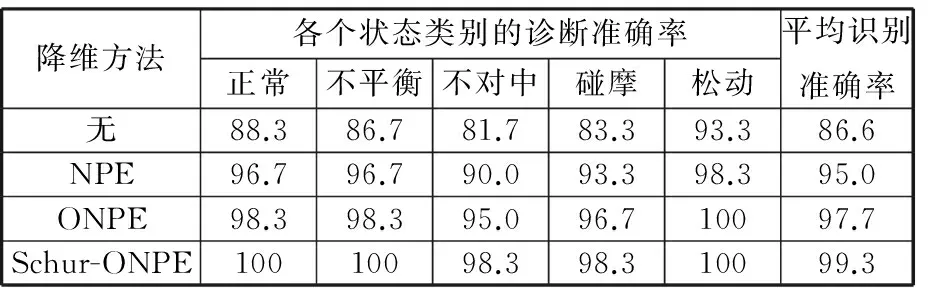
表2 分类辨识方法及其KNNC辨识准确率

(3)ONPE算法计算出的投影向量是通过正交迭代方式得到的，随迭代次数的增加，投影矩阵向量数目也会增加；Schur-ONPE算法的最优向量是通过矩阵正交分解的方式直接获得的，因此运算速度较快，不同程序运行的时间见表3。当诊断数据量增大、故障类型增多时Schur-ONPE算法将具有更大的优势。

表3不同算法的特征提取时间

Tab.3Featureextractiontimefordifferentalgorithmss

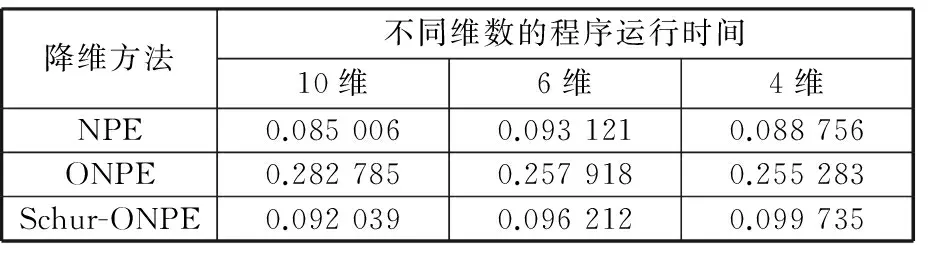
降维方法不同维数的程序运行时间10维6维4维NPE0.0850060.0931210.088756ONPE0.2827850.2579180.255283Schur-ONPE0.0920390.0962120.099735

为了提高算法的泛化能力，将不同算法在不同转速下的数据集输入KNNC 分类器中，得到的平均辨识准确率见表4。

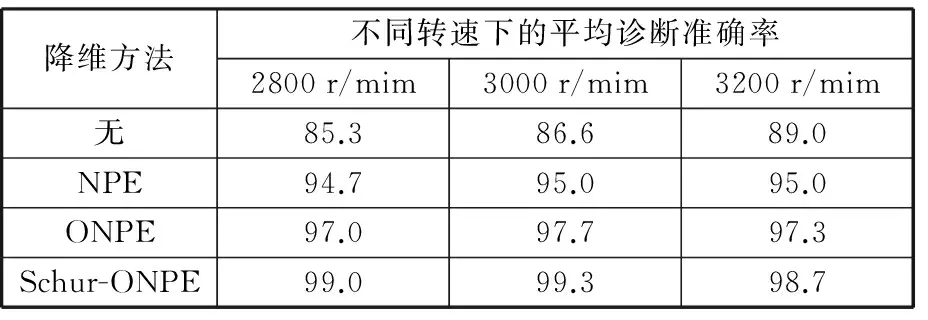
表4 不同算法的在不同转速下的KNNC辨识准确率

由表4可以看出，在不同转速下Schur-ONPE降维方法的平均识别正确率都优于NPE算法和ONPE算法，说明Schur-ONPE算法具有良好的适用性。

4 结语

提出一种基于Schur分解和正交邻域保持嵌入(ONPE)相结合的故障数据集降维方法——Schur-ONPE算法。首先将原始振动信号进行3层小波包分解并构造高维特征向量，再利用Schur-ONPE算法训练出最佳分类特征集，将高维特征向量约简为可分性更好的低维本征向量，并输入到KNNC 分类器中进行故障识别。通过双跨转子试验台进行故障模拟实验，并与NPE、ONPE等方法进行实验数据对比，结果表明， ONPE算法的平均识别率比NPE算法的平均识别率提高了2.4%，而Schur-ONPE算法的故障平均识别率又比ONPE算法的故障平均识别率提高了1.7%。通过对算法运算时间的对比，Schur-ONPE算法的运算效率也比ONPE算法的运算效率提高了36.31%，而且在不同转速下也都能达到良好的效果。因此，本研究提出的Schur-ONPE算法能有效地进行故障特征集降维。本研究可为解决旋转机械故障数据集的降维问题提供一种新的解决思路。

[1] WANG H,CHAI T,DING J.Data Driven Fault Diagnosis and Fault Tolerant Control：Some Advances and Possible New Oirections[J].Acta Automatica Sinica,2009,35(6):739-747.

[2] 王雪冬,赵荣珍,邓林峰.基于KSLPP与RWKNN的旋转机械故障诊断[J] .振动与冲击,2016, 35(8):219-223.

WANG Xuedong, ZHAO Rongzhen, DENG Linfeng. Rotating Machinery Fault Diagnosis Based on KSLPP and RWKNN[J]. Journal of Vibration & Shock, 2016, 35(8):219-223.

[3] HE X,CAI D,YAN S,ZHANG H. Neighborhood Preserving Embedding[J]//IEEE International Conference on Computer Vision, 2005,2(23): 1208-1213.

[4] 孙健,王成华,杜庆波.基于小波包能量谱和NPE 的模拟电路故障诊断[J] .仪器仪表学报,2013,34(9)：2021-2027.

SUN Jian, WANG Chenghua, DU Qingbo. Analog Circuit Fault Diagnosis Based on Wavelet Packet Energy Spectrum and NPE[J]. Chinese Journal of Scientific Instrument, 2013,34(9)：2021-2027.

[5] 杜海顺,柴秀丽,汪凤泉，等. 一种领域保持判别嵌入人脸识别方法[J] .仪器仪表学报,2010,31(2):625-629.

DU Haishun, CHAI Xiuli, WANG Fengquan, et al. Face Recognition Method Using Neighborhood Preserving Discriminant Embedding[J]. Chinese Journal of Scientific Instrument, 2010,31(2):625-629.

[6] LIU X M,YIN J W,FENG Z L,et al．Orthogonal Neighborhood Preserving Embedding for Face Recognition[C]//Proceedings of 2007 IEEE International Conference on Image,ICIP 2007. New York,2007:133-136.

[7] 王广斌,刘义伦,黄良沛.基于核Schur正交局部Fisher判别的转子故障诊断[J]. 仪器仪表学报,2010,31(5):1005-1009．

WANG Guangbin, LIU Yilun, HUANG Liangpei. Rotor Fault Diagnosis Based on Kernelschur-orthogonal Local Fisher Discriminant[J]. Chinese Journal of Scientific Instrument, 2010,31(5):1005- 1009．

[8] 孙斌,刘立远,牛翀. 基于局部切空间排列和最近邻分类器的转子故障诊断方法[J].中国机械工程,2015, 26(1):74-78.

SUN Bin, LIU Liyuan, NIU Chong. Rotor Fault Diagnosis Methods Based on Local Tangent Space Alignment and K-nearest Neighbor[J]. China Mechanical Engineering, 2015, 26(1):74-78.

[9] 霍天龙,赵荣珍,胡宝权. 基于熵带法与PSO优化的SVM转子故障诊断[J].振动、测试与诊断,2011,31(3):279 -284.

HUO Tianlong, ZHAO Rongzhen, HU Baoquan. Fault Diagnosis for Rotor Systems Based on Entropy Band Method and Support Vector Machine Optimized by PSO[J]. Journal of Vibration Measurement & Diagnosis, 2011, 31(3):279-284.

FaultDataSetDimensionReductionMethodBasedonSchurDecompositionandONPEAlgorithm

LIU Yunjia ZHAO Rongzhen WANG Xuedong

School of Mechanical and Electronical Engineering，Lanzhou University of Technology,Lanzhou，730050

Aiming at dimension reduction of fault data set，a novel method in dimension reduction was proposed based on the combination of Schur decomposition and ONPE algorithm. Firstly wavelet packet decomposition was used to extract the fault signals of different frequency band energy features，then Schur decomposition and ONPE algorithm were used to project the high-dimensional data sets to lower dimensions. After the transformation, the considered pairwise samples within the same class were as close as possible, while those between classes were as far as possible. Finally, the lower dimension was collected and the K nearest neighbor classifier was input to recognize the different patterns. The fault characteristic data sets from a double span rotor test-rig were used to validate the proposed algorithm performances. The results show that this method may solve the problems of reducing the dimension of rotor fault features sets effectively.

fault diagnosis; data dimension reduction; Schur decomposition; orthogonal neighborhood preserving embedding(ONPE) algorithm

TH165；TP18

10.3969/j.issn.1004-132X.2017.21.006

2016-08-16

国家自然科学基金资助项目(51675253)

(编辑苏卫国)

刘韵佳，女，1989年生。兰州理工大学机电工程学院硕士研究生。研究方向为旋转机械故障诊断。赵荣珍(通信作者)，女，1960年生。兰州理工大学机电工程学院教授、博士研究生导师。E-mail：zhaorongzhen@lut.cn 。王雪冬，男，1988年生。兰州理工大学机电工程学院硕士研究生。