基于正态模糊时间窗约束的飞机装配物料配送路径规划

朱永国 李俊杰 刘春锋 宋利康

1.南昌航空大学航空制造工程学院，南昌，3300632.南昌航空大学信息工程学院，南昌，330063 3.江西洪都航空工业集团有限责任公司部装一厂，南昌，330024 4.江西洪都航空工业集团有限责任公司经理部，南昌，330024

基于正态模糊时间窗约束的飞机装配物料配送路径规划

朱永国1李俊杰2刘春锋3宋利康4

1.南昌航空大学航空制造工程学院，南昌，3300632.南昌航空大学信息工程学院，南昌，330063 3.江西洪都航空工业集团有限责任公司部装一厂，南昌，330024 4.江西洪都航空工业集团有限责任公司经理部，南昌，330024

针对飞机装配过程中装配工位物料需求时间模糊化现象，提出基于正态模糊时间窗约束的工位物料需求时间参数表征方法，用正态模糊数的隶属度表示工位的满意度。建立了基于正态模糊时间窗约束的飞机装配物料配送路径规划数学模型，并采用遗传算法进行了求解。遗传算法的选择算子利用轮盘赌和最优保留策略，交叉算子采取小生境选择机制的双选择交叉策略，变异算子确保每代个体得到进化。MATLAB仿真结果表明，该规划方法拥有较好的经济效益。

飞机装配；物料配送；正态模糊数; 路径规划

0 引言

由于生产波动，装配物料配送过程中经常会出现工位物料需求时间模糊化现象。工位物料需求时间模糊化直接影响整个物料配送的时效性，这种问题可被称为模糊车辆路径问题(vehicle routing problem,VRP)。为了解决这一难题，CHENG等[1]、LI等[2]、ALI[3]分别针对模糊预约时间、模糊路径和模糊运输的VRP进行了研究。张建勇等[4]采用三角模糊数的隶属度来反映客户收货的满意情况。李晋航等[5]在考虑工位物料需求量、行驶时间和预约时间窗不确定性的基础上，以三角模糊数表征不确定性参数。朱晓锋等[6]、陈钢铁等[7]分别针对多车型VRP，以三角模糊数表征不确定性参数。杨翔等[8]针对模糊时间窗的多中心开放式VRP，构建梯形模糊时间窗隶属函数来表征时间参数。三角模糊数的隶属度函数和梯形模糊数的隶属度函数均属于线性函数，不能反映物料需求随实际情况的变化。严正锋等[9]以物料到达工位的时间模糊隶属函数反映工位的满意度，王旭坪等[10]通过时间窗模糊化处理，将顾客服务的满意度量化为配送服务开始时间的模糊隶属度函数，他们构造的函数属于非线性函数，但函数构造过程需要大量历史经验和生产数据。马磊磊等[11]采用正态分布表示工位的满意度函数，建立了工位预约时间条件下的数学模型，但是没有给出正态分布中参数σ2的求解公式。

飞机装配是一项复杂的系统工程，具有产品装配层级多、装配工位多、装配周期长、装配工艺复杂、工序离散多变等特点[12-13]。飞机装配过程中，工人的熟练程度、装配技术水平以及装配单元的复杂程度等不确定性因素都会影响装配节拍的快慢，导致工位需求物料时间不确定[14-15]，因此，飞机装配的物料配送问题比一般车辆路径问题更突出。为此，本文针对飞机装配物料需求时间模糊VRP，提出用正态模糊数来表征工位物料需求时间参数，研究基于正态模糊时间窗约束的飞机装配物料配送路径规划方法。

1 基于正态模糊时间窗约束的工位物料需求时间数学模型

传统时间窗通常仅给出工位需要物料的起始时间和终止时间，物料在起始时间至终止时间范围内到达就会被认为满足要求。但由于存在生产波动，传统时间窗不能准确反映工位物料需求时间偏好的满意度。模糊时间窗是依据物料配送时间对工位满意程度的影响进行模糊量化得到的，模糊时间窗用模糊数表征，模糊数用隶属函数所定义的正规凸模糊集表示。工程实际中，由于飞机装配过程中生产节拍的变动，工位需要物料的期望时间也会发生相应的变化。物料到达时间与期望时间越接近，工位的满意度越高，满意度最大值为1；物料到达时间离期望时间越远，工位的满意度越低，满意度最小值为0。飞机批量装配时，物料到达工位的配送时间往往呈正态分布，因此，虽然三角和梯形等模糊数可以表示不同时间物料到达工位的满意度，但是其工位物料配送时间的满意度与正态分布配送时间的隶属度契合度不高。与三角和梯形等其他模糊数相比较，正态模糊数的隶属度与批量生产工位的满意度契合度更高，故可采用正态模糊数对飞机装配物料配送时间进行约束，以反映实际飞机装配中物料到达工位时间的满意度。在确保工位满意度的同时，减少配送成本，提高飞机装配效率。

为此，采用正态模糊时间窗约束表示工位物料需求时间，即用正态模糊数表征工位物料需求时间参数，用模糊数的隶属函数表示工位配送时间的满意度。假设工位i物料需求时间为[tsi，tei]，tsi、tei分别为可以接受的物料到达工位i的起始时间和结束时间。依据文献[16]，建立基于正态模糊数的物料需求时间满意度数学模型：

(1)

式中，ti为物料到达工位i的配送时间；μi为ti的均值，μ=(tsi+tei)/2；σi为ti的方差，σi=(tei-tsi)/6；μ(ti)为ti的隶属度，μ(ti)∈[0,1]。

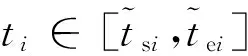
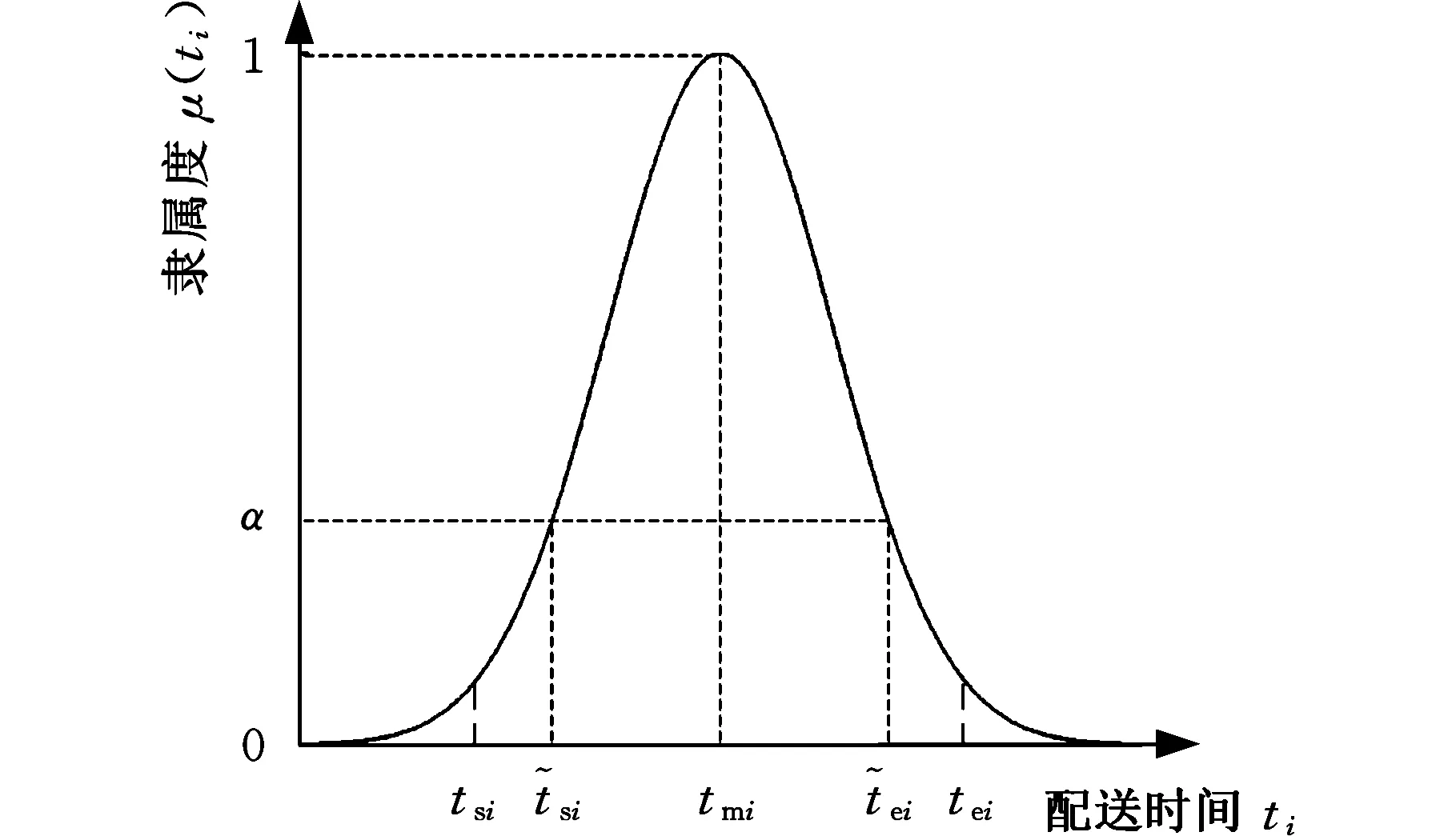
图1 工位i在满意度为α时物料配送时间窗Fig.1 Time window for material delivery of workstation i when confidence level is α

2 基于正态模糊时间窗约束的物料配送路径规划

飞机装配物料主要由配送中心的K种类型车辆进行配送，设第k(k=1，2，…，K)种类型辆车最大的载重量为Qk,最大的行驶距离为Dk。配送过程中，各工位物料的配送量和服务时间窗已知，每种类型车辆所负责工位的物料配送量qi之和不大于Qk，而且各工位只能在服务时间窗内由一种类型车辆服务一次。每种类型车辆从配送中心出发，完成所有任务的车辆必须返回配送中心。利用构建的物料配送正态模糊时间窗约束数学模型，以总配送费用为优化目标，建立基于正态模糊时间窗约束的物料配送路径规划数学模型：

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

yik∈{0,1}xijk∈{0,1}

(10)

i，j=1，2，…，N

式中，N为需要配送的工位总数；ck为k类型车辆的固定成本；xk为k类型车辆的使用数量；vk为k类型车辆单位距离的运输成本；dij为从工位i到工位j的行驶距离；tij为从工位i到工位j的行驶时间；si为工位i的服务时间；yik为0-1类型的工位决策变量，一辆k型车辆服务工位i时，yik=1，否则yik=0；xijk为0-1类型的车辆决策变量, 一辆k型车辆从工位i驶向工位j时，xijk=1，否则xijk=0。

式(2)是以最小总配送费用为目标的路径规划函数。式(3)表示工位i需要物料时间要满足正态模糊数的置信度α。式(4)表示置信度为α时，工位j所需求配送物料的起始时间和结束时间。式(5)表示工位i需求配送量不大于车辆最大载重量。式(6)、式(7)表示每个工位由一辆车配送，且服务一次。式(8)表示每辆车从配送中心出发，完成配送任务返回配送中心。式(9)表示每辆车的行驶距离不能超过其最大值限制。

3 基于遗传算法的物料配送路径规划模型求解

3.1染色体编码

常用的染色体有二进制、符号和自然数3种编码方法。与其余两种编码方法相比，自然数编码方法具有较高的计算效率，因此，运用自然数编码方法对染色体进行编码。染色体R=(1，i1，i2，…，ij，1，im，…，ik，1，…，1)，其中，整数ij表示某段路径的第j个工位点，1表示配送中心。染色体编码首尾要求都是“1”，则共有为n+1个“1”。染色体编码被“1”分成n组，即n段路径，表示配送路径方案由n辆车来完成所有的配送任务。子路径之间是无序的，而子路径内部是有序的。

3.2适应度计算

初始群体按照编码方法生成配送路径方案。编码方法应符合配送车辆问题的特征，隐含每个工位点仅由一辆车配送，且配送服务一次的约束条件。在载重量、行驶距离和物料需求正态模糊时间窗约束的限定下，迭代遗传操作不一定能获得合理的配送路径方案。为此，针对染色体R表示配送路径方案可行性，引入惩罚函数

(11)

式中，ce为早到惩罚成本；cl为晚到惩罚成本。

利用PW计算R的适应度函数：

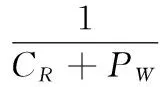
(12)

式中，CR为染色体R所表示的该段路径规划函数值。

3.3遗传操作

3.3.1算子筛选

运用轮盘赌确定染色体的条数。在0～1范围内产生随机数，如果随机数不大于个体的选择概率，就将该个体选为计算对象；否则就忽略。最后，再利用最优保留策略加快收敛速度。

3.3.2交叉算子

选择个体交叉前设定某个阈值，为了避免个体陷入局部最优，即小生境选择机制。在选择染色体交叉点的时候，选择虚拟配送中心之间的子串，即1基因码之间的子串。若两条都没选中1基因码之间的子串，则重新选取。个体交叉方法采用传统的顺序交叉，图2所示为交叉操作过程。

图2 交叉操作Fig.2 Crossover operation

3.3.3变异算子

变异操作通常按照变异概率进行，根据实际问题需要，随机选择除1基因码外，同一条染色体不同组内产生两个基因位，将选定两点的基因码进行交换，得到新子个体来替代变异前的父体，从而完成变异。图3所示为变异操作过程。

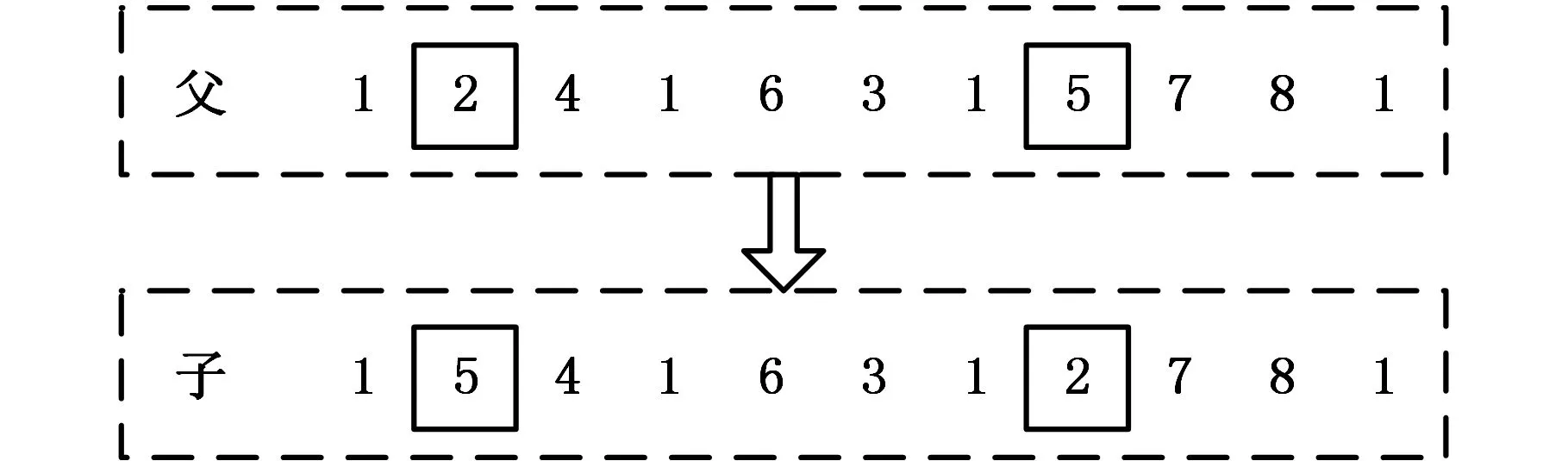
图3 变异操作Fig.3 Mutation operation

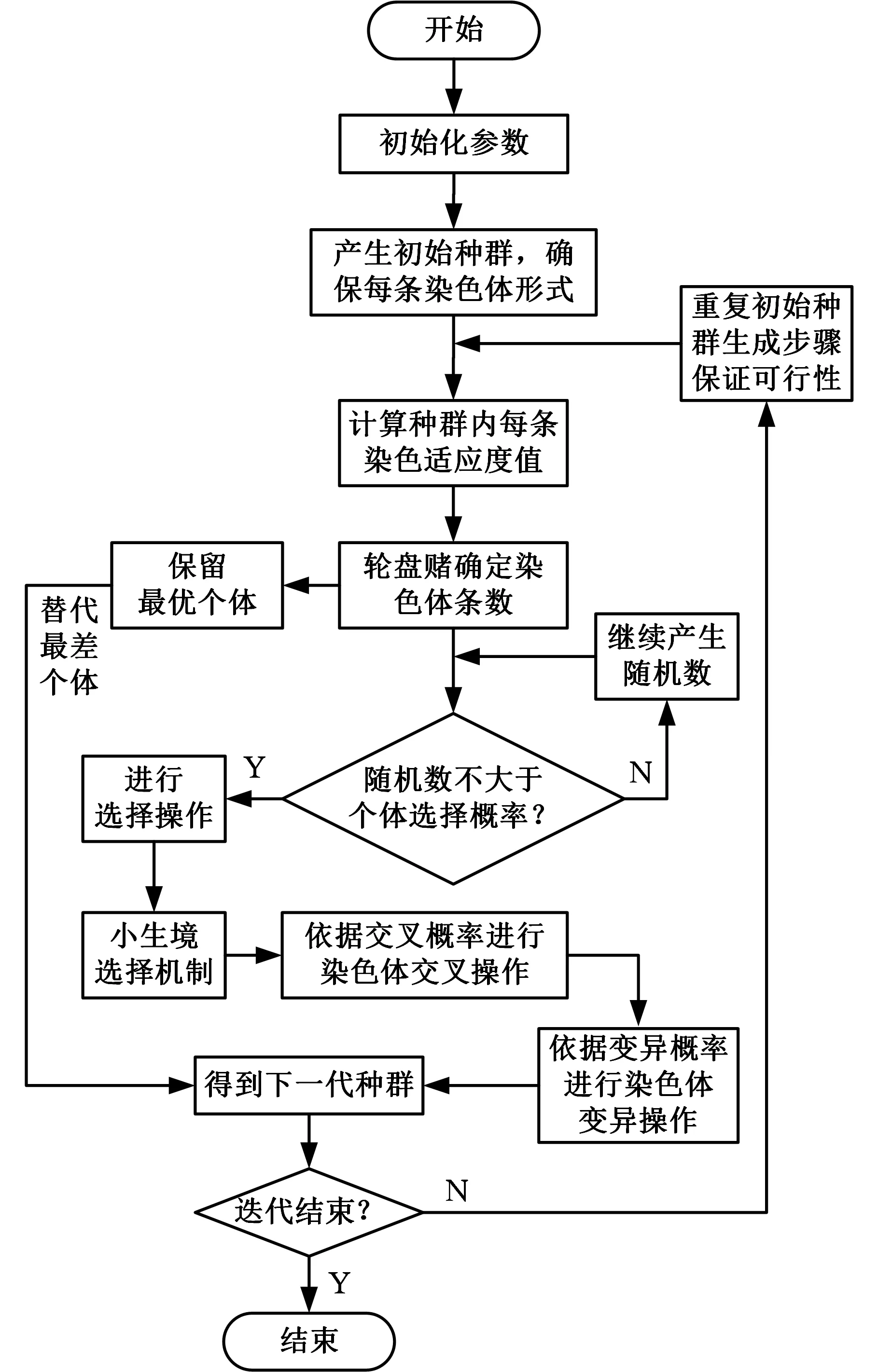
图4 遗传算法流程图Fig.4 Flow chart of genetic algorithm

3.4算法步骤

利用遗传算法，规划模型求解流程如图4所示。具体步骤如下。

(1)初始化如下参数：车辆类型K，最大载重量Qk和最大行驶距离Dk；工位数N，工位需求配送量qi，需求物料时间范围[tsi,tei]；迭代次数G，染色体数量P，交叉概率Pc和变异概率Pm。

(2)按照自然数编码方法产生初始种群，确保每条染色体的形式为R。

(3)计算种群内每条染色体适应度FR。

(4)根据本代每条染色体的适应度，计算种群内每条染色体占群体适应度的比例，然后运用轮盘赌生成下一代染色体，再完成最优保留策略。

(5)依据小生境选择机制，挑选出符合条件的两条父染色体，再根据交叉概率Pc，完成交叉操作。

(6)依据变异概率Pm完成变异操作，得到新染色体。

(7)保留最优的个体替代种群中最差的个体，产生下一代种群。

(8)如果满足迭代次数，则输出计算结果；否则返回步骤(3)继续遗传操作。

4 工程应用实例研究

针对我国自主研制的某型高级教练机的条装配生产线的物料配送路径规划进行工程应用研究。该装配生产线需要从配送中心配送9种零件到装配生产线的9个工位，将配送中心工位编号设定为1，装配生产线的9个工位编号分别为编号2、编号3、…、编号10，图5为配送中心与工位位置关系简图。配送中心共有3种类型配送车辆，每种类辆车最大行驶距离为50 km。第1种类型车辆有2辆，最大载重量为500 kg，固定成本为50元，含配送小组人工费、车辆运输费等在内的单位距离运输成本为40元/km；第2种类型车辆有3辆，最大载重量为1000 kg，固定成本为100元，含配送小组人工费、车辆运输费等在内的单位距离运输成本为80元/km；第3种类型车辆有1辆，最大载重量为1500kg，固定成本为150元，含配送小组人工费、车辆运输费等在内的单位距离运输成本为120元/km。

图5 配送中心与工位位置关系简图Fig.5 Simplified map between distribution center and work station location

为保证行驶安全，每种类型配送车辆速度为60 m/min；每早到1 min的惩罚成本为10元，每迟到1 min的惩罚成本为10元。各工位配送需求情况如表1所示，配送中心与各工位之间的距离如表2所示。配送过程中要求每辆车不超载、不超最大行驶距离，而且在满足每个工位的需求物料时间和需求配送量前提下，安排车辆行驶路线使得总配送费用最少。由文献[4，7，10]可知，采用三角模糊数表征时间参数比传统时间窗具有较好的配送效率。为此，采用MATLAB软件对正态模糊数时间窗、三角模糊数时间窗和传统时间窗的三种路径轨迹方法进行综合比较。

表1 各工位物料配送需求

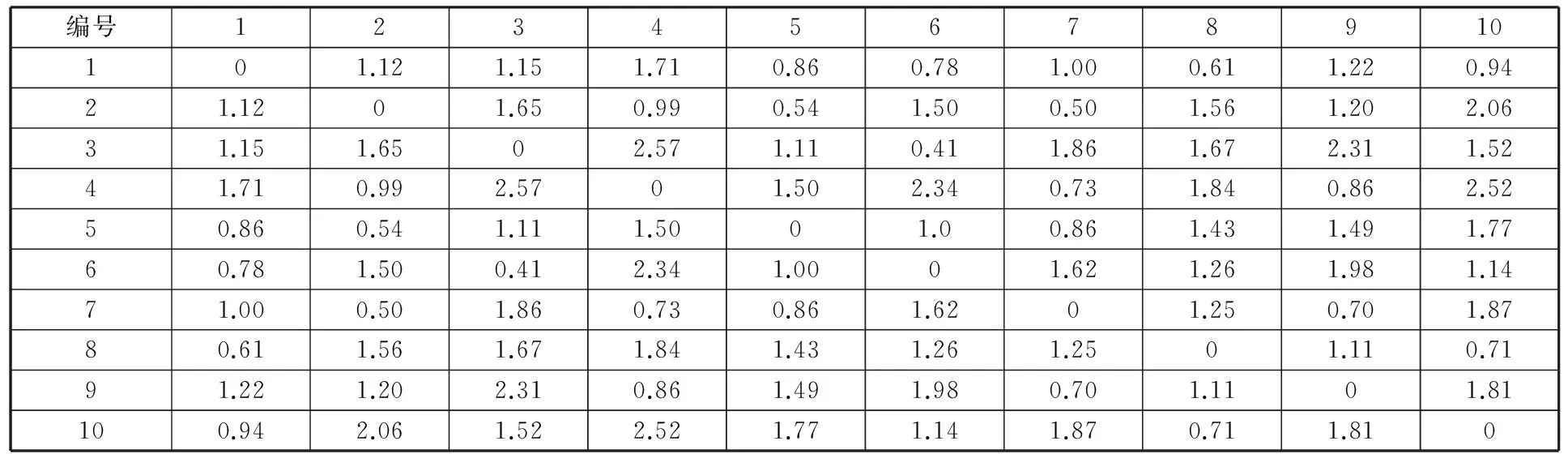
表2 配送中心与各工位之间的距离

设置算法参数，种群大小为80，迭代次数终止设定为100，交叉概率为0.6，变异概率为0.05。当置信度α取0.2、0.4、0.6、0.8时，计算结果如表3、表4所示。

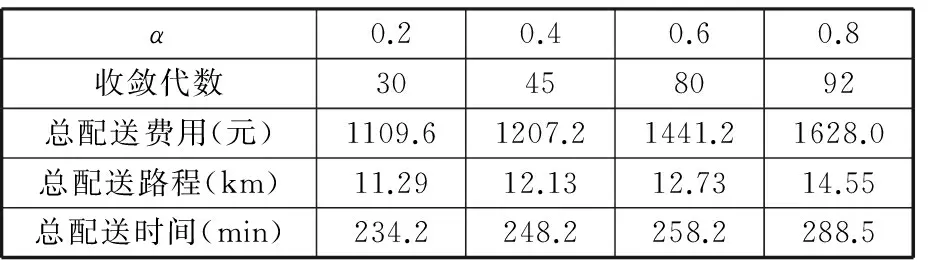
表3 正态模糊时间窗约束不同数置信度计算结果

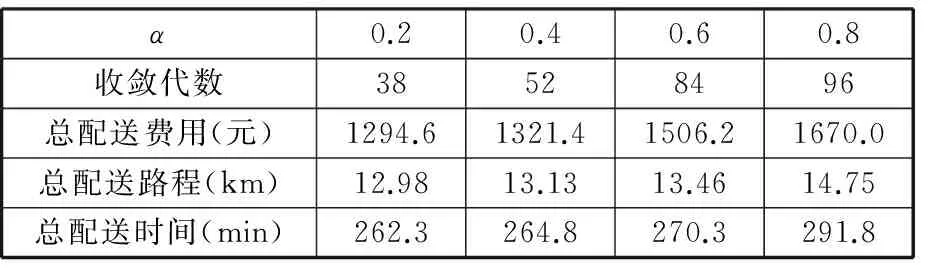
表4 三角模糊时间窗约束不同数置信度计算结果

由表3、表4可知，α取0.2、0.4、0.6、0.8时，正态模糊数方法比三角模糊数方法的总配送费用分别减少了185.2元、114.2元、85元和42元，减少的费用占总配送费用比例分别为16.7%、9.5%、5.9%、2.6%，随着置信度的增大，两种方法总配送费用的差距逐渐减小，相应的总配送路程和总配送时间的差距也逐渐减小。由表3、表4还可看出，置信度取值对问题求解的迭代收敛速度有明显影响，即α越大，配送车辆到达工位的时间可选择范围就越小，因而产生额外的费用，不利于配送路径的优化。为此，应选取置信度α=0.2，该置信度水平下配送车辆到达工位的时间可选择范围最大，找到目标函数最优解的可能性也最大。

当初始种群大小为80，迭代次数终止设定为100，交叉概率为0.6，变异概率为0.05，采用传统时间窗方法进行求解，同时选取置信度α=0.2时，分别对正态模糊、三角模糊时间窗轨迹规划方法进行求解，得到图6所示的迭代结果。

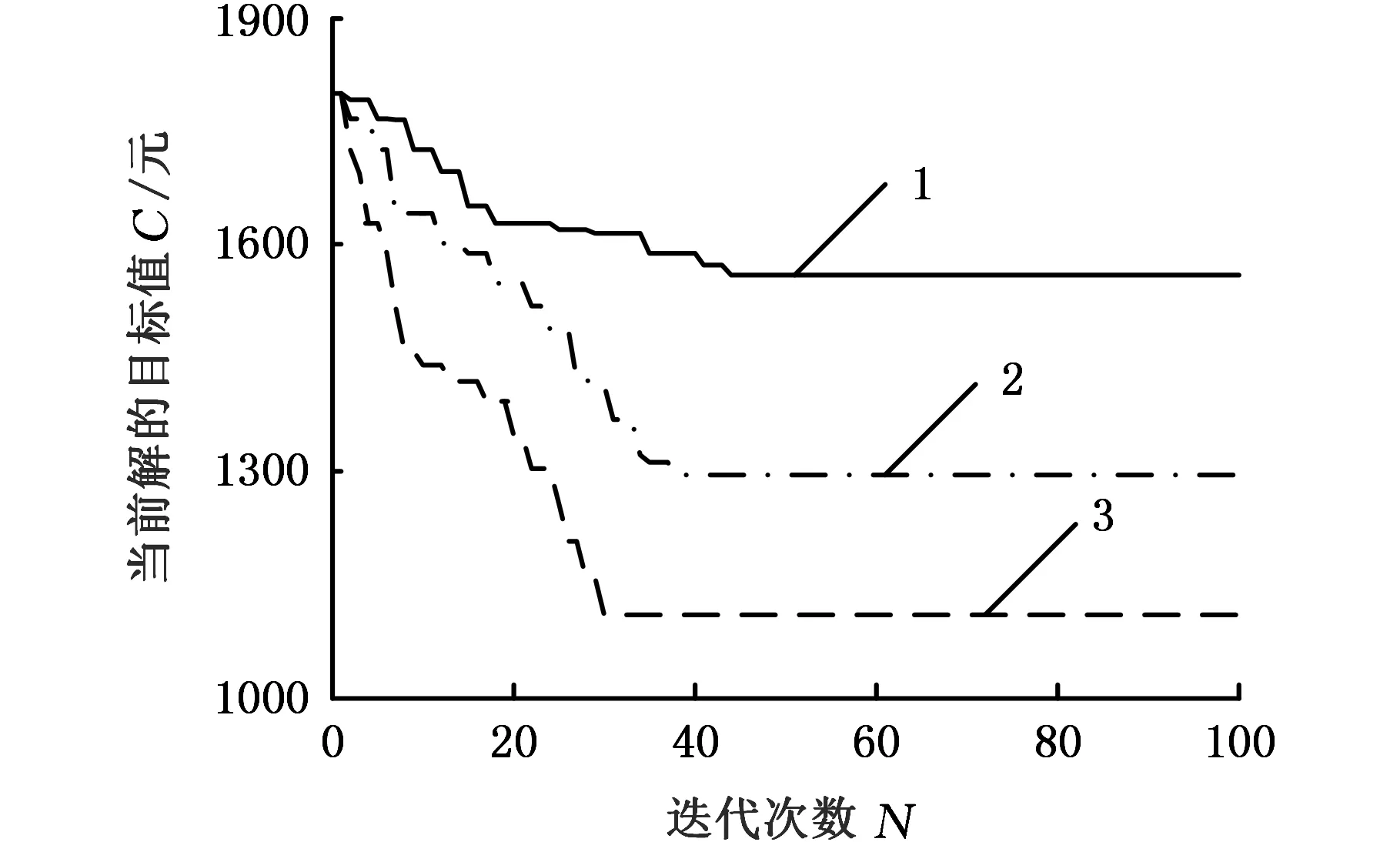
1.传统时间窗 2.三角模糊时间窗 3.正态模糊时间窗图6 三种方法收敛性对比Fig.6 Convergence comparison of three methods

由图6可以得到，正态模糊数方法经过30次迭代收敛，总配送费用为1109.6元。三角模糊数方法经过38次迭代收敛，总配送费用为1294.8元。传统时间窗方法经过44次迭代收敛，总配送费用为1560元。

正态模糊数方法输出最优解染色体为152716311081941，解码后可得到图7所示的配送路径方案：①第2种类型车辆1路线,配送中心1→工位5→工位2→工位7→配送中心1;②第1种类型车辆1路线,配送中心1→工位6→工位3→配送中心1;③第2种类型车辆2路线,配送中心1→工位10→工位8→配送中心1;④第1种类型车辆2路线,配送中心1→工位9→工位4→配送中心1。该路径方案中，同种类型的车辆路线可以互换，经计算该路径方案的总配送路程为11.29 km，总配送时间为234.2 min。

图7 正态模糊数方法配送路径Fig.7 Delivery path of normal fuzzy number method

三角模糊数方法输出最优解染色体为152163110841971，解码后可得到图8所示的配送路径方案：①第2种类型车辆1路线,配送中心1→工位5→工位2→配送中心1;②第1种类型车辆1路线,配送中心1→工位6→工位3→配送中心1;③第2种类型车辆2路线,配送中心1→工位10→工位8→工位4→配送中心1;④第2种类型车辆3路线,配送中心1→工位9→工位7→配送中心1。该路径方案中，同种类型的车辆路线可以互换，经计算该路径方案的总配送路程为12.98 km，总配送时间为262.3 min。

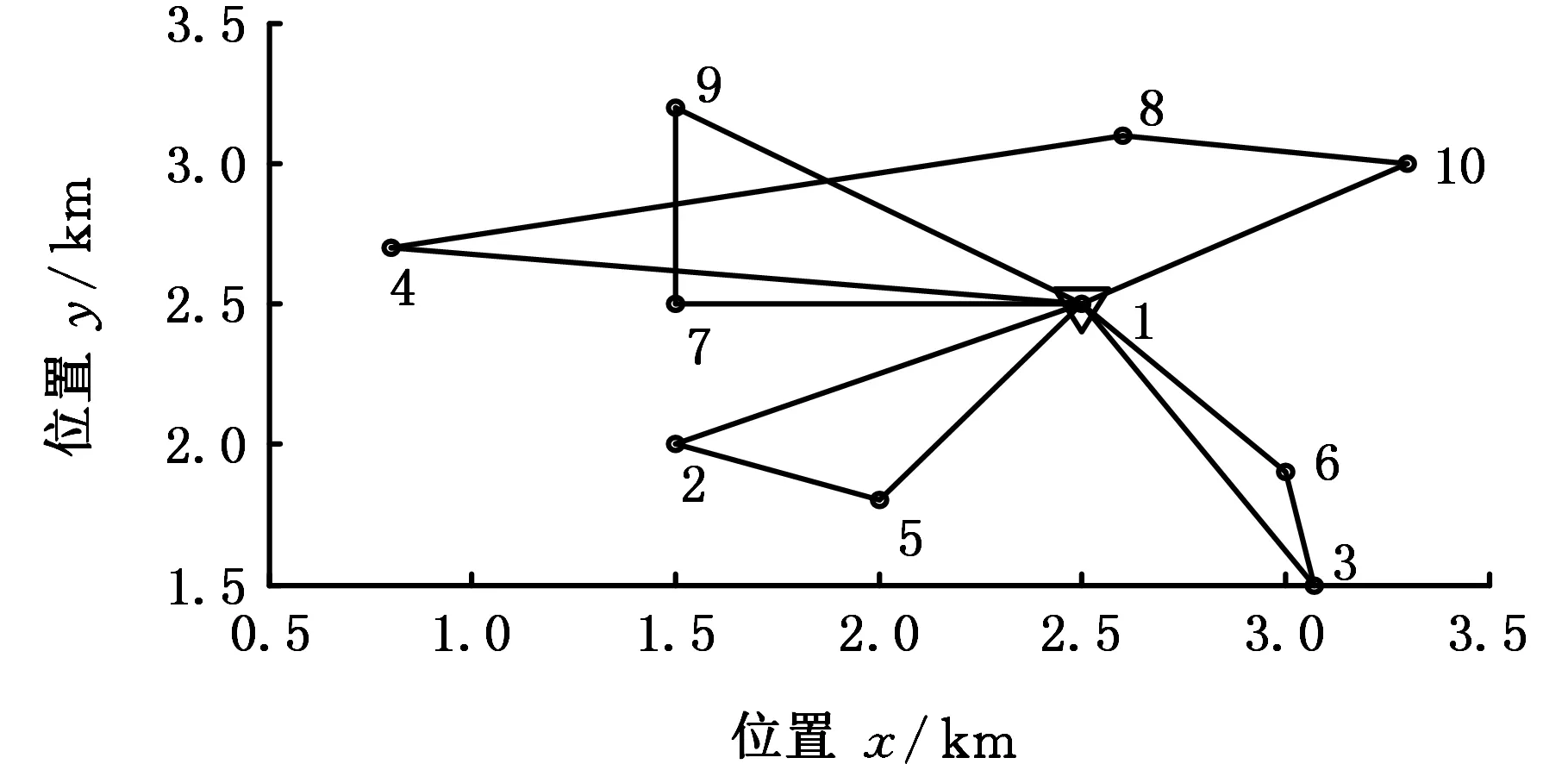
图8 三角模糊数方法配送路径Fig.8 Delivery path of triangular fuzzy number method

传统时间窗方法输出最优解染色体为110851632197141，解码后可得到图9所示的配送路径方案：①第3种类型车辆1路线,配送中心1→工位10→工位8→工位5→配送中心1;②第2种类型车辆1路线,配送中心1→工位6→工位3→工位2→配送中心1;③第2种类型车辆2路线,配送中心1→工位9→工位7→配送中心1;④第1种类型车辆1路线,配送中心1→工位4→配送中心1。该路径方案中，同种类型的车辆路线可以互换，经计算该路径方案的总配送路程为14.24 km，总配送时间为283.3 min。

图9 传统时间窗方法配送路径Fig.9 Delivery path of traditional time window method

从以上仿真结果及其分析可以看出，选取置信度α=0.2时，配送车辆到达工位的时间可选择范围较大，找到目标函数最优解的可能性也较大。与三角模糊数方法相比，正态模糊数方法的收敛速度、总配送费用、总配送路程以及总配送时间均更优；总配送费用减少了16.7%，总配送里程减少了15%，总配送时间缩短了12%。与传统时间窗方法相比，总配送费用减少了40.6%，总配送里程减少了26.1%，总配送时间缩短了21%。

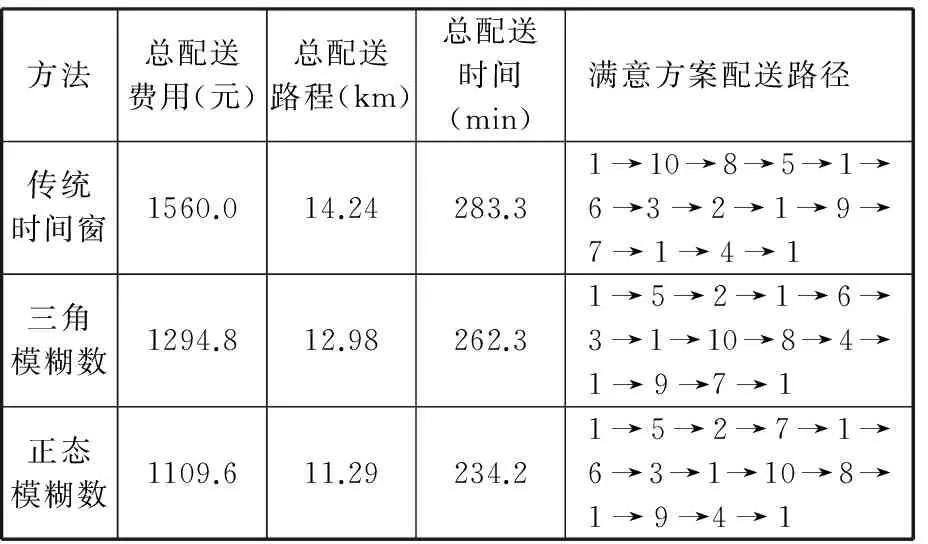
表5 三种方法求解结果对比

5 结语

针对飞机装配生产节拍波动所引起的物料需求时间模糊现象，提出了基于正态模糊时间窗约束的飞机装配物料配送路径规划。采用正态模糊数表征工位物料需求时间参数，其模糊数的隶属度表征工位满意度。以总配送费用最少为目标，建立了带有正态模糊时间窗约束条件的数学模型，为复杂产品物料配送路径规划提供了解决方案。

工程应用实例研究表明：当置信度取值相同时，采用正态模糊数表征工位物料需求时间参数降低了配送费用，提高了物料配送的时效性和准确性。随着置信度的增大，配送车辆到达工位的时间可选择范围将减小，不利于配送路径的优化。选取置信度α=0.2时，与三角模糊数方法和传统时间窗方法相比，正态模糊数方法拥有较好的经济效益和配送效率。

[1] CHENG R, GEN M. Vehicle Routing Problem with Fuzzy Due-time Using Genetic Algorithms[J]. Japanese Journal of Fuzzy Theory and Systems, 1995, 7(5): 1050-1061.

[2] LI Y, GEN M, IDA K. Solving Fuzzy Shortest Path Problems by Neural Networks[J]. Computers & Industrial Engineering, 1996, 31:861-865.

[3] ALI E. New Method for Solving Fuzzy Transportation Problems with LR Flat Fuzzy Numbers[J]. Information Sciences, 2016, 357 (8):108-124.

[4] 张建勇, 李军. 具有模糊旅行时间的VRP的一种混合遗传算法[J]. 管理工程学报, 2006, 20(4): 13-16.

ZHANG Jianyong, LI Jun. A Hybrid Genetic Algorithm to the Vehicle Routing Problem with Fuzzy Traveling Time[J]. Journal of Industrial Engineering and Engineering Management, 2006, 20(4): 13-16.

[5] 李晋航, 黄刚, 贾艳. 多模糊信息条件下的物料配送路径规划问题研究[J]. 机械工程学报, 2011, 47(1): 124-131.

LI Jinhang, HUANG Gang, JIA Yan. Vehicle Routing Problem in Material Distribution under Condition[J]. Journal of Mechanical Engineering, 2011, 47(1):124-131.

[6] 朱晓锋, 蔡延光. 带时间窗的模糊需求多类型车辆路径问题禁忌搜索算法[J]. 广东工业大学学报, 2008, 25(3): 55-60.

ZHU Xiaofeng, CAI Yanguang. Research on Multi-vehicle Scheduling Problems with Fuzzy Demand and Time Windows[J]. Journal of Guangdong University of Technology, 2008, 25(3): 55-60.

[7] 陈钢铁，帅斌. 基于模糊网络和时间依赖的应急车辆调度优化研究[J]. 中国安全科学学报, 2011, 21(8): 171-176.

CHEN Gangtie, SHUAI Bin. Scheduling Optimization of Emergency Vehicle Based on Fuzzy Network and Time-dependent[J]. China Safety Science Journal, 2011, 21(8): 171-176.

[8] 杨翔, 范厚明, 张晓楠, 等. 基于模糊时间窗的多中心开放式车辆路径问题[J]. 计算机集成制造系统, 2016, 22(7): 1768-1778.

YANG Xiang, FAN Houming, ZHANG Xiaonan, et al. Optimization of Multi-deport Open Vehicle Routing Problem with Fuzzy Time Window[J]. Computer Integrated Manufacturing Systems, 2016, 22(7): 1768-1778.

[9] 严正锋, 梅发东, 葛茂根, 等. 基于模糊软时间窗的车间物料流路径优化方法[J]. 计算机集成制造系统, 2015, 21(10): 2760-2767.

YAN Zhengfeng, MEI Fadong, GE Maogen, et al. Path Optimization Method of Workshop Logistics Based on Fuzzy Soft Time Windows[J]. Computer Integrated Manufacturing Systems, 2015, 21(10): 2760-2767.

[10] 王旭坪, 张凯, 胡祥培. 基于模糊时间窗的车辆调度问题研究[J]. 管理工程学报, 2011, 25(3): 148-154.

WANG Xuping, ZHANG Kai, HU Xiangpei. Research of Vehicle Routing Problem Based on Fuzzy Time Windows[J]. Journal of Industrial Engineering and Engineering Management, 2011, 25(3): 148-154.

[11] 马磊磊, 王强. 基于改进遗传算法的多目标物料配送方法研究[J]. 组合机床与自动化加工技术,2015,12(12): 156-160.

MA Leilei, WANG Qiang. Research on Multi-objective Material Delivery Method Based on Improved Genetic Algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015, 12(12): 156-160.

[12] 范玉青. 现代飞机制造技术[M]. 北京:北京航空航天大学出版社, 2001.

FAN Yuqing. Modern Aircraft Manufacturing Technology[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2001.

[13] 《航空制造工程手册》总编委会.航空制造工程手册—飞机装配[M].北京:航空工业出版社,1993.

Chief Compiling Committee of Aeronautic Manufacturing Engineering Manual. Aeronautic Manufacturing Engineering Manual: Aircraft Assembly [M]. Beijing: Aviation Industry Press, 1993.

[14] LUR F, SUNDARAM S. Manufacturing Process Modeling of Boeing 747 Moving Line Concepts[J]. Proceedings of the 2002 Winter Simulation Conference, 2002(1): 1041-1045.

[15] ZHU Wenhua, HAN Hu, FANG Minglun, et al. Studies on Visual Scene Process System of Aircraft Assembly[J]. Journal of Manufacturing Systems, 2013, 32(4): 580-597.

[16] 谢季坚, 刘承平. 模糊数学方法及其应用 [M]. 3版. 武汉:华中科技大学出版社,2006.

Xie Jijian, Liu Chengping.Fuzzy Mathematics Method and Its Application [M]. 3rd ed. Wuhan: Huazhong University of Science and Technology Press, 2006.

AircraftAssemblyMaterialDeliveryPathPlanningBasedonNormalFuzzyTimeWindowConstraints

ZHU Yongguo1LI Junjie2LIU Chunfeng3SONG Likang4

1.School of Aviation Manufacturing Engineering, Nanchang Hangkong University,Nanchang，330063 2.School of Information Engineering,Nanchang Hangkong University,Nanchang，330063 3.The First Component Assembly Factory,Jiangxi Hongdu Aviation Industry Group Limited Liability Company,Nanchang，330024 4.Manager Department,Jiangxi Hongdu Aviation Industry Group Limited Liability Company,Nanchang，330024

Required time of assembly position material requirements was fuzzy during aircraft assembly. A time parameterization method for work station material demands was proposed based on normal fuzzy time window constraints. The membership degree of normal fuzzy numbers was used to represent the satisfaction of stations. Based on the presented normal fuzzy time window constraints, a mathematical model of path planning was established for aircraft assembly material delivery. The presented mathematical model was solved by genetic algorithm. During solution, roulette and best reservation strategy were used as selection operator. Niche selection mechanism of double selection crossover strategy was used as crossover operator, and mutation operator was used to achieve better solutions. MATLAB simulation results show that the presented path planning method has better economic performance.

aircraft assembly; material delivery; normal fuzzy number; path planning

V262.4

10.3969/j.issn.1004-132X.2017.21.003

2016-11-10

国家自然科学基金资助项目(51565042)；江西省重点研发计划资助项目(20161BBE53005,20171BBE50007)

(编辑张洋)

朱永国，男，1978年生。南昌航空大学航空制造工程学院讲师。主要研究方向为飞机数字化装配、装配质量控制等。发表论文20余篇。E-mail:zhuyongguo_2003@163.com。李俊杰，男，1990年生。南昌航空大学信息工程学院硕士研究生。刘春锋，男，1983年生。江西洪都航空工业集团有限责任公司高级工程师。宋利康，男，1960年生。江西洪都航空工业集团有限责任公司研究员级高级工程师。