基于Stribeck摩擦模型的盘式摩擦副稳定性分析

王延忠 郭 超 贾树王 宁克焱 兰 海

1.北京航空航天大学机械工程学院，北京，1001912.中国北方车辆研究所，北京，100072

基于Stribeck摩擦模型的盘式摩擦副稳定性分析

王延忠1郭 超1贾树王1宁克焱2兰 海2

1.北京航空航天大学机械工程学院，北京，1001912.中国北方车辆研究所，北京，100072

为了分析摩擦副滑动摩擦状态下的稳定性，分析系统的失稳条件，以Stribeck摩擦模型为基础，建立了速度相关的多自由度摩擦副滑动稳定性分析模型。建立了盘式摩擦副的系统动力学微分方程，进行了基于库仑摩擦定律摩擦力计算公式的级数展开，随后依据李雅普诺夫稳定性判据进行了系统稳定性求解，并分析了系统关键参数对系统稳定性的影响。研究结果表明，采用减小Stribeck系数和摩擦因数静动比、减小外载荷和增大系统阻尼等方法，能提高系统的稳定性。

盘式摩擦副；稳定性；Stribeck摩擦模型；动力学方程

0 引言

制动器振动失稳问题一直是制动器设计中亟待解决的问题。因振动失稳而产生的制动器啸叫不仅影响制动器寿命，也影响制动平稳性。20世纪初，Stribeck通过对径向滑动轴承的研究提出了著名的Stribeck曲线[1]。1931年JACOBSEN[2]和DENHARTOG[3]建立了微分方程来描述单自由度系统的黏滑运动。20世纪50年代起，不少学者针对摩擦引起振动的现象以及滑动摩擦的动力学特征等问题进行了研究[4]。制动器发出尖锐刺耳的高频噪声的主要原因是摩擦片和对偶片相对摩擦。MARTINS等[5]将摩擦引起的振动归纳为两类，即黏滑模式和准简谐模式，发生的条件在于不同的表面滑动速度。BLOK[6]发现，阻尼的增加能有效减弱黏滑现象，发生摩擦振荡的基本条件是在减小摩擦力的同时，增大滑动速度。TOLSTOI[7]和KO等[8]也发现，振动现象是由相对滑动速度和摩擦因数的变化引起的。马建敏等[9]建立了非旋转体在摩擦力作用下的振动方程，并研究了其运动规律。学者们建立的理论和计算过程虽有差别，但是其研究的焦点却是相同的，即振动产生的源头——摩擦片和对偶片的相对转动。

虽然前人进行了大量的摩擦振动失稳研究，但是到目前为止，由摩擦引起的振动失稳现象仍然难以完全被解释清楚，主要原因如下：摩擦过程是典型的非线性系统，所涉及的参数复杂性较高，参数之间相互影响；摩擦现象不仅涉及表面接触状态，也与润滑和工况有关。各种因素相互影响，干扰了研究人员的分析。本文从系统建模入手，建立了符合Stribeck摩擦特性的系统动力学方程，将与摩擦相关的各项因素用摩擦特性曲线的形式表示，再对统一的摩擦特性进行系统稳定性分析，简化了分析方法，从而通过稳定性判据对系统的主要参数——外载荷、阻尼和特征速度等进行了分析。

1 盘式摩擦副结构动力学模型

摩擦副失稳现象的本质是系统受到微小扰动之后出现的系统振动不收敛问题。对于高频振动、啸叫与系统失稳成因，公认的是系统中的不稳定性。造成扰动的因素很多，主要有以下几方面：圆周方向的厚度波动；轴向摆动；摩擦因数变化；相对速度变化；摩擦副的刚度、阻尼；摩擦与耦合条件等。为了探明各因素对摩擦副振动失稳的影响程度，需要针对盘式摩擦副结构建立动力学模型。

1.1摩擦副系统

由于轴向载荷对摩擦副振动影响较大[7]，本文建立的动力学模型不仅包含摩擦副旋转方向的自由度，也包含摩擦副轴向的自由度。如图1所示，摩擦片旋转，对偶片与机架固定，由于装配关系的存在，对偶片与支架之间存在接触关系。加载力Fapp沿轴向施加，设定沿加载力方向的位移为x1，摩擦副的半径为R，摩擦片的转角为θ，摩擦片及其附属结构质量为m1，转动惯量为I，k1、k2、k3为系统刚度，FR为摩擦力。

图1 摩擦副结构的系统动力学模型Fig.1 System dynamics model of friction structure

在摩擦副的周向，m2代表对偶片质量，在相对滑动的瞬间，对偶片一方面受到摩擦片的切向摩擦力，另一方面对支架施加周向力。m2切向方向的位移设定为x2，摩擦片的角速度为ω。

1.2动力学微分方程

系统的动力学微分方程的建立有多种方法，本文采用的是Lagrange系统建模法。Lagrange第二类方程的一般形式为

(1)

根据图1的动力学模型，系统动能T、系统势能V分别为

(2)

(3)

将式(2)求偏导数，得

(4)

系统动能中不含广义坐标，所以求得

(5)

将式(3)对广义坐标进行求导得

(6)

与广义坐标相对应的广义力

(7)

将式(4)～式(7)代入式(1)，则系统的动力学微分方程表示为

(8)

2 基于Stribeck模型的摩擦稳定性计算

2.1Stribeck模型

根据Stribeck效应所对应表达形式的差异，Stribeck模型通常可分为Tustin模型、Gauss模型和Lorente模型[10]。本文采用Gauss模型，其数学表达式为

f(v)=μk+(μs-μk)e-(v/vs)2+σv

(9)

式中，f(v)为Stribeck摩擦因数；μk为库仑模型的滑动摩擦因数；μs为摩擦副的最大静摩擦因数；v为摩擦副的相对滑动速度；vs为Stribeck系数，也称Stribeck速度；σ为黏性系数。

对式(9)进行求导，获得一阶导数公式：

(10)

一般来说，对于相同材料，μk和μs是常量。Stribeck模型描述了摩擦副摩擦因数的变化，其主要影响参数为Stribeck系数vs，图2所示为不同vs下的Stribeck曲线和Stribeck求导曲线。vs越大，摩擦因数的极小值越大，摩擦因数的变化范围越小。由图2可见，如果线速度从50 m/s下降到0(即制动减速过程)，则摩擦因数的变化是非常大的，速度曲线的非线性变化带来冲击，所以符合Stribeck摩擦特性的材料在低速滑动过程中更容易出现振动失稳现象。

(a)Stribeck曲线

(b)Stribeck求导曲线图2 不同vs下的Stribeck曲线和Stribeck求导曲线Fig.2 Stribeck curves and curves of Stribeck derivative under different vs

2.2模型稳定性求解

根据库仑定理，摩擦力

FR=x1k2f(vr)

对FR在(x10,vr=0)进行二元泰勒级数展开，可得

(11)

将式(9)代入式(11)后，就可以计算出摩擦力FR，然后将式(11) 代入式(8)后，获得考虑Stribeck摩擦模型的系统动力学方程：

(12)

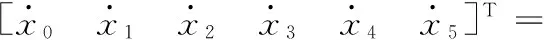
则系统矩阵

(13)

由稳定性判定定理得：在一次近似的基础上，系数矩阵A的特征值都具有负实部，则原非线性系统在平衡点是渐进稳定的，而且系统的稳定性与高阶部分R(v)无关，所以通过判定矩阵A特征值实部的正负就可以判定非线性系统的稳定性。

2.3计算实例

通过代入参数，可以计算出矩阵的特征值。参数列表见表1。

通过计算获取了不同速度下特征值实部的曲线分布，如图3a所示。由于二阶数值相比一阶、三阶更大，所以单独绘制了一阶、三阶曲线，如图3b所示。可见在较高速度下，系统的所有特征值Reω<0，说明系统渐进稳定；但是在较低线速度下，系统呈现不稳定状态。由于一阶、二阶特征值的变化趋势相同，但是系统扰动对二阶特征值的影响程度更高，故本文重点探究各项参数对二阶特征值的影响。

(a)特征值实部一阶、二阶、三阶曲线

(b)特征值实部一阶、三阶曲线图3 特征值实部曲线Fig.3 Thereal part curves of eigenvalues

3 计算结果分析

由于稳定性的影响因素众多，本文进行典型参数的影响性分析。分别获得外载荷Fapp、阻尼c、Stribeck系数vs和摩擦因数(μk和μs)对系统稳定性的影响。

图4所示为外载荷对系统稳定性的影响，随着载荷的增大，系统不稳定趋势增大，但是系统进入稳定状态的线速度变化不大。对比图5a和图5b，系统阻尼c3的变化对一阶特征值实部和二阶特征值实部的影响趋势总体相同，但是对一阶特征值影响很小，二阶特征值的影响相对较大。如图6所示，c1对系统的一阶特征值实部的影响趋势与c3相同，一般来说，c3与制动器的支撑结构有关，c1与摩擦材料特性有关。阻尼的增大有助于提高系统稳定性，所以在制动器摩擦稳定性设计中，应该尽量选择阻尼较大的摩擦材料。比如目前对于车辆摩擦片，纸基材料有替代粉末冶金材料的趋势，就是由于纸基材料摩擦稳定性更好。

图4 外载荷对二阶特征值实部的影响Fig.4 Effect of external load on the 2nd eigenvalue

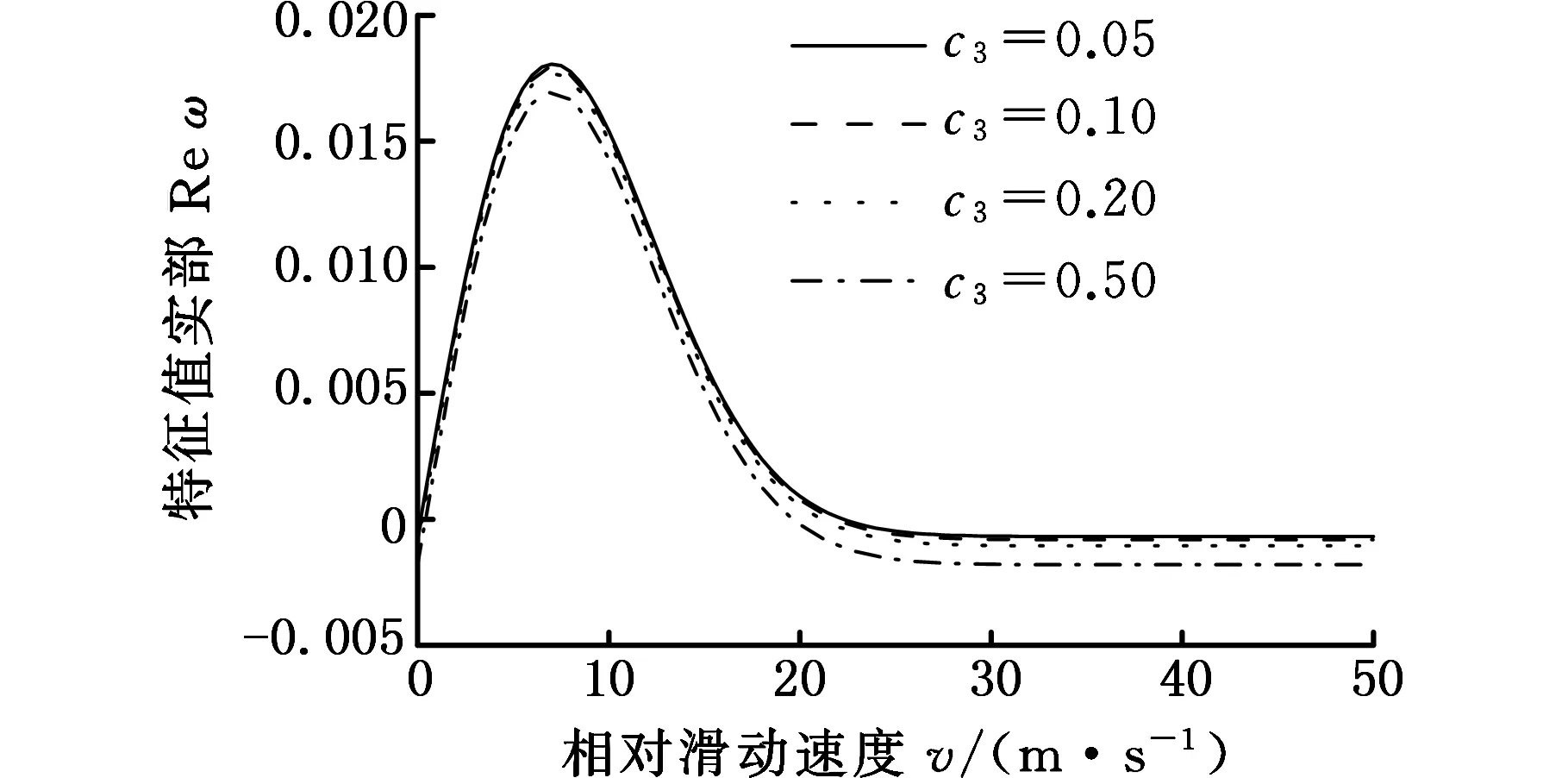
(a)一阶特征值

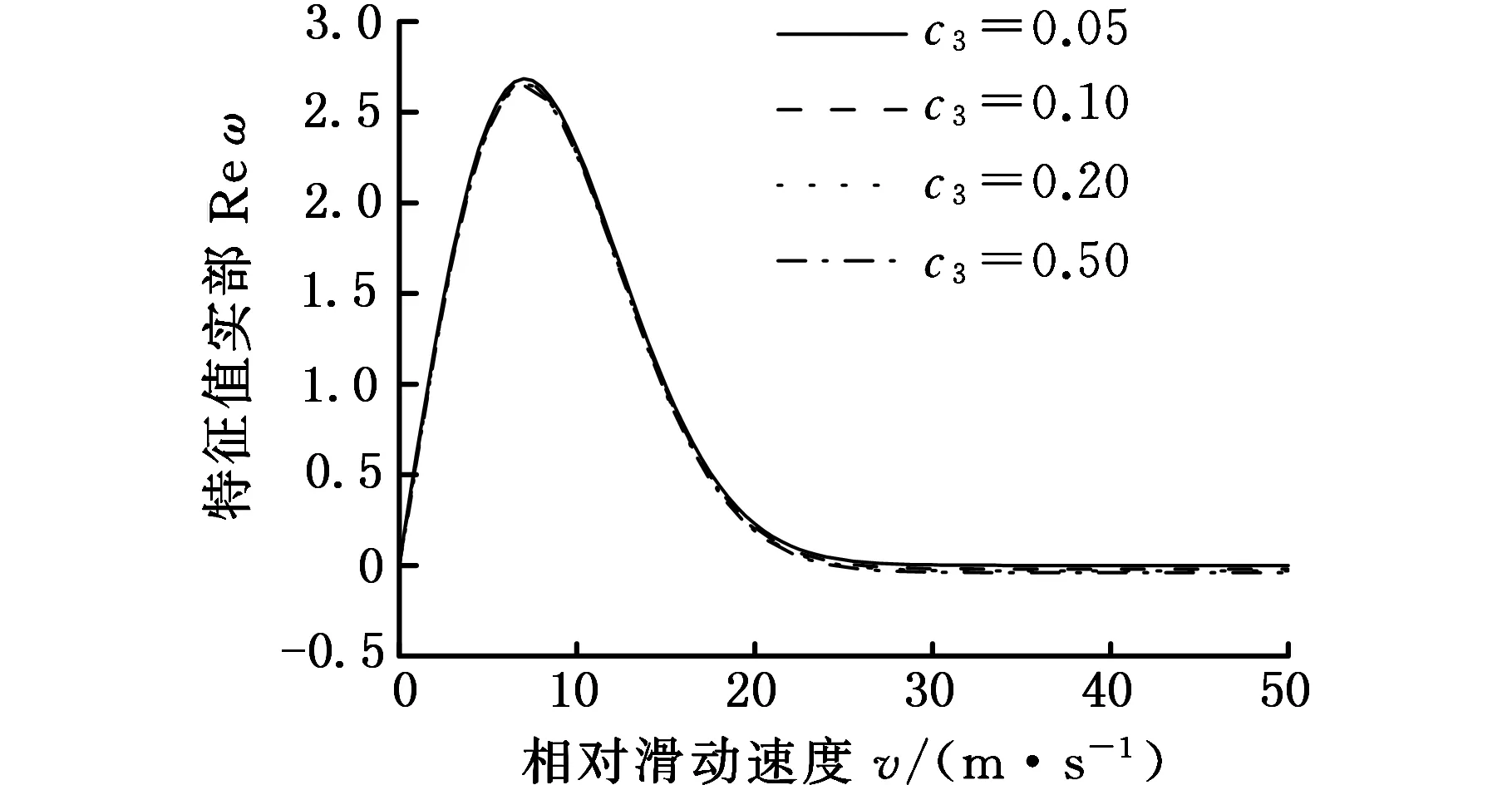
(b)二阶特征值图5 系统阻尼c3对特征值实部的影响Fig.5 Effect of the system damping c3 on the eigenvalue

图6 系统阻尼c1对一阶特征值实部的影响Fig.6 Effect of the system damping c1 on the first order eigenvalue

虽然外载荷对系统稳定的影响也较强，但是在实际工程应用中外载荷往往有指标要求，难以随意降低或者更改，所以系统的摩擦特性对于系统的稳定性影响起决定作用。图7a所示为不同的Stribeck系数vs对二阶特征值实部曲线的影响，随着vs值的减小，系统的扰动增强，但是系统却能更快地进入稳定状态，系统的稳定区间大大增加。图7b所示为系统摩擦因数静动比μs/μk对特征值的影响，随着静动比的增大，系统不稳定程度增大。对于制动器而言，提高Stribeck系数vs是较为复杂的过程，这与摩擦副接触状态和润滑状态等有关。通过改善摩擦副接触状态、润滑状态等边界条件，从而优化系统的摩擦因数曲线，可以有效增强系统的稳定程度。相比而言，降低系统的静动比更为简单，动摩擦因数对制动器设计来说一般越大越好，较大的动摩擦因数可以提高摩擦扭矩，使车辆更快地停下来，但是较大的摩擦因数也会带来材料磨损严重的问题。

(a)Stribeck系数对二阶特征值的影响

(b)不同静动比对二阶特征值的影响图7 Stribeck系数和不同静动比对二阶特征值的影响Fig.7 Effect of Stribeck coefficient and the dynamic to static rat on the 2nd eigenvalue

4 结论

(1)盘式摩擦副在线速度较低时系统呈现不稳定状态，随着线速度的提高，系统渐进进入稳定状态。

(2)三阶特征值实部恒为负值，一阶和二阶特征值实部对系统稳定性起决定作用，其中，二阶特征值影响程度更大。

(3)减小Stribeck系数和摩擦因数静动比，减小外载荷和增大系统阻尼，均能提高系统稳定性，其中，减小vs和降低摩擦因数静动比最为有效。

[1] DOWSON D. History of Tribology[M]. London:Longmans,1979.

[2] JOBCOBSEN L S. Steady Forced Vibration as Influenced by Damping[J]. Trans. of the ASME,1931,53:169-181.

[3] DENHARTOG J P. Forced Vibration with Combined Coulomb and Viscous Friction[J]. Trans. of the ASME,1931,52:107-115.

[4] KO P L. Autonomous Quasi-harmonic and Forced Vibration of Frictional System[D].Vancouver:University of British Columbia,1969.

[5] MARTINS J A C, ODEN J T,SIMOES F M F. A Study of Static and Kinetic Friction[J]. International Journal of Engine Science,1990,28(1):29-92.

[6] BLOK H. Fundamental Aspects of Boundary Lubrication[J]. Journal SOC Automotive Engineerings,1940:46-54.

[7] TOLSTOI D. Signiticance of the Normal Degree of Freedom and Natural Vibrations in Contact Friction[J]. Wear,1984,102:193-213.

[8] KO P L,TAPONAT M C， PFAIFER R.Friction-induced Vibration-with and without External Disturbance[J]. Tribology international,2001,34(1):7-24.

[9] 马建敏,黄协清,陈天宁.旋转与非旋转体间接接触摩擦诱发振动的理论分析[J].西安交通大学学报,1999,33(1):101-105.

MA Jianmin，HUANG Xieqing，CHEN Tianning. Contact Friction Induced Vibration between Revolute and Non-revolute Bodies[J].Journal of Xi’an Jiaotong University,1999,33(1):101-105.

[10] 林朝安.基于能量法则的Stribeck摩擦模型参数辨识及其应用研究[D].南宁：广西大学, 2015.

LIN Chaoan. Parameter Identification of Stribeck Friction Model Based on Energy Principle and Its Application[D]. Nanning：Guangxi University, 2015.

StabilityAnalysisofDiscFrictionPairsBasedonStribeckModel

WANG Yanzhong1GUO Chao1JIA Shuwang1NING Keyan2LAN Hai2

1.School of Mechanical Engineering, Beijing University of Aeronautics and Astronautics,Beijing,100191 2.National Key Lab. of Vehicular Transmission, China North Vehicle Research Institute,Beijing,100072

In order to obtain system stability of friction pairs under sliding and analyze instability of the system, a multiple-degree-of-freedom and velocity-related sliding stability analysis model was established based on Stribeck friction model herein. The dynamics differential equations were established for the disc-friction pairs and the Coulomb friction formula was expanded with Taylor method. Then the system stability and the effects of key parameters on the system characteristics were analyzed depending on Liapunov’s stability criterion. The results show that the system stability may be intensified by decreasing Stribeck coefficient, ratio of static friction and sliding friction and load, or increasing the system damping etc.

disc friction pair; stability; Stribeck friction model; dynamics equation

TH117

10.3969/j.issn.1004-132X.2017.21.001

2016-12-14

国家自然科学基金资助项目(51275020)；基础产品创新科研计划资助项目(20146404)

(编辑陈勇)

王延忠，男，1963年生。北京航空航天大学机械工程学院教授、博士研究生导师。主要研究方向为精密传动技术及精密齿轮制造。发表论文100余篇。郭超(通信作者)，男，1986年生。北京航空航天大学机械工程学院博士研究生。E-mail:buaaguochao@163.com。贾树王，男，1992年生。北京航空航天大学机械工程学院硕士研究生。宁克焱，男，1974年生。中国北方车辆研究所研究员。兰海，男，1983年生。中国北方车辆研究所高级工程师。