基于数值模拟和回归正交设计的AA5754铝合金温成形回弹特性

申国哲，葛永鹏，刘立忠，赵坤民



基于数值模拟和回归正交设计的AA5754铝合金温成形回弹特性

申国哲1, 2，葛永鹏2，刘立忠3，赵坤民1, 2

(1. 大连理工大学工业装备结构分析国家重点实验室，辽宁大连，116024；2. 大连理工大学汽车工程学院，辽宁大连，116024；3. 东北大学材料科学与工程学院，辽宁沈阳，110819)

以圆筒温拉深切环实验为基础，采用数值模拟与回归正交试验相结合的方法，建立铝合金温成形过程中板料成形初始温度、摩擦因数、压边力、凹模圆角半径和凸凹模间隙与回弹之间的回归模型，得出各工艺参数对制件回弹的影响规律，确定最优工艺参数组合。通过回归模型进行回弹预测，并与相同工艺条件下4种温度的实验结果和数值模拟结果进行比较。研究结果表明：回归模型显著性明显，拟合度高，预测结果具有较高的可信度。

数值模拟；回归正交试验；铝合金；温成形；回弹；回归模型

铝合金板具有密度小、比强度高、耐腐蚀性强等优点，成为目前替代汽车用钢板的主要轻量化材 料[1−3]。但它在室温条件下塑性低，成形性能差，直接影响到制件的形状和尺寸精度。铝合金的温成形工艺因其能显著提高板料塑性、明显改善回弹现象从而受到国内外研究者的广泛关注。ABEDRABBO等[4]进行了不同温度、不同应变速率下的铝合金温成形实验，建立了与温度和应变速率相关的各向异性材料模型。王孟君等[5]采用差温拉伸实验，得出了铝合金温拉伸时的流变行为以及极限拉伸比随变形温度、拉伸速率和压边力的变化规律。铝合金温成形的趋势是精密成形，然而，针对其在温成形工艺条件下的回弹研究目前还很少涉及，大多数处于简单的弯曲变形研究 上[6]。为此，本文作者以GRÈZE等[7]的铝合金圆筒温拉深切环实验为基础，采用数值模拟与回归正交试验相结合的方法，研究板料成形初始温度、摩擦因数、压边力、凹模圆角半径和凸凹模间隙对制件回弹的影响，建立温成形工艺中铝合金制件回弹的多元回归模型，揭示其回弹规律。

1 实验方法的确定

回归正交设计是正交试验设计和回归分析的有机结合，不仅有合理的试验设计和较少的试验次数，而且能建立有效的数学模型。它可以在因素的试验范围内选择适当的试验点，用较少的试验建立1个精度高、统计性质好的回归方程，并能解决试验优化问题，广泛应用于实际生产和科学试验[8−10]。由于试验涉及的影响因素较多，本文采用一次回归正交试验的方法进行分析，试验设计流程如图1所示。建立试验指标与个因素1, x, …,x之间的一次回归数学模型：

2 有限元模型的建立与实验结果验证

2.1 有限元模型的建立

以 GRÈZE等[7]提出的圆筒温拉深切环实验为基础，利用板料冲压成形仿真软件Dynaform对实验过程进行数值模拟。圆筒拉深具有轴对称性，为提高计算效率，取板料的1/2建立有限元模型，温成形有限元模型如图2所示。其中板料为弹塑性变形体，凸凹模及压边圈为刚性体，板料单元采用全积分壳单元。

图1 回归正交试验设计流程图

图2 温成形有限元模型

铝合金材料的本构模型采用3参数Barlat-Lian厚向异性屈服准则[11−14]。数值模拟需要设定热边界条件，本模型的热边界条件是设置模具温度，使凸模、凹模和压边圈的温度在温成形过程中保持恒定，始终与板料的成形初始温度相等。在拉深过程中，板料在塑性变形的同时发生动态回复，温度发生变化，从而与模具发生热交换。模拟热交换需要定义热接触条件，通常用热传递系数来定义，本模型根据模具和板料的间隙来定义可变的热传递系数。为简化计算，当模具与板料距离小于0.5 mm时，热传递系数设为5 500 W/(m2∙℃)[15]；当模具与板料的距离超过0.5 mm时，认为模具与板料之间无热传递发生。数值模拟过程与实验过程一致，分为成形、空冷、切割和回弹4步，模拟流程如图3所示。

图3 数值模拟流程

2.2 实验结果验证

引用GRÈZE等[7]的圆筒温拉深切环实验，取其实验结果及数值模拟结果与本文在相同工艺条件下所得回弹量数值模拟结果进行比较，如表1所示。

从表1可以看出：本文回弹量数值模拟中回弹的计算精度要远远高于GRÈZE等[7]的计算精度。这是因为GRÈZE等[7]在数值模拟中采用的单元类型为三维实体单元，而体单元在板料成形模拟中存在缺陷。为了平衡计算精度与计算效率的影响效应，体单元的长宽比相对较大，导致板料网格质量较差，回弹量数值模拟精度降低。而本文数值模拟中采用的壳单元则不存在上述缺陷，因此，回弹量计算精度较高。同时，壳单元在板料成形数值模拟中的优越性也得到了进一步体现。此外，本文回弹量数值模拟结果与实验结果较接近，说明数值模拟结果可靠，并且所建立的有限元模型正确，为后续数值模拟结果的正确性提供了保证。

表1 实验与数值模拟结果

注：为本文回弹量模拟值与实验值之间的相对误差；′为GRÈZE等[8]的回弹量模拟值与实验值之间的相对误差。

3 回归模型的建立和检验

3.1 回归模型的建立

影响制件回弹的工艺参数很多，本文针对影响回弹的显著性水平，选用板料成形初始温度、摩擦因数、压边力、凹模圆角半径和凸凹模间隙共5个工艺参数。除温度以外，将GRÈZE等[7]实验中的工艺参数值作为本文数值模拟参数取值范围的中间值，参数取值范围如表2所示。

选取开口圆环张开的直线距离作为回弹量的试验指标，以上述5个工艺参数作为考察因素，并考虑所有因素间的交互作用，应用一次回归正交试验分析这5个因素和试验指标之间的关系。将因素x的各水平进行线性变换，即

表2 工艺参数取值范围

一次回归正交试验设计方案及试验结果如表4所示，其中第17，18和19号试验称为零水平试验或中心试验。进行零水平试验的目的是为了更精确地进行统计分析，得到精度较高的回归模型。每组有限元仿真的方案由z对应的水平确定，其中zz为交互作用项xx对应的编码即0，−1或者1。利用Dynaform进行有限元建模与数值模拟，并记录回弹的仿真结果。

表3 一次回归正交实验因素水平编码

一次回归方程系数的计算公式为：

表4 一次回归正交试验设计方案及实验结果

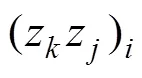
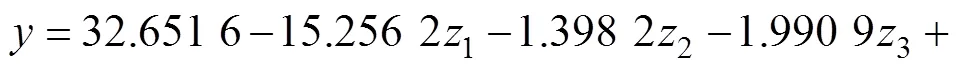
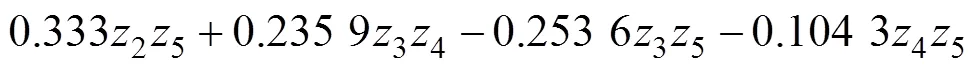
3.2 回归模型的显著性检验

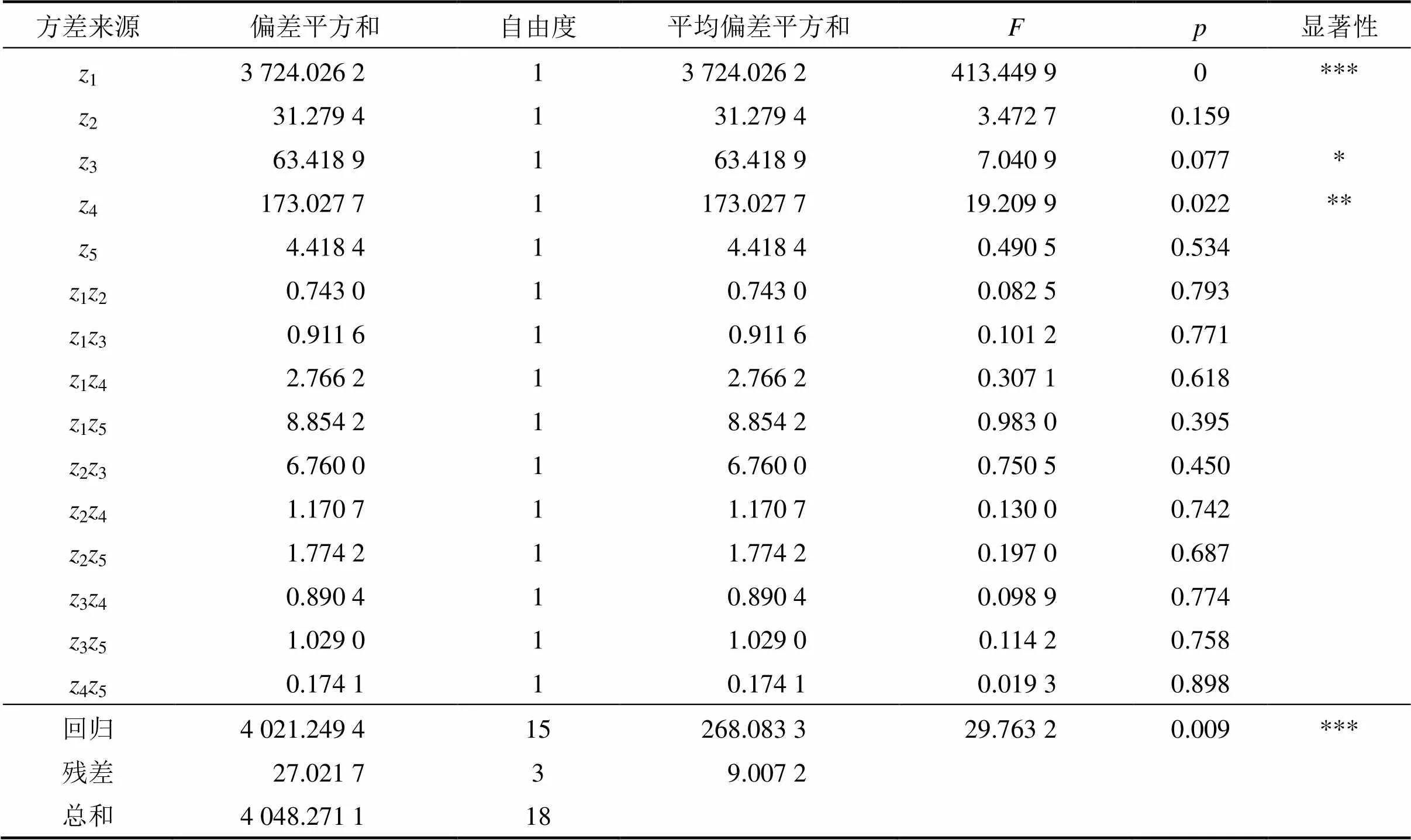
表5 回弹量方差分析结果

注：0.1(1,3)=5.54，0.05(1,3)=10.13，0.01(1,3)=34.12，0.01(15,3)=26.87；形式F0.1(1,3)中，0.1为显著度，1和3为自由度(其余类推)，和为方差分析中的指标，越大，越小，表示结果越可靠，即显著性越高；“*”表示一般显著；“**”表示比较显著；“***”表示非常显著。

表6 第二次方差分析结果

注：0.01(1,14)=8.86，0.01(4,14)=5.04，0.05(1,14)=4.60。

3.3 回归模型的失拟性检验

对回归模型进行失拟性检验，结果如表7所示。从表7可以看出：复相关系数为0.997，接近1.000，且＜0.05(12,2)，说明试验指标与各因素之间存在较好的线性关系，并且所建立的回归模型失拟性不显著，与实际情况拟合程度较高。

表7 回归模型失拟性检验

3.4 回归模型的回代

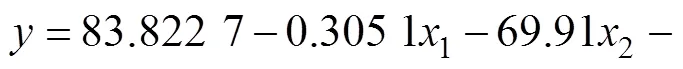
上述回归模型说明工艺参数间的交互作用可以忽略，板料成形初始温度、摩擦因素、压边力和凹模圆角半径对制件回弹均有显著影响，且影响效应具有较好的可加性。根据回归模型，可以得出使回弹量最小的最优工艺参数组合：板料成形初始温度为200 ℃，摩擦因素为0.20，压边力为32 kN，凹模圆角半径为 6 mm。这与通过正交试验得出的结果一致。

3.5 回归模型的验证

将表1所示回弹量实验结果、数值模拟结果分别与相同工艺条件下的回归预测结果进行比较，结果见表8。从表8可以看出：回弹量回归预测结果与实验结果、数值模拟结果较接近，说明本文建立的回归模型可信度高，能准确地反映温成形工艺中铝合金制件回弹量与工艺参数之间的关系。

表8 回弹量回归预测结果与实验结果和数值模拟结果的相对误差

注：1为预测值与实验值之间的相对误差；2为预测值与模拟值之间的相对误差。

为了进一步验证回归模型的可靠性，在数值模拟的基础上，对其涉及的板料成形初始温度、摩擦因素、压边力和凹模圆角半径进行正交试验设计。已知工艺参数间的交互作用可以忽略，选取正交表L9(34)，以模拟回弹量s作为试验指标，将各组模拟结果分别与其对应的回归预测结果进行比较，如表9所示。从表9可见：88.89%的各参数回归预测结果与数值模拟结果的相对误差在10%以内，考虑到任何试验都不可避免地存在试验误差，回归模型的可靠性得到了进一步验证。

表9 回归预测与数值模拟的相对误差

相对于数值模拟，回归预测存在一定的局限性。预测精度对制件形状依赖性较强，若制件形状发生变化，则回归模型也要进行相应修改。然而，在实际应用中，回归预测的方法非常实用。在冲压工艺中，工艺参数对制件质量的影响包括制件回弹和最优工艺参数的确定。若运用数值模拟方法，则只能通过有限元仿真验证工艺设计是否合理。为了确定最优工艺参数，更需要进行大量仿真试验，这存在很大的盲目性。运用回归正交试验设计的方法，为了建立回归模型，仿真试验根据回归正交试验方案进行，可明显减小设计的复杂度和工作量，从而大大减少仿真时间，提高工作效率。通过回归模型，可以快速得出各工艺参数对制件回弹量的影响，为冲压工艺的参数优化设计提供重要依据。此外，也可以在回归正交试验中加入更多的影响因素，使得回归模型愈加完善和精确。

4 结论

1) 在铝合金温成形工艺中，工艺参数间的交互作用可以忽略；板料成形初始温度、摩擦因素、压边力和凹模圆角半径对制件回弹均有显著影响，且影响效应具有较好的可加性。

2) 通过回归模型对制件回弹量进行回归预测，预测结果与相同工艺条件下的实验结果及数值模拟结果较接近，说明本文建立的回归模型可信度高，能准确反映温成形工艺中铝合金制件回弹与工艺参数之间的关系。

3) 在实际应用中，回归模型可以明显减小数值模拟的复杂度和工作量，快速得出各工艺参数对制件回弹的影响规律，为冲压工艺的优化设计提供依据。

[1] HIRSCH J, AL-SAMMAN T. Superior light metals by texture engineering: optimized aluminum and magnesium alloys for automotive applications[J]. Acta Materialia, 2013, 61(3): 818−843.

[2] MAYYAS A, QATTAWI A, OMAR M, et al. Design for sustainability in automotive industry: a comprehensive review[J]. Renewable & Sustainable Energy Reviews, 2012, 16(4): 1845−1862.

[3] HIRSCH J. Aluminum in innovative light-weight car design[J]. Materials Transactions, 2011, 52(5): 818−824.

[4] ABEDRABBO N, POURBOGHRAT F, CARSLEY J. Forming of aluminum alloys at elevated temperatures. Part 1: material characterization[J]. International Journal of Plasticity, 2006, 22(2): 314−341.

[5] 王孟君, 任杰, 黄电源, 等. 汽车用5182铝合金板材的温拉伸流变行为[J]. 中国有色金属学报, 2008, 18(11): 1958−1963. WANG Mengjun, REN Jie, HUANG Dianyuan, et al. Flow behavior of 5182 aluminum alloy for automotive body sheet during warn tensile deformation[J]. Chinese Journal of Nonferrous Metals, 2008, 18(11): 1958−1963.

[6] MOON Y H, KANG S S, CHO J R, et al. Effect of tool temperature on the reduction of the springback of aluminum sheets[J]. Journal of Materials Processing Technology, 2003, 132(1/2/3): 365−368.

[7] GRÈZE R, MANACH P Y, LAURENT H, et al. Influence of the temperature on residual stresses and springback effect in an aluminum alloy[J]. International Journal of Mechanical Sciences, 2010, 52(9): 1094−1100.

[8] WHITCOMB M A P. Design of experiments: statistical principles of research design and analysis[J]. Technometrics, 2012, 43(2): 236−237.

[9] MONTGOMERY D C. Design and analysis of experiments, 8th edition[J]. Environmental Progress & Sustainable Energy, 2013, 32(1): 8−10.

[10] SANTNER T J, WILLIAMS B J, NOTZ W I. The design and analysis of computer experiments[J]. Asta Advances in Statistical Analysis, 2010, 94(4): 307−309.

[11] LIN Zhongqin, WANG Wurong, CHEN Guanlong. A new strategy to optimize variable blank holder force towards improving the forming limits of aluminum sheet metal forming[J]. Journal of Materials Processing Technology, 2007, 183(2/3): 339−346.

[12] YU Zhongqi, LIN Zhongqin, ZHAO Yixi. Evaluation of fracture limit in automotive aluminum alloy sheet forming[J]. Materials and Design, 2007, 17(6): 1169−1174.

[13] BANABIC D, KUWABARA T, BALAN T, et al. Non-quadratic yield criterion for orthotropic sheet metals under plane-stress conditions[J]. International Journal of Mechanical Sciences, 2003, 45(5): 797−811.

[14] 赵茂俞, 薛克敏, 李萍. 多元非线性回归的铝合金覆盖件成形模拟优化设计[J]. 农业机械学报, 2008, 39(9): 166−169. ZHAO Maoyu, XUE Kemin, LI Ping. Numerical simulation and optimization of aluminum alloy auto panel forming by multivariate nonlinear regressing[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(9): 166−169.

[15] LAURENT H, COËR J, MANACH P Y, et al. Experimental and numerical studies on the warm deep drawing of an Al-Mg alloy[J]. International Journal of Mechanical Sciences, 2015, 93: 59−72.

(编辑 陈灿华)

Springback analysis of warm forming for aluminum alloy AA5754 by numerical simulation method in conjunction with regression orthogonal design

SHEN Guozhe1, 2, GE Yongpeng2, LIU Lizhong3, ZHAO Kunmin1, 2

(1. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China;2. School of Automotive Engineering, Dalian University of Technology, Dalian 116024, China;3. School of Material Science and Engineering, Northeastern University, Shenyang 110819, China)

Based on the split-ring experiment for cylindrical drawing cups,a regression model of relationship between springback and process parameters,including initial forming temperature of blank,friction coefficient, blank holder force,die radius and clearance between punch and die,was established for warm forming of aluminum alloyby numerical simulation method in conjunction with the regression orthogonal test.The effect of process parameters on springback was investigated,and the optimal combination of process parameters was determined. The regression model was applied to predict the springback,whose results were compared with those of test and numerical simulation at four kinds of temperatures.The results show that with high significance and fitting degree,the regression model is reliable.

numerical simulation;regression orthogonal test;aluminum alloy;warm forming;springback; regression model

10.11817/j.issn.1672-7207.2017.10.005

TG376.2

A

1672−7207(2017)10−2590−07

2016−12−06；

修回日期：2017−03−10

国家自然科学基金资助项目(11472072, 51775160) (Projects(11472072, 51775160) supported by the National Natural Science Foundation of China)

赵坤民，博士，教授，从事汽车车身轻量化技术与先进制造技术研究；E-mail: kmzhao@dlut.edu.cn