一种采用同型号电机互为负载的直线电机推力波动测试方法

周振宇，周海波，段吉安，王伟华



一种采用同型号电机互为负载的直线电机推力波动测试方法

周振宇，周海波，段吉安，王伟华

(中南大学高性能复杂制造国家重点实验室，湖南长沙，410083)

针对传统推力波动测试方法精度不高、结构复杂的问题，提出一种采用同型号直线电机互为负载来测量直线电机推力(PMLSM)波动的方法。根据直线电机中齿槽效应和端部效应的作用机理，将2套同种型号的永磁直线电机刚性连接互为负载，通过改变电机动子之间的相位差来测量两直线电机叠加推力波动进而得到单个电机的推力波动。首先，通过分析推力波动中定位力和纹波推力与位移速度的关系，建立关于电机动子间位置差、相位差的数学模型，并进行叠加推力波动有限元分析；然后，通过改变动子间相位差进行推力波动测试，研究叠加推力随相位差改变的波动规律；最后，采用数字滤波和傅里叶变换，研究从叠加推力波动信息中精确提取单个电机推力波动的方法，得到与有限元分析结果基本一致的定位力和推力波动波形。研究结果表明：该方法能快速、精确地测量直线电机推力波动，且具有较高的测量精度。

推力波动；定位力；负载；PMLSM

永磁同步直线电机以其高速度高加速度、结构简单、定位精度高等优点，在驱动系统中有极其广泛的应用。在高精密的运动平台中，直线电机的推力波动对平台运动的效果影响尤为明显，推力波动使电机产生振动和噪音，增加了电机的控制难度，降低了电机的定位精度[1]，因此，需要通过测试推力波动来优化直线电机结构进而减小推力波动。推力波动主要由定位力和纹波推力组成。国内外对直线电机推力波动的研究主要在电机本体的优化[2−4]，控制电流来抑制或者补偿波动等[5−8]，而其中的测试方面普遍采用旋转电机带动滚珠丝杠作为负载进行测试，但是其旋转电机的转矩波动以及转接装置传动带来的干扰大大影响测试的精度，因而测量结果与真实值存在较大误差。为了使直线电机具有更好的伺服性能，必须控制好推力波动，因而，准确、迅速地检测电机的推力波动，是验证直线电机样机性能的最直接途径。然而，国内外对于直线电机优化后的推力波动测试大多只有验证性试验[9−10]，但都叙述得不详细，测量精度也不高，有的甚至没有通过实际测量，仅依靠仿真来验证设想的正确性[11−12]。苏焕宇等[13]以旋转电机作为陪测电机以滚珠丝杠作为转换传动装置，设计了一套直线电机测试平台，测试内容丰富但精度不高。MENG等[14]利用PI控制来抑制直线电机振动，在测试环节中用加速度传感器测量的加速度值通过计算得到电机波动，但无负载且需要转换计算影响测试准确度。WANG等[15]同时是通过优化控制算法来减小波动，测试通过悬挂重物，直线电机直接拉动负载，测试内容单一且未考虑摩擦。LIU等[16]将2台同样的电机平行放置，2台电机通过力传感器连接，这样虽然能够测量推力，但因电机拖动一侧负载较大、扭矩较大，容易引起测量误差。吴红伟等[17]通过2个动子叠加实验，虽与本文所述测试方法类似，但是没有测试不同相位差的波动变化，也没有分析不同条件下对波动影响的情况。本文作者采用文献[18]中的测试思路，以同型号电机互为负载来测试直线电机推力波动，通过控制两电机动子之间的距离来调整相位差，测试不同相位差下的推力进而分析电机的推力特性。通过分析直线电机推力波动成因并以此建立测试的数学模型和有限元仿真模型，比较分析仿真结果和实测计算结果，证明该测试方法的准确性。

1 直线电机推力波动成因分析

在理想条件下，永磁直线电机通入标准的正弦波形电流，电机可以产生恒定不变的推力。但是，由于电机动子磁场开断，导致齿槽效应和端部效应；永磁体励磁无法形成标准的正弦磁场，电机通入的电流不是正弦交变电流，因此，直线电机产生推力波动不可避免。

以单边永磁直线电机为测试对象，其多为平板式结构，分为动电枢式和动磁极式，动电枢式运行性能好推力密度高，动磁极式则无需拖动电缆安全性好，其主要结构如图1所示。

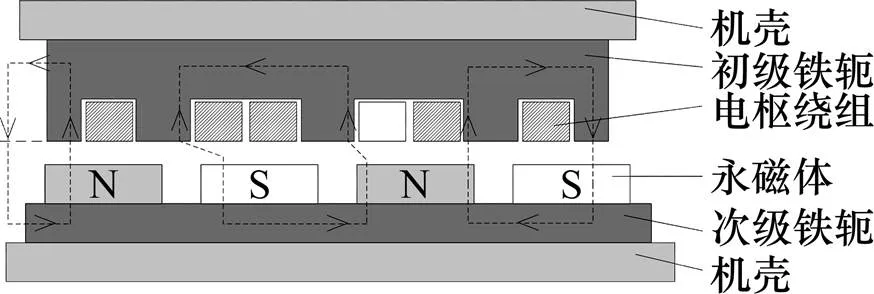
图1 永磁直线电机结构

单边永磁直线电机会产生法向吸力和水平推力，其中法向吸力是永磁体对铁芯的吸引力，最终作用在导轨上随动子运动产生摩擦力扰动。水平推力则驱动电机直线运动，主要由定位力和纹波推力组成。

1.1 定位力分析

定位力包括由端部效应生成的端部定位力和由齿槽效应生成的齿槽定位力。直线电机动子由于铁芯开放式结构有2个端部，随着铁芯与永磁体相对位置的变化，2个端部受到的磁吸力周期变化且不平衡，形成了随铁芯位置变化的端部力，两端的端部力性质相同方向相反，可表示为

将端部力表示为傅里叶级数展开式：

由式(1)和式(2)可得端部定位力的合力为

齿槽力由电机动子铁芯与定子磁场相互作用产生，因为永磁直线电机的初级是以硅钢片叠加而成，初级铁芯必须开槽以容纳线圈，这导致每个槽的开口处气隙磁场变化，在电机运动过程中产生周期性变化波动。其齿槽力是与动子位置有关的交变量，是动子位置与定子磁场的三角函数，用傅里叶级数表达为

则电机动子受到的齿槽力可以看作每一个永磁体单独作用产生的齿槽力叠加，可以得到齿槽力为

式中：b为第块永磁体单独作用时的齿槽力；为极距；为位移；为永磁体个数；为各级数相位。

由式(3)和(5)可知：端部力和齿槽力共同引起的定位力，可表示为

1.2 纹波推力分析

理想的永磁直线电机初级电流和初级反电动势都是标准正弦波形，若永磁直线电机为三相、两极，忽略齿槽效应和端部效应，次级无限长，电机三相绕组通入三相对称正弦交流电流：

式中：m为电流幅值；为电流角频率；为A相电流初始相位角。

假设气隙磁密按正弦规律变化，那么三相反电动势ma，mb和mc幅值相同，相位分别相差2π/3和4π/3 。电机推力为

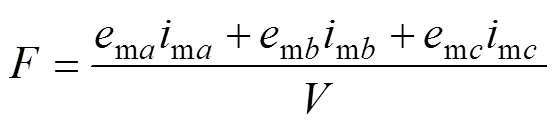
在理想条件下，电机推力正比于初级电流，基本无推力波动。但是在实际中由于电枢电流和反电动势都不是正弦波形，含有高次谐波则实际推力可写为

式中：为极距；为电流角频率；为速度；0为电机平均推力；6n为纹波推力幅值。

综合以上分析，电机运行时推力波动主要由齿槽力、端部力和纹波推力组成，其中齿槽力和端部力在电机未通电时也存在。本文拟用常见的单边永磁同步直线电机为例进行研究，根据电机的齿槽效应和端部效应作用机理，对测试方法展开分析。

2 同型号电机互为负载的推力波动测试方法

2.1 测试原理与测试方案设计

本文采用同型号电机互为负载的直线电机推力波动测试方法，在1条直线导轨上安装2台同型号直线电机并用力传感器相连，通过控制2台电机动子之间的距离来调整相位差，测试不同相位差下的推力进而分析电机的推力特性。将2台直线电机动子用丝杆分别与力传感器相连，同时，2台电机动子在1条导轨上两者所受摩擦力相同。与传统的旋转电机作为驱动悬挂重物作为负载的测试方法相比，没有引入旋转电机作为陪测电机的未知转矩波动，也排除了传动过程中的摩擦干扰和其他不确定性。

推力波动测试的原理如图2所示，2个型号相同的动子通过力传感器用丝杆相连，2动子之间的距离即相位差可调。对陪测直线电机电枢通电，被测电机不通电，拉动2台电机动子匀速运动，此时，力传感器采集的推力与位置的变化即为该相位差下2台电机推力的耦合，此时的推力波动为2台电机的定位力波动与陪测电机纹波推力的叠加。调节2台电机动子间距离，重复1遍以上过程，则得到另一个相位差下推力的耦合数据。

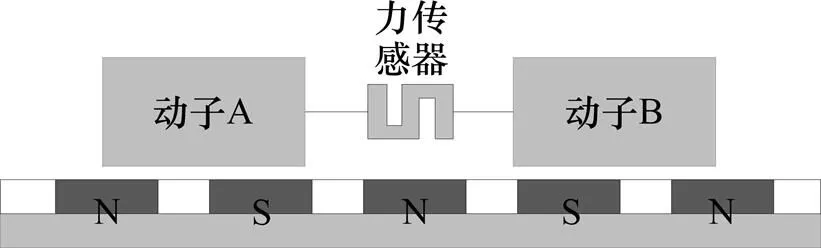
图2 测试原理结构图

从图2可知：力传感器测得的力为两动子之间的合力，若要准确得到电机的定位力与纹波推力必须将合力进行解耦。假设两动子间距离为1个极距，此时的相位差为。以动子A的位置为初始位置，由式(6)可知动子A的定位力。若A和B两动子间相位差为，则动子B上的定位力可以表述为

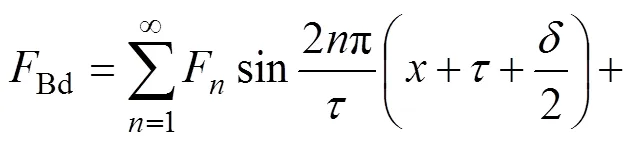
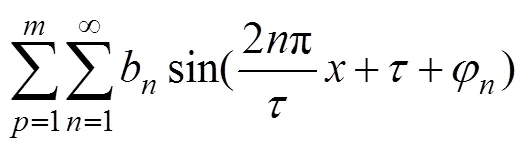
测量过程中由动子A拉动子B做匀速运动，此时作用在动子B上的力除了定位力Bd外，还有摩擦力f和动子B匀速运动的磁阻力BZ；动子A通电拖动力传感器和动子B匀速运动，其受到自身的定位力Ad与摩擦力f外，还有电枢通电后促使动子的向前匀速运动的推力。力传感器测量到的力F可以表示为

在式(11)中，动子A的摩擦力f与动子B的摩擦力f由于处于同样的环境下，因此，可以认为两者相等，磁阻力BZ在匀速运动时为恒定常量。若以动子A的位置为参考点，动子B与A的距离为，则式(11)可以表述为

在同样条件下，只改变A与B的距离，动子A的起始位置不变，仍然保持相同的速度匀速运动，可以得F2，2台电机动子虽然改变距离，但其他外部条件均相同，把2种不同距离下力传感器测到的数据对应相减，可得

通过以上分析可知，只需要改变动子间距离，就可以将力传感器测量到的数据进行解耦得到2台电机定位力耦合波形。若距离L取/2的奇数倍，由式(6)和(13)可得电机在不同位置下的定位力波形。

2.2 推力测试仿真分析

以测试用的永磁直线电机为模型，利用ANSOFT软件对其进行有限元仿真，具体参数如表1所示。

表1 直线电机主要技术参数

根据表1中参数建立永磁直线电机模型，进行瞬态仿真得到电机磁感应强度分布图，如图3所示。从图3可知：气隙处的磁感应强度并不是有规律地分布，并且在端部也有很多磁力线，这也就导致了齿槽效应和端部效应。

在电机不通电的情况下，设置电机在0.1 m/s下空载匀速运动，仿真得到如图4所示。由前面分析可知定位力在未通电下仍然存在，从图4可以看出定位力随时间呈周期性变化，是位移的周期性函数且力的平均值约为0 N。

参照前面分析的数学模型，力传感器测量的推力为互为负载的2条直线电机相互作用的合力。若设置电机A通电并拖动电机B做匀速运动，且2台电机动子间相对距离为奇数倍/2和偶数倍/2，根据式(10)分别进行仿真计算，得到如图5和图6所示推力波形。从图5和图6可知：由于仿真设置的输入电流为标准正弦交变电流，所以，图中没有电流的高次谐波引起的纹波推力，同时可以看到2台电机动子在奇数倍/2距离下波动明显比在偶数倍/2距离下的波动大。

图3 磁感应强度分布图

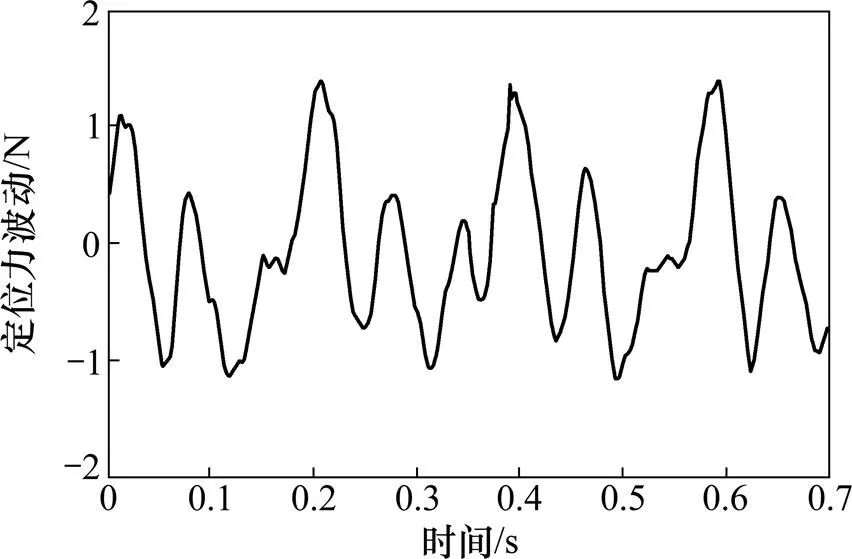
图4 定位力仿真波形图

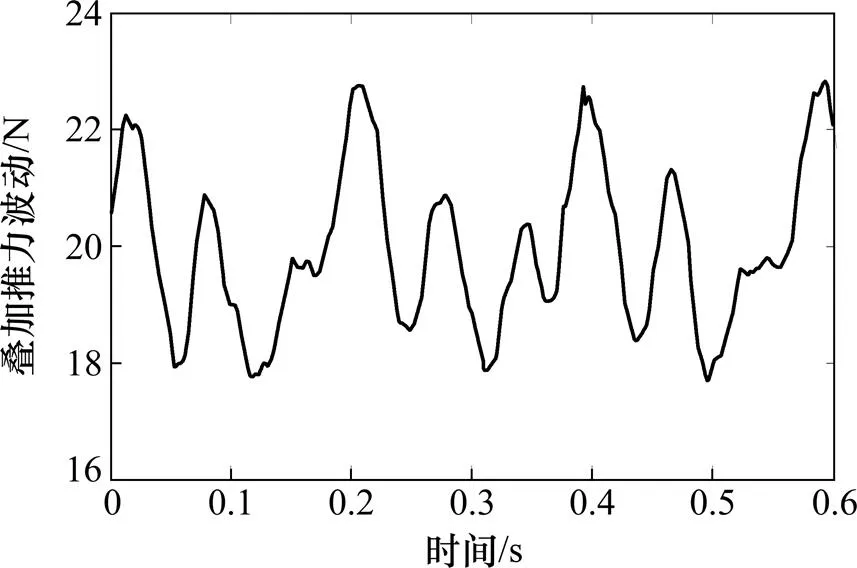
图5 τ/2奇数倍的直线电机推力波动仿真波形图

图6 τ/2偶数倍的直线电机推力波动仿真波形图

3 同型号电机互为负载的推力波动测试实验

3.1 实验装置与推力波动测试

为了测量永磁同步直线电机的推力波动，验证上节的仿真结果和理论分析，设计了一套测试系统，如图7所示。该系统由陪测直线电机和被测直线电机、力传感器、电机驱动器、电机运动控制器以及数据采集处理模块组成。测试中采用2台同型号安川直线电机其结构参数如表1所示，力传感器用电磁屏蔽铜网缠绕，用来屏蔽电机运动中因力传感器离磁场太近引起的电磁干扰。

将测试系统调试好，接通直线电机A的电源，通过EMAC运动控制器，使动子A拖动动子B以0.1 m/s速度匀速运动，由式(13)可知力传感器实时采集运动过程中的推力数据为动子A与B相互耦合的作用力。以2个动子左侧端部为参考，调节两端部之间的距离，采集和整理数据，得到力传感器采集到推力波形曲线，如图8所示，经过数字滤波滤除高阶杂波和傅里叶变换后的频谱图如图9所示。

图7 测试系统实物图

(a) 距离为261 mm波形；(b) 距离为264 mm波形；(c) 距离为267 mm波形；(d) 距离为270 mm波形；(e) 距离为273 mm波形；(f) 距离为279 mm波形

(a) 距离为261 mm频谱；(b) 距离为264 mm频谱；(c) 距离为267 mm频谱；(d) 距离为270 mm频谱；(e) 距离为273 mm频谱；(f) 距离为279 mm频谱

从图8可以看到：在261~279 mm每隔3 mm的 7组波形图和频谱图中，通过将力传感器用电磁网包裹，有效地屏蔽了电磁场带来的干扰；比较距离为 261 mm和279 mm的2个波形图发现2幅图中波形以及对应推力近乎一致，此时2个动子相对距离正好为1个极距18 mm，因此，可以认为2台电机互为负载推力耦合叠加的波形的变化周期为。从图8还可以看到：推力波形随不同相位差围绕20 N波动；推力由5 N逐渐变到2 N时接近正弦曲线，之后再变大；并且波动最小的是距离为270 mm时的波形图，而波动最大的是距离为261 mm与279 mm的波形图，波动最小的距离正好是/2的偶数倍，波动最大的是/2的奇数倍，与仿真波形得到的结果一致。图9所示为将图8中的推力数据通过高阶数据滤波和傅里叶变换后对应的频谱图。从图9可以看到：在低阶100 Hz内，幅值虽然不同，但其分布大致相同。

3.2 推力波动实验分析

根据式(13)计算可知：若取相位差为/2的偶数倍与相位差为/2的奇数倍的2个波形对应相减，由于两者距离差为半个相位差，根据三角函数的性质以及式(13)，该波形为半个相位差下定位力的叠加波形。以270 mm与279 mm的定位力波形计算，所得结果如图10所示，为基于2个不同距离下解耦得到的动子B定位力波形图与仿真波形。

由图10可知：动子B的定位力波动约为1.6 N，与直线电机B的额定推力80 N相比，在额定工作条件下定位力的波动率为2%，且实测计算波形与仿真波形基本一致。

将图10得到的定位力波形与实测波形进行比较，并结合式(13)，可以得到动子A在此时的推力波动波形图，如图11所示。

从图11可知：推力波动波形图与仿真结果的波形图变化趋势基本一致。但图10和图11所示波形都存在偏差，其主要原因是仿真模型为一种理想化模型，没有考虑实际电机结构的差别；同时，实测推力波动中包括电流的高次谐波引起的纹波推力和线缆的阻 尼力。

1—实测计算；2—仿真结果。

1—实测计算；2—仿真结果。

4 结论

1) 根据齿槽效应和端部效应的作用机理，提出了一种将2套同种型号的永磁直线电机刚性连接互为负载测量直线电机推力波动的方法。

2) 分析推力波动与位移的关系，建立了直线电机推力波动测试方法的数学模型，并在距离取/2的奇数倍时求出电机的定位力，由此得到电机的推力 波动。

3) 推力波动的仿真结果与实验结果有较好的一致性，证明了数学模型的正确性。该测试方法测试精度较高，结构简单，对直线电机推力波动测试研究具有一定的启发意义。

[1] 宋书中, 胡业发, 周祖德. 直线电机的发展及应用概况[J]. 控制工程, 2006, 13(3): 199−201. SONG Shuzhong, HU Yefa, ZHOU Zude. Review of application and development of linear motors[J]. Control Engineering of China, 2006, 13(3): 199−201.

[2] 张明超, 尹文生, 朱煜. 永磁同步直线电机推力波动建模与抑制[J]. 清华大学学报(自然科学版), 2010, 50(8): 1253−1257. ZHANG Mingchao, YIN Wensheng, ZHU Yu. Force ripple modeling and suppression in permanent magnet linear synchronous motors[J]. Journal of Tsinghua University (Science & Technology), 2010, 50(8): 1253−1257.

[3] 王昊, 张之敬, 刘成颖. 永磁直线同步电机定位力分析与实验研究[J]. 中国电机工程学报, 2010, 30(15): 58−63. WANG Hao, ZHANG Zhijing, LIU Chengying. Detent force analysis and experiment for permanent magnet linear synchronous motor[J]. Proceedings of the CSEE, 2010, 30(15): 58−63.

[4] 李庆雷, 王先逵, 吴丹, 等. 永磁同步直线电机推力波动分析及改善措施[J]. 清华大学学报(自然科学版), 2000, 40(5): 33−36. LI Qinglei, WANG Xiankui, WU Dan, et al. Thrust fluctuation analysis and reduction of PMLSM[J]. Journal of Tsinghua University (Science & Technology), 2000, 40(5): 33−36.

[5] JUNG I S, YOON S B, SHIM J H, et al. Analysis of forces in a short primary type and a short secondary type permanent magnet linear synchronous motor[J]. IEEE Transactions on Energy Conversion, 1999, 14(4): 1265−1270.

[6] 卢少武, 唐小琦, 周凤星, 等. 永磁同步直线伺服系统的纹波推力补偿[J]. 西安交通大学学报, 2014, 48(2): 106−110. LU Shaowu, TANG Xiaoqi, ZHOU Fengxing, et al. Force ripple compensation for permanent magnet linear servo system[J]. Journal of Xi’an Jiaotong University, 2014, 48(2): 106−110.

[7] 徐月同, 傅建中, 陈子辰. 永磁直线同步电机推力波动优化及实验研究[J]. 中国电机工程学报, 2005, 25(12): 122−126. XU Yuetong, FU Jianzhong, CHEN Zichen. Thrust ripple optimization and experiment for PMLSM[J]. Proceedings of the CSEE, 2005, 25(12): 122−126.

[8] 夏加宽, 董婷, 王贵子. 抑制永磁直线电机推力波动的电流补偿控制策略[J]. 沈阳工业大学学报, 2006, 28(4): 379−383. XIA Jiakuan, DONG Ting, WANG Guizi. Current compensation control strategy for restraining thrust fluctuation of PMLSM[J]. Journal of Shengyang University of Technology, 2006, 28(4): 379−383.

[9] 刘泉. 永磁同步直线电机推力特性的静态与动态测试[J]. 北京信息科技大学学报(自然科学版), 2014, 29(4): 21−24. LIU Quan. Static and dynamic measurement for thrust performance of permanent magnet synchronous linear motor[J]. Journal of Beijing Information Science and Technology University, 2014, 29(4): 21−24.

[10] ZHANG L, KOU B, ZHANG Y, et al. Thrust characteristic analysis and test of the synchronous permanent magnet linear motor[C]//Electrical Machines and Systems (ICEMS), 2014 17th International Conference on. Hangzhou, China, 2014: 1733−1737.

[11] ZHAO J, LIU K, CHEN P, et al. Reduction of detent force in permanent magnet linear synchronous motor with double secondary side[C]//Electrical Machines and Systems (ICEMS), 2014 17th International Conference on. Hangzhou, China, 2014: 1274−1278.

[12] REMY G, KREBS G, TOUNZI A, et al. Detent force calculations of a PMLSM using the finite element method[J]. IEEJ Trans Ind Appl, 2009, 129(5): 462−469.

[13] 苏焕宇, 尹韶辉, 谌国权, 等. 一种永磁直线同步电动机的实验和测试装置[J]. 制造技术与机床, 2012(10): 112−114. SU Huanyu, YIN Shaohui, CHEN Guoquan, et al. Experiment and examination equipment for permanent magnet synchronous linear motor[J]. Manufacturing Technology and Machine Tool, 2012(10): 112−114.

[14] MENG F, LIU C, LI Z, et al. Adaptive PI control strategy for flat permanent magnet linear synchronous motor vibration suppression[J]. Chinese Journal of Mechanical Engineering, 2013, 26(1): 11−20.

[15] WANG H, FENG H, SI J, et al. Simulation and test study on direct force control for permanent magnet linear synchronous motor[J]. Journal of Computers, 2013, 8(3): 733−740.

[16] LIU Ruozhu, YANG Qingdong, TONG Liang. Thrust ripples test and analysis of permanent magnet linear synchronous motor[C]//Measuring Technology and Mechatronics Automation (ICMTMA), 2011 Third International Conference on. Shanghai, China, 2011: 1017−1022.

[17] 吴红伟, 杨家军, 程远雄. 新型永磁同步直线电机的有限元分析和实验研究[J]. 机电工程, 2013, 30(5): 541−544. WU Hongwe, YANG Jiajun, CHEN Yuanxiong. Analysis and experimental research of a new type of permanent magnet linear synchronous motor[J]. Journal of Mechanical & Engineering, 2013, 30 (5): 541−544.

[18] 王伟华, 张子娇, 周海波, 等. 一种同步直线电机推力波动特性的检测方法[J]. 中国电机工程学报, 2016, 36(2): 540−546. WANG Weihua, ZHANG Zijiao, ZHOU Haibo, et al. A method for detecting the thrust fluctuation characteristics of synchronous linear[J]. Proceedings of the CSEE, 2016, 36(2): 540−546.

(编辑 杨幼平)

Thrust fluctuation measurement of PMSLM by the same model motor of mutual load

ZHOU Zhenyu, ZHOU Haibo, DUAN Ji’an, WANG Weihua

(State Key Laboratory of High Performance Complex Manufacturing,Central South University, Changsha 410083, China)

Aimed at the low measuring precision and complex construction in traditional thrust fluctuation test, a novel method for the thrust fluctuation measurement of PMSLM by the same model motor of mutual load was proposed. According to the principle of cogging effect and end effect, the two same types of permanent magnet linear motors were rigidly connected and mutually loaded by moving the distance between the two motors. Then phase difference was adjusted to measure the thrust fluctuation of the motors. The relationship of detent force and thrust ripple between displacement and velocity was analyzed. The mathematic model and the finite element model were established. Then the experiments of thrust ripple were carried out, to study the superposition thrust regular fluctuation with phase difference. And the force of different distances was contrasted by digital filtering and Fourier transform, which studied the method of extracted thrust wave from two-motor thrust coupling fluctuation under different phases. The results show that this method can measure the thrust fluctuation quickly and accurately.

thrust ripple; detent force; load; PMLSM

10.11817/j.issn.1672−7207.2017.10.012

TM93

A

1672−7207(2017)10−2641−08

2016−10−15；

修回日期：2016−12−02

国家自然科学基金资助项目(51575534)；国家科技重大专项(2012ZX02702006)；湖南省自然科学基金资助项目(2015JJ4078)；高性能复杂制造国家重点实验室自主课题(ZZYJKT2015-10)(Project (51575534 ) supported by the National Natural Science Foundation of China ; Project (2012ZX02702006) supported by the Natural Science and Technology Major Program of China; Project (2015JJ4078) supported by the Natural Science Foundation of Hunan Province; Project (ZZYJKT2015-10) supported by Self-selected Topic Fund of State Key Laboratory of High Performance Complex Manufacturing)

周海波，博士，副教授，从事机电系统设计、建模与控制研究；E-mail：zhouhaibo@csu.edu.cn