大型数控成形磨齿机热误差建模及补偿

周宝仓，王时龙，方成刚，杨勇



大型数控成形磨齿机热误差建模及补偿

周宝仓1，王时龙1，方成刚2，杨勇3

(1. 重庆大学机械传动国家重点实验室，重庆，400044；2. 南京工业大学机械与动力工程学院，江苏南京，210009；3. 重庆机床(集团)有限责任公司，重庆 401336)

基于大型数控成形磨齿机热误差是影响齿面加工精度的重要因素，通过建立磨齿机热误差实验平台，研究砂轮与工件轴的径向热误差随温度变化的关系。结合模糊聚类法基本原理和最小二乘法理论，建立砂轮与工件轴的径向热误差补偿模型，并将补偿模型的计算值与实验检测值进行对比。进行热误差补偿加工实验，验证热误差补偿模型的准确性与可靠性，揭示成形磨齿机热误差与温度之间的关系。研究结果表明：该误差模型的补偿精度高、可靠性好，与实验测量值的相对误差小于2.000%，可有效提升齿面整体加工精度(ISO) 3级以上。

数控成形磨齿机；热误差；模糊聚类；最小二乘法；误差补偿模型

大型数控成形磨齿机是一种高效、精密的齿轮加工设备，广泛应用于风电、水电、船舶、工程机械等重型装备领域的大规格、高精度齿轮加工。在加工齿轮工件时，磨齿机需长时间连续运行，其导轨、滑块、丝杠等运动部件因相互摩擦等逐渐产生大量的热，再加上电机发热、砂轮与工件的磨削热等多种热源的影响，机床温度会逐渐升高并产生相应的热变形，造成砂轮与工件之间产生相对位置误差，从而严重影响齿轮的加工精度[1]。尤其是随着磨削速度、电机功率、加工效率的不断提升，机床热变形导致的齿面加工误差(简称热误差)可占机床加工总误差的70%[2]。建立高精度、高可靠性的机床热误差补偿模型，是提高机床加工精度的重要保证。为此，国内外研究者进行了广泛的研究和探索，通过神经网络理论、贝叶斯网络理论、模糊控制理论、灰色系统理论等多种人工智能理论以及遗传算法、有限元法、多元线性回归等多种误差补偿方法建立机床的误差模型[3−9]。刘明等[10]运用多体系统理论与神经网络方法建立了机床通用误差计算模型、温度与变形参数模型，并在Makino四轴加工中心进行了实验验证，达到了误差补偿预期效果。KIM等[11]运用有限元方法建立了机床滚珠丝杠系统的温度场模型。张毅等[12]结合灰色模型和神经网络理论的优点，建立了机床热误差预测模型并验证了模型的补偿精度。陶晓杰等[13]从机床主要部件的结构出发，对机床热变形进行了简略推导，得到了机床热误差对刀具与工件间的相对位置的影响规律。陈彧龙[14]分析了滚齿机加工热变形现象及热变形对齿轮加工精度的影响，并提出了一种滚齿机热误差的新型检测方案。虽然这些研究对机床热误差产生机理及误差控制方法进行了探索，但大型数控磨齿机尺寸庞大、结构复杂、热源广泛，其热误差产生原因纷繁复杂，并且机床各部位的温度变量间相互作用和影响，使得单从理论角度对磨齿机进行热误差分析并建立高精度、高可靠性的误差补偿模型显得十分困难。在保证砂轮修形精度的前提下，机床热误差导致的砂轮与齿轮工件轴的径向位置误差对齿面加工精度起到了决定性作用，故研究砂轮、齿轮工件轴的热误差变化规律，是建立磨齿机误差补偿模型的前提。为探明磨齿机热误差变化规律并建立精确的热误差补偿模型，本文作者以某大型数控成形磨齿机为研究对象，通过建立热误差实验平台，获得机床温升与砂轮、工件轴的径向热误差变化情况。在此基础上，运用模糊聚类回归法的基本原理，对多个温度变量进行相关性分析，从中选出9个关键的温度变量。最终，采用多元线性回归-最小二乘法理论建立机床热误差补偿模型；通过热误差补偿加工实验，验证了模型的准确性与可靠性。

1 大型数控成形磨齿机温度测量点的选择与优化

1.1 磨齿机的基本结构

图1所示为某大型数控成形磨齿机基本结构图。该型磨齿机的和轴采用静压导轨；床身、数控转台均为独立结构且采用多个螺栓连为一体；床身及数控转台底座均通过垫铁、地脚螺栓与地基固定，使得整个机床具有良好的抗冲击、振动、位移能力。另外，该型磨齿机外形尺寸庞大、结构复杂、运动部件众多，在摩擦热、磨削热等多种内外热源的共同作用下，机床导轨、丝杠、电主轴、数控转台等多个部位会发生不同程度的温升而出现温度梯度，造成机床出现相应的热变形(见图2)，使得砂轮与齿轮工件轴产生位置误差，最终严重影响齿面加工精度。

1.2 磨齿机温度测量点的选择与优化

为探明磨齿机在长时间生产加工过程中的温度场，以某型大型数控成形磨齿机为研究对象，依据其结构特点及运动部件的温升情况，在机床主要受热部位设置26个温度传感器T(=1，2，…，26)。由于在成形磨齿过程中，砂轮与工件沿机床坐标系方向的相对位置误差Δ仅会影响齿面在齿轮圆周上的位置，而对齿面本身不会产生任何影响[8]。另外，砂轮、工件轴沿机床坐标系方向的位置误差对齿轮加工精度的影响尤为明显。因此，分别在检测砂轮、工件轴的径向位置安装相应的激光位移传感器A和B，测得的位移分别为Δw和Δg。

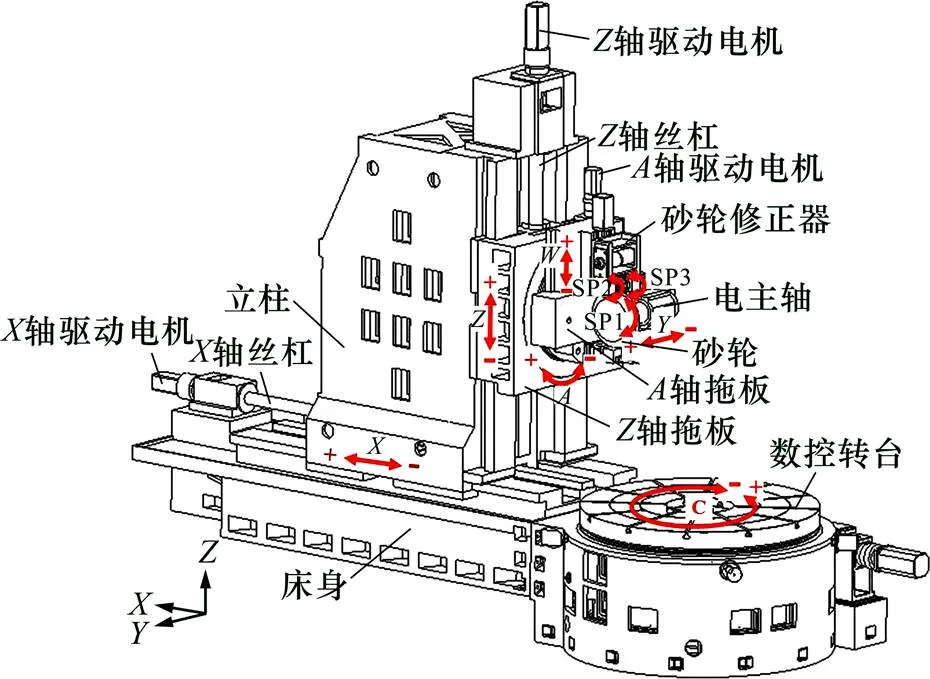
图1 某大型数控成形磨齿机基本结构图

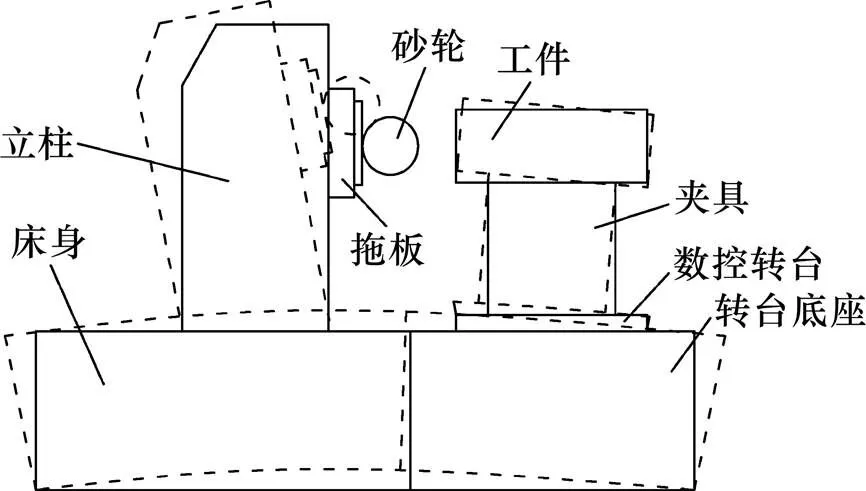
图2 大型数控成形磨齿机热变形示意图

图3所示为温度、位移测量点位置布置图。采用带热电阻(Pt100)传感器的MIK5010A数据记录仪、LTS-25-02型激光位移传感器分别记录测量点的温升、位移情况。实验期间，车间的环境温度为 (20±0.2) ℃，热电阻传感器的检测精度为0.01 ℃，激光位移传感器的检测精度为0.01 μm，砂轮工作转速为1 800 r/min。每分钟采集1次温度−位移数据，砂轮、工件轴随时间的径向热误差变化曲线如图4所示。

由图4可以看出：随着磨齿机长时间连续运行，在前3 h内，砂轮、工件轴的径向热误差曲线随着时间的增加而迅速增大；在3~4 h内，两者的误差曲线增长速度逐渐减缓，机床趋于热平衡状态；在4 h以后，曲线的变化近似于直线，表明机床完全达到热平衡状态。另外，图中砂轮、工件轴径向热误差曲线的连续性较好，无突变、断崖等现象，表明磨齿机本身具有优异的设计及结构特性，有利于实现更好的误差补偿效果。

磨齿机结构复杂、热源众多，各个热源间会产生相互作用，导致机床热误差补偿模型中的各个温度变量间出现变量耦合关系，从而降低补偿模型的准确性和鲁棒性[9]。对此，依据模糊聚类法基本原理[10]，先将机床温度与对应的位移变量进行相关性分析，把多个温度−位移变量间相关系数相近的归为1类；然后从中选取相关系数最大的温度变量为该类代表；最终，将各温度变量代表作为1个温度变量组用于磨齿机热误差建模。

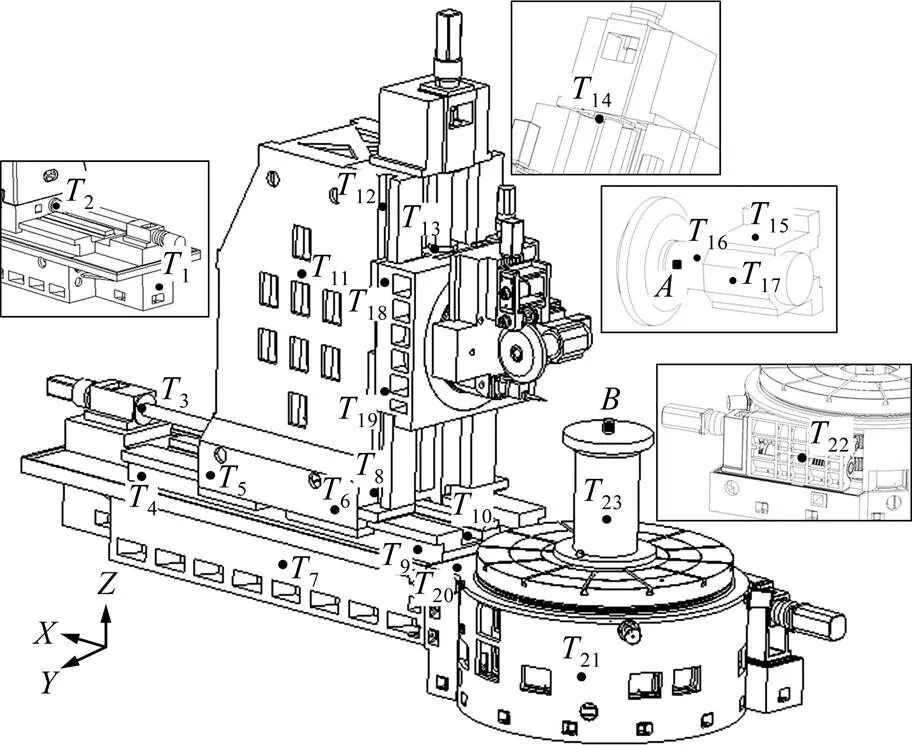
图3 温度、位移测量点位置示意图

1—Δxw；2—Δxg

磨齿机第个温度测量点的温度变量与位移变量Δx的相关系数r为

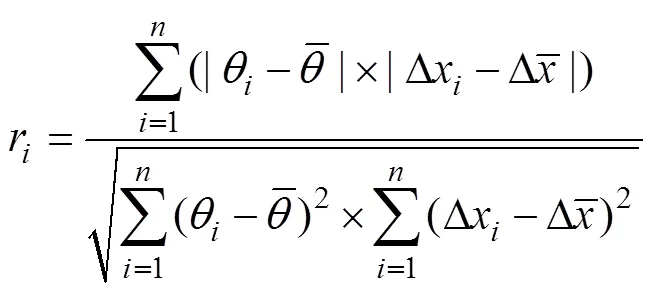
由式(1)可计算得到砂轮的径向热误差与温度变量的相关系数，如表1所示。

将表1中相关系数相近的温度变量归为1组，则有温度变量组{21，26}，{1，7，11}，{6，8，20}，{10，13，18}，{5，19，23，24}，{4，9，12，17}，{2，3，14，15，22}，{16，25}。与其他温度变量组相比，{21，26}和{1，7，11}的相关系数较小，因而对砂轮径向热误差的影响亦较小。为了降低热误差模型的维数，可将温度变量组{21，25}与{1，7，11}舍去，然后分别从其他各变量组中选取相关系数最大的变量。则用于砂轮径向热误差Δw建模的温度变量为2(轴丝杠螺母座)、8(轴导轨下端)、9(轴导轨前端)、13(轴丝杠螺母座)、16(电主轴前端)、24(冷却站进油口油温)。

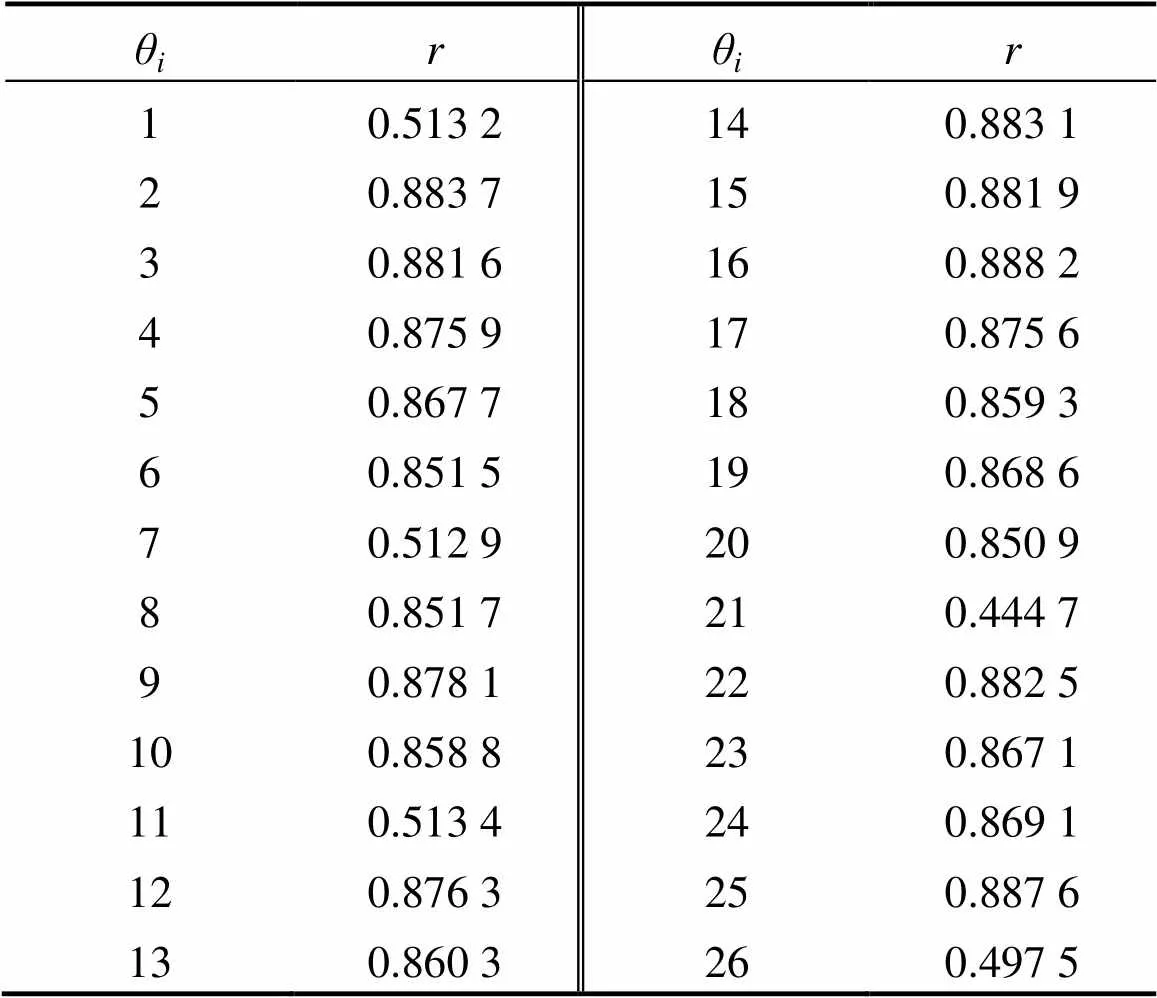
表1 砂轮的径向热误差与温度变量的相关系数r

同理，用于工件轴径向热误差Δg建模的温度变量为9(轴导轨前端)、20(转台台面)、22(转台蜗轮蜗杆啮合部位)、23(工件夹具)、24(冷却站进油口油温)。

2 磨齿机热误差补偿模型的建立

运用聚类分析法对温度变量进行优选后，可采用多元线性回归分析中的最小二乘法，建立整体性好、鲁棒性强、精度高的机床热误差补偿模型。该方法结构简单、性能可靠、逼近精度较高，是机床热误差建模领域最有效的建模方法之一[11]。

由于Δw与经过优选的温度自变量导线性关系，依据多元线性回归理论，Δw与的数学模型为

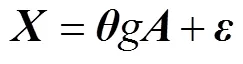
设a(=0，1，2，…，6)为0~6的最小二乘估计参数，则方程组(2)可转化为

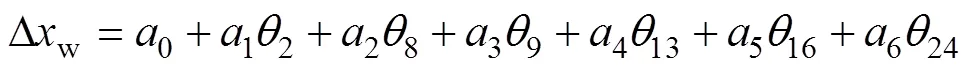
依据最小二乘法原理，对于估计参数a，需使Δw的残差平方和达到最小值，即

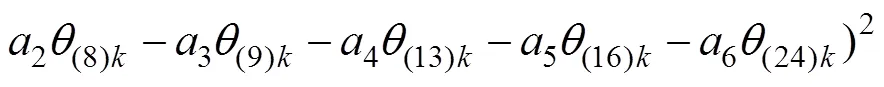
在最小值处的偏导数为0，即

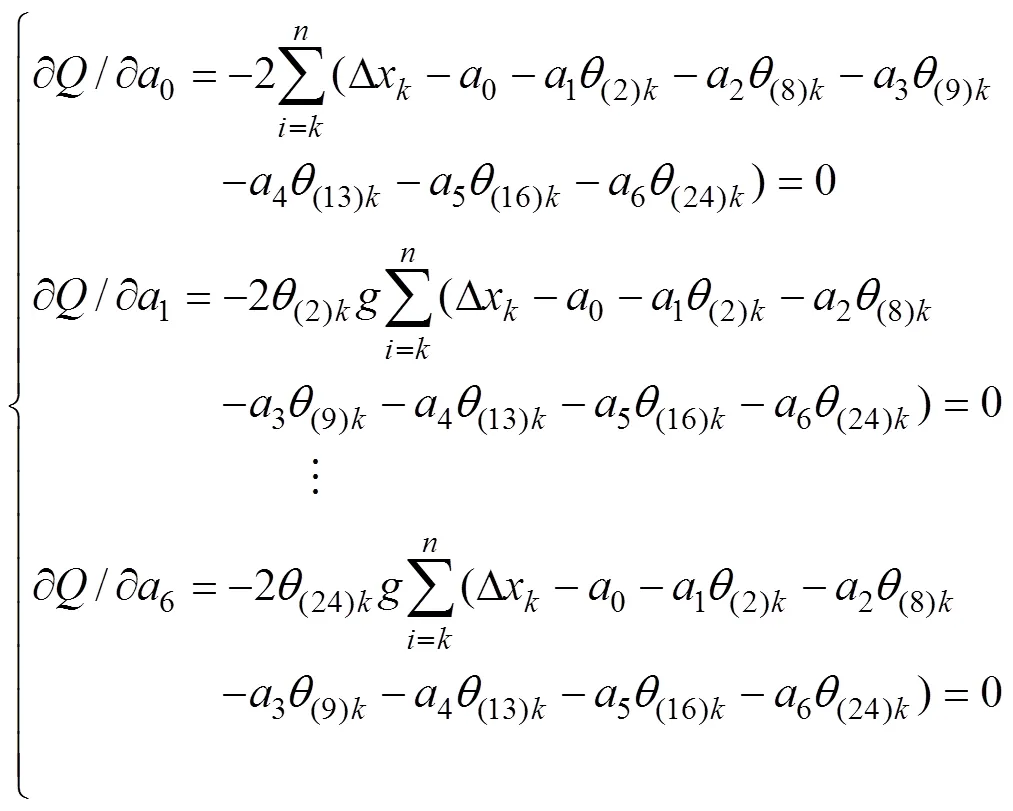
将实验测量值Δwk，(2)k，(8)k，(9)k，(13)k，(16)k和(24)k代入式(5)，解得回归参数a并代入式(3)，即可得到砂轮径向的误差Δw与的误差补偿模型方程：

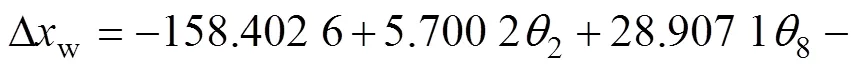
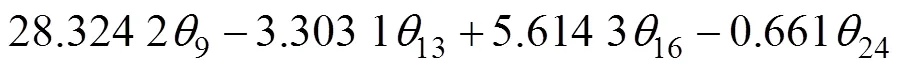
同理，工件轴热误差Δg与优选后的温变量度的误差补偿模型方程为

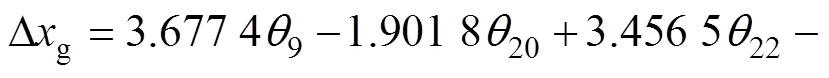
3 热误差模型分析

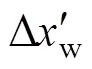
1—；2—；3—；4—。

将砂轮与工件轴径向热误差的实验测量曲线与补偿模型曲线进行对比可知：在磨齿机未达到热平衡状态时，实验测量值与模型计算值相比，出现时大时小的情形。这是因为磨齿机零部件间有着一定的装配间隙；各部件的金属种类不同，热膨胀系数也不同，使得各个零部件存在温升以及热膨胀不均匀现象；机床内部液压油因温度较低出现轻微的粘滞现象，使得导轨接触面未得到充分润滑，受摩擦力相对较大等因素的影响，砂轮与工件轴的径向热误差出现非均匀、非线性增长；当磨齿机达到热平衡状态后，机床各部位间的温升、运动导轨副间的阻力、零部件的热膨胀等达到了稳定状态，热误差曲线不再随加工时间的变化而出现较大的变化，近似呈直线状态，与磨齿机的实际工作情形相符。但由于受到砂轮修形精度、砂轮转动的不平衡性、磨削振动、冷却液流量和喷淋位置、机床部件装配误差以及数控转台涡轮蜗杆的摩擦振动等众多因素的影响，热平衡后的实验测量值均大于补偿模型计算值。

4 磨齿机热误差的补偿过程及其加工实验

对磨齿机进行热误差建模及补偿的最终目的是提高成形磨齿加工后的齿轮精度。因此，以砂轮、工件轴热误差补偿模型为基础，运用软件在线补偿的方式，在南京工大数控有限公司的某大型数控成形磨齿机上，进行热误差补偿加工实验。在筛选优化后的机床重要部位布置相应的热电阻(Pt100)温度传感器，通过PLC模块采集温度信号并转换为PLC存储字节，数控系统参数读取字节，获得反馈的温度；嵌入机床数控系统的热误差补偿模块直接读取由参数得到的温度并计算出砂轮、工件轴的实际径向热误差；磨齿机数控系统读取该误差后，通过调整轴驱动电机的脉冲数，对砂轮径向位置误差进行补偿；通过调整数控转台力矩电机的脉冲数，对工件轴的径向位置误差进行补偿，从而实现磨齿机热误差的实时在线补偿。相关补偿参数的调整均可在数控系统中完成，无需增添机械调整装置。磨齿机热误差补偿相关流程如图6 所示。

图6 大型数控成形磨齿机热误差补偿流程图

补偿实验所加工的齿轮工件的法向模数为 14 mm，齿数为35，压力角为20°，螺旋角为30°。利用江苏省工业装备数字制造及控制技术重点实验室的WENZEL (LH1512)三坐标测量机，检测误差补偿前后的齿轮齿廓形状偏差、齿廓倾斜偏差和齿廓总偏差。实验期间，车间温度为(20.1±0.2) ℃，三坐标检测室室温为(20.2±0.1) ℃，三坐标测头的直径为4.99 mm。

误差补偿前，齿轮左、右齿面的最大齿廓倾斜偏差分别为37.7 μm和30.8 μm；误差补偿后，左、右齿面的最大齿廓倾斜偏差分别减小至4.9 μm和4.3 μm。与补偿前相比，齿廓倾斜偏差分别减少33.8 μm和26.5 μm，精度等级(ISO)由8级提高至2级；齿廓总偏差(ISO)由8级提高至5级，补偿效果明显。机床热误差补偿模型结果与实验结果一致性好，模型精度高，实用性强，能够满足实际生产的需要，可以有效提高齿轮加工精度。

5 结论

1) 采用模糊聚类回归法对机床的多个温度变量进行优选；依据多元线性回归-最小二乘法的基本原理建立砂轮、工件轴的径向热误差补偿模型。

2) 经过分析，砂轮、工件轴的径向热误差模型的补偿精度与实验测量值的相对误差均低于2.000%，表明补偿模型曲线的拟合程度较好、补偿精度高。

3) 该热误差补偿模型可有效减小齿面误差，提升齿面整体加工精度(ISO) 3级以上，从而验证了模型的准确性与可靠性。

[1] KANG Y, CHANG C W, HUANG Y, et al. Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools[J]. International Journal of Machine Tools and Manufacture, 2007, 47(2): 376−387.

[2] WU H, ZHANG H T, GUO Q J, et al. Thermal error optimization modeling and real-time compensation on a CNC turning center[J]. Journal of Materials Processing Technology, 2008, 207(1/2/3): 172−179.

[3] 余文利, 姚鑫骅, 傅建中, 等. 贝叶斯证据框架下的LS-SVM多工况数控机床热误差建模[J]. 中国机械工程, 2014, 25(17): 2361−2368. YU Wenli, YAO Xinhua, FU Jianzhong, et al. Modeling ofCNC machine tool thermal errors based on LS-SVM within Bayesian evidence framework[J]. Journal of China Mechanical Engineering, 2014, 25(17): 2361−2368.

[4] CAO Huajun, ZHU Libin, LI Xianguang, et al. Thermal error compensation of dry hobbing machine tool considering workpiece thermal deformation[J]. International Journal of Advanced Manufacturing Technology, 2016, 86(5/6/7/8): 1−13.

[5] 李永祥, 杨建国, 李昱瑶, 等. 基于灰色系统的机床热误差建模研究[J]. 武汉理工大学学报, 2007, 29(1): 58−61. LI Yongxiang , YANG Jianguo , LI Yuyao, et al. Application of grey system model to thermal error modeling on machine tools[J]. Journal of Wuhan University of Technology, 2007, 29(1): 58−61.

[6] 余治民, 刘子建, 艾彦迪, 等. 基于神经模糊控制理论的数控机床热误差建模[J]. 中国机械工程, 2014, 25(16): 2225−2231. YU Zhimin, LIU Zijian, AI Yandi, et al. Thermal error modeling of NC machine tool using neural fuzzy control theory[J]. Journal of China Mechanical Engineering, 2014, 25(16): 2225−2231.

[7] Abdulshahed A M, Longstaff A P, Fletcher S, et al. The application of ANFIS prediction models for thermal error compensation on CNC machine tools[J]. International Journal of Applied Soft Computing, 2015, 27(7): 158−168.

[8] Wang Liping,Wang Haitong,LI Tiemin, et al. A hybrid thermal error modeling method of heavy machine tools in z-axis[J]. International Journal of Advanced Manufacturing Technology, 2015, 80(1/2/3/4): 389−400.

[9] Zhang Jianfu, Feng Pingfa, Chen Chuang, et al. A method for thermal performance modeling and simulation of machine tools[J]. International Journal of Advanced Manufacturing Technology, 2013, 68(5/6/7/8): 1517−1527.

[10] 刘明, 章青. 运用多体理论和神经网络的机床热误差补偿[J]. 振动、测试与诊断, 2010, 30(6): 658−661. LIU Ming, ZHANG Qing. Thermal error model and compensation of machining tool using multibody system theory and neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(6): 658−661.

[11] KIM S K, CHO D W. Real-time estimation of temperature distribution in a ball-screw system[J]. International Journal of Machine Tools and Manufacture, 1997, 37(4): 451−464.

[12] 张毅, 杨建国. 基于灰色神经网络的机床热误差建模[J]. 上海交通大学学报, 2011, 45(11): 1581−1586. ZHANG Yi, YANG Jianguo. Grey neural network modeling for machine tool thermal error[J]. Journal of Shanghai Jiaotong University, 2011, 45(11): 1581−1586.

[13] 陶晓杰, 王治森. 滚齿机床热变形对加工精度的影响[J]. 机械传动, 2005, 29(3): 54−57. TAO Xiaojie, WANG Zhisen. Influence of thermal deformations of the hobbing machine on machining accuracy[J]. Journal of Mechanical Transmission, 2005, 29(3): 54−57.

[14] 陈彧龙, 陶晓杰. 滚齿机热变形分析与误差检测新方法[J]. 装备制造技术, 2013(5): 205−207. CHEN Yulong, TAO Xiaojie. Thermal deformation analysis and a novel error measurement proposal for gear hobbing machine tools[J]. Journal of Equipment Manufacturing Technology, 2013(5): 205−207.

[15] 张虎. 数控成形磨削齿面误差理论与修正方法研究[D]. 南京: 南京工业大学机械与动力工程学院, 2014: 81−91.ZHANG Hu. Research on tooth flank error theory and correction methods for CNC gear profile grinding[D]. Nanjing: Nanjing University of Technology. College of Mechanical and Power Engineering, 2014: 81−91.

[16] 王时龙, 杨勇, 周杰, 等. 大型数控滚齿机热误差补偿建模[J]. 中南大学学报(自然科学版), 2011, 42(10): 3067−3072. WANG Shilong, YANG Yong, ZHOU Jie, et al. Modeling of thermal error compensation of large-scale numerical control gear hobbing machine[J]. Journal of Central South University (Science and Technology), 2011, 42(10): 3067−3072.

[17] 郭秀娟, 袁月, 范小鸥. 模糊聚类算法分析及应用[J]. 吉林建筑工程学院学报, 2009, 26(4): 79−81. GUO Xiujuan, Yuan Yue, FAN Xiaoou. Analysis and application of fuzzy clustering algorithm[J]. Journal of Jilin Institute Architecture & Civil, 2009, 26(4): 79−81.

[18] 王时龙, 祁鹏, 周杰, 等. 数控滚齿机热变形误差分析与补偿新方法[J]. 重庆大学学报, 2011, 34(3): 13−17. WANG Shilong, QI Peng, ZHOU Jie, et al. Thermal deformation error analysis and a novel compensation method for NC gear hobbing machine tools[J]. Journal of Chongqing University, 2011, 34(3): 13−17.

(编辑 伍锦花)

Modeling and compensation of thermal error for large-scale CNC gear profile grinding machine tools

ZHOU Baocang1, WANG Shilong1, FANG Chenggang2, YANG Yong3

(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;2. School of Mechanical and Power Engineering, Nanjing University of Technology, Nanjing 210009, China;3. Chongqing Machine Tool (Group) Co. Ltd., Chongqing 401336, China)

Considering that the thermal error of large-scale computerized numerical control (CNC) gear profile grinding machine tools is an importantfactor for gear machining accuracy, a thermal error experiment platform was established to investigate the relationship between radial thermal error and temperature of the grinding wheel and the workpiece shaft. Then the thermal error compensation models of them were set up by adopting the methods of fuzzy clustering and least-square. After that, the results of thermal error compensation models and the experimental data were compared. The accuracy and reliability of the thermal error compensation models were verified, and the relationship between the thermal error and the temperature of the gear grinding machine tools was also revealed. The results show that the relative errors between models calculation and experimental data are less than 2.000%, and the machining accuracy of tooth surface can be effectively improved more than three levels according to the ISO standard. The analysis indicates the thermal error models have high compensation precision and good reliability.

CNC gear profile grinding machine tools; thermal error; fuzzy clustering; least-square method; error compensation model

10.11817/j.issn.1672−7207.2017.10.016

TH161

A

1672−7207(2017)10−2672−06

2016−12−29；

修回日期：2017−02−06

国家自然科学基金面上项目(51375508)；“十二五”国家科技支撑计划项目(2014BAF08B02)；重庆市杰出青年科学基金项目(cstc2014jcyjjq70001)(Project(51375508) supported by the General Program of National Natural Science Foundation of China; Project(2014BAF08B02) supported by the National Science and Technology Pillar Program during the 12th “Five-year” Plan Period of China; Project (cstc2014jcyjjq70001) supported by the Chongqing Science Funds for Distinguished Young Scholar)

王时龙，博士，教授，博士生导师，从事制造信息自动化、数控装备技术等研究；E-mail：slwang@cqu.edu.cn