太阳影子定位技术的数学原理及其应用

卢 鹏 ，张兴元 ，徐昌贵

（1.西南交通大学峨眉校区基础课部，四川峨眉614202；2.西南交通大学数学学院，四川成都610031）

太阳影子定位技术的数学原理及其应用

卢 鹏1，2，张兴元1，2，徐昌贵1，2

（1.西南交通大学峨眉校区基础课部，四川峨眉614202；2.西南交通大学数学学院，四川成都610031）

利用已有的天文学公式，推导建立了太阳影长与经度、纬度、日期、高度的数学模型.通过在不同时刻测量太阳影子端点处的多组坐标数据，运用最小二乘法原理反解模型，得到了直杆所在位置，以及测量日期.并用给定数据进行检验，得到了模型的正确性与可行性.

影长；高度角；经度；纬度；最小二乘法

如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面，太阳影子定位技术就是通过分析视频中物体的影子变化，确定视频拍摄地点和日期的一种方法.现根据某固定直杆（高度未知）在水平地面上的太阳影子顶点坐标数据（坐标系未知），建立数学模型确定直杆所处的地点和日期.并将模型应用于影子顶点坐标数据.

1 问题分析

物体影子长度变化的参数分别有平太阳时、时角、赤纬角、太阳高度角、当地经度、当地纬度、日期、物体高度等，通过天文学知识将其进行整理，并建立影子长度数学模型.以物体（本文用直杆）为坐标原点建立平面直角坐标系，测量不同时刻时影子端点处的坐标，通过反解模型求出直杆所在位置与日期.

2 影子定位模型的建立

2.1 参数方程模型的建立

2.1 .1 北京时间与当时实际时间，即平太阳时存在偏差，所以需要对数据进行处理，把给出时间化为平太阳时.根据地球自转一周365°，时长24 h，即地球角速度为15°/h，推得平太阳时计算公式［1］为：

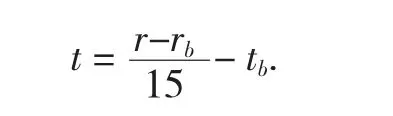
其中：r-当地经度，rb-东经120°，tb-北京时间.

2.1 .2 时角是以正午12点为0°开始算，每一小时为15°，上午为负下午为正，因此时角的计算公式为：

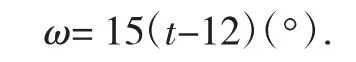
2.1 .3 赤纬角是地球赤道平面与太阳和地球中心的连线之间的夹角.赤纬角不同，表示地球在运行轨道上的位置不同，影响日照范围，即影响影长，其近似计算公式为：

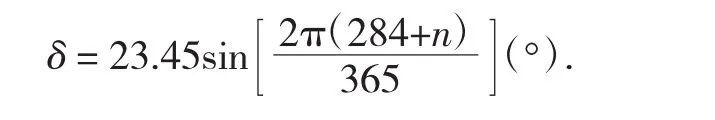
其中：n为日期序号，取值范围为［1,365］的整数；例如：2月8日，则n=39.

2.1 .4 太阳高度角指某地太阳光线与通过该地与地心相连的地表切线的夹角，如图1所示.当太阳高度角为90°时，此时太阳辐射强度最大；当太阳斜射地面时，太阳辐射强度就小［2-3］.其近似计算公式为：

其中：φ为当地纬度.

2.1.5 太阳方位角即太阳所在的方位，指太阳光线在地平面上的投影与当地经线的夹角，可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角，如图1所示.其近似计算公式为：

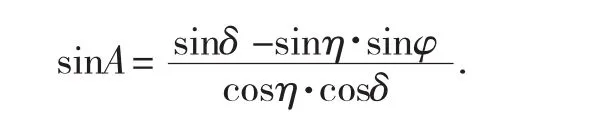
2.2 坐标转换模型的建立

本文中以直杆坐标为原点，建立了测量直杆影子坐标的直角坐标系［4］，但不能确定正北方向就为y轴正向，为了解决这个问题进行坐标变化，可以等到原坐标系与新坐标系（正北方向为y轴正向，如图2所示）之间的关系：

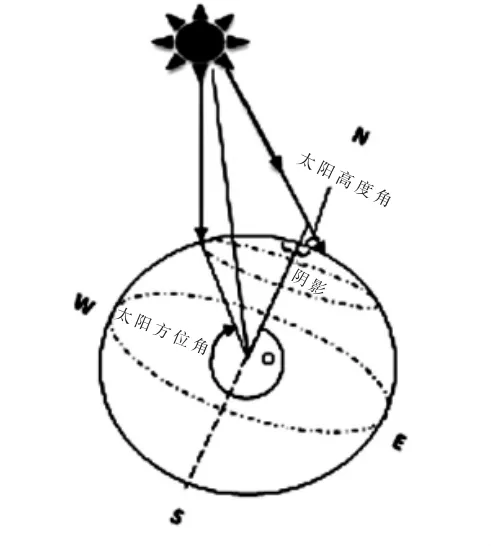
图1 高度角与方位角示意图

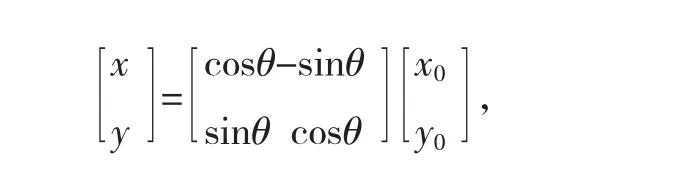
其中：x0，y0表示直杆影子坐标系；x，y表示y轴为正北方向的坐标系.

2.3 影子定位模型的建立

地球是半径约为6 731 km的近似球体，表面曲度小，在一定范围内可近似看做平面，由图3可得到影子在地平面上长度L、直杆长h和太阳高度角η间的关系：

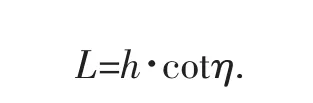
由以上公式合并化简带入，可得影长与经度、纬度、日期、高度的最终函数表达式：

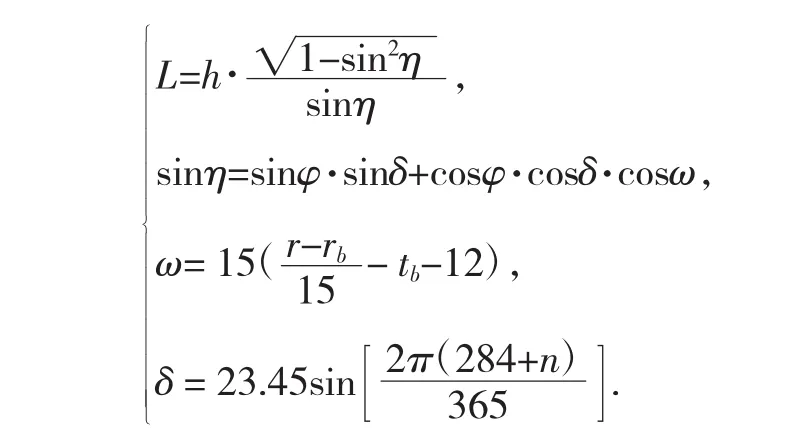
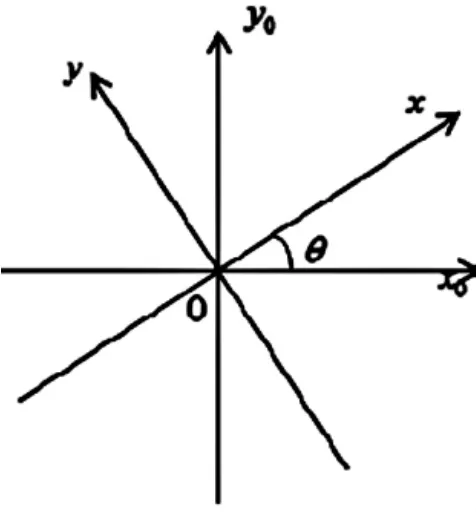
图2 坐标转换示意图

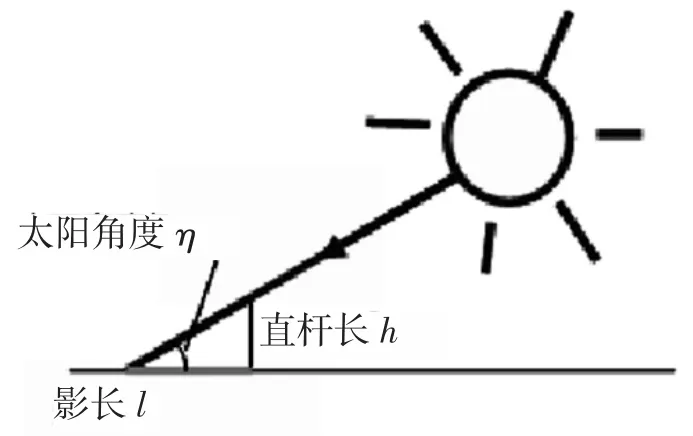
图3 太阳高度角与直杆的关系

其中：常数rb=120°，tb北京时间；变量经度r，纬度φ，日期n，高度h.

3 模型的求解

现有两组数据，如表1所示，需要求解非线性方程组得出杆所在的位置与日期.因为坐标系的旋转不会影响影子长度变化，即，从而可采用以目标函数为的优化模型进行求解，即用非线性最小二乘法拟合［5-7］求出模型中的未知变量，如：经度、纬度、日期和高度.

计算 MATLAB 程序［9］如下：

定义fun函数（下述代码另存为工作目录下的fun.m文件）：

function f=fun(k,t)

Lb=120;ga=23.45*sin(2*pi*(284+k(4))/365);

f=k(1)*cotd(abs(asind(sind(k(2))*sind(ga)+cosd(k(2))*cosd(ga)*cosd(k(3)-Lb-12*15+15*t))));

主程序：

T= [761/60 764/60 767/60 770/60 773/60 776/60 779/60 782/60 785/60 788/60 791/60 794/60 797/60 800/60 803/60 806/60 809/60 812/60 815/60 818/60 821/60;

-1.235 2-1.208 1-1.181 3-1.154 6-1.128 1-1.101 8-1.075 6-1.049 6-1.023 7-0.998-0.972 4-0.947-0.921 7-0.896 5-0.871 4-0.846 4-0.821 5-0.796 7-0.771 9-0.747 3-0.722 7;

0.1 73 0.189 0.204 8 0.220 3 0.235 6 0.250 5 0.265 3 0.279 8 0.294 0.308 0.321 8 0.335 4 0.348 8 0.361 9 0.374 8 0.387 6 0.400 1 0.412 4 0.424 6 0.436 6 0.448 4]';

t=T(:,1);x=T(:,2);y=T(:,3);

L=sqrt(x.^2+y.^2);

k0=[3 50 100 300];

[k,fval]=lsqcurvefit('fun',k0,t,L)

程序结果：

k=2.000 8 39.892 6 79.743 8 200.344 9；

fval=1.682 8e-008.

4 模型的分析与验证

从上述结果可以看出，采用非线性拟合求出的参数误差非常小，准确性高；此方法可以作为未知日期情况下，求解影子位置的模型.但迭代初值的选取会影响最终的结果，所以答案不是唯一的，一般情况下有几个位置及日期的选择方案，表2给出了具体的检验数据，用本文提供的模型和算法进行验证.

将上述数据带入Matlab软件中计算可得三组结果，如表3所示.

从表3可以看出，每次结果经度纬度误差不大，但是日期变化剧烈，所以模型对于定位还是有不错的效果，但是定日效果一般，如果对日期有特别的要求，必须对模型进行改进，方能使用.

5 模型的评价

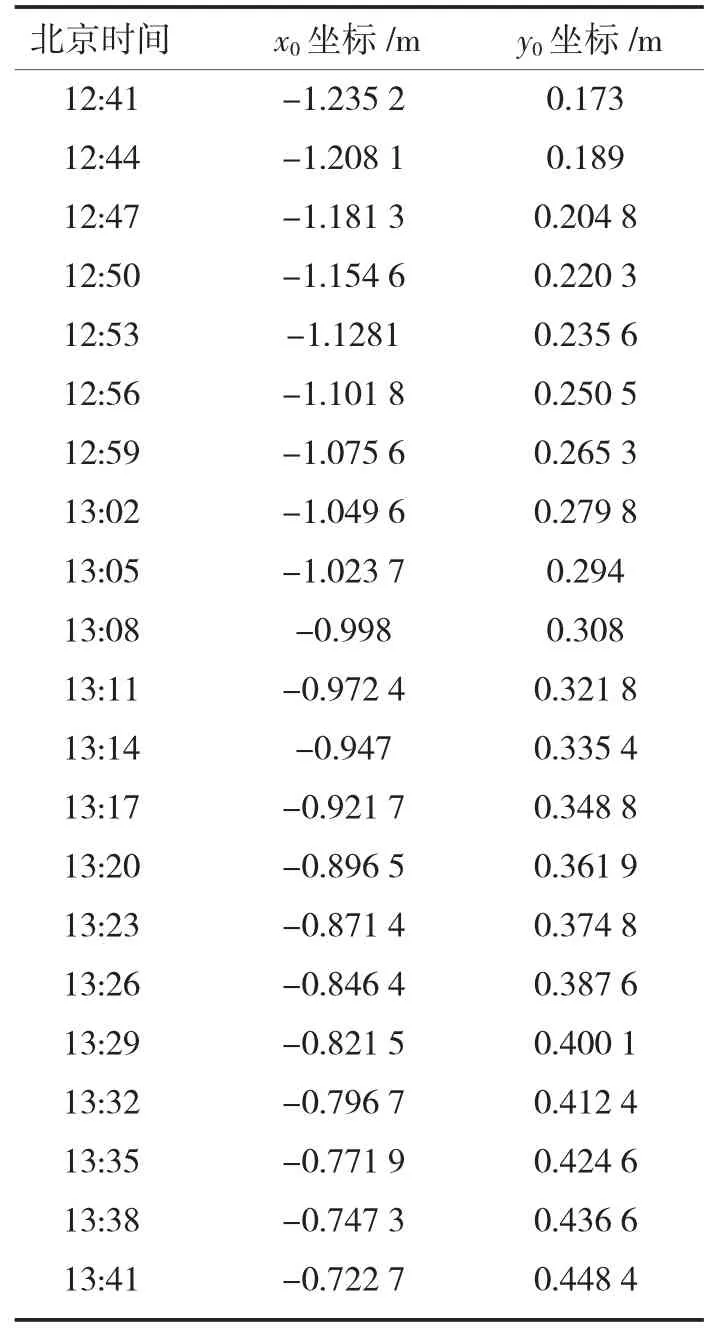
表1 时间与坐标测量值

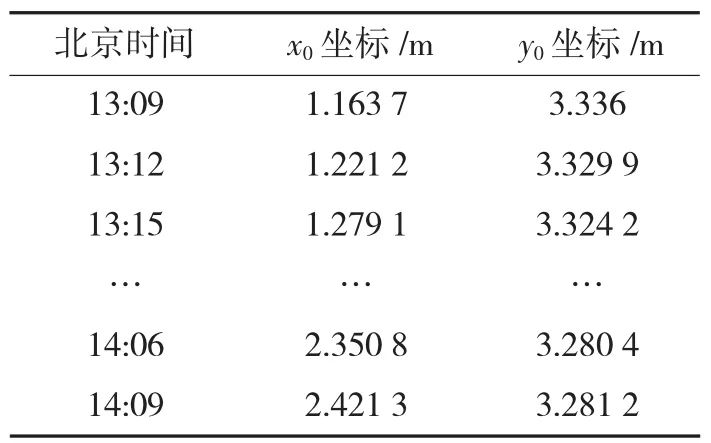
表2 检验数据

5.1 模型的优点

利用成熟的天文学公式建立的模型结构精简，计算快捷，定位效果尚佳.求解时并未采用坐标直接进行最小二乘拟合，关键在于坐标系建立方向未知，强行使用必然多了一个求解参数，势必增加了求解的难度，从而运用影子长度拟合计算避开了关于坐标系方向未知的影响.在实际应用时，不需要建立坐标系，只需测量出几组不同时间的影子长度，就可以根据模型得出此位置和日期，非常方便.

表3 迭代初值(高度,纬度,经度,日期)及结果

5.2 模型的缺点

因为模型中关于高度角是近似公式，拟和函数存在着一定的偏差，导致结果与实际情况存在一定的误差.计算时采用的是非线性拟合求出了局部最优解（依赖于初值），更好的是得出全局最优解.

5.3 模型的进一步改进

当直杆长度未知时，可利用相邻两个时间点的影子长度相除即可消去直杆长度.这样在进行求解时，方程的个数没有少，而参数少一，则能更快，更精确地得到最后的结果，也能提高此模型的定日效果.求解模型时还可以采用变步长搜索法，即先用较大的步长进行粗略搜索，在其中几组最优解附近减小步长进行精确搜索.重复这一过程，直到达到事先设定的精度为止，这样大大的减少了搜索时间，提高了搜索的效率.如果数据量比较多时，还可以留下几组数据用来对模型进行检测.

本文利用已有的天文学公式，推导建立了关于影长与经度、纬度、日期、高度的数学模型，通过建立坐标系，测量多个时刻的太阳影子坐标，运用最小二乘法原理，反解模型得到物体所在位置及日期.通过给定数据检验，说明了模型的正确性和可行性.

［1］谈小生,葛成辉.太阳角的计算方法及其在遥感中的应用[J].国土资源遥感,1995（2）：48-57.

［2］Averill M Law.仿真建模与分析[M].4版.肖田元，范文慧，译.北京：清华大学出版社，2012.

［3］贺晓雷,于贺军,李建英,等.太阳方位角的公式求解及其应用[J].太阳能学报，2008，29（1）：69-70.

［4］孟道骥.高等代数与解析几何：上下册[M].北京：科学出版社，2007.

［5］姜启源,谢金星,叶俊.《数学模型》[M].4版.北京：高等教育出版社，2010.

［6］司守奎,孙玺清.数学建模算法与应用[M].2版.北京：国防工业出版社,2015.

［7］韩忠庚.数学建模方法及其应用[M].2版.北京：高等教育出版社,2009.

［8］刘易成,蔡志杰.2015年高教社杯全国大学生数学建模竞赛A题[M].北京：国防工业出版社,2012.

［9］栾颖.MATLAB R2013a基础与可视化编程[M].北京：清华出版社，2014.

The Mathematical Principles and Applications of Sun Shadow Positioning Technology

LU Peng1,2,ZHANG Xing-yuan1,2,XU Chang-gui1,2
（1.Emei Campus,Southwest Jiaotong University,Emei 614202,Sichuan,China;2.College of Mathematics,Southwest Jiaotong University,Chengdu 610031,Sichuan,China）

In this paper,the existing astronomical formulas derived to establish a long shadow with latitude,longitude,date,highly mathematical model.By measuring the sun shadow of the endpoint at different times multiple sets of coordinate data,the principle of least square method of inverse solution model,we got the straight bar for the location,as well as the measurement date.And with the given data to test,we got the correctness and feasibility of the model.

shade length；elevation angle；longitude；latitude；least square method

O29

A

1007-5348（2017）09-0015-04

2017-06-21

中央高校基本科研业务费专项资金（2682014BR039）.

卢鹏（1983-），男，四川自贡人，西南交通大学基础课部讲师，硕士；研究方向：数学建模与粗糙集.

（责任编辑：邵晓军）