非对称纳米通道内流体流动与传热的分子动力学∗

王胜 徐进良 张龙艳

(华北电力大学,低品位能源多相流与传热北京市重点实验室,北京 102206)

非对称纳米通道内流体流动与传热的分子动力学∗

王胜 徐进良†张龙艳

(华北电力大学,低品位能源多相流与传热北京市重点实验室,北京 102206)

非对称浸润性,速度滑移,温度阶跃,粗糙纳米通道

采用分子动力学方法研究了流体在非对称浸润性粗糙纳米通道内的流动与传热过程,分析了两侧壁面浸润性不对称对流体速度滑移和温度阶跃的影响,以及非对称浸润性组合对流体内部热量传递的影响.研究结果表明,纳米通道主流区域的流体速度在外力作用下呈抛物线分布,但是纳米通道上下壁面浸润性不对称导致速度分布不呈中心对称,同时通道壁面的纳米结构也会限制流体的流动.流体在流动过程中产生黏性耗散,使流体温度升高.增强冷壁面的疏水性对近热壁面区域的流体速度几乎没有影响,滑移速度和滑移长度基本不变,始终为锁定边界,但是会导致近冷壁面区域的流体速度逐渐增大,对应的滑移速度和滑移长度随之增大.此时,近冷壁面区域的流体温度逐渐超过近热壁面区域的流体温度,流体出现反转温度分布,流体内部热流逆向传递.随着两侧壁面浸润性不对称程度增加,流体反转温度分布更加明显.

1 引 言

近年来,纳米通道内流体的流动与传热规律受到人们越来越多的重视.在微纳系统中,物质输运和能量传递均发生在一个受限的微小空间内,微纳尺度效应导致界面上出现了许多不同于常规尺度的现象.液体在纳米通道中流动时,固液界面处会出现速度滑移现象.Nagayama和Cheng[1]及Zhang等[2]对纳米通道内的Poiseuille流动进行了研究,发现壁面浸润性和驱动力会影响固液界面边界条件.当固液相互作用较弱时,在界面处将会出现很明显的速度滑移,随着固液相互作用增大,速度滑移不断减小.曹炳阳等[3,4]对纳米通道内的Couette流动进行了研究,发现界面上的滑移速度随着液体与固体表面势能作用的增强而减小.固体表面润湿性不同,固液边界可能发生滑移、无滑移与负滑移等现象.徐超等[5]发现,流体温度以及壁面吸引力强度对滑移速度影响较大.壁面吸引力不同,流体温度对密度分布的影响规律不同,从而导致对滑移速度的影响规律也不一致.

流体在纳米通道中的传热过程也存在类似界面现象,在界面上会出现温度阶跃.从微观角度而言,认为这种界面现象的产生是因为界面两侧的材料在电子或者声子输运方面的性质不同,界面上的能量传递主要依靠载热子,一般材料中的载热子为电子或者声子.界面两侧材料的输运性质不同,携带能量的载热子在穿过界面时会发生散射,无法全部穿过界面,相当于界面阻碍了热量输运,温度分布出现阶跃.近年来,众多学者纷纷采用分子动力学方法对界面温度阶跃现象展开研究.Kim等[6,7]发现界面上的温度阶跃不仅受固液之间相互作用强度影响,还依赖于墙体的刚度.当固液相互作用较强时,界面传热得到强化,从而使界面热阻降低.墙体刚度越大,界面热阻越大.Barisik和Beskok[8]在研究水硅界面热阻时发现,当固液相互作用较强时,硅壁面温度不仅影响界面处的声子传输,还影响近壁面处水的密度分布,界面热阻随着壁面温度升高而增加;当固液相互作用较弱时,壁面温度不影响近壁面处水的密度分布,热阻长度随着壁面温度升高而减小.

实际上,固体表面即使在原子尺度下也不可能是完全光滑的,表面粗糙度分布直接影响固液界面处的速度滑移和温度阶跃[9].Yang[10]发现表面粗糙度会抑制固液界面处的速度滑移.相比于光滑表面,阻力的增加会导致粗糙表面上呈现无滑移或者锁定边界现象.Zhang和Chen[11]在研究Couette流动的过程中发现,相比于光滑表面,无论流体横向或纵向流动,粗糙表面都会额外损失能量,导致界面速度减小.壁面粗糙度增加时,近壁面区域流体流动更加不规则,速度滑移长度逐渐减小.Wang和Keblinski[12]分析了壁面浸润性和表面粗糙度对固液界面上传热的影响,结果表明,粗糙表面的亲疏水性发生转换时,界面热阻会出现突变.

固液界面处的速度滑移与温度阶跃都是十分重要的界面现象,多数情况下在界面输运过程中都是单独考虑,很少涉及流动与传热之间的耦合,因此对速度滑移与温度阶跃进行耦合模拟具有重要意义.Sun等[13,14]发现滑移长度与热阻长度之间的关系与壁面浸润性有关.当固液相互作用力较弱时,热阻长度随滑移长度单调增加,当固液相互作用较强时,热阻长度不随滑移长度变化.张程宾等[15]主要研究了粗糙表面对流体流动与传热过程的影响,发现表面粗糙度的存在使得流体剪切流动产生了额外的黏性耗散,使粗糙纳米通道内的流体速度小于光滑通道,温度水平高于光滑通道,并且粗糙表面的速度滑移与温度阶跃均小于光滑表面.

综上所述,目前研究流动换热规律的纳米通道都是对称系统,如纳米通道上下壁面浸润性或温度相同等.仿生学领域的研究引起学者对非对称功能性材料的广泛关注[16,17],尤其是不对称系统所产生的异常行为[18,19].本文建立液体在两侧壁面浸润性不对称的粗糙纳米通道内流动的分子动力学模型,研究了两侧壁面浸润性不对称对流体速度分布、温度分布、速度滑移、温度阶跃以及流体内热流的影响,分析不同浸润性组合的粗糙纳米通道内流体的流动换热耦合规律,特别是流体内部热流的变化.模拟采用开源分子动力学模拟软件LAMMPS实现,原子位型可视化采用OVITA软件实现.

2 物理模型及模拟细节

模拟的纳米通道内液体流动的分子动力学模型如图1(a)所示.模拟体系的尺寸为Lx×Ly×Lz=17.15σ×11.3σ×21.2σ,液体处于两块平行固体壁面之间.上下固体壁面均存在纳米结构,壁面之间的间距H为16σ.通过给每个液体原子施加平行于平板的驱动力F,促使液体沿x方向流动,类似于在重力作用下的流动.整个模拟体系在x,y方向上施加周期性边界条件,z方向上为固定边界条件.

液体氩原子之间的相互作用采用Lennard-Jones(LJ)势能模型,表达式为

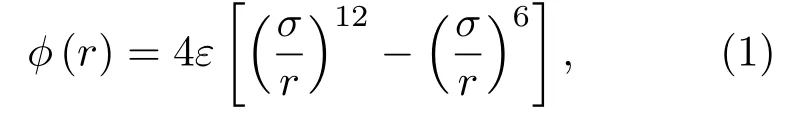
图1 (网刊彩色)(a)模拟系统图;(b)纳米结构示意图Fig.1.(color online)(a)Simulation system;(b)schematic of nanostructure.

式中r为原子间的距离,σ为尺寸参数,ε为能量参数.液体氩原子之间的尺寸参数σ=0.3405 nm,能量参数ε=1.670×10−21J,原子质量m=6.69×10−23g.固体原子之间的相互作用也采用LJ势能模型,此时固体原子之间的尺寸参数σs=0.73σ=0.2475 nm,能量参数εs=50ε=8.35×10−20J,忽略电子之间的相互作用力.至于固体和液体之间的相互作用力,需要对LJ势能模型进行修正,

根据Lorentz-Berthelot混合规则,固液原子之间的尺寸参数σsl=(σ+σs)/2,能量参数和β为势能系数,改变系数α和β可以改变固体与液体之间的相互作用力.热壁面设为亲水性表面,势能系数α=0.14,β=1.0.冷壁面的势能系数α=0.14,通过冷壁面势能系数β分别取0.1,0.2,0.3,0.4,0.5,0.6来研究两侧壁面浸润性不对称对通道中流体速度滑移和温度阶跃的影响.势能系数β越大,壁面亲水性越强,疏水性越弱[1].为减少计算量,取截断半径rc=2.5σ,对于距离超过2.5σ的原子,其相互作用忽略不计.

模拟过程中,液体原子按照面心立方结构(FCC)排列, 密度设为ρlσ3=0.78,对应的晶格常数为1.72σ.壁面原子也按照 FCC排列,并使其 (111)晶面与流体原子相接触,壁面密度设为ρs=3.35ρl,其中ρl为液体数密度. 如图1(a)所示,壁面每一侧有8层固体原子,靠近流体区域的4层固体原子构成热浴原子,与流体区域进行热量传递.为控制壁面的温度,壁面最外层布置4层虚拟原子,以模拟其无限大势场.虚拟原子仍按照(111)晶面排布,最外层虚拟原子为固定原子,运行过程中使原子固定在晶格位置处静止不动,以便维持整个系统的稳定.冷壁面和热壁面存在的纳米结构如图1(b)所示,纳米结构宽度b为3.261σ,高度h为2.658σ,对应位置之间的距离s为5.706σ.固体壁面原子通过弹簧力束缚在初始位置,弹簧系数的大小反映了固体壁面原子热振动程度[20].

采用Velocity-Verlet算法求解运动方程,时间步长取为Δt=0.001τ,其中τ=(mσ2ε−1)1/2为LJ约化时间常数.首先,采用正则系综(NVT)控制整个系统温度T=0.827ε/kB,模拟系统达到平衡状态时,所有流体原子速度遵循高斯分布.采用Langevin热浴控制冷壁面温度T=0.827ε/kB,热壁面温度T=0.992ε/kB,对液体沿x方向施加驱动力F=0.02ε/σ驱动其在通道内形成流动,达到稳定后统计相关结果.

模拟中为了统计纳米通道中各个物理参数,将沿z方向且平行于xy平面的流体计算区域分为n层.则在第JP—JQ个时间段内,第k层(1≤k≤n)区域流体的粒子密度为

式中Nk为第k层液体区域粒子数目,Δz为各液体分层的厚度,A为液体计算区域在x,y方向上的面积,A=Lx×Ly.

在第JP—JQ个时间段内,第k层(1≤k≤n)区域流体沿x方向的平均速度为

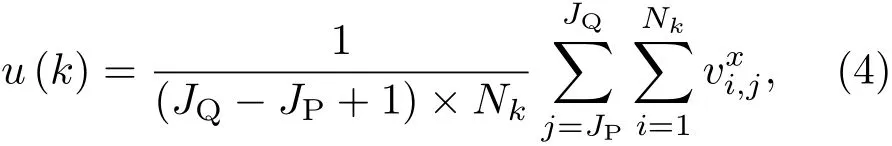
式中为粒子i在j时间步沿x方向的速度.

在第JP—JQ个时间段内,第k层(1≤k≤n)区域流体的温度为

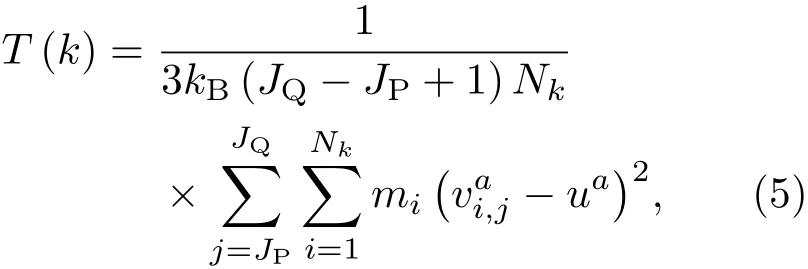
式中a代表x,y和z三个方向,在稳定状态下uy和uz为0.

流体区域的热流密度计算公式为

式中Ω为流体体积;N为流体原子数目;ei为原子i的总能量,包括动能和势能;Fij为原子i与原子j之间的相互作用力;vi为原子i的速度;rij为原子i与原子j之间的距离.整个模拟过程中统计热流时,会存在波动.

固液界面处的滑移规律可以由滑移长度ls描述,计算公式为

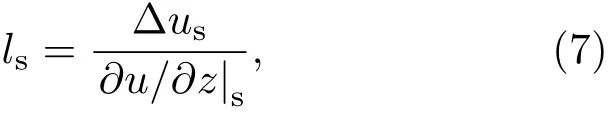
式中Δus为固液界面处的滑移速度,∂u/∂z|s为固液界面处流体的速度梯度.ls＞0为滑移边界条件;ls=0为无滑移边界条件;ls＜0为锁定边界条件.

类似于速度滑移长度的定义,温度阶跃长度lK可定义为

式中ΔT为固液界面处的温度阶跃,∂T/∂z|s为固液界面处流体的温度梯度.如果固体壁面存在纳米结构,则假定固液之间的理论界面处于纳米结构的中心线位置.

3 结果与讨论

3.1 密度分布

图2所示为纳米通道内流体沿z方向的密度分布,横坐标表示沿z方向的高度,长度单位为σ,纵坐标为无量纲数密度ρ∗=ρσ3,可以直观地显示纳米通道内流体分布的微观特征.图中两侧淡灰色部分表示壁面纳米结构,虚线表示固液之间的理论界面.固体与液体之间势能作用的影响域为纳米量级,因此固体只影响流体原子在近壁面区域的分布特性.图2结果显示,近壁面区域流体密度分布出现明显的振荡现象,表明该区域的流体产生了分层,密度是不均匀的.在通道中心的主流区域,流体受固体壁面的影响较小,密度分布趋近于一致,仅在恒定值附近小幅度波动.热壁面与冷壁面的浸润性不一致,将会导致纳米通道内流体密度分布不对称.且近热壁面区域流体密度分布的波动幅度比近冷壁面区域的流体密度分布波动幅度大.保持热壁面亲水性不变,通过改变冷壁面的势能系数β来改变冷壁面的浸润性.结果发现,由于势能作用的影响范围较小,冷壁面浸润性的变化基本不影响近热壁面区域流体的密度分布.但是对于近冷壁面区域的流体而言,随着势能系数β的增大,流体密度分布的波动幅度明显增大,而且各分层波峰的位置逐渐向壁面方向发生偏移.这是因为随着势能系数β的增大,固液之间的相互作用力增强,越靠近壁面的流体原子越容易被束缚,从而无法自由移动,该区域的流体密度增加,引起各分层波峰位置更加靠近壁面.

图2 (网刊彩色)不同冷壁面势能系数β下流体沿z方向的密度分布Fig.2.(color online)Density pro fi les in the z-direction with different cold interface coefficient β.

3.2 速度分布和温度分布

纳米通道表面纳米结构和浸润性会改变近壁面区域内流体的密度分布,对受限空间内流体的流动换热过程具有显著的影响.图3(a)纵坐标为无量纲速度u∗=uτ/σ,表示纳米通道中流体沿z方向的速度分布,图3(b)表示纳米通道中冷热壁面处固液界面滑移速度随冷壁面势能系数β的变化规律.图3(a)结果显示,在纳米通道中心的主流区域,流体的速度呈抛物线分布,但是热壁面与冷壁面的浸润性不一致,导致流体的速度分布不呈中心对称.图中淡灰色表示纳米通道壁面的纳米结构,虚线为固液之间的理论界面.表面的粗糙结构将阻碍流体原子的流动,使流体难以从粗糙结构槽中进入主流区域,因此可以发现,粗糙结构槽深处的流体速度几乎为零.热壁面呈现亲水性,固体将会束缚近热壁面区域的流体原子,同时壁面纳米结构阻碍流体原子流动,导致该区域流体速度相对较小,冷壁面的浸润性发生变化基本不影响近热壁面区域的流体速度分布,因此热壁面侧的滑移速度保持不变.冷壁面呈现疏水性,固体对液体的约束能力相对较弱,存在速度滑移,而且随着冷壁面势能系数β的增加,冷壁面的疏水性逐渐减弱，向亲水性转变,近冷壁面区域流体速度逐渐下降,滑移速度也随之下降.

外力驱动流体在纳米通道内流动,流体与流体之间的剪切作用和界面处流体与固体之间的摩擦作用都会引起黏性耗散,产生的热量将导致纳米通道内流体的温度升高,甚至超过两侧壁面温度,这些热量将通过界面向壁面处传递.

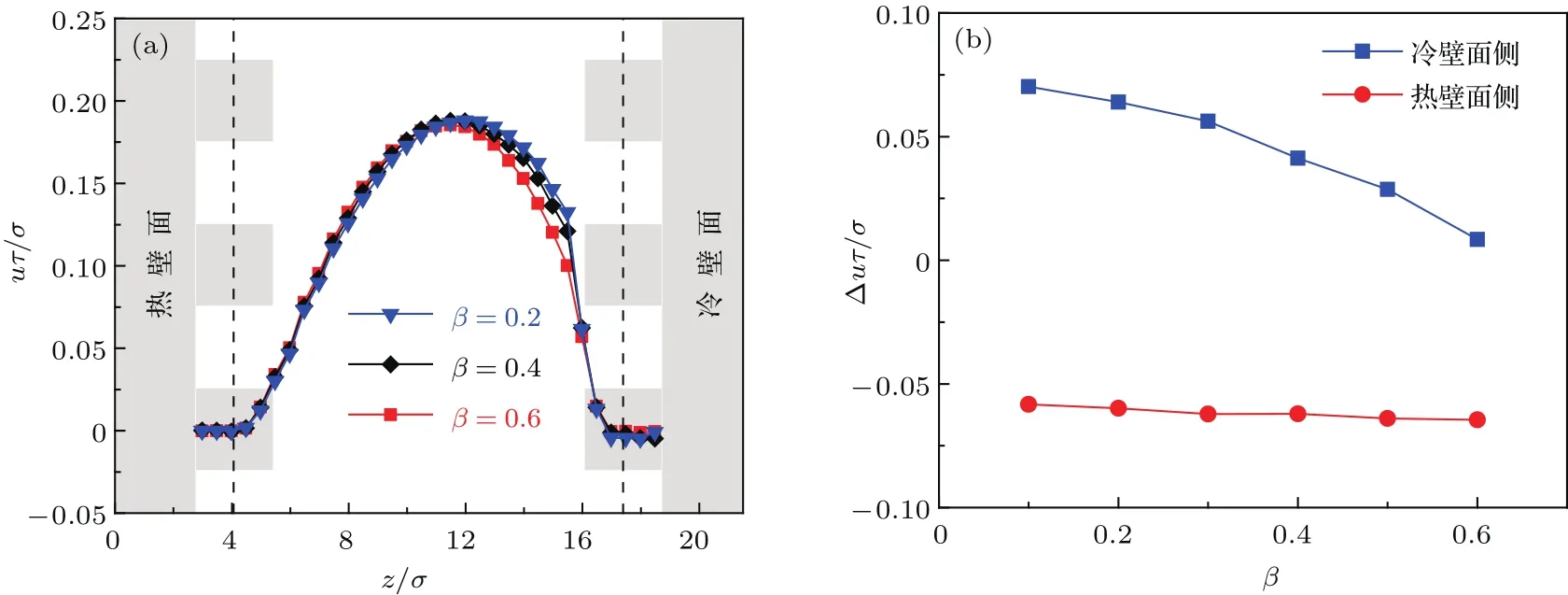
图3 (网刊彩色)(a)不同冷壁面势能系数β下流体沿z方向的速度分布;(b)界面滑移速度受冷壁面势能系数β的影响Fig.3.(color online)(a)Velocity pro fi les in the z-direction with different cold interface coefficient β;(b)e ff ect of cold interface coefficient β on the slip velocity.

图4 (网刊彩色)(a)不同冷壁面势能系数β下流体沿z方向的温度分布;(b)界面阶跃温度受冷壁面势能系数β的影响Fig.4.(color online)(a)Temperature pro fi les in the z-direction with different cold interface coefficient β;(b)e ff ect of cold interface coefficient β on the jump temperature.

图4(a)中纵坐标为无量纲温度T∗=TkB/ε,表示纳米通道内流体沿z方向的温度分布,图4(b)给出了界面阶跃温度随冷壁面势能系数β的变化规律.从图4(a)可以看出,随着冷壁面势能系数β减小,冷壁面浸润性减弱,近冷壁面区域流体的滑移速度增大,剪切作用所产生的热量增加.同时,增强冷壁面疏水性将会阻碍固体与液体之间的能量传递,黏性耗散所产生的热量难以从该界面处传递到壁面,因此纳米通道内流体的温度升高.随着冷壁面势能系数β变化,纳米通道内流体的温度分布出现反转现象,即近冷壁面区域的流体温度高于近热壁面区域的流体温度.这是因为当冷壁面势能系数β较小时,冷壁面疏水性较强,界面热阻相对较大,阻碍了热量的传递,从而导致近冷壁面区域的流体温度大幅度升高,最终超过近热壁面区域的流体温度.正如图4(b)所示,热壁面侧的界面阶跃温度相对较小,冷壁面侧的界面阶跃温度相对较大.随着冷壁面势能系数β的减小,两侧的界面阶跃温度逐渐增大,但是冷壁面的温度阶跃上升幅度相对较大,从而导致该区域的流体温度逐渐超过近热壁面区域流体的温度.

3.3 速度滑移和温度阶跃

固液相互作用强度决定了固体与液体之间的相互作用,从而影响界面上的动量和能量传递,图5给出了粗糙纳米通道中的速度滑移长度ls和温度阶跃长度lK随冷壁面势能系数β的变化规律,其纵坐标单位均为σ.从图5(a)可以看出,近热壁面区域流体的速度滑移长度基本不变,正如之前所说,冷壁面浸润性的变化不影响近热壁面区域的流体速度分布,而且速度滑移长度为负值,说明热壁面侧处于锁定边界条件.冷壁面呈疏水性,固体对液体的约束能力相对较弱,速度滑移长度相对较大,而且速度滑移长度为正值,说明冷壁面处于滑移边界条件.随着冷壁面势能系数β的增加,壁面亲水性增强,固液之间的动量和能量交换更加频繁,从而减小了界面上的不连续程度,界面处的速度滑移长度随之单调减小.从图5(b)可以发现,冷壁面浸润性的变化对两侧固液界面处的温度阶跃长度都有影响.随着冷壁面势能系数β的增加,温度阶跃长度逐渐增大,然后减小,存在极大值,极大值对应于图4(a)中主流区域流体温度分布趋于一致的情况.图6所示为流体热流随冷壁面势能系数β的变化关系,纵坐标为无量纲热流q∗=qm1/2σ3/ε3/2.当冷壁面势能系数β较小时,流体热流沿z轴负方向传递;当冷壁面势能系数β较大时,流体热流沿z轴正方向传递.随着冷壁面势能系数β的减小,流体内热流出现正向传递到负向传递的转变，相应的流体温度分布出现反转现象.

图5 流体的(a)速度滑移长度和(b)温度阶跃长度受冷壁面势能系数β的影响Fig.5.E ff ect of cold interface coefficient β on(a)velocity slip length and(b)temperature jump length.

图6 流体的热流受冷壁面势能系数β的影响Fig.6.E ff ect of cold interface coefficient β on heat flux of the fl uid.

4 结 论

本文采用分子动力学方法研究了非对称浸润性的粗糙纳米通道内流体的流动换热过程,探讨了两侧壁面浸润性不对称程度对流体速度滑移和温度阶跃的影响,以及不对称浸润性组合对流体内部热流传递的影响,得到如下结论.

1)在驱动力的作用下,主流区域流体的速度沿着z方向呈现抛物线分布,但是两侧壁面浸润性不对称导致速度分布不呈中心对称.流体在靠近不同浸润性壁面处的密度分布出现明显差异.靠近亲水壁面处,固液相互作用强,密度波动幅度大,流体原子分布密集;靠近疏水壁面处,固液相互作用弱,流体密度波动幅度小,流体原子分布稀疏,这种密度分布的差异性将会影响流体的流动.流体在流动过程中会产生黏性耗散,流体温度升高,甚至会超过两侧壁面温度.

2)壁面浸润性对速度滑移和温度阶跃有十分重要的影响.增强冷壁面的疏水性对近热壁面区域的流体速度几乎没有影响,滑移速度和滑移长度基本不变,始终呈现锁定边界,但是会导致近冷壁面区域的流体速度逐渐增大,对应的滑移速度和滑移长度随之增大.同时,两壁面的温度阶跃随着冷壁面亲水性增强而逐渐减小,但是冷壁面的界面温度阶跃幅度大于热壁面,导致近冷壁面区域的流体温度逐渐超过近热壁面区域的流体温度,流体出现反转温度分布,流体内部热流逆向传递.随着两侧壁面浸润性不对称程度增加,反转温度分布更加明显.

[1]Nagayama G,Cheng P 2004Int.J.Heat Mass Transfer47 501

[2]Zhang H W,Zhang Z Q,Ye H F 2012Micro fl uid.Nano fl uid.12 107

[3]Cao B Y,Chen M,Guo Z Y 2006Acta Phys.Sin.55 5305(in Chinese)[曹炳阳,陈民,过增元 2006物理学报55 5305]

[4]Cao B Y,Chen M,Guo Z Y 2003J.Eng.Therm.24 670(in Chinese)[曹炳阳,陈民,过增元 2003工程热物理学报24 670]

[5]Xu C,He Y L,Wang Y 2005J.Eng.Therm.26 912(in Chinese)[徐超,何雅玲,王勇2005工程热物理学报26 912]

[6]Kim B H,BeskokA,CaginT 2008Micro fl uid.Nano fl uid.5 551

[7]Kim B H,Beskok A,Cagin T 2008J.Chem.Phys.129 174701

[8]Barisik M,Beskok A 2014Int.J.Therm.Sci.77 47

[9]Cao B Y,Sun J,Chen M,Guo Z Y 2009Int.J.Mol.Sci.10 4638

[10]Yang S C 2006Micro fl uid.Nano fl uid.2 501

[11]Zhang C B,Chen Y P 2014Chem.Eng.Process.85 203

[12]Wang Y,Keblinski P 2011Appl.Phys.Lett.99 073112

[13]Sun J,Wang W,Wang H S 2013J.Chem.Phys.138 234703

[14]Sun J,Wang W,Wang H S 2013Phys.Rev.E87 023020

[15]Zhang C B,Xu Z L,Chen Y P 2014Acta Phys.Sin.63 214706(in Chinese)[张程宾,许兆林,陈永平2014物理学报63 214706]

[16]Zhang X Y,Zhu Y X,Granick S 2002Science295 663

[17]Sun T L,Lin F,Gao X F,Jiang L 2005Acc.Chem.Res.38 644

[18]Chen Q W,Meng L Y,Li Q K,Wang D,Guo W,Shuai Z G,Jiang L 2011Small7 2225

[19]Murad S,Puri I K 2012J.Chem.Phys137 081101

[20]Priezjev N V 2007J.Chem.Phys.127 144708

Molecular dynamics simulation of fl uid fl ow and heat transfer in an asymmetric nanochannel∗

Wang Sheng Xu Jin-Liang†Zhang Long-Yan

(Beijing Key Laboratory of Multiphase Flow and Heat Transfer for Low Grade Energy,North China Electric Power University,Beijing 102206,China)

5 May 2017;revised manuscript

4 June 2017)

Fluid fl ow and heat transfer in a nanochannel may depart from the traditional behavior due to the scale e ff ect,and the velocity slip and temperature jump at the fl uid-solid interface must be taken into account.A lot of papers about fluid flows in nanochannels with the same wettability at two surfaces have been published.It is necessary to investigate fluid flow and heat transfer in nanochannels with the asymmetric wettability by the molecular dynamics method.The fluid velocity and temperature distributions,interfacial velocity slip and temperature jump in a rough nanochannel are evaluated.The e ff ects of asymmetric wettability on the velocity slip,temperature jump and internal fl uid heat transfer are analyzed.The results indicate that the velocity of the fl uid fl ow under an external force in a nanochannel in a bulk region is of a parabolic distribution,but the parabolic distribution is not centrosymmetric because of the centrosymmetric density pro fi le.The di ff erence in density distribution can a ff ect the fl uid fl ow.Viscous dissipation due to shear fl ow will increase the fl uid temperature.The range that is a ff ected by the interaction between solid and liquid is small.So the wettability of the cold wall hardly a ff ects the velocity of the fl uid near the hot wall,and the slip velocity is almost constant.At this time,the negative slip will take place at the fl uid-solid interface near the hot wall.But the velocity of the fl uid near the cold wall comes up with the increasing hydrophobicity of the cold wall,and the slip velocity increases.The temperature jump on both sides of interface increases with the increasing hydrophobicity of the cold wall,but the degree of temperature jump at a liquid-cold solid interface is higher than that at a liquid-hot solid interface.Then the fluid temperature near the cold wall gradually exceeds the fluid temperature near the hot wall.The internal heat flow of the fl uid will be reversed.The inverted temperature pro fi le of the fl uid will appear.The inverted temperature pro fi le becomes more obvious when the degree of asymmetric wettability increases.

asymmetric wettability,velocity slip,temperature jump,rough nanochannel

(2017年5月5日收到;2017年6月4日收到修改稿)

10.7498/aps.66.204704

∗国家自然科学基金(批准号:51436004)资助的课题.

†通信作者.E-mail:xjl@ncepu.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:47.61.–k,68.08.–p,68.35.Ct,02.70.NsDOI:10.7498/aps.66.204704*Project supported by the National Natural Science Foundation of China(Grant No.51436004).†Corresponding author.E-mail:xjl@ncepu.edu.cn