动态突触、神经耦合与时间延迟对神经元发放的影响∗

于文婷 张娟 唐军

(中国矿业大学物理学院,徐州 221116)

动态突触、神经耦合与时间延迟对神经元发放的影响∗

于文婷 张娟 唐军†

(中国矿业大学物理学院,徐州 221116)

神经元,突触刺激,傅里叶变换,延迟

神经元膜电位的受激发放在神经系统的信息传递中起着重要作用.基于一个受动态突触刺激的突触后神经元发放模型,采用数值模拟和傅里叶变换分析的方法研究了动态突触、神经耦合与时间延迟对突触后神经元发放的影响.结果发现:突触前神经元发放频率与Hodgkin-Huxley神经元的固有频率发生共振决定了突触后神经元发放的难易,特定频率范围内的电流刺激有利于神经元激发,动态突触输出的随机突触电流中这些电流刺激所占的比率在很大程度上影响了突触后神经元的发放次数;将突触后神经元换成神经网络后,网络中神经元之间的耦合可以促进神经元的发放,耦合中的时间延迟可以增强这种促进作用,但是不会改变神经耦合对神经元发放的促进模式.

1 引 言

处理和传递信息的神经系统由大量的神经元个体构成,神经信号是编码在神经元的动作电位之中的[1,2].近年来,人们研究了不同模式的神经放电现象,Pankratova等[3]研究了Hodgkin-Huxley神经元在不同正弦电流信号刺激下的动作电位的出现情况和频率变化,Levin和Miller[4]研究了阈下频率电流刺激对神经元的动作电位的影响.与其他生物系统一样[5−9],神经系统中也存在不同的噪声和延迟[10−14],它们在很大程度上影响了神经元的放电现象.随机电流刺激对神经元动作电位的影响受到了广泛的关注[15,16],文献[17—22]指出神经元的周期发放可以弱化一些随机噪声的影响,Tang等[23]提出延迟可以促进神经网络的同步发放,我们以前的工作表明[24]异质延迟能够在很大程度上破坏神经元发放的同步性.

在神经系统中,神经信息是通过突触在神经元之间传递的[25].在神经信息的传递中,突触具有很强的变异性[26],化学浓度的变化与空间异质性都能导致突触的电导在短时间内波动,形成动态突触.在大脑中,突触传递神经信息的过程中会出现短时抑制(short-term depression,STD)机制[27],即如果一个突触前神经元的动作电位达到高频,那么伴随动作电位的神经递质释放将减少,从而使得突触后神经元的反应受到抑制.这种机制影响了大脑许多功能[28]的实现,例如皮质的增益控制[29]、神经网络的信息存储[30]、同步和选择性注意[31,32].

Uzuntarla等[33]建立了一个受阈值下周期电流和动态突触电流共同刺激的HH神经元模型,并且研究了动态突触对HH神经元首次发放潜伏期的影响.在此模型的基础之上,我们建立了只受动态突触电流激发的HH神经元发放模型,并将突触后神经元扩展成一个包含100个神经元的神经网络,网络中的神经元均受到相同的动态突触刺激,还受到神经网络内部突触的耦合刺激[34−38].本文以此模型为基础探讨了动态突触、神经网络中的突触耦合与时间延迟对HH神经元发放的影响.

2 模 型

2.1 神经元发放模型

图1(a)描述了神经元发放模型,模型中含有多个兴奋性或抑制性的突触前神经元和一个突触后神经元,所有突触前神经元通过一个总和的动态突触作用于突触后神经元.在模型中,突触后神经膜电位的时间演化遵从HH神经元模型[39],突触后神经的动力学方程为

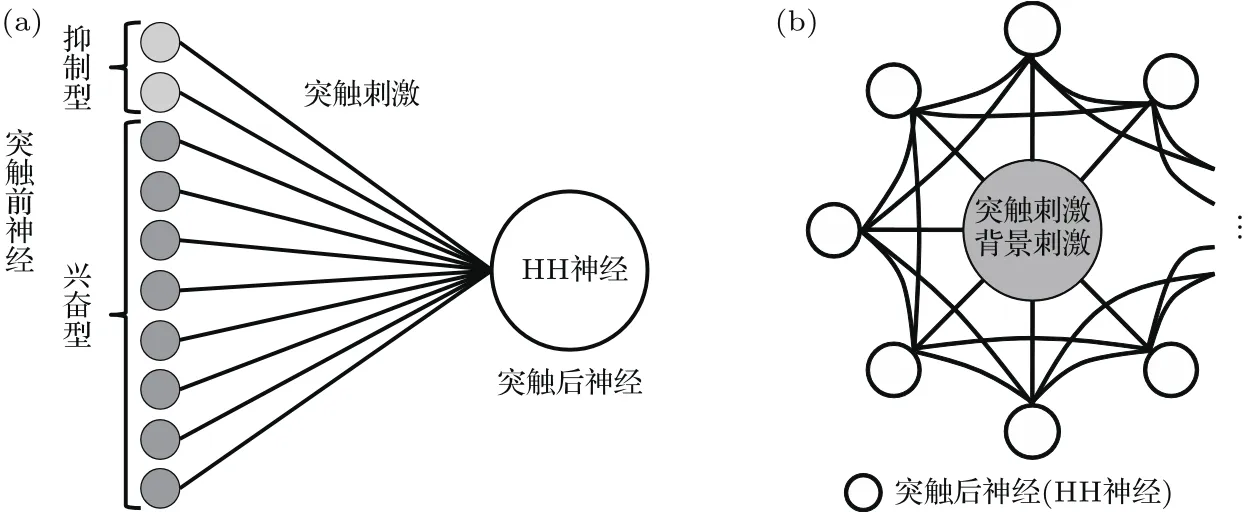
图1 模型示意图 (a)受动态突触刺激的神经元模型;(b)受动态突触刺激和背景刺激的神经网络模型Fig.1.Schematic illustration of the neuronal model:(a)A single HH neuron model subject to an activity arriving through dynamic synapses;(b)a HH neuron network model subject to both a activity arriving through dynamic synapses and background activity.

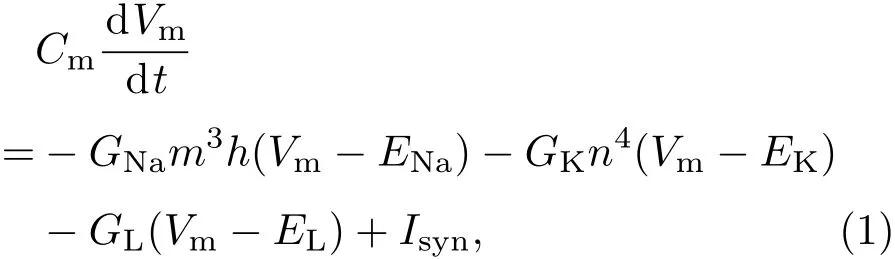
其中突触后神经元的膜电位表示为Vm,单位面积的膜电容表示为Cm=1µF/cm2;钠、钾和渗漏通道的最高电导分别为GNa=120 mS/cm2,GK=36 mS/cm2,GL=0.3 mS/cm2,三者的逆转电位分别为ENa=115 mV,EK=−12 mV,EL=10.6 mV.钠离子通道的激活和失活与钾离子通道的激活控制变量分别为m,h和n,它们遵从方程:

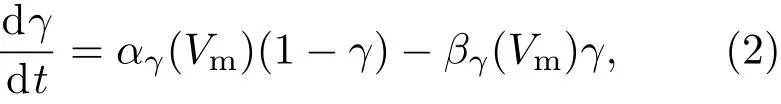
其中αγ和βγ(γ=m,n,h)为变量m,h和n的压敏率函数.文献[3]中给出了αγ和βγ的具体形式,其形式由实验数据拟合得到.

模型中神经的动态突触采取Tsodyks等[37]中提出的动态突触模型.最近的实验研究表明[40],抑制性突触与兴奋性突触一样,都能表现短时突触的可塑性,因此动态突触模型也可以用于抑制性突触[41,42].在动态突触模型中,动作电位是通过神经递质来传递的,即每个突触前神经元的动作电位以特定的释放概率(ui(t))去激活一部分神经递质,这种激活会以指数形式失活[37,43],经过恢复期τrec神经递质和突触都回到初态.这个过程表示为[37]

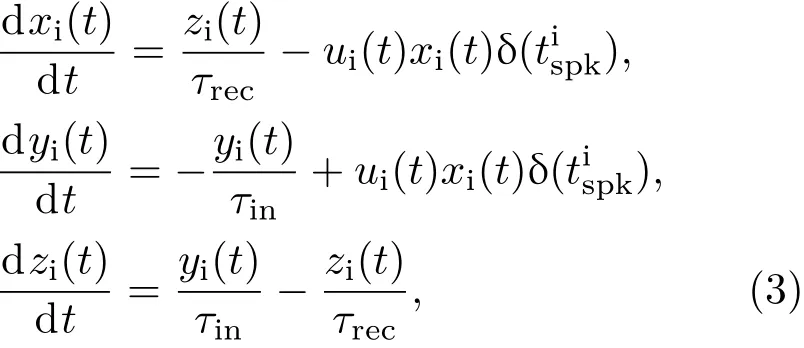
其中xi,yi,zi分别为神经递质处于恢复、活跃和失活状态的比例,神经递质失活的特征时间常数τin=3 ms,突触的恢复期τrec=100 ms.系统中每一个突触前神经元的动作电位都表现为一个频率f的泊松随机发放序列,这些动作电位出现时δ函数项计入方程.对于相互独立的突触前神经元,它们的发放率可以相等也可以不等,本文考虑了各个突触前神经元的发放率相等和服从高斯分布两种情况,以f表示相同的突触前神经元发放率,与CV表示突触前神经元发放率服从高斯分布时的平均值及变异系数.另外,在大脑皮层神经元的STD机制[37,43]下,动作电位释放神经递质的概率为常数,即ui(t)=U,本文中令U=0.67[43].

方程(1)中的Isyn为突触电流,由1000个相互独立的突触前神经元共同产生,具体形式可以表现为

其中,Ne为兴奋性突触前神经元数量,Ni为抑制性突触前神经元数量,Ne:Ni=4:1,这与哺乳动物大脑皮质中兴奋性神经和抑制性神经的比例相当[27].K为抑制性神经连接和兴奋性神经连接的相对强度,A为兴奋性连接的最大突触电流,本文中K=4,A=250 pA[43].

2.2 神经网络发放模型

为了讨论神经耦合对突触后神经元发放的影响,将单个突触后神经元换成包含100个单体的规则神经网络,该神经网络模型如图1(b)所示.图中的100个突触后神经元均受到来自于1000个突触前神经元的动态突触刺激,此神经网络中神经元的动力学方程为

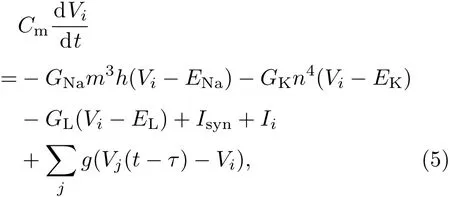
其中i为网络中神经元的编号,Vi为第i个神经元的膜电位;Isyn项为来自于1000个突触前神经元的动态突触电流,此项与2.1节中所介绍的相同,每个突触后神经元受到动态突触电流刺激均相同;Ii项是HH神经元的一个分岔参数,在其小于6时,HH神经元保持在静息状态,不会出现周期性发放,为了保证突触后神经元之间具有不同的发放特性,并且使突触后神经元在没受到任何突触刺激时保持静息状态,设Ii服从0—6之间的平均分布,且不随时间改变;方程右侧的最后一项表示神经网络中突触后神经元之间的突触耦合项,g为神经间的耦合强度,τ为突触后神经元之间信息传输的延迟时间.本文中所有的数值积分采用四阶龙格-库塔法,时间步长为10µs.

3 结果与讨论

3.1 动态突触对突触后神经元发放的影响

文献[3]研究表明,对HH神经元输入不同的电流,HH神经元会实现不同的发放状态.本节首先应用2.1节中的模型来讨论随机突触电流刺激对突触后神经元(HH神经元)发放的影响效果.

图2(a)中显示了在突触前神经元发放率f=10 Hz时,突触后神经元在一段时间内的发放情况.图中的黑线表示突触后神经元膜电位的变化,红线表示动态突触电流的变化.由图可见,伴随着随机突触电流的输入,突触后神经元的发放也表现出了随机性,其发放没有明显的周期性.统计不同f下突触后神经元在2000 ms内的发放次数,如图2(b)所示.为了消除系统中随机性对突触后神经元发放所带来的影响,图2(b)中的结果为100次计算的系综平均.如图2(b)中所示,突触后神经元发放次数的最高峰出现在f=50 Hz处,f在30—100 Hz之间时,突触后神经元发放次数较多.

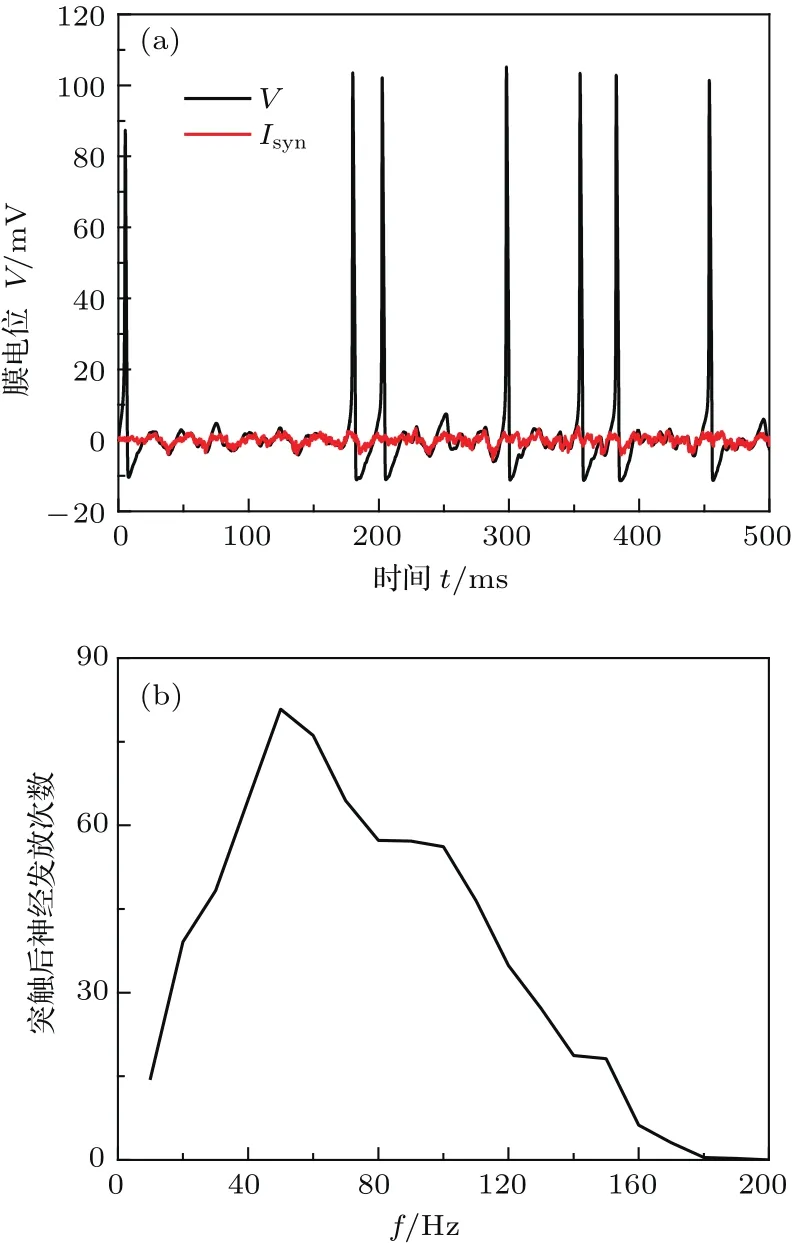
图2 (网刊彩色)突触后神经元发放 (a)突触后神经元随时间的发放(f=10 Hz);(b)突触后神经元2000 ms内发放次数随f的变化Fig.2. (color online)Firing of postsynaptic neuron:(a)Firing of the postsynaptic neurons over time(f=10 Hz);(b) firing number of postsynaptic neurons in 2000 ms for different f.

为了更清楚地分析突触电流中的频率成分,对带有随机成分的动态突触电流的时间序列做傅里叶分析.图3(a)—(c)分别为f=30,50与100 Hz时,系统动态突触电流的傅里叶分析结果,由图可见突触电流的频率成分主要集中在相应突触前神经元发放率的整数倍上,且在突触前神经元发放率的一倍或两倍时出现电流强度最大的频率,这些最大的电流强度大部分都在1.6—2.0之间.文献[3]中介绍了HH神经元在受到不同振幅和频率的正弦电流刺激下的周期发放情况,发现电流强度较小时,频率在50 Hz周围的电流会使HH神经元呈现一定频率的周期性发放.电流强度在1.6—2.0之间时,能使HH神经元呈现一定频率的周期性发放的电流输入频率范围在30—90 Hz.这说明在突触前神经元的发放率在30—90 Hz之间时,动态突触电流中电流强度最大的单频电流成分已经在一定程度上使得突触后神经元进行持续的振荡,所以此条件下的突触后神经元发放次数较多.进而将正弦电流输入HH神经元发放频率与单倍和二倍突触前神经元发放率进行了对比,如图3(d).图中所示的是频率在30—90 Hz之间的对比结果,过高频或过低频的正弦电流输入都不能使HH神经元发放.图中,正弦电流输入HH神经元发放频率基本可以与单倍或二倍突触前神经元发放率重合.同时,图中频率范围与图2(b)中显示的突触后神经元发放次数较多的突触前神经元发放率范围相符合.由此可以得到结论:突触后神经元发放次数较多,是由于输入的突触电流中一些频率的电流刺激本身就可以使得突触后神经元持续发放,这些发放不会因其他频率刺激电流的出现而被抑制.因而,动态突触电流刺激下,突触后神经元多次发放是由突触前神经元发放频率与HH神经元的固有频率发生共振所产生的.

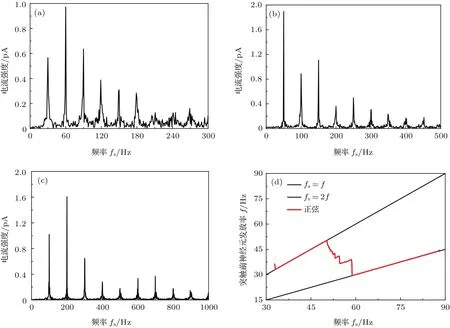
图3 (网刊彩色)动态突触电流的傅里叶变换分析 (a)f=30 Hz,(b)50 Hz和(c)100 Hz时,动态突触电流的傅里叶分解;(d)突触前神经元发放率与HH神经元发放频率的对比Fig.3.(color online)Flourier transform analysis of synaptic currents: flourier transform analysis of dynamic synaptic currents with f=30 Hz(a),50 Hz(b),100 Hz(c);(d)comparation between presynaptic neuron firing rate and HH neurons firing frequency.

进一步讨论突触前神经元发放率的异质性对突触后神经元发放的影响.这里用2.1节中介绍的模型,让突触前神经元发放率服从高斯分布,CV体现了突触前神经元发放率异质性的大小.图4(a)中显示了=50,200 Hz时突触后神经元发放次数随CV的变化情况.发现=50 Hz时发放次数随CV的增加明显减少;=200 Hz时发放次数随CV的增加而增加.图4(b)中显示了在10—200 Hz间突触后神经元发放次数的变化情况,可见在峰值频率周围的神经元的发放次数随着CV的增加有所减小;较大(大于150 Hz)的神经元发放次数随着CV的增加有所增加,这个趋势与图4(a)中表现出来的现象相同.这表明突触前神经元发放率的异质性抑制了峰值频率周围的神经元的发放,促进了突触前神经元发放率值较大的神经元发放.为了解释这一现象,仍以为50和200 Hz为例,将不同CV条件下系统的动态突触电流进行了傅里叶变换分析,如图4(c)和图4(d).图中动态突触电流的频率成分依然主要集中在相应的整数倍上,但随着CV的增加其他频率成分出现的幅度逐渐增大.两幅图中的插图的频率范围为30—90 Hz,正是文献[3]中给出的易使HH神经元进行周期性发放的频率范围.如插图中所示,=50 Hz时随着CV的增加,傅里叶分解出的电流强度有所减小,最终小于1.6,即可以以单个频率电流输入诱导突触后神经元发放的电流强度范围,根据图3中得到的结论,突触后神经元发放的次数应有所减少,这与图4(a)和图4(b)中的现象相同;=200 Hz时,傅里叶分解出的电流强度有所增加,特别是CV增加到1时,各个频率对应的电流强度增加的非常明显,图4(a)和图4(b)中显示此时突触后神经元发放的次数有所增多,这说明虽然没有任何频率的电流输入可以独立诱导突触后神经元的周期发放,但是该频率范围内的电流强度增加还是能够促进突触后神经元的发放.这说明突触电流中电流强度随频率的分布与突触后神经元发放的次数有着直接的关系.对于频率范围在30—90 Hz的突触电流,其电流强度的变化在很大程度上影响着突触后神经元的发放.突触前神经元发放率的异质性就是通过改变这些频率电流的振幅来影响突触后神经元的发放次数.

综上所述,对动态突触刺激下的突触后神经元,突触前神经元发放频率与HH神经元的固有频率发生共振使其多次发放,动态突触电流中包含频率在30—90 Hz之间的电流振幅在很大程度上决定了突触后神经元的发放情况.

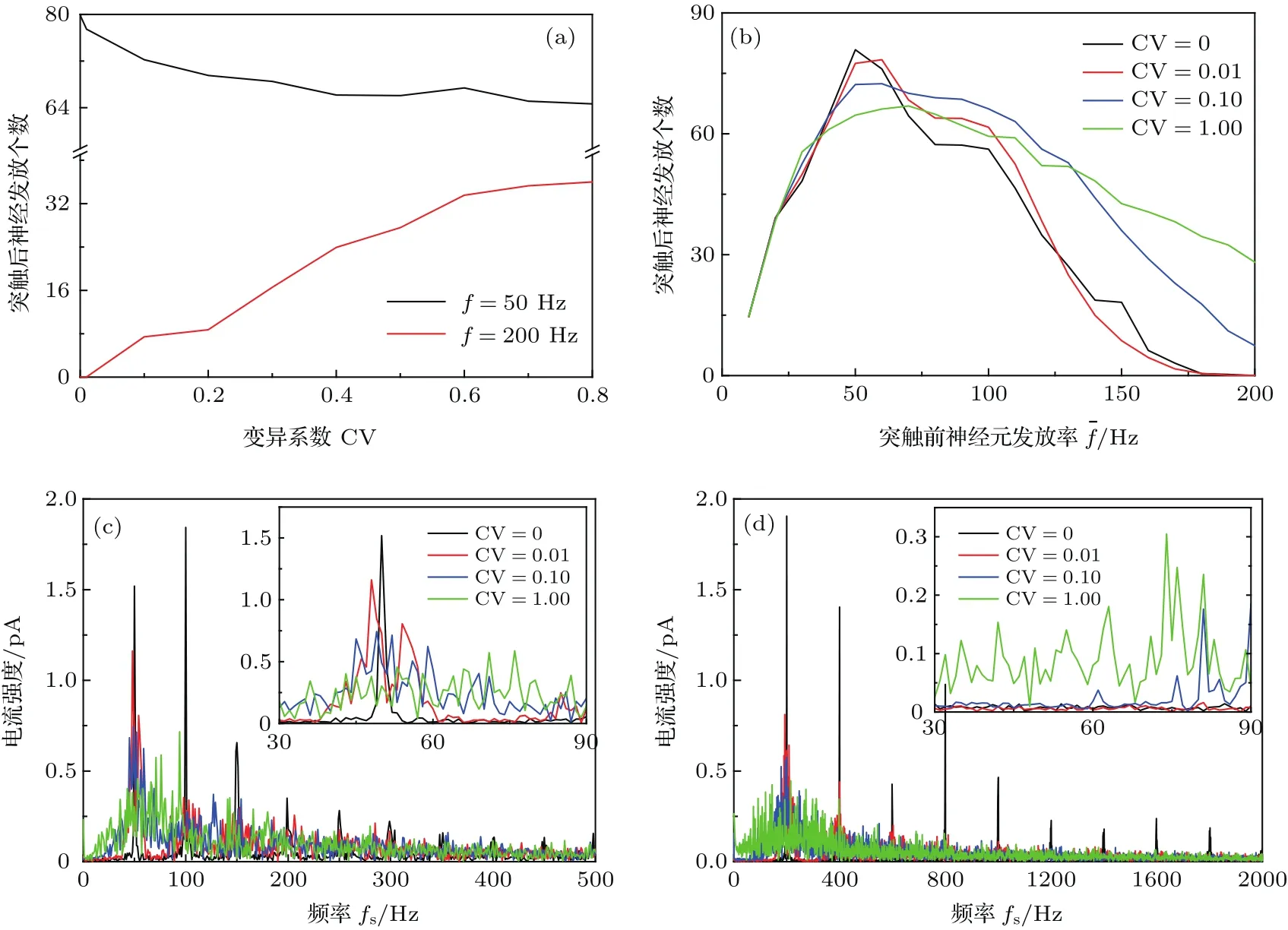
图4 (网刊彩色)高斯突触前神经元发放率下的神经元发放(a)不同¯f下,突触后神经元2000 ms内发放次数CV的变化;(b)不同CV下,突触后神经元2000 ms内发放次数随¯f的变化;(c)¯f=50 Hz与(d)200 Hz时,动态突触电流的傅里叶分解Fig.4.(color online)The firing of postsynaptic neuron under Gaussian firing rate:(a)Firing number of postsynaptic neurons in 2000 ms for different CV under different¯f;(b) firing number of postsynaptic neurons in 2000 ms for different firing rate¯f under different CV; flourier transform analysis of synaptic currents with¯f=50 Hz(c)and 200 Hz(d).

3.2 神经突触耦合与时间延迟对突触后神经元发放的影响

在2.2节中,我们将突触后神经元置换成包含100个神经元的耦合神经网络,基于该模拟,下面讨论神经网络中的突触耦合与时间延迟对突触后神经网络发放的影响.这里,主要探究耦合强度g与延迟量τ对不同突触前神经元发放率刺激下的突触后神经元发放次数的影响.此处计算神经网络每个神经元在2000 ms内的发放次数,因此发放次数实际体现了神经元的发放频率.为了减小随机性对神经元发放次数的影响,对每一个神经元的发放次数取100次系综平均,并将网络中的100个突触后神经元的发放次数取均值,得到突触后神经元平均发放次数.

首先探讨神经突触耦合对突触后神经元发放的影响,此时系统无延迟.图5(a)和图5(b)分别为f=10,200 Hz的随机电流刺激下神经网络的发放模式图,其中上侧的两幅g=0,也就是突触后神经元之间没有突触耦合;下侧的两幅g=0.08,网络之中的突触后神经元存在一定的突触耦合.从图中明显可见,下侧的两幅图中突触后神经元发放的次数比上侧的两幅图多,这可能意味着在f=10,200 Hz时的随机电流刺激下,神经的突触耦合会在一定程度上促进突触后神经元发放.突触后神经元的平均发放次数随突触前神经元发放率的变化如图5(c),这里发放率取10—200 Hz之间,基本包含了所有突触后神经元出现发放的突触前神经元发放率.图中红线和蓝线(g=0.08,0.20)都在黑线(g=0)上方,且红线(g=0.08)基本上是在蓝线(g=0.20)上方,这表明神经网络中的突触耦合会在一定程度上促进突触后神经元的发放,并且g=0.08是一个促进效果比较好的耦合强度.图5(d)给出了突触后神经元平均发放次数随耦合强度的变化情况.图中显示,g小于0.08时,突触后神经元平均发放次数随耦合强度的增加而明显增加;g大于0.08后,突触后神经元平均发放次数略有波动,但始终保持在一个比较大的数目上.综上所述,神经网络系统中的突触耦合对系统中突触后神经元的发放具有促进作用.

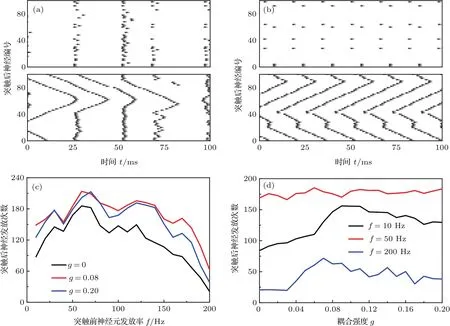
图5 (网刊彩色)神经网络中的神经元发放 耦合强度g=0(a),(b);0.08(c),(d);f=10 Hz(a),200 Hz(b);(c)突触后神经元平均发放次数随f的变化;(d)突触后神经元平均发放次数随耦合强度的变化Fig.5.(color online)The firing pattern in neuron network with coupling strength g=0(a),(b);0.08(c),(d);f=10 Hz(a)and 200 Hz(b);(c) firing number of postsynaptic neurons for different f;(d) firing number of postsynaptic neurons for different coupling strength.

进一步讨论时间延迟对突触后神经元发放的影响,此时取神经耦合强度为0.08,突触后神经元在此耦合强度下发放的次数较多.图6(a)以延迟量τ为10 ms、突触前神经元发放率f为10,200 Hz时的神经发放模式图,对比图5(a)和图5(b)下侧的两幅图可以清楚地发现,τ为10 ms时突触后神经元的发放次数比无延迟时的发放次数多,这似乎说明延迟可以促进突触后神经元的发放.为了进一步说明这一现象,统计了τ在1—1000 ms之间时,突触后神经元的发放次数,如图6(b)所示.图中的三条线(f=10,50,200 Hz)上的点均大于延迟较小时突触后神经元发放次数,这说明在比较广泛的延迟范围内,延迟对突触后神经元发放具有促进作用.并且,图中三条线的峰都在τ=10 ms处出现,说明此处延迟对突触后神经元发放的促进作用最强.对比τ为0 ms和10 ms时突触后神经元发放个数随耦合强度g的变化,图6(c)和图6(d)分别为f=10与200 Hz的情况,可见两幅图中的四条线的变化模式相同,均经历了g小于0.03时发放次数较少、g在0.03—0.08之间的发放次数快速增长和g大于0.08时发放次数保持在较高的值.这说明时间延迟促进了突触后神经元的发放,却不改变耦合强度对突触后神经元发放的促进模式.

图6 (网刊彩色)延迟神经网络中的发放 (a)τ=10 s时,突触后神经发放图[f=10 Hz(上),f=200 Hz(下)];(b)突触后神经平均发放次数随延迟量τ的变化;(c)f=10 Hz,(d)200 Hz时,突触后神经平均发放次数随耦合强度的变化Fig.6.(color online)The firing in delayed neuron network:(a)Firingpattern of postsynaptic neuronswith τ=10 s[f=10 Hz(top),f=200 Hz(bottom)];(b) firing number of postsynaptic neurons for different delay τ;(c)f=10 Hz and(d)200 Hz firing number of postsynaptic neurons for different firing rate.

综上所述,在具有动态突触的神经网络发放模型中,神经突触耦合可以促进突触后神经元的发放,突触耦合中的时间延迟可以加强这种促进效果,但是不会改变神经突触耦合对突触后神经元发放的促进模式.

4 结 论

基于一个动态突触电流刺激下的神经模型,研究了影响突触后神经元(HH神经元)发放的因素.通过傅里叶变换分析法和系综平均法,分别分析了随机突触电流的频率——振幅分布和随机系统中突触后神经元的发放次数的变化.研究表明:突触前神经元发放频率与HH神经元的固有频率发生共振决定了突触后神经元的发放率,动态突触电流中频率为30—90 Hz的电流强度在很大程度上影响了突触后神经元的发放频率;神经之间的突触耦合可以促进突触后神经元的发放,突触耦合中的时间延迟可以强化这种促进作用,但是不会改变神经突触耦合对突触后神经元发放的促进模式.

[1]Hartmann G,Hauske G,Eckmiller R 1990Parallel Processing in Neural Systems and Computers(Amsterdam:Computing and Computers)

[2]Vanrullen R,Guyonneau R,Thorpe S J 2005Trends Neurosci.28 1

[3]Pankratova E V,Polovinkin A V,Mosekilde E 2005Eur.Phys.J.B45 391

[4]Levin J E,Miller J P 1996Nature380 165

[5]Tang J,Liu T B,Ma J,Luo J M,Yang X Q 2016Commun.Nonlinear Sci.Numer.Simulat.32 262

[6]Duan W L,Zeng C 2017Appl.Math.Comput.292 400

[7]Yu W T,Tang J,Luo J M 2015Acta Phys.Sin.64 068702(in Chinese)[于文婷,唐军,罗进明2015物理学报64 068702]

[8]Yu W T,Tang J,Ma J,Luo J M,Yang X Q 2015Eur.Biophys.J.44 677

[9]Zeng J,Zeng C,Xie Q,Guan L,Dong X,Yang F 2016Physica A462 1273

[10]Johnson J B 1928Phys.Rev.32 97

[11]Gu H,Zhao Z 2015Plos One10 e0138593

[12]Qian Y 2014Plos One9 e96415

[13]Guo D,Wang Q,Perc M 2012Phys.Rev.E85 878

[14]Liu S,Wang Q,Fan D 2016Front.Comput.Neurosc.10 81

[15]Mainen Z F,Sejnowski T J 1995Science268 1503

[16]Jun M A,Tang J 2015Sci.China:Technol.Sc.58 2038

[17]Chialvo D R,Longtin A,Müautllergerking J 1997Phys.Rev.E55 1798

[18]Gammaitoni L,Hänggi P,Jung P,Marchesoni F 1998Rev.Mod.Phys.70 254

[19]Guo D,Li C 2012J.Theor.Biol.308 105

[20]Xiao W W,Gu H G,Liu M R 2016Sci.China:Technol.Sci.59 1

[21]Liu F,Yu Y,Wang W 2001Phys.Rev.E63 051912

[22]Sakumura Y,Aihara K 2002Neural Proc.Lett.16 235

[23]Tang J,Ma J,Yi M,Xia H,Yang X Q 2011Phys.Rev.E83 046207

[24]Yu W T,Tang J,Ma J,Yang X Q 2016Europhys.Lett.114 50006

[25]Song X L,Wang C N,Ma J,Tang J 2015Sci.China:Technol.Sci.58 1

[26]Markram H,Wang Y,Tsodyks M 1998Proc.Natl.Acad.Sci.USA95 5323

[27]Braitenberg V,Schüz A 1991Anatomy of the Cortex:Statistics and Geometry(Berlin:Springer-Verlag)

[28]Torres J J,Kappen J H 2013Front.Comput.Neurosci.7 30

[29]Abbott L F,Varela J A,Sen K,Nelson S B 1997Science275 221

[30]Torres J J,Pantic L,Kappen H J 2002Phys.Rev.E66 061910

[31]Mishra J,Fellous J M,Sejnowski T J 2006Neural Networks19 1329

[32]Fan D,Wang Z,Wang Q 2015Commun.Nonlinear Sci.Numer.Simulat.36 219

[33]Uzuntarla M,Ozer M,Ileri U,Calim A,Torres J J 2015Phys.Rev.E92 062710

[34]Qian Y,Zhao Y,Liu F,Huang X,Zhang Z,Mi Y 2013Commun.Nonlinear.Sci.18 3509

[35]Qian Y,Liao X,Huang X,Mi Y,Zhang L,Hu G 2010Phys.Rev.E82 026107

[36]Hodgkin A L,Huxley A F 1952J.Physiol.117 500

[37]Tsodyks M V,Pawelzik K,Markram H 1998Neural Comput.10 821

[38]Fitzpatrick J S,Akopian G,Walsh J P 2001J.Neurophysiol.85 2088

[39]Tecuapetla F,Carrillo-Reid L,Bargas J,Galarraga E 2007Proc.Natl.Acad.Sci.USA104 10258

[40]Ma Y,Hu H,Agmon A 2012J.Neurosci.32 983

[41]Barroso-Flores J,Herrera-Valdez M A,Lopez-Huerta V G,Galarraga E 2015J.Bargas Neural Plast.2015 573543

[42]Tsodyks M,Uziel A,Markram H 2000J.Neurosci.20 RC50

[43]Tsodyks M V,Markram H 1997Proc.Natl.Acad.Sci.USA94 719

E ff ects of dynamic synapses,neuronal coupling,and time delay on firing of neuron∗

Yu Wen-Ting Zhang Juan Tang Jun†

(School of Physics,China University of Mining and Technology,Xuzhou 221116,China)

15 May 2017;revised manuscript

29 June 2017)

Neuronal firing plays a key role in the neuronal information transmission,and different neuronal firing patterns are reported,such as spiking,bursting.A number of neuron models are introduced to reproduce the firing patterns of single neuron or neuronal network.The key factors determining the firing pattern gain more and more attention in the study of neuron system,such as noise,network topology.Noise is able to induce sub-or super-threshold coherent neuronal firing easily,and a number of coherence resonances are reported in the noise induced firing.The network topology determines the synchronization of the firing patterns of the neuronal network,and the change of network topology may induce fruitful synchronization transitions.It is well known that synapses exhibit a high variability with a diverse origin during information transmission,such as the stochastic release of neurotransmitters,variations in chemical concentration through synapses,and spatial heterogeneity of synaptic response over dendrite tree.The collective e ff ect of all of these factors might result in the notion of dynamic synapses.In reality,the neuronal network often involves time delay due to the?nite signal propagation time in biological networks.Recently,neuronal networks with time delay have received considerable attention.Delay-sustained neuronal firing patterns may be relevant to neuronal networks for establishing a concept of collective information processing in the presence of delayed information transmission.According to the above-mentioned motivations,the firing dynamics of the single postsynapic neuron is investigated based on a simple postsynaptic neuron model by using numerical simulation and Fourier transform analysis.In this model,the postsynapic neuron receives dynamic synaptic currents from a population of presynaptic neurons.It is found that the firing rate resonance between the pre-and postsynaptic neuron determines the firing of the postsynaptic neuron.Stimulus currents in speci fi c frequency range are easy to stimulate postsynaptic neuron firing.The random currents released from dynamic synapses determine the postsynaptic firing rate.Then the single postsynaptic neuron is extended to a neuronal network,in which 100 neurons connect to its 4 nearest neighbors regularly and receive delayed synaptic currents from connected neurons.All the neurons in the network receive the same dynamic synaptic currents from the presynaptic neurons.The results show that the synaptic coupling in the network is able to promote the neuron firing in the network,and time delay in the synaptic coupling could reinforce the promotion,but the mode of the promotion is not changed.

neuron,synaptic stimulation,Flourier transform,time delay

(2017年5月15日收到;2017年6月29日收到修改稿)

10.7498/aps.66.200201

∗中央高校基本科研业务费(批准号:2015XKMS080(TJ))资助的课题.

†通信作者.E-mail:tjuns1979@126.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:02.30.Nw,05.45.–a,05.40.–aDOI:10.7498/aps.66.200201

*Project supported by the Fundamental Research Funds for the Central Universities,China(Grant No.2015XKMS080(TJ)).

†Corresponding author.E-mail:tjuns1979@126.com