一种基于金刚石多层波导结构微环谐振器的仿真分析∗
2017-11-12李志全白兰迪顾而丹谢锐杰刘同磊牛力勇冯丹丹岳中
李志全 白兰迪 顾而丹 谢锐杰 刘同磊 牛力勇 冯丹丹 岳中
(燕山大学电气工程学院,秦皇岛 066004)
一种基于金刚石多层波导结构微环谐振器的仿真分析∗
李志全 白兰迪†顾而丹 谢锐杰 刘同磊 牛力勇 冯丹丹 岳中
(燕山大学电气工程学院,秦皇岛 066004)
金刚石芯层,微环谐振器,多层脊型波导结构
提出了一种以金刚石新型材料为芯层的单微环谐振器模型.谐振器的纵切面采用五层脊形波导结构,中间一层设定为金刚石,上下两侧分别是SiO2和As2S3,即As2S3-SiO2-金刚石-SiO2-As2S3.设置操作波长为1550 nm,依据耦合膜理论和微环谐振理论,利用Comsol软件仿真模拟了单直波导纵切面、直波导和环形波导耦合区的纵切面以及微环在谐振波长为1543 nm时的场强分布,及直波导和环形波导耦合区间距改变时微环的场强分布和传输特性.在此基础上,依据传输矩阵法讨论了微环的品质因数、耦合系数变化对输出光谱的影响,并对微环损耗进行了讨论.结果表明:以金刚石为芯层的微环谐振器具有良好的光学特性,本结构在谐振波长为1543 nm时谐振峰值达到了−12 dB以上,品质因数达到了1.54×105,在耦合系数为0.01时,自由光谱范围约为40 nm.
1 引 言
自20世纪90年代,Chin和Ho[1]提出了双信道单微环的谐振滤波器的设计以来,人们开始了对微环谐振器应用于滤波的研究.随着研究的深入,这种新颖的设计很快渗透到了各种传感器、波分复用器和高速调制器等方面,并且在新一代全光通信系统和集成光学器件的设计制作中展现出了极具潜力的应用前景[2−4].
微环谐振器具有滤波性能稳定、结构紧凑、可集成度高等优点,并且具备极大的自由光谱范围(free spectral range,FSR)、窄带宽和高消光比等独特优势,能够有效地提高传感器的量程、灵敏度和分辨力等指标,是作为滤波器、微环传感器或微环光开关的理想核心器件[5].现行的设计方式往往通过诸如缩小微环半径和并联多个微环等方法来提高这些指标,但这些方法也增加了制作工艺的复杂度、易增加传输损耗[6].因此,本设计通过引入具备较高折射率的金刚石作为芯层材料,以提升谐振器的品质因数.
金刚石合成技术的提升以及其在波导方面的研究进展,使得光子学研究人员开始探索金刚石的光学特性,以便应用于各光学领域.近年来利用金刚石制作波导结构已经取得了显著的进展,为制作金刚石基光子芯片提供了良好的基础和契机[7−12].目前金刚石波导已经被成功应用于量子光学,并表现出独特优越特性[10−12].文献[13]中提出了一种基于金刚石-二氧化硅的环形谐振器,用于转换波长激光器的设计,揭示并验证了利用金刚石制作环形谐振器的可行性.现行的微环波导结构有金属-绝缘体-金属(metal-insulator-metal,MIM)型,这种结构虽然具有良好的电场限制,但大多数结构存在传播距离较短,品质因数较低的缺点.近年来,硅基光子学得到了很大的发展,由于其能够与互补金属氧化物半导体(CMOS)工艺相兼容,因此广泛应用于光学波导的制作,并具有规模化生产的潜在优势[14,15],但硅材料最主要的缺憾是,在波长低于2.2µm时,会受到强烈的非线性双光子吸收(twophoton absorption,TPA)和TPA-感应自由载流子吸收(free carrier absorption,FCA)[13],从而产生较大的非线性损耗,而金刚石恰恰可以弥补这一缺点,且也可以与CMOS工艺相兼容,具有可集成性.
本文提出的微环谐振器采用传统的单环双直波导结构,设计了以SiO2为基底的As2S3-SiO2-金刚石-SiO2-As2S3脊型五层波导结构,利用Comsol软件研究了谐振波长为1543 nm时的微环纵切面的场强分布,也给出了双直波导在散射边界条件下谐振时的场强分布,并分析了直波导与微环间距对谐振波长以及谐振峰的影响.利用Matlab软件对结构的品质因数、耦合系数和自由光谱范围进行了仿真与计算.
2 金刚石微环谐振器的理论分析
图1给出了双直波导微环谐振器的结构图.图1(a)为结构的三维图,其中基底为SiO2,直波导与微环波导均采用同一种混合材料,在图2中对其切面进行了详细分析.图1(b)为结构的俯视图,该结构的工作原理是光信号从端口1输入,在耦合区I通过信道波导与微环之间的耦合进入微环,随后微环中的光信号在耦合区II进入下信道,从端口3输出.当入射光波长λ满足谐振条件2πRneff=pλ时,微环发生谐振,传输效率达到最大值(neff为有效折射率,R为微环半径,p为谐振级次),依据耦合模理论,采用传输矩阵法建立本结构的数学模型.设微环周长L=2πR,E1为端口1的输入场强,E2为上信道直波导端口2的输出场强,E3为经两耦合区耦合后端口3的输出场强,E4为端口4可输入场强;ei(其中i=1,2,3,4)为光耦合进微环中四个部分的场强.设耦合区的自耦合因子为t,互耦合因子为ik,在无损情况下满足t2+k2=1,光在微环中的传输损耗为α,且有α=exp(−σL),其中σ为波导损耗系数.可得传输矩阵如(1)式和(2)式[16]:




图1 (网刊彩色)双直波导微环谐振器结构图 (a)立体结构图;(b)结构俯视图Fig.1.(color online)Double straight-wave micro-ring resonator structure:(a)The three-dimensional structure;(b)top view of the structure.
由于只设置端口1为光输入口,因此E4=0,则根据传输矩阵公式可以得到上下端口的输入光场与输出光场的关系式:
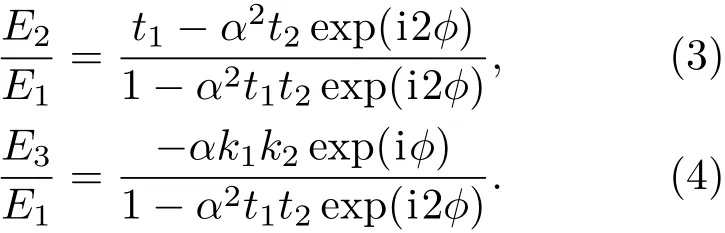
根据(3)式和(4)式,可得微环结构的上下传输端口的归一化光强:

本结构的设计思想参考了文献[17,18]中提出的多层波导结构,在传统的MIM结构上,设计了基底为SiO2,芯层为金刚石,上下采用SiO2材料的结构,并在此基础上引入As2S3缓冲层,以减少场内能量粒子的交互作用,降低光在波导中传播时的损耗.设计中,单一的脊型波导纵切面如图2(a)所示,设金刚石芯层厚度为m,上下临近的SiO2层厚度分别为b1,b2.最外层为As2S3层,厚度分别为c1,c2.脊宽设置为ω1.可将纵切面分为三个区域,一区和三区为空气层,neff1=neff3,二区有效折射率为neff2.图2(b)为直波导与微环波导耦合区的纵切面,两波导间距设为S.波导的能量转换效率受S的影响,此处是直波导与微环的耦合区,可视为一个定向耦合器.另外在设计中需保证直波导和环形波导结构的纵切面结构、材料相一致,从而使得光在波导间传播时相位匹配,以减少损耗,提高品质因子.

图2 (网刊彩色)环形谐振器纵切面波导结构图 (a)单一的脊型波导纵切面;(b)脊型直波导与微环波导耦合区的纵切面Fig.2.(color online)Structure of longitudinal section waveguide of ring resonator:(a)Vertical-section of single ridge waveguide;(b)vertical-section of the coupled rib waveguides(bus and ring).
3 金刚石微环谐振器模型仿真与结果分析
3.1 模型参数设置与仿真
设定操作波长为λ=1550 nm,根据设计结构定义参数如下:c1=450 nm,c2=400 nm,b1=b2=40 nm,m=20 nm,w1=500 nm,R=1800 nm(依据谐振条件求得).通过调整As2S3的厚度,使得电场获得了良好的局域分布特性.独立的脊型波导结构仿真波长范围控制在1300—1700 nm,用以确保ne ff的独立性.采用Comsol软件对结构进行仿真,一和三区的有效折射率neff=1.0,芯层折射率为2.42,利用文献[19]提出的Sellmeier公式可得出SiO2和As2S3的折射率分别为1.42,2.35.仿真结果如图3所示,为单一波导纵向切面场强分布,图中反映出电场的高能区主要分布在芯层周围,沿着芯层向上下方向迅速衰减.图4(a)和图4(b)分别为直波导与环形波导间耦合区纵切面在对称、非对称模式下的场强分布,耦合区的这两种模式影响耦合区的长度,此长度也是仿真设计中的一个重要指标.
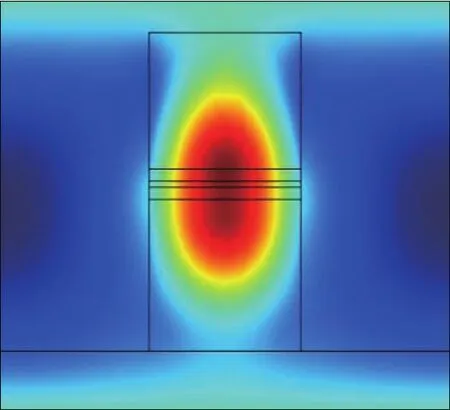
图3 (网刊彩色)单一波导纵向切面场强分布Fig.3. (color online)Field component of verticalsection of the single waveguide.

图4 (网刊彩色)直波导与环形波导间耦合区纵切面在对称、非对称模式下的场强分布 (a)对称模式;(b)非对称模式Fig.4.(color online)Field distribution of verticalsection in the symmetric and asymmetric modes of the coupling between the direct waveguide and the annular waveguide:(a)Symmetric mode;(b)asymmetric mode.
利用Matlab软件对微环谐振器进行仿真,设置波长为1300—1700 nm,得到不同波长下端口2与端口3的输出场强分布如图5所示.从响应曲线的分布可知,端口2与端口3的输出场强呈互补趋势,当入射光最大程度地耦合进微环谐振器,并经由端口3输出时,可明显看到在谐振峰处,入射波与微环谐振器满足相位匹配条件,取达到谐振条件的谐振波长1543 nm点进行仿真,结果如图6所示,可以发现微环谐振器出现明显的谐振现象,此时光通过端口1射入直波导,经耦合区I,II从端口3输出,由于环形波导小半径弯曲率的影响,导致光在微环中传播时产生一定的能量损耗,此损耗可通过增大微环半径进行补偿,或是通过改变半导体材料设置更高的电场限制.
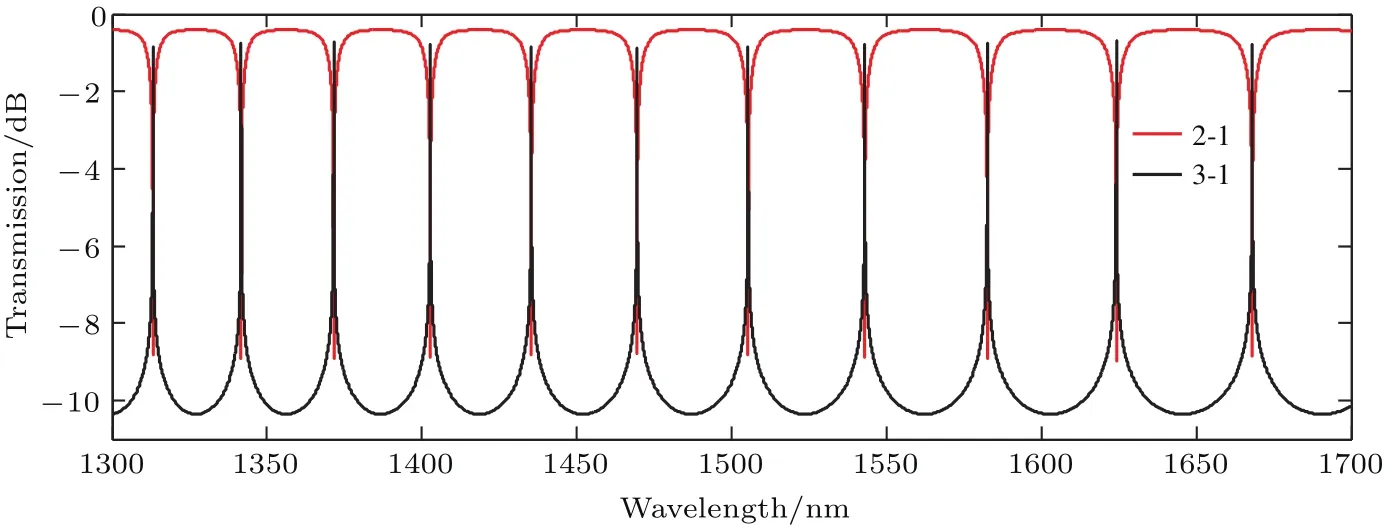
图5 (网刊彩色)双直波导上下端口随波长变化的光谱响应曲线Fig.5.(color online)Spectral response curves of the upper and lower ports of double straight waveguide.

图6 (网刊彩色)谐振波长为1543 nm时微环谐振腔的场强分布Fig.6.(color online)Field intensity distribution of the micro-ring resonator at resonant wavelength of 1543 nm.
3.2 仿真结果分析
光在谐振器的微环和上下信道中传输时的传输损耗主要包括散射损耗、泄漏损耗、弯曲损耗.结构中,为避免光的散射损耗和泄漏损耗,增设了硫化砷缓冲层,因此,影响微环谐振器输出的主要是弯曲损耗.由(1)—(4)式可绘出损耗系数σ对谐振波长输出光谱的影响.取耦合系数k1=k2=0.01,由图7可知,随着损耗因子的增大,谐振波长峰值逐渐下降.因此,减小弯曲波导损耗对于获得微环谐振器至关重要.由于波导芯层与周围介质的折射率差越大,弯曲损耗越小,而相对于传统Ag芯层,金刚石具有很高的折射率,因此作为芯层材料有利于降低损耗.
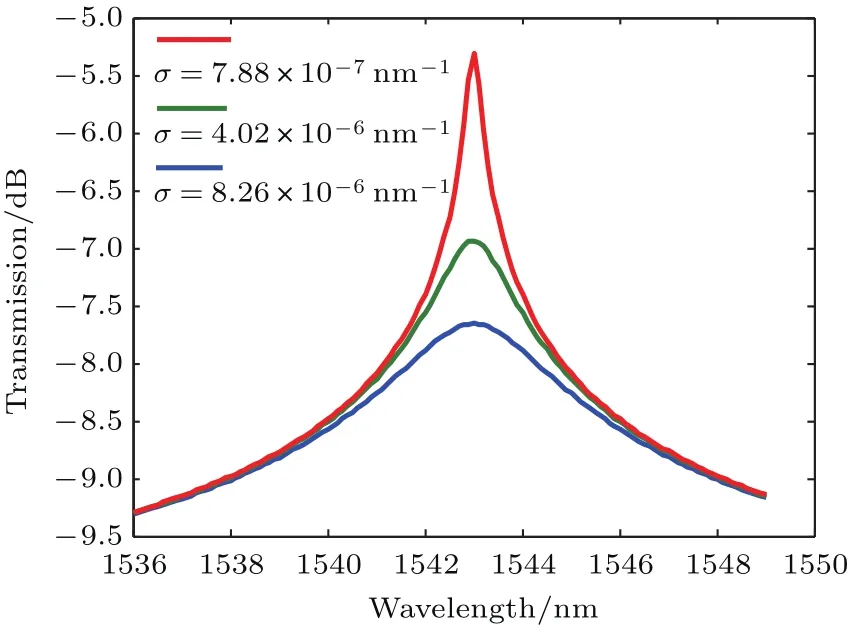
图7 微环弯曲损耗对谐振波长下输出光谱的影响Fig.7.The e ff ection of the output spectrum with the change of micro-ring bending loss.

图8 谐振波长为1543 nm时输出光谱的响应曲线Fig.8.Response curve of the output spectrum at resonant wavelength of 1543 nm.
品质因数是衡量微环谐振腔频率选择性的一个重要参数,其大小反映了输出光谱的尖锐程度.谱线锋越尖锐,则微环波长选择性越好.品质因数由谐振波长与波峰半高全宽决定,关系式为

式中Q为品质因数,λ0为谐振波长,FWHM为波峰半高全宽.图8展示了在谐振条件下光从端口3输出,谐振波长为1543 nm点附近输出光谱的响应曲线,可知在谐振点处输出场强呈现尖锐的波峰,峰值约为13.6 dB,且表现出很高的品质因数,在谐振波长为1543 nm点处,品质因数大约达到了1.54×105.
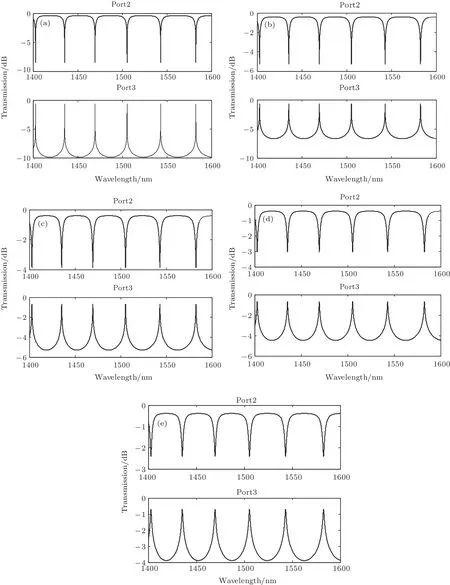
图9 耦合系数k取不同值时,端口2与输出端口3的光谱响应 (a)k=0.01;(b)k=0.05;(c)k=0.1;(d)k=0.15;(e)k=0.2Fig.9.The spectral response of port 2 and output port 3 when the coupling coefficient k takes a different value:(a)k=0.01;(b)k=0.05;(c)k=0.1;(d)k=0.15;(e)k=0.2.
另外,耦合系数k是影响微环谐振器带宽与输出强度的重要因素,当自耦合因子t越接近1,由公式t2+k2=1可知k越小,表示互耦合越弱,这意味着微环中存储的光能量越不容易耦合到上直波导中,这就保证了微环中更高的光能量通过下信道输出.图9展示了耦合系数k取不同值时,端口2与输出端口3的光谱响应曲线.由图可观察到随着k值的增大,虽然输出光谱仍具有周期性,但谐振峰强度却逐渐变弱,消光比逐渐降低,谐振波长对应的输出光强逐渐减少,且随着带宽的增大,谐振波长处的滤波效果逐渐变差,当k增加到0.1时,大多数波长的消光比减小到原来的一半.因此,k为0.01时,端口2与3的输出光谱均有较好的滤波特性,此时FSR约为40 nm,达到了较高水平,适合应用于滤波或传感器件的开发.
在实际操作当中,耦合系数k是通过调节微环与上下信道的间距S实现的,因此本文通过Comsol软件对实际制作时的间距S对所设计结构光谱响应的影响进行了仿真.图10展示了S分别为50,60,70,80 nm时的光谱响应.观察曲线可知在S为50 nm时输出场强峰值最大,随着间距S值的增加,输出场强减小,所需谐振波长也逐渐增大,这是由于参数S与直波导与环形波导的耦合能量有关,而光在耦合区的传输又对品质因数有很大影响,因此,品质因数Q与间距S有关,间距S越大,直波导与环形波导的能量交换时间越长,两者耦合越微弱,谐振峰对应的谐振频率也越大,这是由于此时的电场分布产生了很大的横向衰减.即有:对于相同结构,电场限制随着波长的增加而降低,此时会产生较大的模态直径,正是由于模态直径的增加,导致了谐振峰的偏移.

图10 不同间距S值下的光谱响应Fig.10.Spectral response at different gap S.
材料加工与处理产生的误差主要体现在制作波导时材料的尺寸上.接下来分析当S有微小变化时,输出光谱峰值的变化情况.图11绘出了在谐振波长为1568 nm点处,S在50—53 nm范围内变化时,光谱输出峰值变化情况.由拟合曲线可知,在微小变化范围内,光谱输出峰值与S尺寸变化线性相关.

图11 S变化时的输出光谱峰值曲线Fig.11.Output spectrum peak curve with the change of S.
4 结 论
金刚石的光学特性和应用研究成果表明这种特殊的材料在光学领域的应用也受到了各个研究者的关注,因其具备较高的有效折射率,光学性能良好,因此本文提出了以金刚石新型材料为芯层的微环谐振器,纵切面采用多层波导结构,分析了单环双直波导的理论基础,利用Comsol仿真软件建立了结构模型,并利用Matlab软件分析了耦合系数k为0.01时,本结构具有良好的光学效果.此外,对结构的品质因数进行了分析计算,得出此结构的品质因数达到了1.54×105,较高的品质因数不仅对波长选择性有很大的影响,而且有利于将结构应用于传感领域.本文通过仿真得出当直波导与微环波导间距S为50 nm时,谐振效果最佳,且具有很好的消光比.本结构的提出,拓展了金刚石在光学领域的应用,并为光学集成芯片的开发提供了一定的指导意义.
[1]Chin M K,Ho S T 1998J.Lightwave Technol.16 1433
[2]Hong J X,Liu Y,Chen W 2014J.Optoelectr.Laser25 1668(in Chinese)[洪建勋,刘莹,陈伟 2014光电子·激光25 1668]
[3]Dong P,Sha fi iha R,Liao S,Liang H,Feng N N,Feng D Z,Li G L,Zheng X Z,Krishnamoorthy A V,Khiavi M A 2010Opt.Express18 10941
[4]Wang W,Zhang A H,Yang K,Yang L J,Feng S J,Wang Z 2013Infrared Laser Eng.42 2162(in Chinese)[王巍,张爱华,杨铿,杨丽君,冯世娟,王振 2013红外与激光工程42 2162]
[5]Tian H,Zhang Y D,Qi D W,Su R Z,Bai Y,Xu Q 2016Chin.Phys.B25 064204
[6]Zhang X,Li Z Q,Tong K 2014Acta Phys.Sin.63 094207(in Chinese)[张鑫,李志全,童凯 2014物理学报63 094207]
[7]Lin X S,Huang X G 2008Opt.Lett.33 2874
[8]Liu J Q,Wang L,He M D,Huang W Q,Wang D Y,Zou B S,Wen S H 2008Opt.Express16 4888
[9]Tao J,Huang X G,Lin X S,Zhang Q,Jin X P 2009Opt.Express17 13989
[10]Lin X,Huang X 2009Opt.Soc.Am.B26 1263
[11]Gong Y K,Wang L R,Hu X H,Li X H,Liu X M 2009Opt.Express17 13727
[12]Tao J,Huang X G,Lin X S,Chen J H,Zhang Q,Jin X P 2010Opt.Soc.Am.B27 323
[13]Vermeulen N,Sipe J E,Helt L G,Thienpont H 2012Laser Photon.Rev.6 793
[14]Jiang X Q,Li G Y,Wei Y X,Yang J Y,Wang M H 2011National 15th Optical Fiber Communication and the 16th Annual Meeting of Integrated OpticsXi’an June 26,2011 p1
[15]Lin Q,Zhang J D,Fauchet P M,Agrawal G P 2006Opt.Express14 4786
[16]Jin L 2012Ph.D.Dissertation(Zhejiang:Zhejiang University)(in Chinese)[金磊 2012博士学位论文 (浙江:浙江大学)]
[17]Guo J P,Adato R 2008Opt.Express16 1232
[18]Li Z Q,An D Y,Zhang X,Zhao L L,Sha X P,Guo S L,Li W C 2015Spectrosc.Spect.Anal.35 2660(in Chinese)[李志全,安东阳,张鑫,赵玲玲,沙晓鹏,郭士亮,李文超2015光谱学与光谱分析35 2660]
[19]Boudebs G,Cherukulappurath S,Guignard M,Troles J,Smektala F,Sanchez F 2004Opt.Commun.230 331
Simulation analysis of micro-ring resonator based on diamond multilayer waveguide structure∗
Li Zhi-Quan Bai Lan-Di†Gu Er-Dan Xie Rui-Jie Liu Tong-LeiNiu Li-Yong Feng Dan-Dan Yue Zhong
(Institute of Electrical Engineering,Yanshan University,Qinhuangdao 066004,China)
6 May 2017;revised manuscript
31 May 2017)
With the development of the technology for fabricating high-quality synthetic diamond and diamond waveguide structures,more and more researchers are being involved in exploring the particular optical properties of diamond for different applications.Because of its high refractive index and nontoxicity to biological species,diamond can be used to make micro-ring resonator to detect the concentration of liquid or gas.In this paper,a single micro-ring resonator model with diamond serving as the core layer is proposed.In the model,the vertical-section of the waveguide adopts a fi ve-layer ridge-type waveguide structure based on As2S3,SiO2and diamond,i.e.As2S3-SiO2-Diamond-SiO2-As2S3.To investigate the optical properties of the resonator,the vertical-section of the single straight waveguide,the coupling region of the direct waveguide,and the ring waveguide are simulated with the adopted operating wavelengthλ=1550 nm based on the coupling mode theory and micro-ring resonance theory.In addition,the distribution of the fi eld strength for the micro-ring is described at a resonant wavelength of 1543 nm.It is very important to explore the fi eld intensity distribution of the micro-ring for understanding how the light transmits.The transmission characteristics of the microring with the change of the distance between the straight waveguide and the ring waveguide in the coupling region are also simulated.The quality factor and the in fl uence of the coupling coefficient change on the output spectrum are studied by the transfer matrix method and the micro-ring loss is discussed.It is shown that the micro-ring resonator designed with the diamond material has good transmission characteristics.When the resonant wavelength is 1543 nm,the resonant peak reaches more than−12 dB.The quality factor is about 1.54×105.When the coupling coefficientkis 0.01,the free spectral range is about 40 nm.The coupling coefficientkis determined by the distanceSof the coupling region.The results show that whenSis equal to 50 nm,the output spectrum has a good extinction ratio and is better compared with the other values.The error of material processing is mainly a ff ected by size,so the output spectrum near the distanceS=50 nm is studied.The result shows that in the tiny change scope,the spectral output peak is linearly related toS.The structure we suggested in this paper expands the application scope of diamond in the fi eld of optics,and provides some guiding signi fi cance for developing the optical integrated chips.
diamond core layer,micro-ring resonator,multi-layer waveguide ridge structure
(2017年5月6日收到;2017年5月31日收到修改稿)
10.7498/aps.66.204203
∗河北省自然科学基金(批准号:F2017203316)资助的课题.
†通信作者.E-mail:lzq54@ysu.edu.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
PACS:42.60.Da,43.20.Mv,81.05.ugDOI:10.7498/aps.66.204203
*Project supported by the Natural Science Foundation of Hebei Province,China(Grant No.F2017203316).
†Corresponding author.E-mail:lzq54@ysu.edu.cn
