离散发热器件基于火积耗散率最小和最高温度最小的构形优化比较∗

王刚谢志辉范旭东陈林根 孙丰瑞

1)(海军工程大学热科学与动力工程研究室,武汉 430033)

2)(海军工程大学舰船动力工程军队重点实验室,武汉 430033)

3)(海军工程大学动力工程学院,武汉 430033)

离散发热器件基于火积耗散率最小和最高温度最小的构形优化比较∗

王刚1)2)3)谢志辉1)2)3)范旭东1)2)3)陈林根1)2)3)†孙丰瑞1)2)3)

1)(海军工程大学热科学与动力工程研究室,武汉 430033)

2)(海军工程大学舰船动力工程军队重点实验室,武汉 430033)

3)(海军工程大学动力工程学院,武汉 430033)

构形理论,火积耗散极值原理,电子器件冷却,广义热力学优化

建立了导热基座上圆柱体离散发热器件的三维湍流散热模型,基于构形理论,考虑空气变物性及可压缩性和黏性耗散,研究了器件材料的热导率、热源强度和流体流速对器件最高温度、基于火积耗散定义的当量热阻和平均Nu数的影响.结果表明:在总发热功率一定的条件下,以器件最高温度和当量热阻为性能指标进行热设计,均存在最优热源强度分布使得散热性能最优.当各热源强度相同且热源热导率小于基座热导率时,提高热源热导率可明显改善散热性能;将热源热导率沿流动方向从低到高布置可降低器件最高温度,而将热源热导率均匀布置可使当量热阻最小.所得结果可为实际热设计中不同材质和不同发热率的电子器件最优布置提供理论支撑.

1 引 言

随着电子器件功率和集成度的提高,电子器件冷却成为强化传热领域的研究热点.许多学者从强化传热手段、强化传热机理、强化传热原理和热优化设计等各个方面开展了广泛深入的研究[1−12].

构形理论为统一解释自然界各种流动系统结构形成的根本原因提供了理论基础[13−19],同时也为工程界各种流动系统的结构优化设计提供了统一的物理准则,被广泛应用于存在电子器件散热问题的热沉和热源(发热器件)的优化设计研究.热沉优化研究涉及空腔热沉、肋片热沉、通道热沉等,热源优化研究则主要分为热源分布优化和热源体优化.在热源分布优化方面,Bejan等[20]和Stanescu等[21]在强迫对流和自然对流条件下,给定热源总体积,分别以热流密度和换热系数最大化为目标获得了圆柱热源的最优间距.Jassim和Muzychka[22]建立了内置离散热源的变截面通道强迫对流换热模型,研究发现热源非均匀分布时冷却效果更佳.Hajmohammadi等[23,24]对外部包裹有肋片的热源进行了分布优化,发现一些新的分布方式比传统方式更有利于热源散热.Pedrotti等[25]在给定热源分布最大范围的约束下,以传热率最大化为目标,得出了优于热源顺排和叉排布置的离散热源分布方式.Shi和Dong[26]以峰值温度最低和流动阻力耗散最小化为目标,给定总散热率和长度约束,得出了热源在平板上的最优分布方式.Singh和Singh[27]则在开口空腔的左侧壁面布置一个热源,给定热源强度和空腔深度,在考虑热辐射的条件下,研究发现将热源布置在空腔壁上方可强化系统散热.范旭东等[28,29]建立了导热基座上圆柱体单热源和多热源散热的三维模型,以最高温度最小化和熵产率最小化为目标进行了构形优化,发现多尺度分布以及变热源强度比单尺度等热源强度分布更优.在热源体构形优化方面,龚舒文等[30−33]以无量纲最大热阻最小化为目标,在换热系数均匀、自然对流和强迫对流3种传热条件下对包裹着圆柱肋片的恒截面和变截面圆柱体热源三维模型进行了优化设计,发现热源高度对热源散热有重要影响,且变截面热源比恒截面热源的散热性能更优.

过增元[34]提出的火积理论奠定了传热学新的理论基础,形成了传热优化的新视角、新准则和新方法[35−39].Cheng等[40]用火积描述孤立系统的热平衡状态.Hu等[41]提出了可用火积流和可用系统火积两个新概念,通过对比分析传热过程中熵与火积的有关概念,指出传热过程可以不必区分状态参数和过程参数.Cheng等[42]分别运用火积耗散极值原理和熵产生最小化原理优化矩形直肋,发现以熵产生最小化为目标在某些工况中并不能使其传热性能达到最优.赵甜和陈群[43]通过与力学概念的对比,指出火积的宏观物理意义是物体的热量在温度场中的势能.程雪涛和梁新刚[44]讨论了火积理论在热功转化过程中的应用.Liu等[45]推导了基于火积概念的能量平衡方程,研究发现火积耗散极值原理比熵产生最小化原理更适用于封闭腔内的对流传热优化.还有一大批学者在导热问题[46]、对流换热问题[47,48]、热辐射问题[49]、传质问题[50,51]、换热器设计等[52,53]方面开展了广泛深入的研究,显示了火积理论的科学性和优势.

将构形理论与火积理论相结合,是传热优化的新方向[18,36,39].Wei等[54]最早将火积耗散极值原理与构形理论相结合应用于体点导热问题研究.Chen等[18,36,39,55,56]针对各种传热传质过程与部件开展了构形优化并拓展应用于钢铁生产流程优化.Xie等[57,58]基于有限元法对空腔和肋片开展了火积耗散率最小构形优化.Feng等[59]研究了微纳米尺度下的导热构形优化.龚舒文等[29−31]、范旭东等[32,33]针对热源体及其分布的优化问题,以当量热阻最小化为目标,开展了构形优化研究,结果表明,当量热阻最小的热源最优构形具有更好的整体传热性能.

综上所述,热源体的构形优化研究尚不多见,且一般是从几何结构角度进行优化并分析热导率、流体流速等物理条件的影响,鲜有考虑常见的电子器件热源热导率和发热功率不同时的最佳配置问题.在文献[29—33]的基础上,本文考虑实际电子器件的热导率和发热功率不同,建立导热基座上等尺寸的圆柱体离散发热器件三维湍流散热模型,基于构形理论和火积耗散极值原理,研究不同流速下热源热导率和热源强度分布的最优构形设计,并与最高温度最小化的优化结果进行比较分析,所得结果可为实际电子器件热设计提供理论支撑.

2 热源模型及数值方法

2.1 几何模型

热源散热的几何模型如图1所示,整个计算域为一长方体区域,其长、宽、高分别为L,W和H(数值分别为400,100,103 mm),矩形平板基座厚度Hb=3 mm,基座上布置有4个尺寸相等的离散热源(沿流体流动方向依次编号),其中热源直径d=30.9 mm,热源高度Hs=20 mm,前后端的热源与前后边缘的距离均为L0=40 mm,相邻热源中心轴的距离均为Ls=96.37 mm.

图1 热源几何模型Fig.1.Geometric model of heat source.

2.2 传热模型

模型基座材料为硅(定压比热容cp,b为700 J·kg−1·K−1, 密度ρb为2329 kg·m−3, 热导率λb为130 W·m−1·K−1). 冷却介质为洁净空气,假设空气流动为可压缩稳态湍流流动,考虑空气的变物性和黏性耗散,通道壁面采用无滑移边界条件,通道边界及基座底面为绝热面.气流入口速度垂直于入口端面,温度为293.15 K.

空气流动的连续性方程、动量方程、能量方程、湍动能方程、湍流耗散率方程和湍流黏度方程所组成的时均方程组为[60]

式中ρ为流体密度(kg·m−3),U为速度矢量(m·s−1),p为压力(Pa),I为单位矩阵,F为体积力(N·m−3),T为温度(K),q为热流矢量(W·m−2),µ为分子黏性系数(Pa·s),µT为湍流黏性系数(Pa·s),k和ε分别为湍动能(m2·s−2)和湍流耗散率(m·s−3),cp为流体的定压比热容(J·kg−1·K−1),Q为包含黏性耗散和压力功在内的热源项(W·m−3),Pk为湍动能的生成项(kg·m−2·s−3);Cε1,Cε2,Cµ,σk,σε均为经验常数,取值分别为:Cε1=1.44,Cε2=1.92,Cµ=0.09,σk=1,σε=1.3.

常物性固体基座稳态导热的能量方程为

常物性热源稳态导热的能量方程为

式中q′′′为热源强度(W·m−3),λs为热源热导率(W·m−1·K−1).

热源总发热率和热源总热导率作为约束条件给定.

2.3 性能指标

分别以器件当量热阻Rh和最高温度Tmax为性能指标开展优化研究.最高温度越低,系统越不容易被烧蚀;当量热阻越小,系统的整体传热性能越优.

传热过程的火积耗散率为[34,35]

式中λ为物质的热导率(W·m−1·K−1).

当量热阻定义为[34,35]

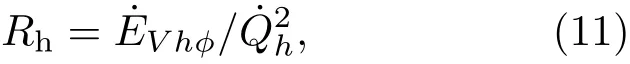
整个散热系统(基座、热源和气流)的火积耗散率为

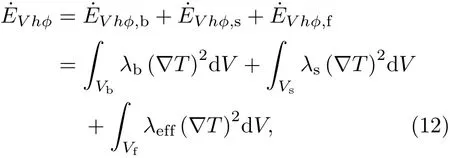
故散热系统的当量热阻为

2.4 数值方法

控制方程和边界条件采用有限元计算软件COMSOL Multiphysics求解,选用标准k-ε湍流模型.对流体和固体区域均进行四面体剖分,为保证计算精度,对网格独立性进行了检验.采用数量分别为264761,513869和1382375的3套网格试算,在流体流速U=3 m·s−1、等热源强度且等热导率的情况下,得出圆柱体热源的最高温度分别为370.05,372.12,372.20 K,相对误差分别为0.56%和0.02%.为兼顾计算精度和效率,计算选用第二套网格的划分策略.方程求解过程的收敛标准统一为1×10−6.

3 结果与讨论

3.1 热源强度对散热性能的影响

各热源的热源强度沿气流方向分别为,且按等差关系分布,即

式中Δq′′′为热源强度差(W·m−3).

考虑到热源总发热功率的约束,各热源强度值为(部分热源强度值见表1)

表1 各热源的热源强度 (单位:105W·m−3)Table 1.The intensity of each heat source(in 105W·m−3).

图2—图4所示为热源热导率一定时,热源强度差Δq′′′对器件最高温度Tmax、当量热阻Rh和平均Nu数的影响.

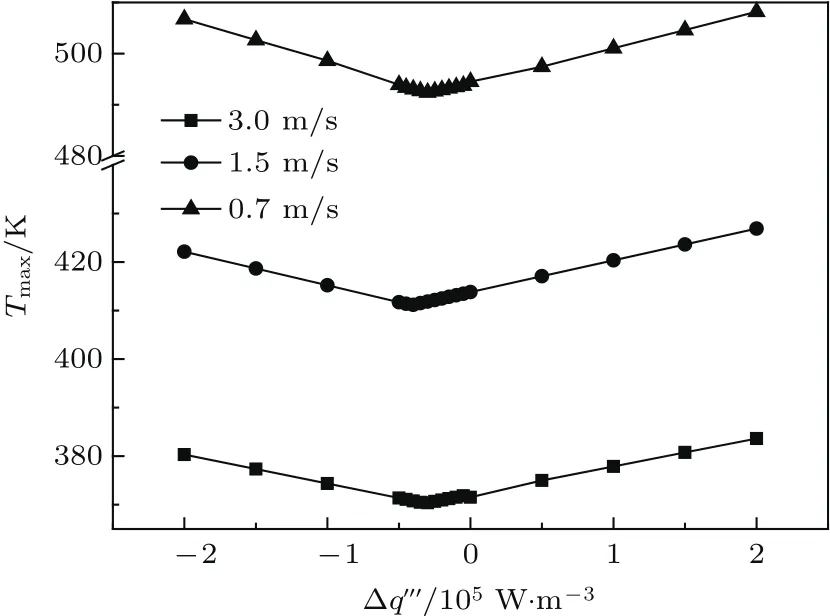
图2 Δq′′′对Tmax的影响Fig.2.The in fl uence of Δq′′′on Tmax.

由图2和图3可知,随着热源强度差Δq′′′的增大,器件最高温度Tmax和当量热阻Rh均先减小后增大,存在最优热源强度差使得Tmax和Rh最小.计算表明,在不同的流体流速条件下,同一优化目标下的是不同的;同一流速条件下,对应最高温度最小值和当量热阻最小值的也不完全相同.表2列出了不同流速下的最优热源强度分布及性能指标值,表中和分别为以Tmax和Rh为性能指标时的最优热源强度差.

图3 Δq′′′对Rh的影响Fig.3.The in fl uence of Δq′′′on Rh.

图4 Δq′′′对的影响Fig.4.The in fl uence of Δq′′′on

同时,综合图2—图4可知,器件最高温度和当量热阻均随流体流速的增大而减小,随流体流速的增大而增大.

表2 不同流速下的最优热源强度分布及性能指标值Table 2.The optimal distribution of heat source intensities and the performance values at different fl uid flow rates.

图5所示为U=0.7 m·s−1时热源的温度梯度云图.由图可知,随着热源强度差的不断增大,热源强度沿流动方向由从大到小排列向从小到大排列转变,温度梯度由沿流动方向减小逐渐变为均布在各热源周围.

图5 (网刊彩色)器件的温度梯度云图(U=0.7 m·s−1)(a) Δq′′′ = −2 × 105W·m−3;(b) Δq′′′ = −0.3 ×105W·m−3;(c) Δq′′′=2 × 105W·m−3Fig.5.(color online)Temperature gradient nephograms of the components(U=0.7 m·s−1):(a) Δq′′′= −2 ×105W·m−3;(b) Δq′′′= −0.3 × 105W·m−3;(c) Δq′′′=2×105W·m−3.

由图5(a)可知,当Δq′′′=−2×105W·m−3时,虽然热源强度和温度梯度均沿流动方向减小,但入口处热源强度相对过大,使得靠近入口处的热源冷却欠佳,因此最高温度和当量热阻均较高. 由图5(b)可知,当Δq′′′=−0.3×105W·m−3时,沿着流体流动方向,热源附近的温度梯度逐渐变小,热源强度逐渐变小,最好地兼顾了各个热源的冷却,故最高温度和当量热阻均最低;当Δq′′′=2×105W·m−3时,4个热源附近的温度梯度基本相等,但沿着流体流动方向,热源强度逐渐增大,这导致靠近出口处热源的冷却欠佳.综合U=0.7,1.5,3.0 m·s−1时的计算结果可知,不同优化目标下的最优热源强度差对应热源强度分布与温度梯度分布的最佳匹配,对相应优化目标而言,此时各热源的冷却均得到最佳兼顾,散热负荷大的地方也是对流换热能力强的地方,全场散热最好.

由此可见,在实际热设计中,存在最佳的热源强度分布使得系统的散热性能最优;热源强度越高的热源应距通道入口处更近一些,同时流体流速对热源强度的最优分布有一定影响;热源强度高的热源更靠近出口可增大平均Nu数,即增强对流换热,但流体流速越小,增强效果越弱.

3.2 热导率对散热性能的影响

图6 λs对Tmax的影响Fig.6.The in fl uence of λson Tmax.

图7 λs对Rh的影响Fig.7.The in fl uence of λson Rh.

图6 和图7分别为各热源的热源强度和热源热导率均相等时,热源材料的热导率λs对器件最高温度Tmax和当量热阻Rh的影响.从图中可看出,对三种流速情况,随着热源热导率λs的增加,器件最高温度和当量热阻均逐渐下降,且当热源热导率小于基座热导率(130 W·m−1·K−1)时,曲线下降较快,当热源热导率大于基座热导率时,下降变缓,当热导率λs达到400 W·m−1·K−1时,曲线已基本趋于平缓.这是由于当热导率增加到一定程度时,热源体的温度已接近其表面温度,此时提高热导率已难以改善系统散热性能.可见,在实际热设计中,适当提高热源材料的热导率可以强化散热,且当热源热导率比较低时改善效果更加明显.

为了便于研究各热源热导率不等的情况,设各热源的热导率沿流体流动方向分别为λs,1,λs,2,λs,3和λs,4,且按等差分布,即

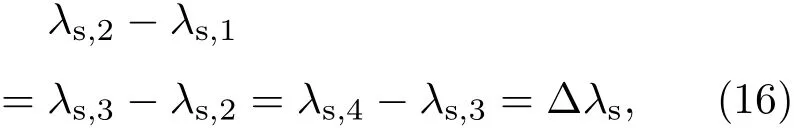
式中Δλs为热源热导率差(W·m−1·K−1).

考虑到热源总热导率和实际材料热导率的约束,假设热源热导率满足(部分热源热导率值见表3)

图8和图9为热源强度一定时,热源热导率沿流动方向按等差数列分布对系统散热性能的影响.由图8可知,器件最高温度Tmax随着热源热导率差Δλs的增大而减小,且减幅逐渐变小.可见,将热源热导率沿着流体流动方向按照从小到大的规律进行设置更有利于降低热点温度,提高系统的安全性.

表3 各热源的热导率 (单位:W·m−1·K−1)Table 3.The heat conductivities of heat sources(in W·m−1·K−1).

图8 λs分布方式对Tmax的影响Fig.8.The in fl uence of distribution of λson Tmax.

由图9可知,当量热阻Rh随着热源热导率差Δλs的增大先减小后增大,在Δλs=0时达到最小.即追求当量热阻最小化时,应使各热源热导率均相等,才能达到最优效果.综合图8和图9可知,器件最高温度和当量热阻均随流体流速的增加而减小.

图9 λs分布方式对Rh的影响Fig.9.The in fl uence of distribution of λson Rh.

4 结 论

本文建立了导热基座上等尺寸圆柱体离散热源的三维湍流散热模型,研究了热源材料的热导率、热源强度和流体流速对器件最高温度、基于火积耗散定义的当量热阻以及平均Nu数的影响.结果表明:分别采用器件最高温度和当量热阻作为性能指标,当系统总发热功率一定时,均存在最优热源强度分布使得系统散热性能达到最佳.在不同的流体流速条件下,同一优化目标下的最优热源强度分布是不同的;同一流速条件下,对应最高温度最小值和当量热阻最小值的最优热源强度分布也不完全相同.将热源强度沿流动方向按从大到小布置有利于使系统散热性能达到最优.当各热源的热源强度相同时,适当提高热源热导率有利于强化系统的散热效果.当热源材质不同时,应根据优化目标的不同,选择不同的热导率分布方式以获得相应的最优散热效果.本文结果可为电子器件实际热设计中不同材质和不同发热功率的单列离散热源最优布置提供理论支撑.不同工况下离散热源热点温度位置及大小的变化规律,以及全场平均的对流传热强化与离散热源最佳冷却效果之间的关系值得进一步深入研究.

[1]Guo Z Y,Li D Y,Wang B X 1998Int.J.Heat Mass Transfer41 2221

[2]Tao W Q,Guo Z Y,Wang B X 2002Int.J.Heat Mass Transfer45 3849

[3]Xuan Y M 2014Sci.China Tech.Sci.44 269(in Chinese)[宣益民2014中国科学:技术科学44 269]

[4]Chen L G,Meng F K,Sun F R 2016Sci.China Tech.Sci.59 442

[5]Chen Y P,Yao F,Shi M H 2012Int.J.Heat Mass Transfer55 4476

[6]Xie G N,Liu J,Liu Y Q,Sunden B,Zhang W H 2013Trans.ASME J.Electron.Packag.135 021008

[7]Zhao D L,Tan G 2014Appl.Thermal Eng.66 15

[8]Kang N,Wu H Y,Xu F Y 2015J.Engng.Thermophys.36 1572(in Chinese)[康宁,吴慧英,徐发尧 2015工程热物理学报36 1572]

[9]Green C,Kottke P,Han X F,Woodrum C,Sarvey T,Asrar P,Zhang X C,Joshi Y,Fedorov A,Sitaraman S,Bakir M 2015J.Electron.Packag.137 040802

[10]Luo X B,Hu R,Liu S,Wang K 2016Prog.Energ.Combust.Sci.56 1

[11]Chen K,Wang S F,Song M X 2016Int.J.Heat Mass Transfer93 108

[12]Zhang X C,Han X F,Sarvey T E,Green C E,Kottke P A,Fedorov A G,Joshi Y,Bakir M S 2016J.Electron.Packag.138 010910

[13]Bejan A 1997Int.J.Heat Mass Transfer40 799

[14]Bejan A 2000Shape and Structure,from Engineering to Nature(Cambridge:Cambridge University Press)pp1–314

[15]Bejan A,Lorente S 2008Design with Constructal Theory(New Jersey:Wiley)pp1–62

[16]Chen L G,Feng H J 2016Multi-objective Constructal Optimization for Flow and Heat and Mass Transfer Processes(Beijing:Science Press)pp1–23(in Chinese)[陈林根,冯辉君2016流动和传热传质过程的多目标构形优化(北京:科学出版社)第1—23页]

[17]Bejan A 2016The Physics of Life:The Evolution of Everything(New York:St.Martin’s Press)pp1–27

[18]Chen L G 2012Sci.China Tech.Sci.55 802

[19]Bejan A,Errera M R 2016J.Appl.Phys.119 074901

[20]Bejan A,Fowler A J,Stanescu G 1995Int.J.Heat Mass Transfer38 2047

[21]Stanescu G,Fowler A J,Bejan A 1996Int.J.Heat Mass Transfer39 311

[22]Jassim E,Muzychka Y S 2010J.Heat Transfer132 011701

[23]Hajmohammadi M R,Poozesh S,Nourazar S S 2012Proc.IMechE Part E J.Process Mech.Eng.226 324

[24]Hajmohammadi M R,Poozesh S,Nourazar S S,Manesh A H 2013Mech.Sci.Tech.27 1143

[25]Pedrotti V A,Souza J A,Isoldi J A,dos Santos E D,Isoldi L A 2015Engenharia Termica(Thermal Engineering)14 16

[26]Shi Z Y,Dong T 2015Energ.Convers.Manage.106 300

[27]Singh D K,Singh S N 2015Int.J.Heat Mass Transfer89 444

[28]Fan X D,Xie Z H,Sun F R,Yang A B 2016J.Eng.Therm.37 1994(in Chinese)[范旭东,谢志辉,孙丰瑞,杨爱波2016工程热物理学报37 1994]

[29]Fan X D 2015M.S.Thesis(Wuhan:Naval University of Engineering)(in Chinese)[范旭东 2015硕士学位论文(武汉：海军工程大学)]

[30]Gong S W,Chen L G,Feng H J,Xie Z H,Sun F R 2015Int.Commun.Heat Mass Transfer68 1

[31]Gong S W,Chen L G,Feng H J,Xie Z H,Sun F R 2014Chinese Sci.Bull.59 3609(in Chinese)[龚舒文,陈林根,冯辉君,谢志辉,孙丰瑞2014科学通报59 3609]

[32]Gong S W,Chen L G,Feng H J,Xie Z H,Sun F R 2016Sci.China Tech.Sci.59 631

[33]Gong S W 2014M.S.Thesis(Wuhan:Naval University of Engineering)(in Chinese)[龚舒文 2014硕士学位论文(武汉：海军工程大学)]

[34]Guo Z Y,Zhu H Y,Liang X G 2007Int.J.Heat Mass Transfer50 2545

[35]Li Z X,Guo Z Y 2010Field Synergy Principle of Heat Convection Optimization(Beijing:Science Press)pp78–97(in Chinese)[李志信,过增元2010对流传热优化的场协同理论(北京:科学出版社)第78—97页]

[36]Chen L G 2012Chinese Sci.Bull.57 4404

[37]Chen Q,Liang X G,Guo Z Y 2013Int.J.Heat Mass Transfer63 65

[38]Cheng X T,Liang X G 2014Chinese Sci.Bull.59 5309

[39]Chen L G 2014Sci China Tech.Sci.57 2305

[40]Cheng X T,Liang X G,Guo Z Y 2011Chinese Sci.Bull.56 847

[41]Hu G J,Cao B Y,Guo Z Y 2011Chinese Sci.Bull.56 2974

[42]Cheng X T,Zhang Q Z,Xu X H,Liang X G 2013Chin.Phys.B22 020503

[43]Zhao T,Chen Q 2013Acta Phys.Sin.62 234401(in Chinese)[赵甜,陈群2013物理学报62 234401]

[44]Cheng X T,Liang X G 2014Acta Phys.Sin.63 190501(in Chinese)[程雪涛,梁新刚 2014物理学报 63 190501]

[45]Liu W,Liu Z C,Jia H,Fan A W,Nakayama A 2011Int.J.Heat Mass Transfer54 3049

[46]Wang H G,Wu D,Rao Z H 2015Acta Phys.Sin.64 244401(in Chinese)[王焕光,吴迪,饶中浩2015物理学报64 244401]

[47]Chen G M,Tso C P 2012Int.J.Heat Mass Transfer55 3744

[48]Jia H,Liu Z C,Liu W,Nakayama A 2014Int.J.Heat Mass Transfer73 124

[49]Wu J,Cheng X 2013Int.J.Heat Mass Transfer58 374

[50]Yuan F,Chen Q 2012Chinese Sci.Bull.57 687

[51]Zheng Z J,He Y L,Li Y S 2014Sci.China Tech.Sci.57 773

[52]Xia S J,Chen L G,Sun F R 2009Chinese Sci.Bull.54 3587

[53]Guo J F,Huai X L,Li X F,Cai J,Wang Y W 2013Energy63 95

[54]Wei S H,Chen L G,Sun F R 2008Sci.China Ser.E Tech.Sci.51 1283

[55]Chen L G,Feng H J,Xie Z H 2016Entropy18 353

[56]Chen L G,Yang A B,Xie Z H,Feng H J,Sun F R 2017Int.J.Therm.Sci.111 168

[57]Xie Z H,Chen L G,Sun F R 2009Sci.China Ser.E Tech.Sci.52 3504

[58]Xie Z H,Chen L G,Sun F R 2009Chinese Sci.Bull.54 4418

[59]Feng H J,Chen L G,Xie Z H,Sun F R 2016J.Energy Inst.89 302

[60]COMSOL 2012COMSOL Multiphysics User’s Guide(Version 4.3b)(Sweden: COMSOL Incorporated)pp103–147

Comparative studies on constructal optimizations of discrete heat generation components based on entransy dissipation minimization and maximum temperature minimization∗

Wang Gang1)2)3)Xie Zhi-Hui1)2)3)Fan Xu-Dong1)2)3)Chen Lin-Gen1)2)3)†Sun Feng-Rui1)2)3)

1)(Institute of Thermal Science and Power Engineering,Naval University of Engineering,Wuhan 430033,China)
2)(Military Key Laboratory for Naval Ship Power Engineering,Naval University of Engineering,Wuhan 430033,China)
3)(College of Power Engineering,Naval University of Engineering,Wuhan 430033,China)

4 April 2017;revised manuscript

22 May 2017)

A three-dimensional(3D)turbulent heat dissipation model of cylindrical discrete heat generation components is established on a conductive basis.The whole solid section is set in a square channel with adiabatic walls,and the components,cooled by clean air fl owing through the channel,are arranged in a line with equal spacings.The in fl uences of the heat conductivities of the components,intensities of heat sources and velocity of fl uid fl ow on the maximum temperature(MT)of components,the equivalent thermal resistance(ETR)based on entransy dissipation of the heat dissipation system,and the averagedNunumber are investigated with the constructal theory considering variable properties,compressibility and viscous dissipation of air.The total heat generation rate and the total heat conductivity of heat sources are fi xed as the constraint conditions.The circumstances in which heat generation rates and heat conductivities of heat sources are unequal are considered.The results show that for the fi xed total heat generation rate of heat sources,despite MT or ETR that is taken as the performance index for thermal design,there exists an optimal intensity distribution of heat sources for the best thermal performance of the system.In fact,for different objectives,the optimal intensity distributions of heat sources are corresponding to the best match between the distributions of heat sources and the distributions of temperature gradient.There are different optimal distributions for different velocities of the fl uid fl ow and different optimization objectives.Besides,the averagedNunumber increases with the increase of intensity di ff erence in heat sources,which means that the convective heat transfer is enhanced,but this phenomenon is relatively weak when the velocity of fl uid fl ow is low.For the fi xed total heat generation rate of heat sources,when the intensities of heat sources are equal and the thermal conductivities of heat sources are lower than that of the conductive basis,increasing heat conductivities of the heat sources can evidently improve thermal performance of the system;the MT can be lowest when the conductivities of heat sources increase along the fl uid fl ow;and the ETR is lowest when the conductivities of heat sources are equal.Both the MT and the ETR decrease with the increasing velocity of fl uid fl ow.The results can provide some theoretical guidelines for the practical thermal design of the electronic components with different materials and different heat generation rates.

constructal theory,entransy dissipation extremum principle,cooling of electronic components,generalized thermodynamic optimization

(2017年4月4日收到;2017年5月22日收到修改稿)

10.7498/aps.66.204401

∗国家自然科学基金(批准号:51579244,51206184)和海军工程大学自主立项课题(批准号:20160134)资助的课题.

†通信作者.E-mail:lingenchen@hotmail.com

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

PACS:44.27.+g,44.10.+i,05.70.CeDOI:10.7498/aps.66.204401

*Project supported by the National Natural Science Foundation of China(Grant Nos.51579244,51206184)and the Independent Project of Naval University of Engineering(Grant No.20160134).

†Corresponding author.E-mail:lingenchen@hotmail.com