基于小波变换的低位赋值盲水印算法
2017-11-10蔡伟琦
蔡伟琦
(集美大学诚毅学院 福建厦门 361021)
基于小波变换的低位赋值盲水印算法
蔡伟琦
(集美大学诚毅学院 福建厦门 361021)
针对版权认证的安全性和鲁棒性要求,提出一种基于离散小波变换的低位赋值盲水印算法。该算法将水印信息经过小波变换后,通过图像置乱和数值转化,将符合要求的数据循环赋值到彩色图像小波分解后低频分量的低位数上。该算法具有不可见性,并利用图像置乱加了一道安全防线。大量的仿真攻击和模拟结果表明,该算法对噪声、滤波、压缩、裁剪等各种图像攻击具有较强的抵抗能力,算法具有较好的鲁棒性。
鲁棒性;小波变换;低位赋值;图像置乱
数字水印技术,是指用信号处理的方法在数字化的多媒体数据中嵌入隐蔽的标记,用以证明原创作者对其作品的所有权,并作为鉴定起诉非法侵权的证据。这种标记通常是不可见的,是实现版权保护的有效办法,同时通过对水印的探测和分析,能够保证数字化信息的完整性和可靠性,从而成为知识产权保护和数字多媒体防伪的有效手段。近年来,针对图像处理的数字水印技术研究取得了很大进步,主要分为空域算法和变换域算法两类,变换域算法中离散小波变换(DWT)因其良好的空间频域局部化特性与人眼视觉特性相符的变换机制,成为数字水印技术的研究热点。目前已有许多基于DWT的图像水印算法,文献[1]提出一种基于DWT将水印嵌入到YIQ色彩空间中的Y和Q分量;文献[2][4]研究了基于小波变换的零水印技术;文献[5][6]进行了基于人类视觉特性HVS的小波域水印算法研究。这些算法的算法复杂度均较高,计算较复杂。鉴于此,本文结合DWT提出一种基于图像低频数据进行低位赋值的算法,能方便实现水印的盲提取,鲁棒性好,有利于硬件的实现。
一、图像的小波分解
波分析方法是一种窗口大小固定但其形状可以改变,即时间窗和频率窗都可以改变的时频局域化分析方法,基于小波变换的多尺度图像分析可以将图像在不同尺度的频率上进行分解和重构。对于二维离散图像信号,经过一级DWT变换后,图像被分解成四个分量:一个低频子图LL和三个高频子图:水平子图LH、垂直子图HL和对角子图HH。下一级DWT变换在前级产生的LL基础上进行,依次重复,可完成图像的n级小波分解,得到图像的n级分辨率,整个图像的能量主要集中在最低频子图上。小波合成过程与分解过程恰好相反。图1是图像二级小波变换的分解过程。
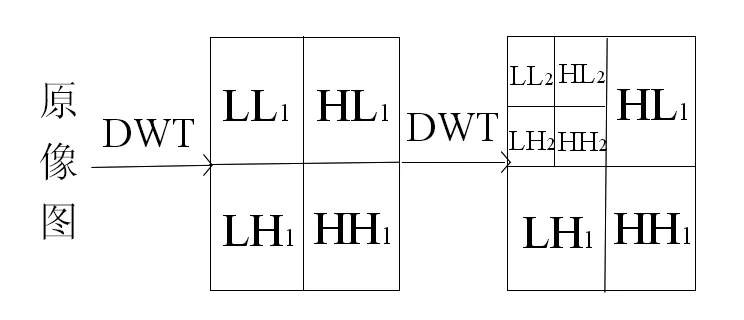
图1 图像的二级小波分解
实际上,利用小波变换进行水印数据的嵌入和提取,必然经过多次的数据分解和合成,若对图像的分解层级太多将不可避免引起数据变化和失真,而层级太少会导致图像处理的鲁棒性较差。同时,图像还要能够抵御外来的各种攻击,如噪声、滤波、压缩、裁剪等,在攻击后还要能顺利恢复出水印数据,这就要求水印嵌入和提取的算法鲁棒性强,也要具备一定的保密性。
本文基于Haar离散小波变换,对原载体图像进行Haar二级小波分解,对水印图像进行Haar一级小波分解。Haar小波变换可以方便地对信号的高、低频子图数据进行分析,必要时可以忽略微不足道的细节系数,很适合在水印技术上应用,也为水印的快速重构提供了一种途径。
二、水印算法描述
从视觉角度来看,低频子图是原始图像的平滑逼近,抗干扰能力强,图像的主能量主要集中在低频子图上,而高频子图反映的是图像的变化部分,是细节图像,抗干扰能力较弱。为增强水印算法的鲁棒性,本文选择把水印图像的信息嵌入到原载体图像的低频子图数据中。由于低频数据的敏感性,嵌入算法尤为重要,要保证原载体图像嵌入水印后图像质量不下降。本文提出一种算法,利用低频子图数据的取值特点采用低位赋值的方法方便有效地嵌入和恢复水印数据。
(一)水印嵌入算法。水印通常并不是内容非常丰富的图像,在不影响对水印辨认识别的情况下,仅由其低频子图数据足以重建整个图像。将水印图像进行小波分解后,只需将水印的低频子图数据隐藏到原载体图像,不考虑其高频子图部分,水印的提取也只需提取出水印的低频子图数据即可。同时,为提高水印数据的保密性,增强水印的鲁棒性,通过Arnold变换将水印图像置乱,利用Arnold变换的周期性,在恢复水印过程中经有限次迭代可重新得到原水印[7]。
原载体图像是M×N的真彩色图像,由R、G、B三基色构图而成,每像素的比特数通常取8,即像素灰阶数为256。它的数据矩阵集合 {A}是M×N×3的三维矩阵,可分解成{AR}、{AG}、{AB}三个独立的M×N二维矩阵。分别对三个矩阵{AR}、{AG}、{AB}进行二级小波分解,得到二级小波变换下的三组数据{BR}、{BG}、{BB},数据长度均为M×N。
根据小波分解的原理,{BR}、{BG}、{BB}中前1/4的数据分别构成原载体图像的R、G、B低频子图LL1,前1/16的数据分别构成LL2,记为{CR}、{CG}、{CB},其中,
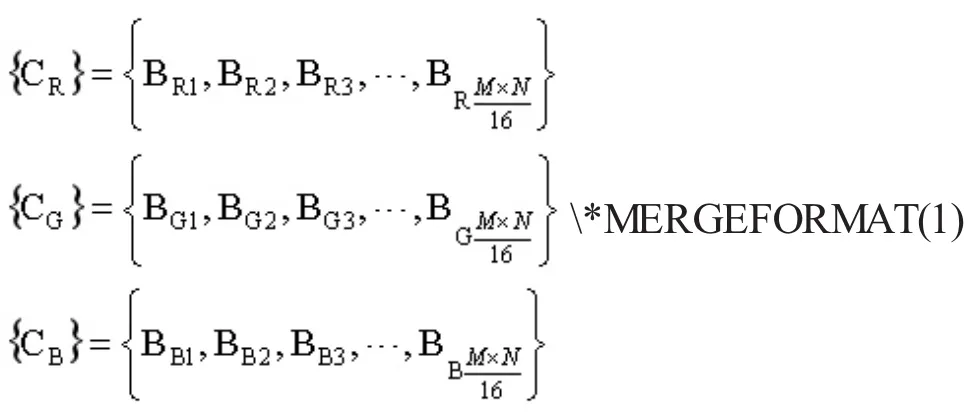
{CR}、{CG}、{CB}是原载体图像的R、G、B二级低频子图数据。根据Haar离散小波变换采用的运算规则,通常标准化Haar小波分解滤波器下的低通滤波器系数均为对像素灰阶数为256的二维真彩色图像而言,其低频数据的取值特点和小波分解的层级有关,n级小波分解后其低频子图数据的取值区间为:
鉴于低频子图数据的这个特点,本文对原载体图像低频数据的低位进行水印嵌入。将{CR}、{CG}、{CB}中的数据转换成等值二进制数,通过对二进制数低K位的适当取舍,舍去低K位后的数值,用经过处理的水印低频子图数据代替。
K=0时,即舍去二进制数据的小数部分;K=1时,舍去二进制数据的个位及其小数部分,也即舍去原十进制数据除以2得到的小数部分;依此类推,K=n时,舍去二进制数据的n位整数部分及其小数部分,也即舍去原十进制数据除以得到的小数部分。本文把K定义为“水印容度”,表示水印能够赋值在原载体图像上的二进制数据宽度。
可见,容度K越小时,对原载体图像的数据改动越小,嵌入水印后的图像和原载体图像的相似程度越高,然而不可避免地造成赋值在原载体图像上的水印数据宽度窄,嵌入水印的数值较小,影响到水印的精度,对水印的提取造成一定的困难。容度K越大时,赋值在原载体图像上的水印数据宽度将变大,更容易恢复出水印,但此时对原载体图像的数据改动较大,嵌入后的图像和原载体图像的相似程度变低。
为保证嵌入水印后原载体图像质量不下降以及水印能够顺利恢复,并具备一定的鲁棒性,通过对K的取值进行多次测试,K=3时能够达到一种最佳平衡,得到的算法更加合理有效,此时只要保证嵌入的水印数据小于8即可。由于水印图像只进行了Haar一级小波分解,因此水印低频数据的取值区间为[0,510],通过适当的数值转化限定在[0,8)是容易做到的(比如对数据开三次方)。另外,一般情况下,原载体图像的低频子图数据量比水印的低频数据量要大得多,为提高水印的抗攻击能力,把水印数据循环赋值给原载体图像。
嵌入算法的实现步骤:
第一步:读取任意尺寸的彩色载体图像,对载体图像进行离散小波变换,得到其低频子图数据;
第二步:读取任意方形尺寸的彩色水印图像,对水印图像进行离散小波变换,得到其低频子图数据;
第三步:将得到的水印低频子图数据进行Arnold置乱;
第四步:设定水印容度K=3,对原载体图像和水印的低频子图数据分别进行数据处理,在原载体图像上循环嵌入水印数据;
第五步:对已嵌入水印的图像数据进行逆小波变换,获得含水印的图像。
(二)水印盲检算法。盲检算法是嵌入算法的逆运算。具体步骤如下:
第一步:读取含水印的图像数据,进行离散小波变换,得到其低频子图数据;
第二步:根据水印容度值对得到的低频子图数据进行处理,提取出其低位数据,组成水印图像的低频子图数据;
第三步:把第二步得到的数据进行还原,并经Arnold置乱恢复;
第四步:对恢复后的水印数据进行逆小波变换,获得原始水印图像。
三、实验仿真分析
为验证本文算法的综合性能,引入两个常用的图像评价指标:PSNR和NC。
PSNR(Peak signal to Noise Ratio),峰值信噪比,用于评价一幅经处理后的图像与原图像相比质量的好坏。PSNR的单位是dB,PSNR越高,失真越小。PSNR定义为:
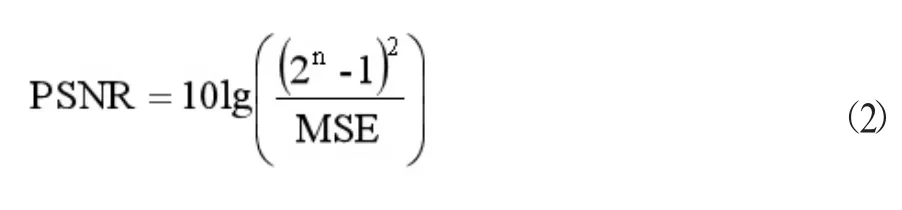
其中,n为每像素的比特数,一般取8,即像素灰阶数为256。MSE表示当前图像X和参考图像Y的均方误差(Mean Square Error),两幅M×N图像X、Y的MSE定义为:
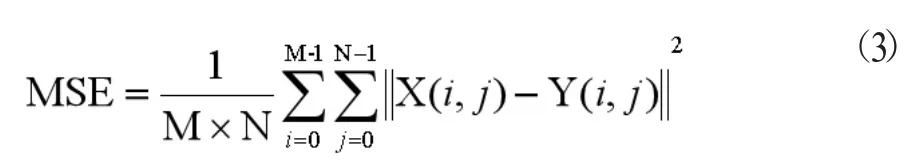
对于三基色R、G、B的真彩色图像,可分别计算R、G、B三通道的PSNR值或者计算每个通道的MSE值取平均,再得到PSNR。
PSNR是基于对应像素点间的误差,即基于误差敏感的图像质量评价,并未全面考虑到人眼的视觉特性,经常出现评价结果与人的主观感觉不一致的情况。目前针对图像的质量评价均存在主客观评价的差异,评价效果并不十分理想,本文采用PSNR主要是用来对提取水印的质量进行定量对比,同时引入另一个评价标准NC来度量图像的相似性。
NC(Normalized Cross-Correlation),归一化互相关函数,用来判定信号的相似性,是度量两张图片相似度的一种表示形式,NC越大代表两张图片的相似性越高。它的定义为:
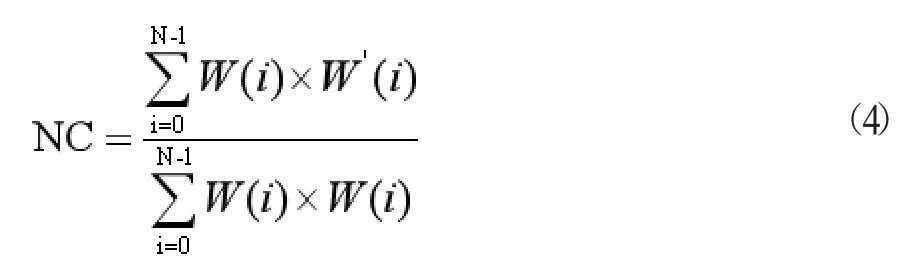
其中,N是图像信息长度,W(i)是原始图像,W'(i)是经处理过的图像。
(一)水印嵌入和提取。本文采用尺寸为1600×900的彩色载体图像,128×128的24位真彩色水印图像。水印图像的“水印技术”分别为红(255,0,0)、绿(0,255,0)、蓝(0,0,255)、黑(0,0,0)组合,并采用分别计算R、G、B三通道PSNR值的方法,便于观察各种攻击对R、G、B三基色的影响。图2左图为原载体图像和原水印图像,右图为嵌入水印后的图像和提取出的水印。

图2 水印的嵌入和提取
嵌入水印后的图像质量未明显降低,说明该算法具有不可见性。采用PSNR、NC评价嵌入水印后的图像质量。NC=0.9999;PSNR(R)=52.17dB,PSNR(G)=52.21dB,PSNR(B)=52.17dB,确认该嵌入算法有效。
对比原水印,提取出的水印图像质量略微下降,但几乎不影响水印的检测和识别,经计算两者的NC=0.9947,PSNR (R)=26.64dB,PSNR(G)=26.41dB,PSNR(B)=27.02dB,表明算法对R、G、B三基色的影响程度较一致,视觉上也证明了这一点。该算法恢复的水印可鉴别,算法整体有效。
为进一步检测算法的性能,考察几种常见的针对图像的攻击,包括噪声、滤波、JPEG压缩和几何攻击等,进行鲁棒性测试。
(二)噪声攻击。用不同强度的椒盐噪声或高斯噪声对已嵌入水印的图像进行攻击后,利用盲检算法恢复水印,验证算法的有效性。
1.椒盐噪声。向图像加入椒盐噪声,恢复的水印是椒盐噪声密度为0.05时的结果,见图3。由图可见,椒盐噪声对R、G、B三基色的影响程度区别不大,但原本白色的背景已被底噪所覆盖,导致PSNR数值急剧下降。恢复的水印和原水印两者的 NC=0.9526,PSNR(R)=16.53dB,PSNR(G)=16.21dB,PSNR(B)=16.02dB。PSNR取值仍在可接受的范围。曲线图是椒盐噪声密度在0-0.2范围内NC和PSNR的变化曲线。

图3 水印恢复及NC和PSNR变化曲线(椒盐噪声)
2.高斯噪声。向图像加入高斯噪声,恢复的水印是加入均值0,方差0.001高斯噪声时的结果,见图4。可见,高斯噪声的底噪比椒盐噪声更深,虽暂未影响到对水印结果的辨识,但字体的颜色已有变化。此时NC=0.9241,PSNR(R)=8.94dB,PSNR(G)=8.92dB,PSNR(B)=9.04dB,比起椒盐噪声均有显著下降。得到的PSNR值已很不理想,但由于主客观评价存在一定的差异,水印主观上仍在可识别的范围。曲线图是均值0,方差在0-0.01范围内NC和PSNR的变化曲线。

图4 水印恢复及NC和PSNR变化曲线(高斯噪声)
(三)滤波攻击。
1.高斯滤波。利用高斯滤波对图像进行平滑处理,恢复的水印是校验矩阵5×5,高斯滤波参数s=0.5时的结果,见图5。高斯滤波对水印的识别影响并不大,R、G、B三色的辨识度足够清晰,白色的背景依然被底噪所覆盖,此时NC=0.9671,PSNR(R)=15.32dB,PSNR(G)=15.77dB,PSNR(B)=15.99dB。PSNR取值在可接受的范围。曲线图是高斯滤波参数在0.1-2范围内NC和PSNR的变化曲线。
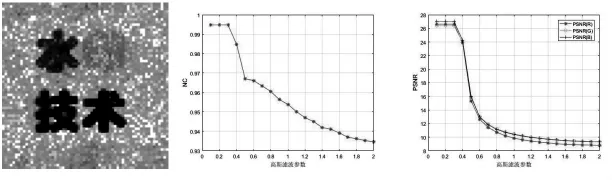
图5水印恢复及NC和PSNR变化曲线(高斯滤波)
2.中值滤波。对图像进行中值滤波,恢复的水印是处理窗口3×3时的结果,见图6。中值滤波对水印的识别产生了一定影响,虽水印仍可识别,R、G、B三色的辨识度已有所模糊,底噪更深,此时NC=0.9651,PSNR(R)=11.68dB,PSNR(G)=12.25dB,PSNR(B)=12.23dB。得到的PSNR值虽不理想,但色彩、字型上仍能明显识别。曲线图是中值滤波窗口从1×1到10×10 NC和PSNR的变化曲线。

图6 水印恢复及NC和PSNR变化曲线(中值滤波)
(四)JPEG压缩攻击。对图像进行JPEG压缩攻击,恢复的水印是质量因素为90时的结果,见图7。JPEG压缩攻击对水印色彩产生了较大影响,已几乎无法辨识三基色,但字体仍可识别,轮廓也足够清晰,底噪很大。此时NC=0.9296,PSNR(R)=8.03dB,PSNR(G)=10.11dB,PSNR(B)=7.78dB。得到的PSNR值虽不理想,但字型仍可识别。曲线图是图像质量因素60-100范围内JPEG压缩的NC和PSNR变化曲线。
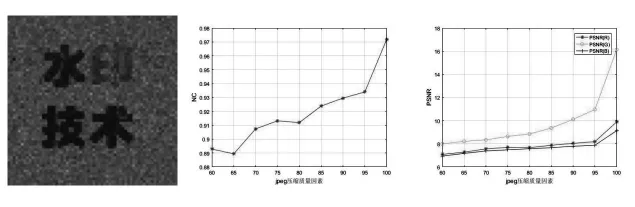
图7 水印恢复及NC和PSNR变化曲线(JPEG压缩)
(五)几何攻击。
1.裁剪攻击。将图像右半边部分裁掉,剩下原图的1/2,此时NC=0.9909,PSNR(R)=22.89dB,PSNR(G)=22.86dB,PSNR(B) =22.87dB。恢复的水印见图8左图,因算法进行了循环赋值,因而裁剪攻击对水印提取影响不大。
2.缩放攻击。先把图像缩小1/10,再恢复成原来大小,恢复出的水印见图8右图。底噪较深,字体颜色有部分变化。此时NC=0.9648,PSNR(R)=9.69dB,PSN(G)=9.91dB,PSNR(B)=9.95dB。得到的PSNR值并不理想,但主观上仍可识别。

图8 裁剪、缩放攻击下的水印恢复
四、结语
本文实现彩色图像嵌入彩色水印的低位赋值盲水印算法,提出了小波低频子图数据“水印容度”的概念,通过适当的“水印容度”进行数据取舍,实现盲检。
理论分析和仿真结果都表明,本算法抗噪能力强,对滤波、裁剪等攻击具备较强的鲁棒性,三基色对抗各种攻击的变化大体上一致,在遭受各种攻击后仍可以提取质量较高的水印。算法实现简单快速,视觉失真少,安全性较高,具有较强的实用性。
[1]guangmin sun,yao yu.DWT Based Watermar king Algorithm of Color Images[C].ICIEA,2007:1823-1826.
[2]杨树国,李春霞,孙枫,等.小波域内图象零水印技术的研究[J].中国图象图形学报,2003,8(6):664-669.
[3]吴胜兵,张定会,霍瑶,等.DWT系数分块的零水印方案[J].数据通信,2014(3):22-25.
[4]潘黄琼,陈光喜,丁勇,等.彩色图像DWT变换下的块SVD零水印[J].微电子学与计算机,2012,29(5):50-53.
[5]叶闯,沈益青,李豪,等.基于人类视觉特性(HVS)的离散小波变换(DWT)数字水印算法[J].浙江大学学报(理学版), 2013,40(2):152-155.
[6]武风波,汪峰.基于HVS的小波变换数字图像水印算法[J].应用光学,2014,35(2):254-259.
[7]丁玮,闫伟齐,齐东旭.基于Arnold变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001,13(4):338-341.
TP391
A
2095-0438(2017)11-0156-05
2017-06-12
蔡伟琦(1983-),男,福建厦门人,集美大学诚毅学院工程师,硕士,研究方向:通信技术,信号处理。
[责任编辑 郑丽娟]
