基于三轴X射线衍射方法的n-GaN位错密度的测试条件分析∗

何菊生 张萌 邹继军 潘华清 齐维靖 李平

1)(南昌大学科学技术学院,南昌 330029)

2)(南昌大学材料科学与工程学院,南昌 330031)

3)(核技术应用教育部工程研究中心(东华理工大学),南昌 330013)

4)(上饶职业技术学院机械工程系,上饶 334100)

5)(南昌大学现代教育技术中心,南昌 330031)

基于三轴X射线衍射方法的n-GaN位错密度的测试条件分析∗

何菊生1)†张萌2)邹继军3)潘华清4)齐维靖2)李平5)

1)(南昌大学科学技术学院,南昌 330029)

2)(南昌大学材料科学与工程学院,南昌 330031)

3)(核技术应用教育部工程研究中心(东华理工大学),南昌 330013)

4)(上饶职业技术学院机械工程系,上饶 334100)

5)(南昌大学现代教育技术中心,南昌 330031)

(2017年7月26日收到;2017年8月4日收到修改稿)

氮化镓,高分辨三轴X射线衍射,位错密度,晶界

1 引 言

对第3代半导体n-GaN材料位错密度的测试研究是半导体材料领域的重大课题.位错会降低载流子迁移率[1]、电子注入效率[2],造成器件漏电[3,4]等,对材料质量和器件性能产生许多不利影响.作为惟一非破坏性的方法,高分辨X射线三轴衍射(triple-axis X-ray di ff raction,TAXRD)法兼有免制样、操作简便等突出优点,并且该方法收集经过三轴晶(单色器、样品、分析器)布拉格衍射的信息,突出来自样品的信息[5],测试对晶格常数等参数具有极高的精确度,因此,TAXRD法是使用最为广泛,已成为主流测试技术之一.然而,晶粒尺寸效应加宽、翘曲加宽、位错加宽等众多因素都可能对半高全宽(FWHM)产生重大影响,导致位错密度测试可能极不准确.当前大量文献广泛报道了使用基于镶嵌结构模型的Srikant方法[6]或Williamson-Hall(W-H)方法[7−9]的实验研究,并未分离或剔除这些干扰加宽因素,且实验的准确性大多缺乏其他实验佐证.当然,也有不少TAXRD方法与透射电子显微镜(TEM)、化学腐蚀(EPD)等直观方法的实验对比研究报道[10−12].应该说,TEM方法测试的微区过小、并且位错分布可能横向、纵向很不均匀,EPD方法则腐蚀工艺难把握、腐蚀坑会重叠或不显现,都存在统计方面的瑕疵,难以作为比较标准.事实上,精确测量技术的发展方向是光学和电学测量,前者的高度精确性来源于干涉和衍射(衍射可看成是许多光源的干涉),后者则来源于数字信号技术.本文通过光学和电学测量,可以准确地解释晶粒尺寸效应(晶界)给纤锌矿n-GaN位错密度TAXRD测试带来的影响.

电学方法(霍尔迁移率曲线拟合)测试n-GaN位错密度,与TAXRD方法有很强的互补性.电学方法优点是测量精确度较高,一是因为测试灵敏;二是测试整个材料的平均位错密度;三是位错密度作为影响迁移率的重要因素,和其他因素能很好地整合到一起,理论和实验高度相符.电学方法也存在以下两方面缺点:一是操作环节较多,需要对衬底研磨减薄、切割、清洗、制作电极、变温测试等;二是对操作技术要求较高,常遇到欧姆接触不理想,以及抽真空等问题.因此,利用电学测试来改进TAXRD测试,是可行且必要的.

2 实验与原理

2.1 实验方法

对大量n-GaN样品的多个衍射面进行斜对称X射线ω扫描,从中选择两个特殊的样品,即全部对应晶面的FWHM基本相同,进行van der Pauw变温霍尔效应测试,采用镶嵌结构模型用Srikant方法和W-H方法拟合,再进行霍尔迁移率曲线拟合,分析两类测试拟合得到的位错密度.

图1是镶嵌块(马赛克结构)模型,其中图1(a)表示外延膜内各晶粒(001)面杂乱无章地偏离生长面法线,存在所谓平均倾转角βtilt,图1(b)表示各晶粒横向发生了扭转,存在所谓平均扭转角βtwist.Srikant方法采用对样品系列晶面(如(105),(104),···,(201)等)的ω摇摆曲线进行Pseudo-Voigt函数拟合,得到各晶面的FWHM,再根据旋转刚体模型对FWHM拟合,得到βtilt和βtwist,即FWHM-ω图线中倾斜角ψ=0°和ψ=90°时的FWHM值;而W-H方法认为对称衍射面(002),(004),(006)ω摇摆曲线的FWHM由晶粒尺寸效应加宽和平均倾转角βtilt加宽所致,即[13]

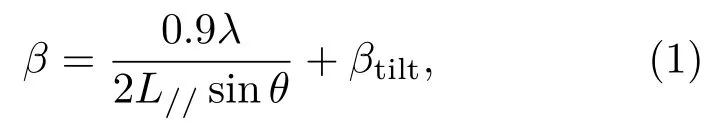
其中λ,L//,θ分别为X射线波长、面内共格长度、布拉格角. 以衍射矢量q(=2sinθ/λ)为横轴,β(=FWHM)沿qx方向的分量Δqx(=FWHM·2sinθ/λ)为纵轴,(1)式变形为

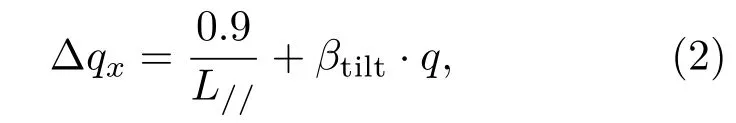
作Δqx随q变化的图线,直线斜率k=βtilt,截距y0=0.9/L//.两模型里刃、螺位错密度分别为其中be=0.3189 nm,bs=0.5185 nm.

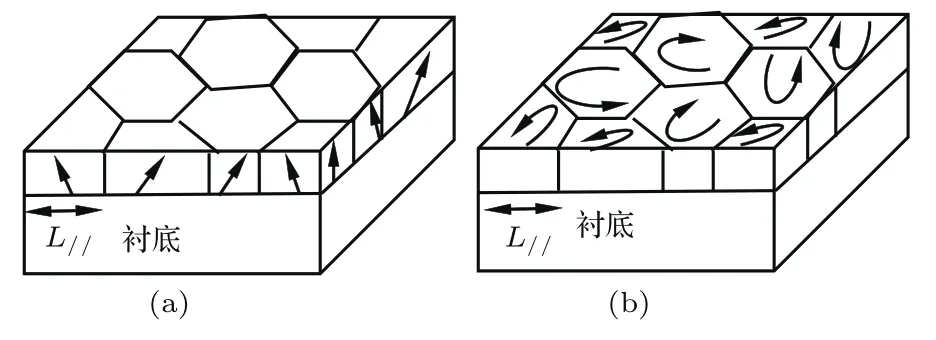
图1 镶嵌块(马赛克结构)中的面内共格长度L// (a)倾转βtilt;(b)扭转βtwistFig.1.Illustrations of a mosaic layer structure with the lateral coherence length,tilt in(a)and twist in(b).

而莫特相变材料(Mott transition,载流子浓度高于1018cm−3)和非莫特相变材料(载流子浓度低于1018cm−3)的霍尔迁移率分别为[14,15]

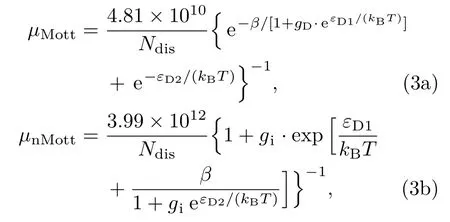
其中简并因子gD=gi=2,位错密度Ndis、刃螺位错密度比β、刃位错周围浅施主电离能εD1、螺位错周围浅施主电离能εD2为拟合参数.位错密度、迁移率分别以cm−2,cm2/(V·s)为单位,螺位错、刃位错密度为

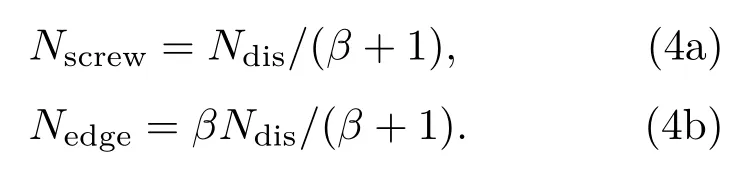
2.2 实 验

高分辨TAXRD采用PANalytical公司X’Pert Pro MRD型X射线衍射仪,对氢化物气相外延(HVPE)方法生长的59#(掺Si)、60#(非故意掺杂)样品以及金属有机物化学气相沉积(MOCVD)方法生长的12#掺Si样品的多个非对称衍射面进行了斜对称ω扫描,(002),(004),(006)衍射面进行对称ω扫描.表1为对摇摆曲线进行Pseudo-Voigt函数拟合得到的FWHM值,由表1可见,59#,60#两样品各晶面的FWHM值非常接近.

van der Pauw变温霍尔效应测试采用ECOPIA公司的 HMS-5000/HMS-5500全自动变温霍尔效应测试仪.测试电流为1 mA,磁场为5.5 kG,温控精度0.5 K,样品尺寸10 mm×10 mm,铟做电极,测试范围为80(100)—520 K.需要指出的是,59#样品数次欧姆接触都未做好,后来采用北方微电子公司的ELEDETM380G(P)型高密度等离子ICP(感应耦合等离子)刻蚀机做了表面Ar气处理才得以成功,ICP在EPD方法测试n-GaN材料位错密度的实验中,是常用技术[11].

表1 59#,60#,12#样品多个晶面ω扫描的FWHM(单位:(°))Table 1. ω-FWHM of re flections of sample 59#,60#,12#(unit:(°)).

3 结果与讨论

图2所示为59#,60#两样品采用Srikant方法[6]拟合的效果图,其中对于59#掺Si样品,βtilt=0.07092°,βtwist=0.10258°; 对于60#非故意掺杂样品,βtilt=0.06523°,βtwist=0.09859°,换算得到的刃、螺位错密度也非常接近.

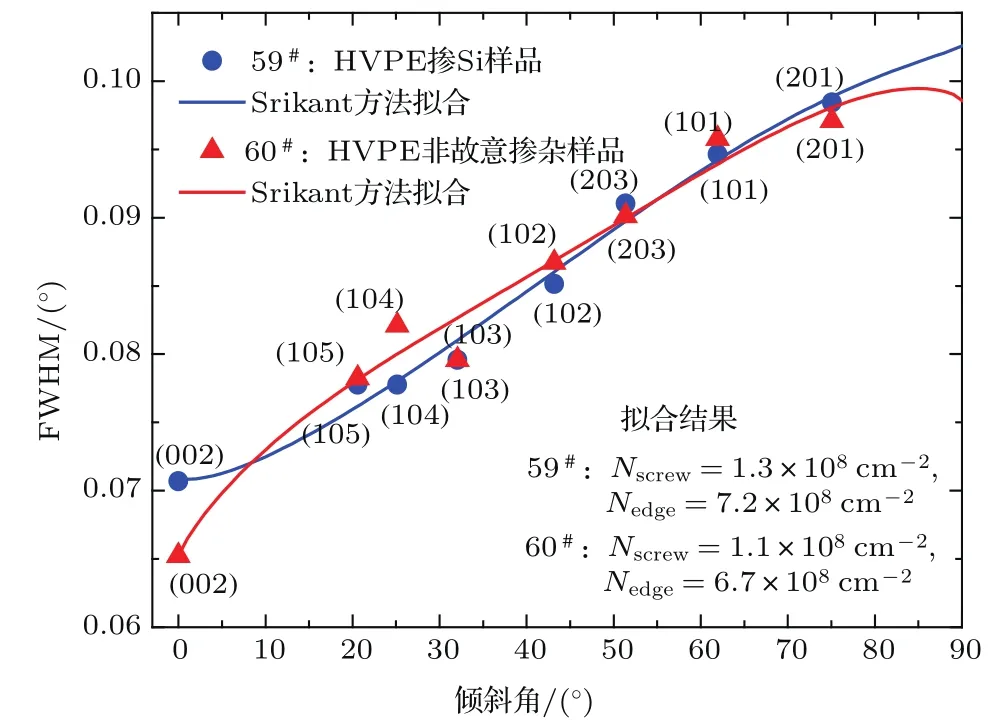
图2 (网刊彩色)59#,60#样品各晶面ω扫描摇摆曲线FWHM与倾斜角ψ的关系Fig.2.(color online)Width of ω-scans as a function of inclination angle ψ for sample 59#and 60#grown by HVPE.The symbols are experimental data and the lines are fi ts to them by using Srikant model.

然而,59#,60#样品的van der Pauw变温霍尔效应测试结果却大相径庭,如图3所示.59#样品室温载流子浓度和霍尔迁移率分别为nH=1.96×1017cm−3,µH=179 cm2/(V·s),而60#样品室温载流子浓度和霍尔迁移率分别为nH=5.47×1018cm−3,µH=199 cm2/(V·s),分别属于非莫特相变材料和莫特相变材料,前者螺位错、刃位错、总位错密度分别约为后者的2倍、3倍、3倍,如表2所列.为揭示其中的缘由,我们将两样品做了(002),(004),(006)面的对称衍射ω扫描,进行W-H方法测试,测试结果如图4所示.

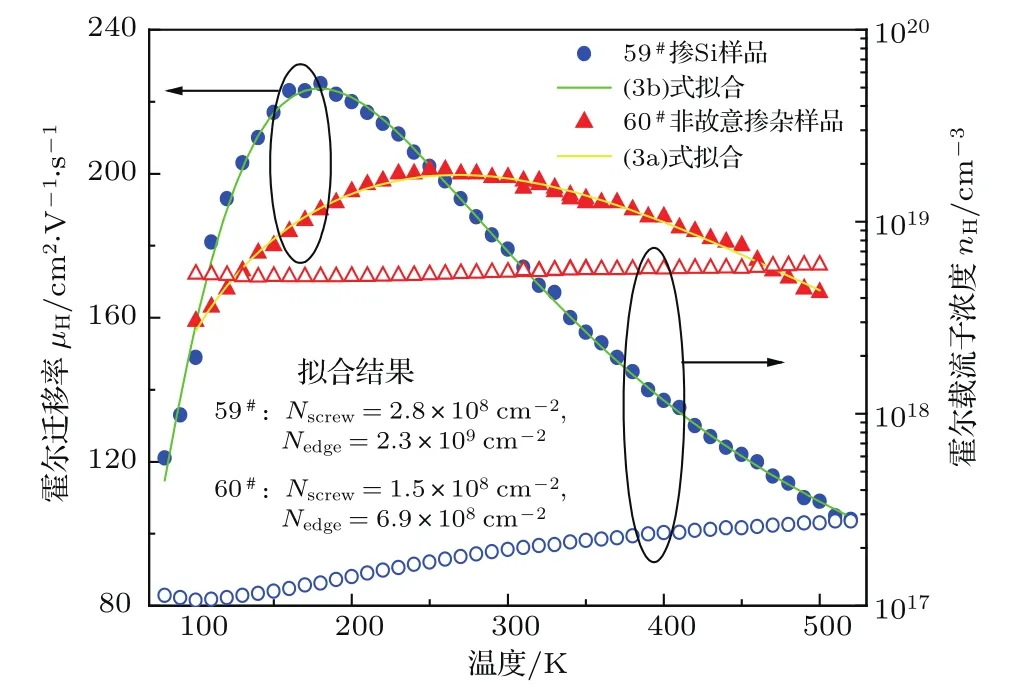
图3 (网刊彩色)对59#,60#样品霍尔迁移率的拟合Fig.3. (color online)Experimental(points)and model(solid lines)mobility for sample 59#and 60#;the latter is determined by a least-square fi t to mobility model through using Eq.(3b)and(3a),respectively.

表2 样品59#,60#,12#分别采用Srikant方法、W-H方法与迁移率拟合方法获得的测试结果的比较Table 2.The comparison of dislocation densities of sample 59#,60#and 12#determinated from the fitting methods including the Srikant,W-H and mobility,respectively(unit:108cm−2).

图4中59#样品的截距虽然比60#只大一点点,但其晶粒大小(即面内共格长度L//)为796 nm,约为60#样品(1517 nm)的一半,可见前者的晶界区域要大得多,TAXRD技术大大低估了59#样品的位错密度,问题就出在这晶界区域.因为晶界区域晶格严重畸变,晶面间距发生了很大变化,而ω扫描测试的是晶面间距相同的晶粒的取向差,换句话说,TAXRD技术对晶界区域是盲区,大量位错被“隐藏”了.进一步的解释是,对完美单晶,当单色器、样品和分析器都调到各自衍射面的布拉格角时,产生布拉格衍射,样品转动时,即偏离其布拉格衍射角,探测器接收到的强度将迅速下降.当样品由晶面间距相同但取向不同的晶粒(即嵌镶块或马赛克结构)组成时,样品转动后,虽偏离了样品中某个区域的布拉格衍射,但可能满足另外一个晶面间距相同而取向不同的晶粒的布拉格衍射,从而使得样品在转动过程中,不同取向的晶格先后满足其衍射条件,造成衍射峰宽化.晶粒中位错越多,则取向偏离越大,布拉格衍射的位置也越多,ω摇摆曲线越宽,FWHM越大;但当有位错在晶界里,由于晶界区域晶格畸变程度不一样,晶面间距就不一样,布拉格角也不一样,无法形成干涉,分析器就接受不到来自晶界处的衍射信息,难以检测到该处的位错.

为验证以上分析,我们挑选MOCVD方法生长的12#掺Si样品同样进行了TAXRD和van der Pauw变温霍尔效应测试,实验结果如图5和图6所示.图5中,随着晶面倾斜角ψ增大,FWHM无规则地逐渐减小,这种结果尚未见文献报道.由图4中W-H方法计算得知,该样品平均晶粒大小只有L//=171 nm,这么小的晶粒,使整个晶体几乎都是晶格畸变区域,而迁移率拟合表明总位错密度Ndis=8.4×108cm−2,由此可知平均位错线间距d=335 nm,因此晶粒中不应有位错,位错全在XRD的“盲区(晶界)”里.之所以倾斜角ψ越小FWHM越大,是因为12#样品厚度达到7.73µm,晶面弯曲严重.实验表明[16],晶面翘曲加宽效应规律是,基本不会加宽倾斜角ψ接近90°的晶面,且ψ越小的晶面摇摆曲线加宽越大.因此,FWHM随ψ增大而减小,表明对位错而言,晶界晶格畸变区域确是TAXRD测试的“盲区”,59#样品晶界区域刃、螺位错没被TAXRD“计入”,因此FWHM大幅降低.

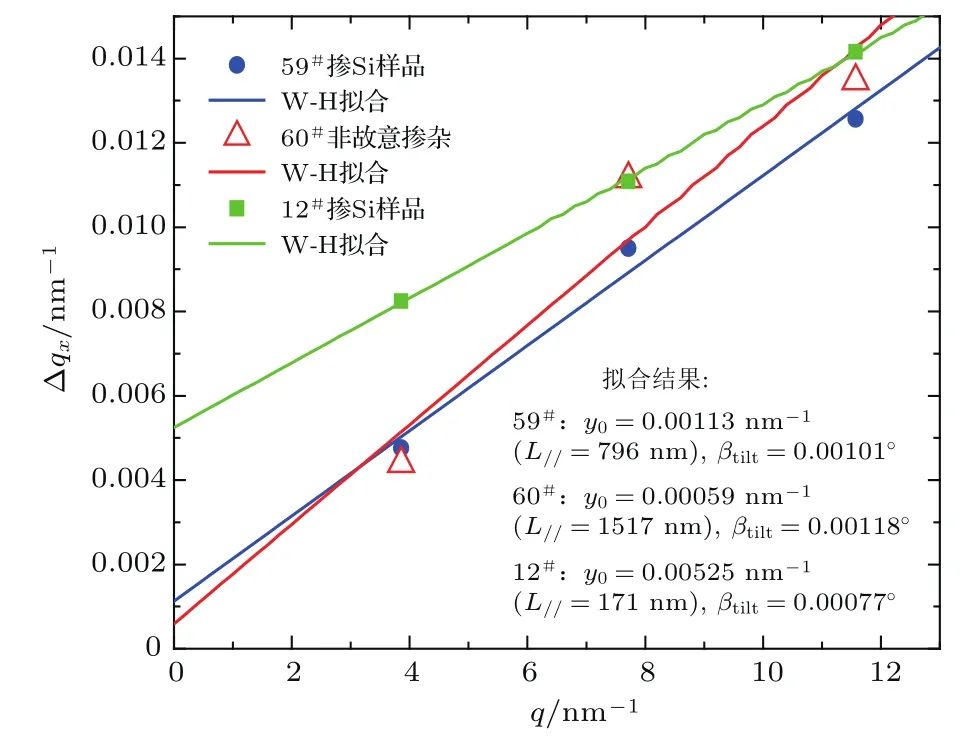
图4 (网刊彩色)59#,60#,12#样品各对称衍射面ω扫描W-H图Fig.4.(color online)W-H plot,Δqx(FWHM along qxdirection)versus q,for a series of symmetric refl ections for samples 59#( fi lled circle),60#(open triangle)and 12#( fi lled square).For the three samples,the mean mosaic tilt estimated from the fitting are 0.0579°,0.0676° and 0.0439°,respectively.The straight line is a fi t using Eq.(2).

60#样品的TAXRD测试结果略微小于电学测试值,表明晶界区域位错较少.这是因为晶粒大小(L//)为1.5µm,在三个样品中尺寸最大,晶界区域横截面积最小,相对位错也较少,对测量结果影响不大.结合三个样品情况,可以认为Srikant和W-H方法只适合检测晶粒大小(L//)在1.5µm以上翘曲不明显的材料.对大量样品霍尔迁移率拟合表明,非莫特相变材料的螺位错占总位错的10%以下,如果忽略晶界处的位错,则对应的扭转角与倾转角之比βtwist/βtilt大于2.0,因此,可用βtwist/βtilt≥2.0作为Srikant方法测试是否准确的依据,否则,需进一步由W-H方法确定L//≥1.5µm,才能确保测试的准确性.

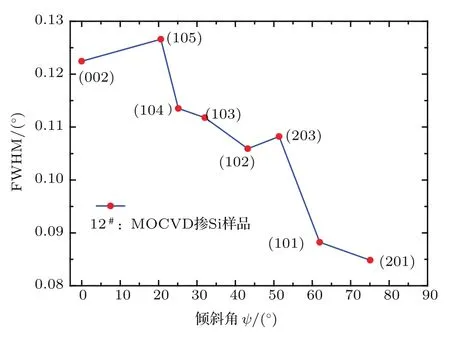
图5 (网刊彩色)12#样品各晶面ω扫描摇摆曲线FWHM与倾斜角ψ的关系Fig.5.(color online)Width of ω-scans as a function of inclination angle ψ for sample 12#grown by MOCVD.The symbols are experimental data and the lines are guides to the eye.

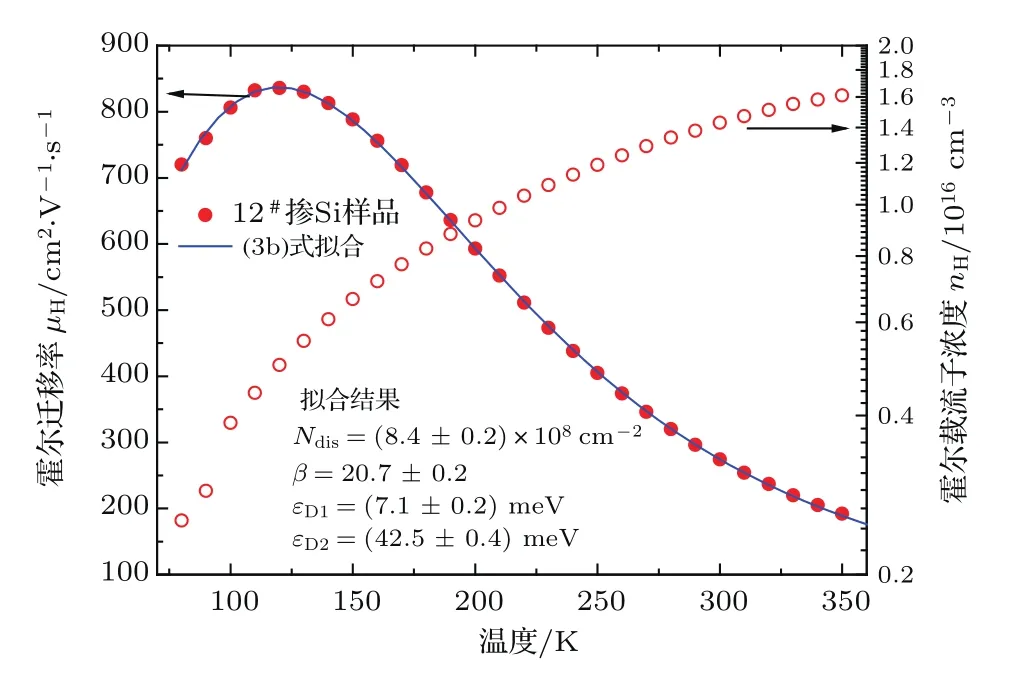
图6 (网刊彩色)对12#样品霍尔迁移率的拟合Fig.6. (color online)Experimental(points)and model(solid line)mobility for sample 12#grown by MOCVD;the latter is determined by a least-square fi t through using Eq.(3b).

最后需要指出的是,X射线双轴(晶)衍射在探测器前没有分析器,可以接收到样品各个方向散射的强度,导致ω-FWHM和位错密度偏大[13],但同样由于晶界处位错检测的盲点问题,可能存在严重的低估.

4 结 论

本文针对高分辨TAXRD和van der Pauw变温霍尔效应都是半导体材料方面的精确测量技术和主流测试方法,而在对纤锌矿n-GaN材料位错密度测量方面,前者常有较大误差,精确度远不及后者的实际情况,根据ω扫描测试的本质,采用了有特殊条件的实验和理论分析,指出了晶粒尺寸效应(晶界)、翘曲对FWHM 影响的变化规律,明确了前者准确测试的条件.分析表明,晶粒大小(L//)小于1.5µm的材料,晶界处可能存在大量位错,难以被高分辨TAXRD方法检测到,会使测试结果严重低估.计算表明,Srikant方法适用于扭转角与倾转角之比βtwist/βtilt≥2.0的样品,对于βtwist/βtilt＜2.0的样品,需由W-H方法确定L//≥1.5µm,才能确定测试的准确性.

感谢南昌大学国家硅基LED工程技术研究中心在实验测试方面提供的大力支持.

[1]Sugiura L 1997Appl.Phys.Lett.70 1317

[2]Li S,Fang Z,Chen H,Li J,Chen X,Yuan X 2006Mater.Sci.Semicond.Process.9 371

[3]Li D S,Chen H,Yu H B,Jia H Q,Huang Q,Zhou J M 2004J.Appl.Phys.96 1111

[4]Pomarico A A,Huang D,Dickinson J,Baski A A,Cingolani R,Morko H 2003Appl.Phys.Lett.82 1890

[5]Li C R,Mai Z H,Hatton P D,Du C H 1993Acta Phys.Sin.42 1479(in Chinese)[李超荣,麦振洪,Hatton P D,Du C H 1993物理学报42 1479]

[6]Srikant V,Speck J S,Clarke D R 1997J.Appl.Phys.82 4286

[7]Williamson G K,Hall W H 1953Acta Metall.1 22

[8]Metzger T,Hopler R,Born E,Ambacher O,Stutzmann M,Stommer R,Schuster M,Gobel H,Christiansen S,Albrecht M,Strunk H P 1998Philos.Mag.A77 1013

[9]Xie Z L,Zhou Y J,Song L H,Liu B,Hua X M,Xiu X Q,Zhang R,Zheng Y D 2010Sci.China:Phys.Mech.Astron.53 68

[10]Ivantsov V,Volkova A 2012ISRN Condens.Matter Phys.2012 184023

[11]Chierchia R,Böttcher T,Heinke H,Einfeldt S,Figge S,Hommel D 2003J.Appl.Phys.93 8918

[12]Pandey A,Yadav B S,Rao D V S,Kaur D,Kapoor A K 2016Appl.Phys.A122 614

[13]Safriuk N V,Stanchu G V,Kuchuk A V,Kladko V P,Belyaev A E,Machulin V F 2013Semicond.Phys.,Quantum Electron.Optoelectron.16 265

[14]He J S,Zhang M,Pan H Q,Zou J J,Qi W J,Li P 2017Acta Phys.Sin.66 067201(in Chinese)[何菊生,张萌,潘华清,邹继军,齐维靖,李平2017物理学报66 067201]

[15]He J S,Zhang M,Pan H Q,Qi W J,Li P 2016ActaPhys.Sin.65 167201(in Chinese)[何菊生,张萌,潘华清,齐维靖,李平2016物理学报65 167201]

[16]Moram M A,Vickers M E,Kappers M J,Humphreys C J 2008J.Appl.Phys.103 093528

PACS:61.72.Dd,61.72.Hh,73.43.Fj,81.70.Fy DOI:10.7498/aps.66.216102

*Project supported by the Natural Science Foundation of Jiangxi Province,China(Grant No.20151BAB207066)and the Natural Science Foundation of College of Science and Technology of Nanchang University,China(Grant No.2012-ZR-06).

†Corresponding author.E-mail:Hejusheng_2004@sohu.com

Analyses of determination conditions of n-GaN dislocation density by triple-axis X-ray di ff raction∗

He Ju-Sheng1)†Zhang Meng2)Zou Ji-Jun3)Pan Hua-Qing4)Qi Wei-Jing2)Li Ping5)

1)(School of Science and Technology,Nanchang University,Nanchang 330029,China)
2)(School of Material Science and Engineering,Nanchang University,Nanchang 330031,China)
3)(Engineering Research Center of Nuclear Technology Application(East China Institute of Technology),Ministry of Education,Nanchang 330013,China)
4)(Department of Mechanical Engineering,Shangrao Vocational and Technical College,Shangrao 334100,China)
5)(Modern Education Technology Center of Nanchang University,Nanchang 330031,China)

d 26 July 2017;revised manuscript

4 August 2017)

Dislocation densities of two hydride vapor phase epitaxy-grown hexagonal GaN samples,which are Si doped and unintentionally doped respectively,are determined by triple-axis X-ray diffractometry and van der Pauw variable temperature Hall-effect measurement.The dislocation densities of these two samples should be at the same level from the X-ray testing,theω-FWHM(full width at half maximum)values of all corresponding re flections for these two samples are almost the same.But from the Hall-effect measurements,the dislocation density values should be different from each other remarkably,because the unintentionally doped sample belongs to Mott transition material,while the Si-doped one does not.This fact indicates that the X-ray testing is perhaps inaccurate under some conditions,although the triple-axis X-ray diffractometry is a highly suitable technique for discriminating different kinds of structural defects such as edge and screw dislocations that lead to characteristic broadening of symmetric and asymmetric Bragg re flection.The experimental result obtained so far(say,for hot-electron bolometer)shows that the dislocation density value from mobility fitting model is in good accordance with that fromω-FWHM fitting using Srikant method.The anomaly that the dislocation density fromω-FWHM fitting is much lower than that from mobility fitting for the same sample(sample 59#),indicates that dislocations located in grain boundary may not be tested by triple-axis X-ray diffractometry.According to mosaic model,the layer is assumed to consist of single crystallites,called mosaic blocks,which are assumed to be slightly misoriented with respect to each other.The out-of-plane rotation of the block perpendicular to the surface normal is of the mosaic tilt,and the in-plane rotation around the surface normal is of the mosaic twist.The average absolute values of tilt and twist angles are directly related to the FWHM values of the corresponding distributions of crystallographic orientations.So,the X-ray testing can determine the average orientation of the grains with the same interplanar distance,excluding the information about the grain boundary at which X-ray cannot interfere because of disdortion of lattice.The experimental results and calculation analyses indicate that the dislocation density value from Srikant model is accurate when the ratio of twist angle to tilt angle exceeds 2.0,or the magnitude of the lateral coherence length is larger than 1.5µm.

gallium nitride,high-resolution triple-axis X-ray di ff raction,dislocation density,grain boundary

三轴X射线衍射技术广泛应用于半导体材料参数的精确测试,然而应用于纤锌矿n-GaN位错密度的测试却可能隐藏极大的误差.本文采用三轴X射线衍射技术测试了两个氢化物气相外延方法生长的n-GaN样品,发现两样品对应衍射面的半高全宽都基本一致,按照镶嵌结构模型,采用Srikant方法或Williamson-Hall方法,两样品的位错密度也应基本一致.但van der Pauw变温霍尔效应测试表明,其中的非故意掺杂样品是莫特相变材料,而掺Si样品则是非莫特相变材料,位错密度有数量级的差别.实验表明,位错沿晶界生长导致的晶粒尺寸效应,表现为三轴X射线衍射技术检测不到晶界晶格畸变区域的位错,给测试带来极大误差,这对正确使用Srikant方法和Williamson-Hall方法提出了测试要求.分析表明,当扭转角与倾转角之比βtwist/βtilt≥2.0时,Srikant方法是准确的,否则需进一步由Williamson-Hall方法确定晶粒大小(面内共格长度L//),当L//≥1.5µm时,Srikant方法是准确的.

10.7498/aps.66.216102

∗江西省自然科学基金(批准号:20151BAB207066)和南昌大学科学技术学院自然科学基金(批准号:2012-ZR-06)资助的课题.

†通信作者.E-mail:Hejusheng_2004@sohu.com

©2017中国物理学会Chinese Physical Society