基于时间序列符号化模式表征的有向加权复杂网络∗

曾明 王二红 赵明愿 孟庆浩

(天津大学电气自动化与信息工程学院,机器人与自主系统研究所,天津市过程检测与控制重点实验室,天津 300072)

基于时间序列符号化模式表征的有向加权复杂网络∗

曾明†王二红 赵明愿 孟庆浩

(天津大学电气自动化与信息工程学院,机器人与自主系统研究所,天津市过程检测与控制重点实验室,天津 300072)

(2017年5月19日收到;2017年7月3日收到修改稿)

有向加权复杂网络,时间序列分析,可视图建网,Logistic系统

1 引 言

复杂网络分析方法是把复杂系统内部基元之间的关系抽象为网络的节点和连边形式,然后通过量化分析网络的拓扑结构特性及动力学行为,揭示复杂系统的内在属性及运行规律等重要信息.复杂网络分析方法为不同类型的复杂系统(例如生物网络、脑神经网络、万维网、社交网络等)研究提供全新且形式统一的视角,因此受到了不同学科科研人员的广泛关注,并取得了一系列可喜的进展[1−7].

近些年来,研究人员进一步发现复杂网络方法也非常适用于挖掘理论模型难以精确描述的复杂(非线性)时间序列的内在重要信息[8−15].如何将时间序列映射为复杂网络(即复杂网络建网)是时间序列复杂网络分析系统中的关键环节.目前,经典的复杂网络建网方法有:基于伪周期时间序列划分的建网方法[14]、基于相空间重构建网方法[16−20]和可视图建网方法[9,21−23].2006年Zhang和Small[14]最早提出了将一维时间序列转换为复杂网络的概念,并在此基础上提出基于伪周期时间序列划分的建网方法,该方法首先将原始时间序列按照局部极小值(或极大值)划分为多个连续但不相交的周期子序列(这里的周期为伪周期,即每个周期长度近似相等),然后将每个周期定义为网络的一个节点,最后通过计算周期间的相关系数或相空间距离大小确定网络节点的连边,从而将时间序列映射为复杂网络.基于相空间重构建网方法是通过嵌入维数和延迟时间估算技术从原始时间序列中抽取一组多维向量作为复杂网络的节点,然后依据向量之间的相似性确定网络节点的连边,从而构造出原始时间序列对应的复杂网络,该方法在嵌入维数和延迟时间估算过程中存在不稳定因素,且连边关系判断的最佳阈值也很难确定,导致该方法应用的鲁棒性较差.可视图建网方法是将原始时间序列中的数据点作为网络的节点,数据点之间的可视关系作为网络的连边.相比相空间重构建网方法,可视图建网方法参数设置少、原理简单、易于编程实现.大量实验测试表明,上述建网方法粗分不同类型时间序列信号(如周期信号、随机信号、混沌信号、分形信号等)的结果较为满意,但在同一类型信号的精细分析方面存在明显不足.此外,以上两种方法的网络规模与原始时间序列的长度呈正相关关系,当时间序列长度过长,导致网络规模太大,普通计算机的计算能力无法满足要求.不仅如此,分析序列长度受限问题在多数复杂网络分析中普遍存在.

上面提到的建网方法构建的是无权、无向复杂网络.这类网络中各基元之间关系非常简单,如果有关联,两基元之间存在连边,否则不存在连边.但在很多实际复杂系统中,各基元之间的关联存在程度上的差异,因此不能简单地用“0”或“1”表示.此外,很多基元之间关联还存在方向性,例如基元A可以影响基元B,但基元B可能对基元A的状态没有影响,即基元A对基元B具有单向传递性.由此看出,无权、无向复杂网络无法精确反映网络节点(或基元)之间的关联程度及方向性差异,导致其在信号精细分析方面存在明显缺陷.在现实世界中经常会遇到一类复杂信号(如风场信号),这类信号的典型特点是其幅度呈现出跳跃式变化规律而非普通的渐变式变化.针对这类信号的特点,综合考虑信号基元的关联程度及方向性差异,本文提出了一种新的基于时间序列符号化结合滑窗技术模式表征的有向加权复杂网络建网方法.该方法首先依据跳变数据的等概率分布对时间序列进行符号化处理.然后利用滑窗技术获得有限个数的不同符号化模式确定网络的节点.最后通过计算符号化模式的转换频次确定网络权重,符号化模式的转换方向确定节点间的连接方向,最终建立时间序列有向加权复杂网络.

本文方法的优势主要体现在如下三方面:1)对复杂跳变数据进行符号化处理,可在保障分析精度的同时大大简化信号分析的复杂度;2)通过不同符号化模式的转换频次和方向确定网络权重和连接方向,更准确地反映复杂系统内部基元的关联程度和方向性;3)由于采用有限的符号化模式作为网络节点,因此本文方法受时间序列分析长度的影响小,可适用于大数据量时间序列分析.通过对经典Logistic信号和自然风场信号进行测试,验证了本文方法的可行性和先进性.

2 时间序列复杂网络建网方法

2.1 经典可视图复杂网络建网方法

可视图复杂网络建网方法是Lacasa等[21]在2008年提出的,时间序列以直方条的形式描绘到坐标轴上,直方条高度代表时间序列的数值大小(如图1(a)所示),该方法将时间序列的每个数据点映射成复杂网络中的节点,若两个直方条末端处相连,且并没有被其他直方条阻断,即两个节点可视,则这两个直方条所对应的网络节点有连边,通过对所有数据点做类似处理,从而确定各节点之间的网络连接关系(见图1(b)).

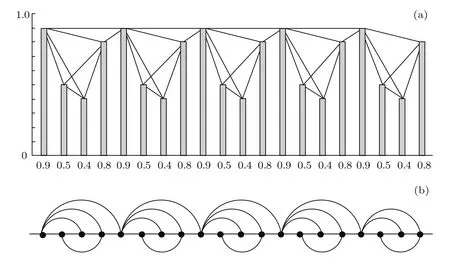
图1 时间序列可视图原理图[21]Fig.1.A time series and the associated graph derived from the visibility algorithm.

大量实验测试结果表明,可视图建网方法对不同类型的信号具有较好的区分能力,例如周期时间序列利用可视图建网方法将得到规则网络;随机序列可映射为随机网络;分形时间序列可映射为无标度网络.

2.2 基于符号化模式表征的有向加权复杂网络建网方法

本文提出的新方法主要针对一类呈现跳跃式变化的复杂时间序列信号(例如自然风场信号)进行建网分析.由于信号具有跳跃式变化特点,所以进行多区域分段划分处理可保障对原始信号精度损失较小的前提下大大简化分析信号的难度.为此,本文提出基于等概率符号化[24,25]结合滑窗技术模式表征的有向加权复杂网络建网方法.该方法首先将原始时间序列进行Z标准化处理,处理后的时间序列满足均值为0,方差为1的标准正态分布.然后,将其等概率划分成若干区间,不同区间用不同的字符来表示,实现时间序列的符号化转换.采用(3)式可将原始时间序列{xh,h=1,2,···,n}进行标准化处理,得到新的标准化时间序列{yh,h=1,2,···,n}:

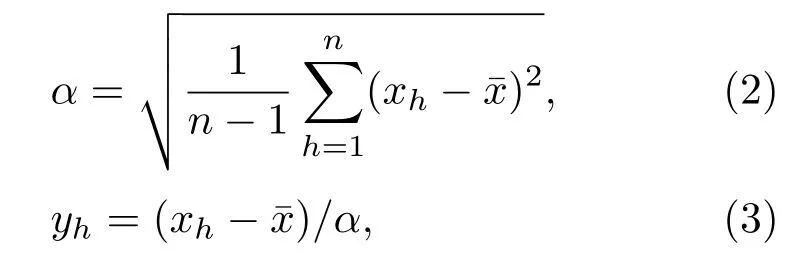
其中,n为时间序列长度,是原始时间序列的均值,α为原始时间序列的标准差.根据等概率区间划分的原则,确定每一个区间划分点,然后将落在每个区间的数值用一个字母符号表示,最后可得到符号化序列

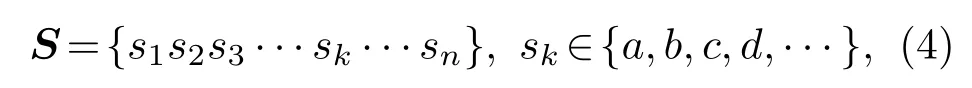
其中,a,b,c,d等为字母符号,如图2所示.从图2可以看出,符号化序列较好地保留了原始序列的跳变状态.下一步设置一个固定长度为l(默认值为4)的滑窗,从符号化序列S的第一个符号开始,自左向右滑动,这样就得到一系列长度为l的符号化子片段,实现对原始时间序列的符号化模式表征.

最后,将长度为l的不同符号化模式作为复杂网络的节点,模式之间的转换频次和转换方向确定网络节点之间连边的权重和方向.如果当前模式到下一时刻的模式发了变化,那么这两个模式之间存在连边且连接权重加1,连接方向为从当前模式指向下一个模式.如果当前模式与下一时刻模式相同,网络不发生变化.这样,就可将原始时间序列映射为符号化模式表征的有向加权复杂网络.

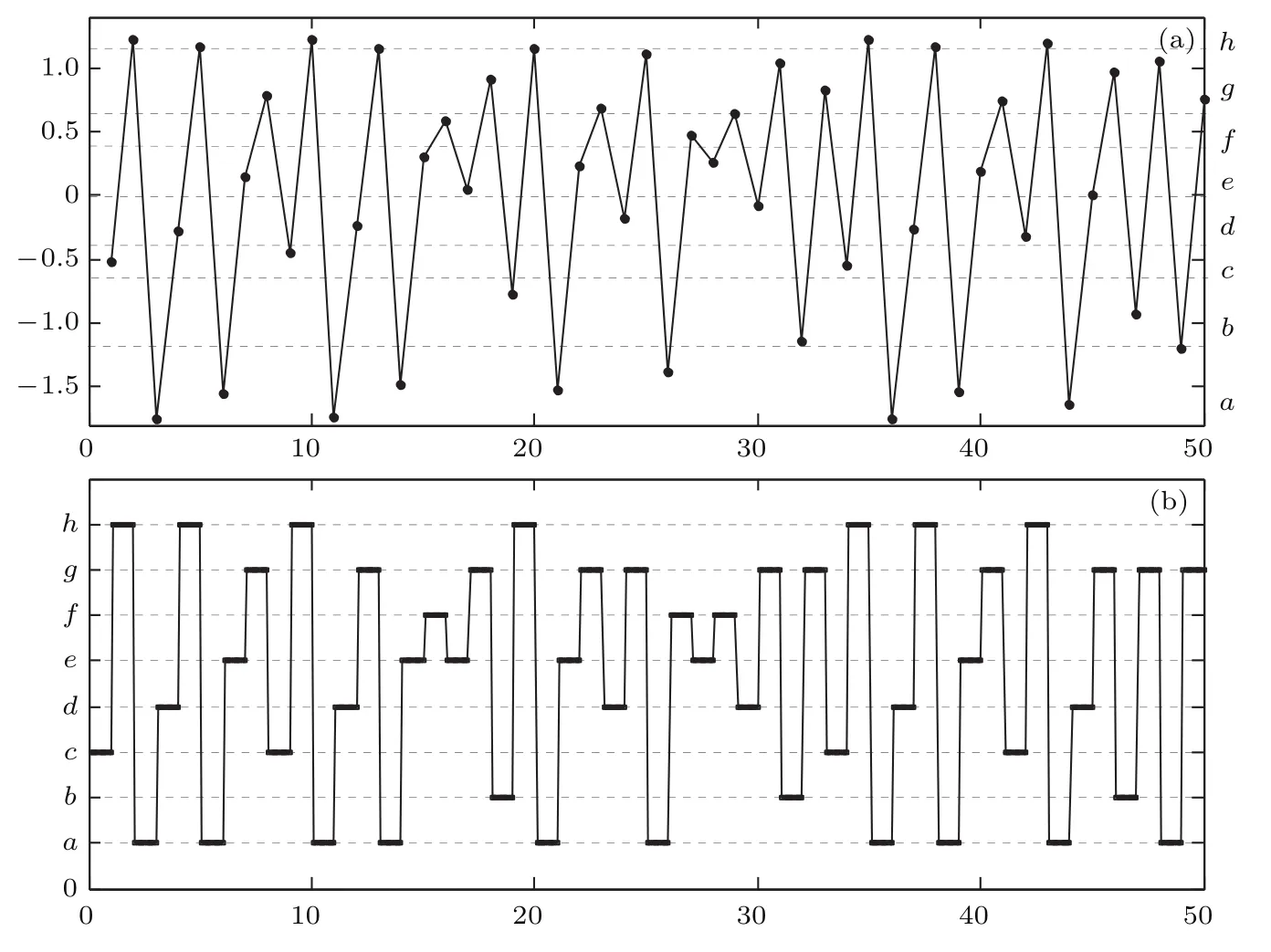
图2 时间序列符号化处理 (a)标准化时间序列;(b)符号化序列Fig.2.Time series symbolic process:(a)Standardized time series;(b)symbol series.

3 经典混沌信号的复杂网络分析实验

为了验证新型有向加权复杂网络的有效性和先进性,以Logistic映射系统在不同参数下的时间序列为例,分别采用经典可视图和本文提出的建网方法对具有不同拓扑结构的序列进行对比分析.

3.1 Logistic映射系统

Logistic映射系统是产生混沌时间序列的经典模型,它通过倍周期分叉进入混沌[26].Logistic映射系统模型方程如下:

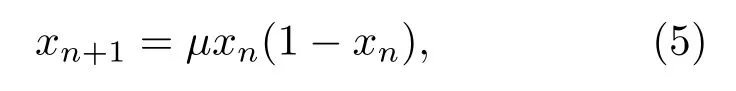
其中,µ为影响系统状态的主要参数,参数µ的不同取值对应不同的状态.

本文设定Logistic系统的初始值为0.5,步长为0.01,时间为100 s.参数µ分别取3.5,3.6,3.628,3.7,3.74,3.8,3.83,3.9,3.99这9个值时,可以得到不同的周期态和混沌状态的时间序列(见表1和图3).为了更清晰地显示波动状态,图3只绘制了每个时间序列前200个数据点.

表1 Logistic映射系统在不同参数下的状态Table 1.The state of Logistic system with different parameters.

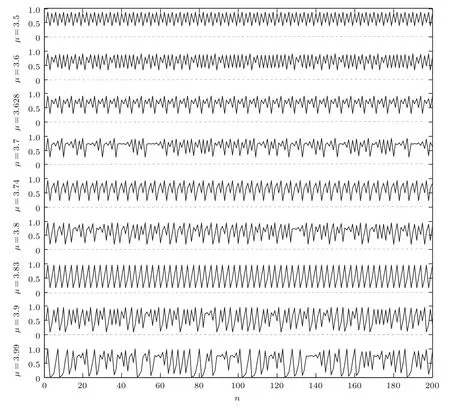
图3 Logistic系统在不同参数下的时间序列Fig.3.Time series of Logistic system with different parameters.

3.2 不同建网方法性能测试

3.2.1 可视图建网方法的测试结果

将9个不同参数下对应的Logistic系统时间序列分别进行建网分析.采用UCINET中的NETDRAW工具实现网络结构图的可视化.由于该软件无法实现大量数据量的可视化,因此仅给出前1000个数据点可视图建网的网络结构图(见图4).从图4可以看出,当参数µ为3.5,3.628,3.74,3.83时(系统为周期态),网络拓扑结构存在一定的差异,但结构差异与系统的解集数之间没有直接的关联.而参数µ取值为3.6,3.7,3.8,3.9,3.99时(系统为混沌态),其网络拓扑结构差异较小,都呈现出相似的簇团结构,无法区分系统不同的混沌强度差异.总体来看,可视图建网方法大致能区分周期态和混沌态,但对系统的细节差异区分度不明显.

3.2.2 新型有向加权复杂网络构建

依照2.2节中描述的建网步骤,将数据长度均为10000的不同状态Logistic时间序列映射为相应的有向加权复杂网络,其中滑窗长度l默认值为4.当符号化级数取值较小时,信号的失真较大,而当符号化级数取值较大时,可能的符号化模式数量会急剧增大,影响网络的分析效率.折衷考虑信号分析的复杂度和精度,我们通过大量测试,最终确定优选的符号化级数为12.图5给出了符号化级数为12时不同状态的Logistic时间序列映射的网络拓扑结构.

表1给出了Logistic映射系统在不同参数下的状态列表.从表1可以看出,当参数µ为3.5,3.628,3.74,3.83时,对应的时间序列为解集数固定的周期变化序列,解集数分别为4,6,5,3,这与图5给出的时间序列对应的复杂网络的规模(节点数)完全一致.当参数µ取值为3.6,3.7,3.8,3.9,3.99时,对应的时间序列为混沌强度递增时间序列,图5中对应的复杂网络规模也同样呈现出逐渐递增的趋势.由此可以看出,本文提出的有向加权复杂网络的拓扑结构不仅能直观地区分周期信号和混沌信号,且对周期序列和混沌序列的细微变化具有较好的敏感性.此外,图5显示虽然分析数据长度为10000,但相应的网络规模却不大(最多为140),由此可以看出,本文方法在处理大数据方面明显优于传统的可视图和相空间重构等建网方法.

图4 Logistic映射可视网络拓扑图Fig.4.The topological structures of Logistic map from the visibility graph network.

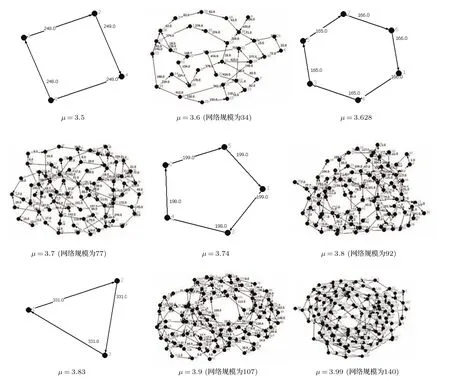
图5 Logistic系统有向加权复杂网络拓扑图Fig.5.The topological structures of Logistic system from the directed weighted complex network.

4 自然风场信号的复杂网络分析实验

4.1 自然风场数据获取

本实验主要目的是测试所构建的复杂网络对时间序列信号的量化分析能力,即网络特性指标的分析性能.为此,采集了一组具有特定空间位置关系的自然风场信号.九个二维超声波风速仪(WindSonic,Gill公司)相邻间隔为1 m排成一列(如图6所示),距地面高度为0.6 m,数据采集时间为1 h,采样频率为4 Hz.测得的风速时间序列如图7所示,各风速时间序列的均值如表2所列.

图6 风速仪空间排布示意图Fig.6.Deployment of nine two-dimensional ultrasonic anemometers.

图7 九个二维风速仪采集的风速时间序列Fig.7.Wind speed time series of nine two-dimensional ultrasonic anemometers.

表2 九个风速时间序列的均值Table 2.The means of nine wind speed time series.

4.2 风场信号的网络特性分析

利用本文提出的方法,将实验采集到的风速时间序列映射成有向加权复杂网络.下面选用加权聚类系数[27]和平均路径长度[28]两个网络特性指标量化地分析或挖掘时间序列的内在规律.

加权网络的聚类系数[27]由于具有连边权重的非均匀化特性,在衡量网络相邻节点之间的聚集度时,需考虑节点之间相关强度的影响.计算加权网络的节点i的加权聚类系数

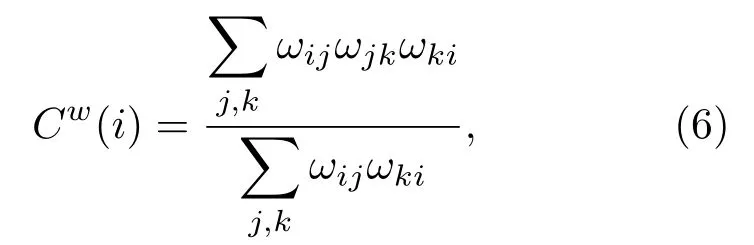
其中,ωij是从节点i到节点j连边的权重.从(6)式可以看出,网络中节点i的加权聚类系数越大,表明模式i与相邻模式之间存在规则且频繁的转换.网络的加权聚类系数WCC即为各个节点的加权聚类系数的均值,

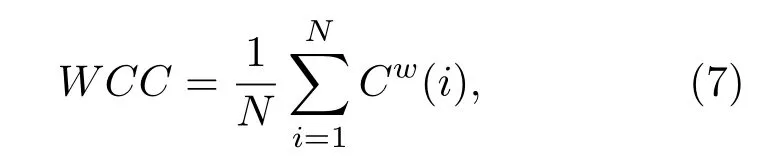
其中,N表示网络节点个数.加权聚类系数越大表明网络的连接越紧密、连接强度越高,但相比于无权网络,加权网络的聚类系数会明显较小.

有向加权网络中,两个节点i和j之间的加权最短路径dij[28]是指在从节点i到j的所有可能路径中最小的连边权重和,

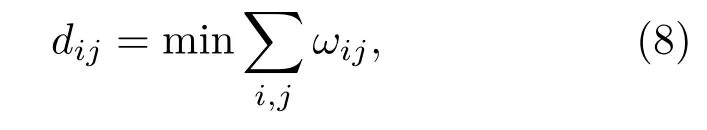
所以网络的平均路径长度L定义为

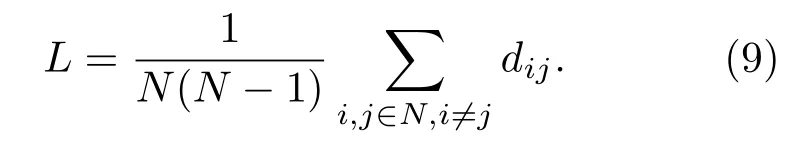
通过计算不同位置的风速时间序列有向加权网络的网络规模、加权聚类系数和平均路径长度这三个网络特性参数,分析这些参数与采集位置之间的关联性,并与可视图建网方法的网络特性指标做对比.

图8为不同位置风速信号可视图建网的网络特性分析结果,其中U1—U9代表顺序排列的9个风速仪位置.对于本文风速信号采集的实验环境,已有研究结果表明[29],虽然气态流场随时间不断变化,但在一定区域内(通常在10 m范围内)的风速/风向变化近似一致(如图7所示,9个风速时间序列大尺度波动基本一致,但在小尺度波动上存在一定的差异),且采集点距离越近波动的相似性越高.从图8可以看出,可视图建网的网络特性呈现无规律跳变,以聚类系数网络参数为例,风速仪U1与U5相距4 m,其相应聚类系数值大小相当,而与U1相距1 m的U2,其相应聚类系数值差别较大,这显然是不合理的,即网络特性大小与风速仪空间位置没有直接的关联.图9为本文提出的有向加权网络的网络特性分析结果.三个网络特性参数(网络规模、加权聚类系数和平均路径长度)大小随着风速仪排布的空间位置变化呈现出一致的增长或衰减趋势,这与参考文献[29]测试结果符合.

下面对本文方法的三个网络特性参数(网络规模、加权聚类系数和平均路径长度)分析得到的一致增长或衰减结果做进一步的说明.从9个采集点风玫瑰图统计结果显示,测试实验的主风向为东北方向,随着风的流动方向能量逐渐减弱(如表2所列),即风速仪U9采集的风速时间序列平均风速最大,自东向西逐渐减小(U2位置例外).参考文献[29]的研究结果表明,在小的局部空间范围内(通常小于10 m)平均风速越大,气流的随机波动幅度和频率都会越弱,即波动的复杂性越小.从图7给出的数据直观来看,U9和U1两个序列的大尺度波动基本一致,但U9序列(平均风速最大)的小尺度波动明显比U1序列(平均风速最小)弱,因此U9序列的复杂度比U1序列小.网络规模参数的大小反映时间序列中符号化模式的多少,符号化模式越多在一定程度上说明时间序列越复杂.U1序列由于波动的复杂度最大,因此网络规模值最大,其他位置U3—U9由于复杂度逐渐减小,所以网络规模值出现一致衰减的趋势.U2位置由于平均风速异常地变大,其网络规模值出现异常也是合理的.另外两个特性参数:加权聚类系数和平均路径长度也准确地反映了采集风速信号的复杂性差异,即信号的复杂度降低导致网络的符号化模式减少,同时模式之间的转换频次增加,使得网络的聚集度和平均路径长度增大,因此U1—U9序列的上述两个网络特性参数呈现出一致增长的趋势.上述分析表明,三个特性参数均能准确反映分析信号的相似性及复杂性差异.

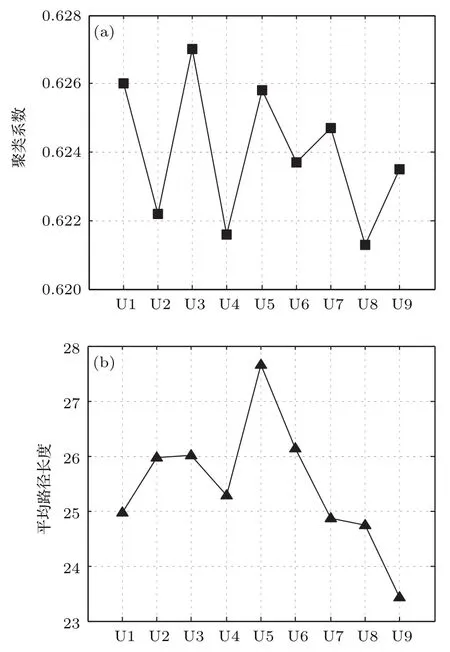
图8 风速时间序列的可视图网络特性 (a)聚类系数;(b)平均路径长度Fig.8.The visibility graph network characteristics of the wind speed time series:(a)Clustering coefficient;(b)average path length.

在电力系统中风能的预测、气象学中风场分区等应用中,经常要对不同空间位置采集的风场信号进行相似性及复杂性分析.由于自然风场信号是一类复杂的非线性非平稳信号,因此其相似性及复杂性准确度量至今没有有效的解决方案.本文提出的有向加权网络特性分析的方法为该难题的解决提供了一种有效的工具.此外,后续还可以在新的复杂网络基础上挖掘更丰富的网络拓扑结构信息,提出新的网络特性指标更深层次地揭示物理对象(如风场)的动力学机理.

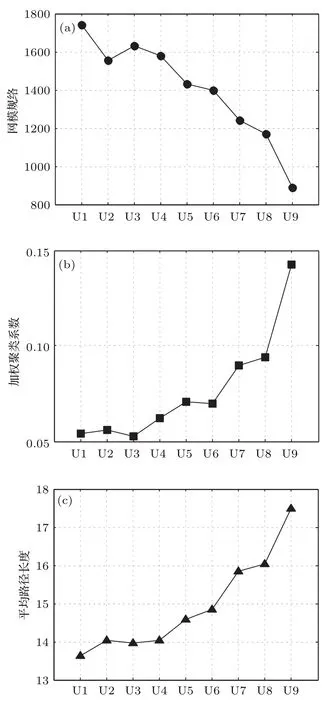
图9 风速时间序列的有向加权网络特性 (a)网络规模;(b)加权聚类系数;(c)平均路径长度Fig.9.The directed weighted network characteristics of the wind speed time series:(a)Network scale;(b)weighted clustering coefficient;(c)average path length.

5 结 论

本文提出了一种新的基于时间序列符号化结合滑窗技术模式表征的有向加权复杂网络建网方法.首先对标准化后的时间序列幅度进行等概率量化处理,将原始时间序列转化为更简洁的符号化序列;然后结合滑窗技术提取出一系列符号化模式作为复杂网络节点;最后将符号化模式的转换方向和转换频次作为连边方向和权重,从而构建出有向加权复杂网络.通过对不同参数条件下的Logistic映射系统的时间序列分析表明,本文提出的有向加权复杂网络的拓扑结构不仅能直观地区分周期信号和混沌信号,且能准确地反映周期时间序列和混沌时间序列的细微变化.另外,通过多点规则排列采集的风速信号的网络特性指标分析表明,本文方法的网络参数大小能较准确地预测风速仪的空间位置邻近关系.上述网络指标的量化分析结果,进一步证实了本文提出的方法相比经典的可视图方法,对于分析复杂的时间序列具有更高的灵敏度和准确性.

时间序列复杂网络分析包含两个研究分支:一是研究时间序列复杂网络建网方法;二是在建网基础上挖掘丰富的网络特性指标.本文的研究侧重点是构建新的时间序列复杂网络建网方法,后续可以在此基础上探寻具有普适性的有向加权网络的新的特性指标或针对特定研究对象设计新的特异性指标.另外,除进一步完善复杂网络分析方法外,后续还可以做大量涉及时间序列分析的推广应用研究.例如本文的风场实验证实了新提出的有向加权复杂网络的拓扑结构特征是一种非常有效的风场信号特征提取策略,未来在风能预测、风场模式分类、风场动力学及演化机理等研究中将有广阔的应用前景.

[1]Watts D J,Strogatz S H 1998Nature393 440

[2]Barabasi A L,Albert R 1999Science286 509

[3]Albert R,Barabási A L 2002Rev.Mod.Phys.74 47

[4]Buldyrev S V,Parshani R,Paul G,Stanley H E,Havlin S 2010Nature464 1025

[5]Rubinov M,Sporns O 2010Neuroimage52 1059

[6]Zhuang E,Small M,Feng G 2014Physica A410 483

[7]Hao X,An H,Qi H,Gao X 2016Appl.Energy162 2016

[8]Zhou L,Gong Z Q,Zhi R,Feng G L 2008Acta Phys.Sin.57 7380(in Chinese)[周磊,龚志强,支蓉,封国林2008物理学报57 7380]

[9]Lacasa L,Toral R 2010Phys.Rev.E82 036120

[10]Xu X,Zhang J,Small M 2008Proc.Natl.Acad.Sci.USA105 19601

[11]Donges J F,Donner R V,Kurths J 2013Europhys.Lett.102 10004

[12]Zou Y,Small M,Liu Z 2014New J.Phys.16 013051

[13]Huang X,An H,Gao X 2015Physica A428 493

[14]Zhang J,Small M 2006Phys.Rev.Lett.96 238701

[15]Gao Z K,Fang P C,Ding M S,Jin N D 2015Exp.Therm.Fluid Sci.60 157

[16]Takens F 1981Dynamical Systems and Turbulence,Warwick 1980898 366

[17]Yang Y,Yang H 2008Physica A387 1381

[18]Gao Z,Jin N 2009Chaos19 033137

[19]Tang J,Liu F,Zhang W,Zhang S,Wang Y 2016Physica A450 635

[20]Webber C L,Zbilut J P 1994J.Appl.Phys.76 965

[21]Lacasa L,Luque B,Ballesteros F,Luque J,Nuno J C 2008Proc.Natl.Acad.Sci.USA105 13

[22]Gao Z K,Hu L D,Zhou T T,Jin N D 2013Acta Phys.Sin.62 110507(in Chinese)[高忠科,胡沥丹,周婷婷,金宁德2013物理学报62 110507]

[23]Liu C,Zhou W X,Yuan W K 2010Physica A389 2675

[24]Lin J,Keogh E,Lonardi S,Chiu B 2003Proceedings of the 8th ACM SIGMOD workshop on Research Issues in Data Mining and Knowledge DiscoverySan Diego,USA,June 13,2003 p2

[25]Lin J,Keogh E,Li W,Lonardi S 2007Data Mining and Knowledge Discovery15 107

[26]Lü J H,Lu J A,Chen S H 2001Chaotic Time Series Analysis and Application(Wuhan:Wuhan University Press)p12(in Chinese)[吕金虎,陆君安,陈士华 2001混沌时间序列分析及其应用(武汉:武汉大学出版社)第12页]

[27]Shirazi A H,Jafari G R,Davoudi J,Peinke J,Tabar M R R,Sahimi M 2009J.Statist.Mech.:Theory and Experiment2009 P07046

[28]Antoniou I E,Tsompa E T 2008Discrete Dyn.Nat.Soc.2008 1

[29]Li J G,Meng Q H,Wang Y,Zeng M 2011Autonomous Robots30 281

PACS:05.45.Tp,88.50.jj,05.45.–a,89.75.–k DOI:10.7498/aps.66.210502

*Project supported by the National Natural Science Foundation of China(Grant Nos.61271321,61573253).

†Corresponding author.E-mail:zengming@tju.edu.cn

Directed weighted complex networks based on time series symbolic pattern representation∗

Zeng Ming†Wang Er-Hong Zhao Ming-Yuan Meng Qing-Hao

(Tianjin Key Laboratory of Process Measurement and Control,Institute of Robotics and Autonomous Systems,School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)

d 19 May 2017;revised manuscript

3 July 2017)

Complex networks are capable of modeling different kinds of complex systems in nature and technology,which contain a large number of components interacting with each other in a complicated manner.Quite recently,various approaches to analyzing time series by means of complex networks have been proposed,and their great potentials for uncovering valuable information embedded in time series,especially when nonlinear dynamical systems are incapable of being described by theoretical models have been proven.Despite the existing contributions,up to now,mapping time series into complex networks is still a challenging problem.In order to more effectively dig out the structural characteristics of time series(especially the nonlinear time series)and simplify the computational complexity of time series analysis,in this paper we present a novel method of constructing a directed weighted complex network based on time series symbolic pattern representation combined with sliding window technique.The proposed method firstly implements symbolic procession according to the equal probability segment division and then combines with the sliding window technique to determine the symbolic patterns at different times as nodes of the network.Next,the transition frequency and direction of symbolic patterns are set as the weights and directions of the network edges,thus establishing the directed weighted complex network of the analyzed time series.The results of test using the Logistic system with different parameter settings show that the topological structures of the directed weighted complex network can not only intuitively distinguish the periodic time series and chaotic time series,but also accurately re flect the subtle changes of two types of time series.These results are superior to those from the classical visibility graph method which can be only roughly classi fi ed as two types of signals.Finally,the proposed technique is used to investigate the natural wind field signals collected at an outdoor open space in which nine high precision two-dimensional(2D)ultrasonic anemometers are deployed in line with 1minterval.The topological parameters of the network analysis include the network size,weighted clustering coefficient,and average path length.The corresponding results of our approach indicate that the values of three network parameters show consistent increase or decrease trend with the spatial regular arrangement of the nine anemometers.While the results of the visibility graph network parameters are irregular,and cannot accurately predict the spatial deployment relationship of nine 2D ultrasonic anemometers.These interesting findings suggest that topological features of the directed weighted complex network are potentially valuable characteristics of wind signals,which will have broad applications in researches such as wind power prediction,wind pattern classi fication and wind field dynamic analysis.

directed weighted complex network,time series analysis,visibility graph,Logistic system

时间序列复杂网络分析近些年已发展成为非线性信号分析领域的一个国际热点课题.为了能更有效地挖掘时间序列(特别是非线性时间序列)中的结构特征,同时简化时间序列分析的复杂度,提出了一种新的基于时间序列符号化结合滑窗技术模式表征的有向加权复杂网络建网方法.该方法首先按照等概率区段划分的方式将时间序列做符号化处理,结合滑窗技术确定不同时刻的符号化模式作为网络的节点;然后将待分析时间序列符号化模式的转换频次和方向作为网络连边的权重和方向,从而建立时间序列有向加权复杂网络.通过对Logistic系统不同参数设置对应的时间序列复杂网络建网测试结果表明,相比经典的可视图建网方法,本文方法的网络拓扑能更简洁、直观地展示时间序列的结构特征.进而,将本文方法应用于规则排列采集的自然风场信号分析,其网络特性指标能较准确地预测采集信号的排布规律,而可视图建网方法的网络特性指标没有任何规律性的结果.

10.7498/aps.66.210502

∗国家自然科学基金(批准号:61271321,61573253)资助的课题.

†通信作者.E-mail:zengming@tju.edu.cn

©2017中国物理学会Chinese Physical Society